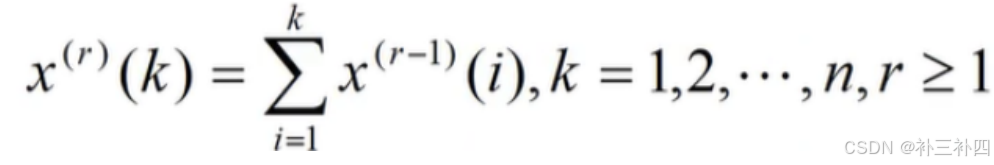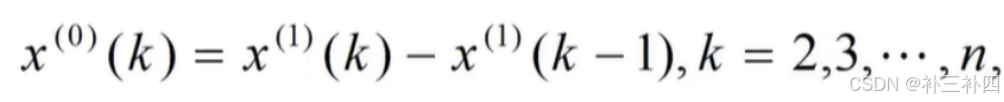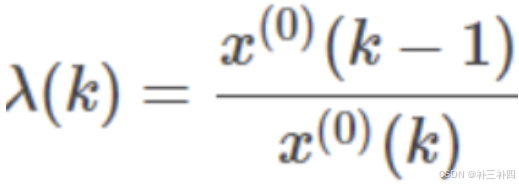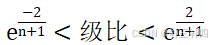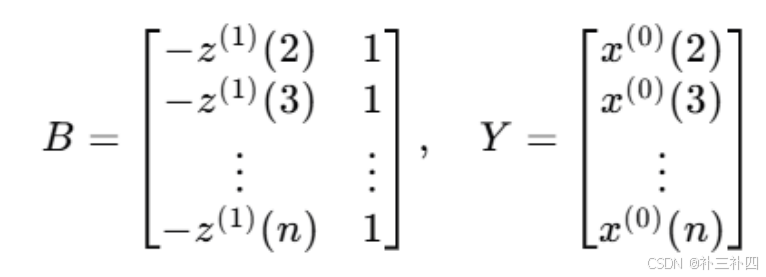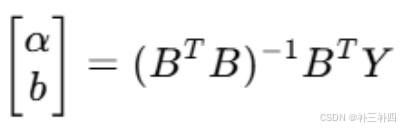特点:
利用少量、不完全的信息
预测的是指数型的数值
预测的是比较近的数据
灰色生成数列原理:
- 累加生成:
- 累减生成:通过累减生成还原成原始数列。
- 加权相邻生成:(会更接近每月中旬,更推荐用于缺失数据填补)
加权邻值生成的作用
平滑数据:通过加权邻值生成,可以减少数据的波动,使数据序列更加平滑,从而更好地反映数据的内在规律。
增强规律性:加权邻值生成可以增强数据的规律性,使数据序列更符合灰色预测模型的假设,从而提高模型的预测精度。
构造模型步骤:
检查数列的级比:
要求:
不符合则要对该序列进行平移处理
定义灰导数:
d(k)=x(0)(k)=x(1)(k)-x(1)(k-1)
利用邻值生成序列
Z(1)(k)=αx(1)(k)+(1-α)x(1)(k-1)
于是定义GM(1,1)的微分方程模型为:
X(0)(k)+αz(1)(k)=b
用回归分析
求得该解α和b
求解微分方程并得到预测值