前言：实现记忆化搜索的一般步骤 

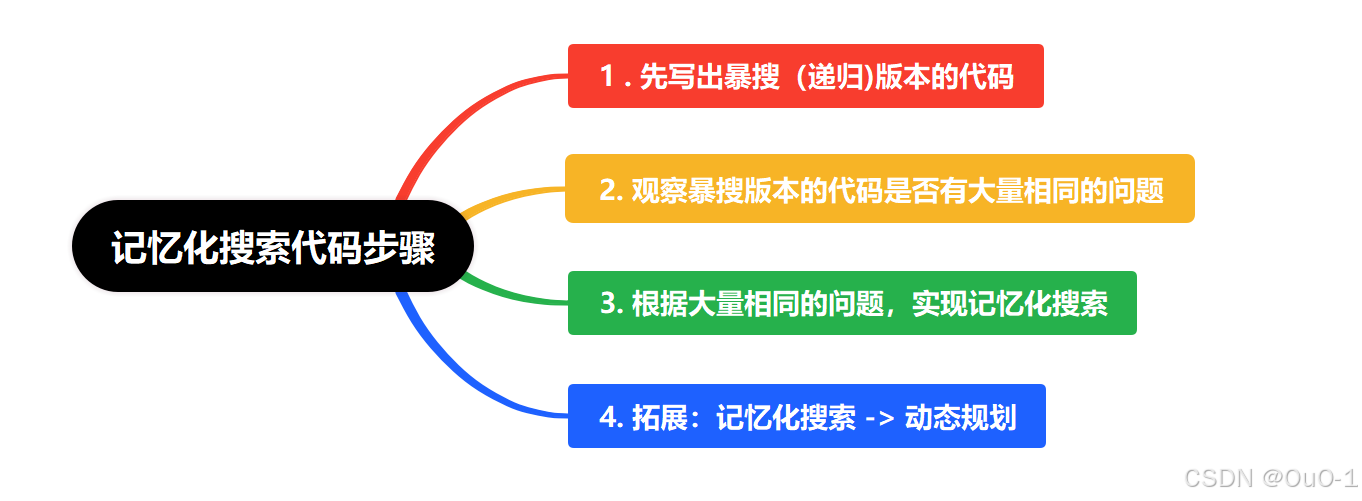
    (1) 实现记忆化搜索代码步骤    

---

---

    (2) 如何将暴搜代码转换成记忆化搜索代码?    

---

---

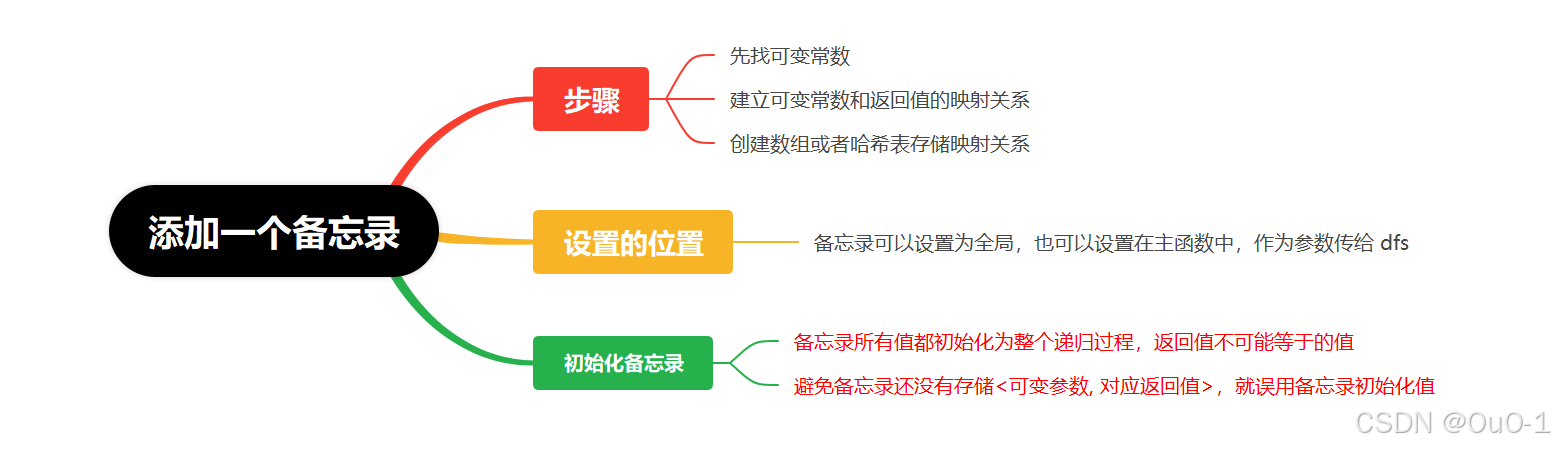
    (3）如何添加一个备忘录?        

---

斐波那契数

    题目解析    

    算法原理    

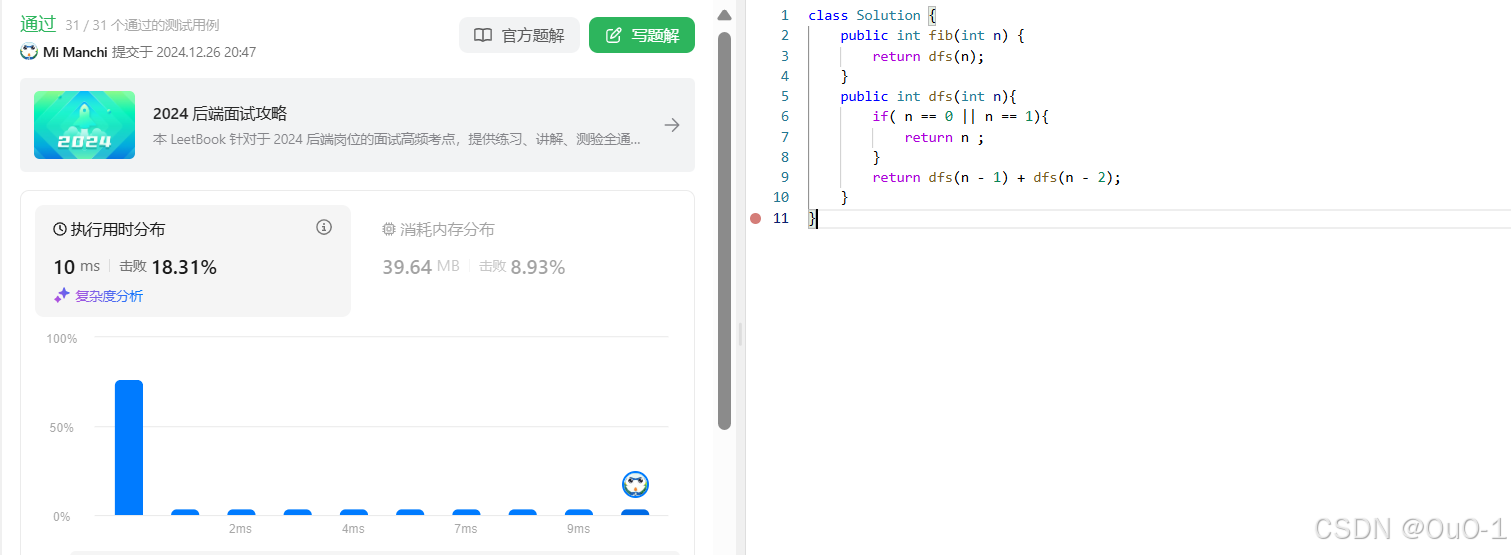
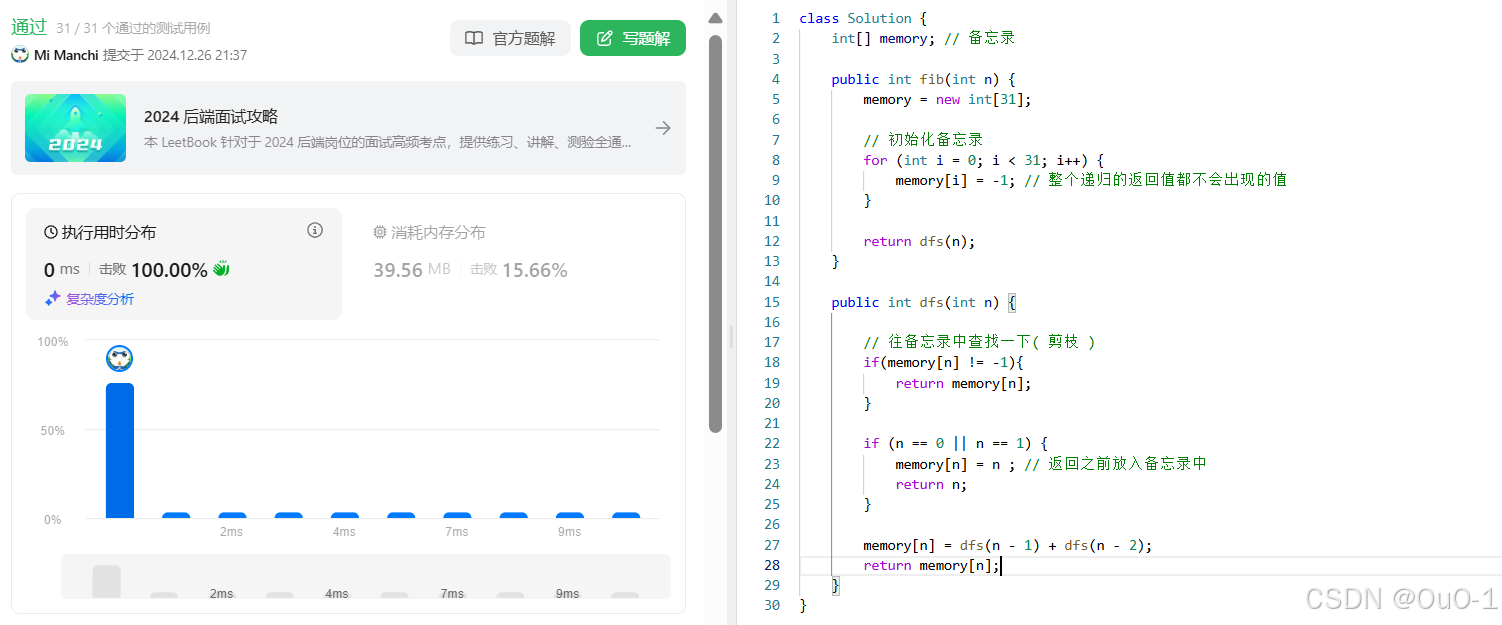
    解法一：递归      

 时间复杂度高是因为递归展开树有很多次重复计算，我们可以优化这些重复的计算；我们可以创建一个备忘录，当计算其中一个分支时，把计算出的 d(i) 放入一个"备忘录"中 ( i = 1 ....... n )，当递归其他分支时，我们通过备忘录存储好的计算结果，减少递归树额外重复的展开；

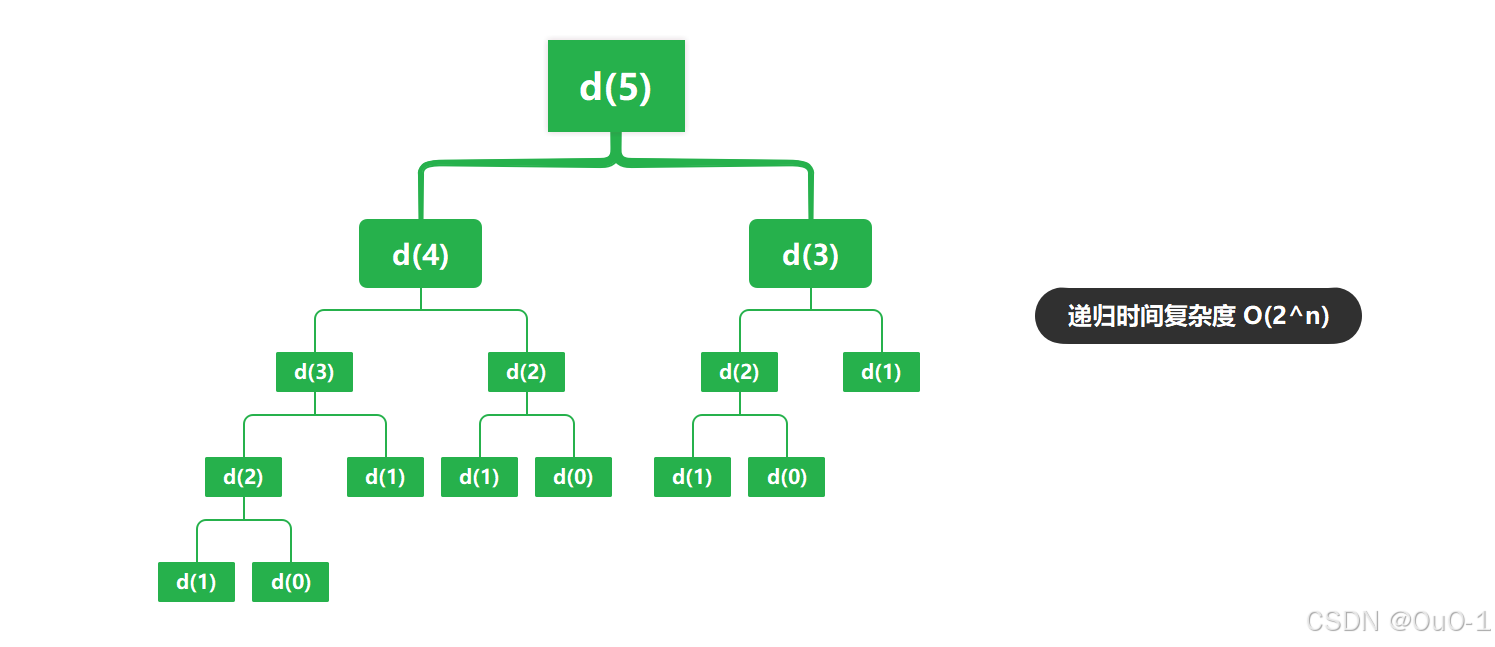
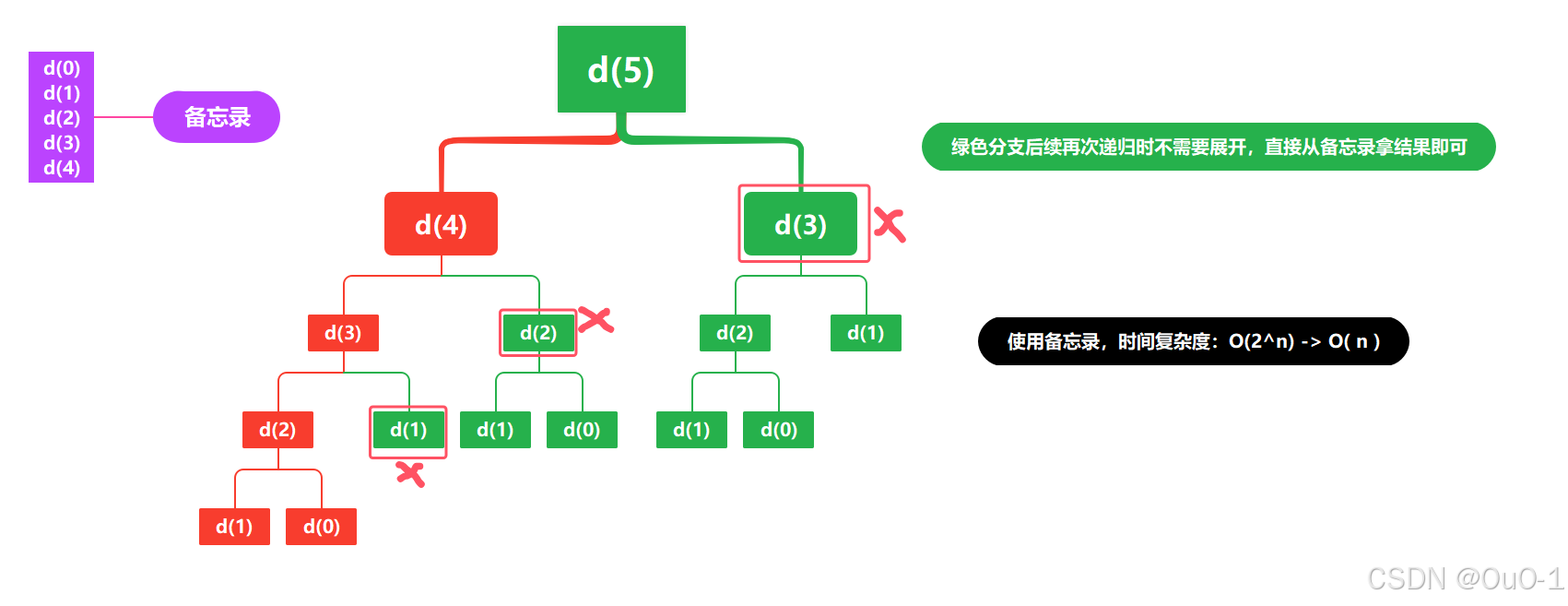
    解法二：记忆化搜索   

当我们在递归的时候，发现递归过程会重复进行完全相同的问题，我们就把这些完全相同的问题存储到额外创建的"备忘录"中，再后续递归出现相同问题，直接从备忘录中拿计算好的结果即可，避免不必要的重复递归； 

所以记忆化搜索，就是一个带备忘录的递归；记忆化搜索，其实也是剪枝的一种方式，在本题使用记忆化搜索，就能把指数级别的时间复杂度降到常数级别；

本题我们存的可变参数和返回值的映射是< index , memory[ index ] >，表示< n , fib (n) >;

    编写代码       

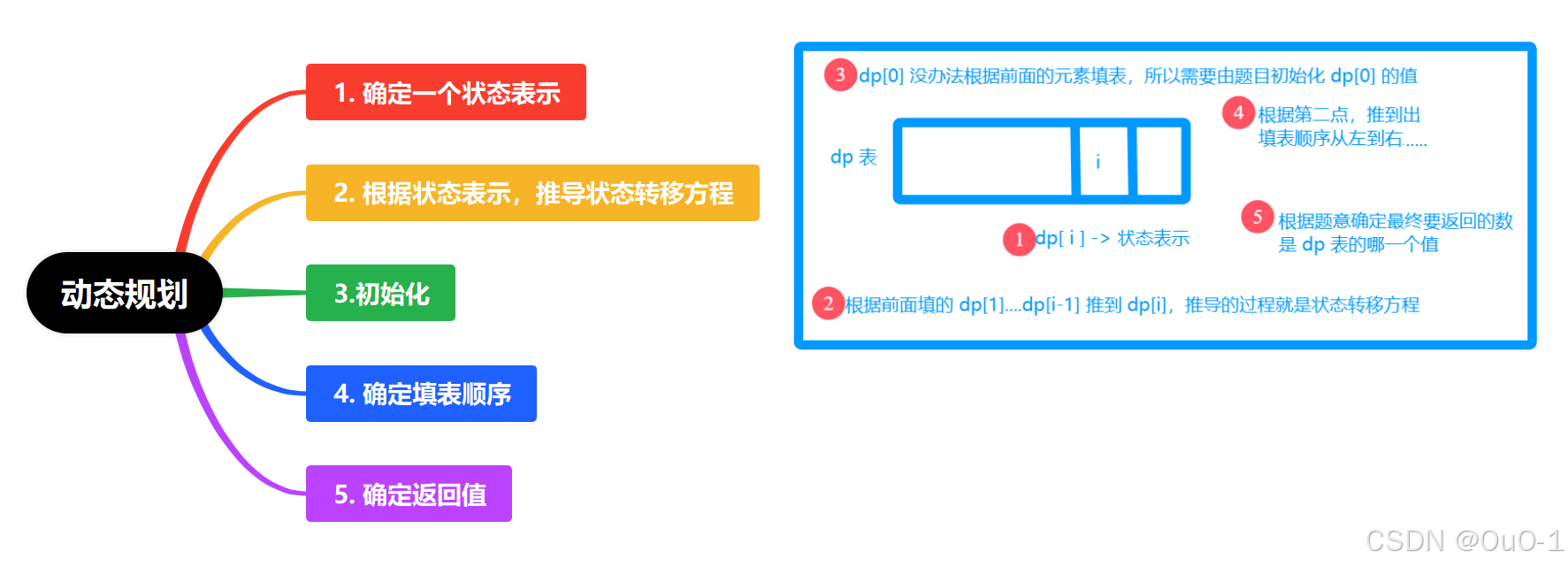
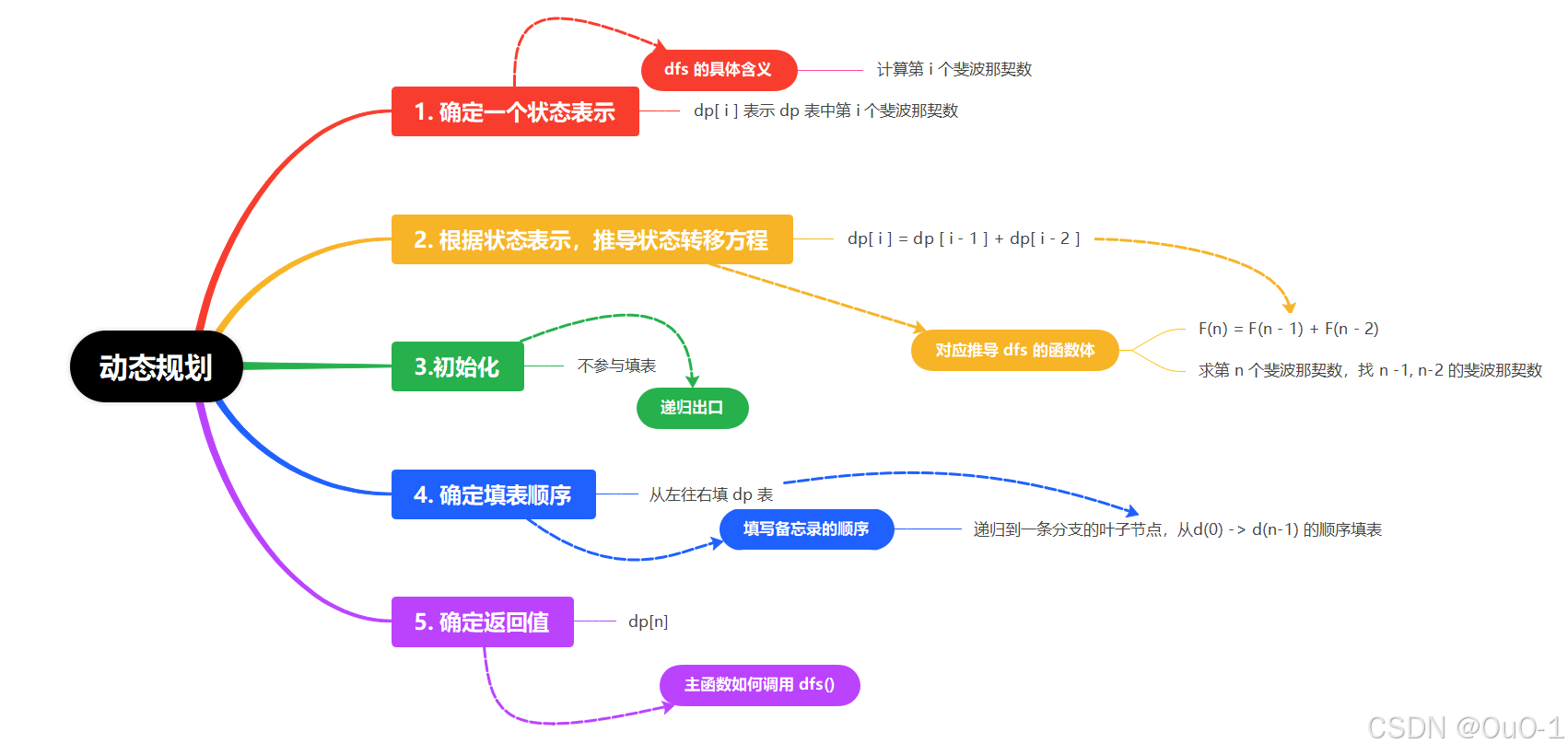
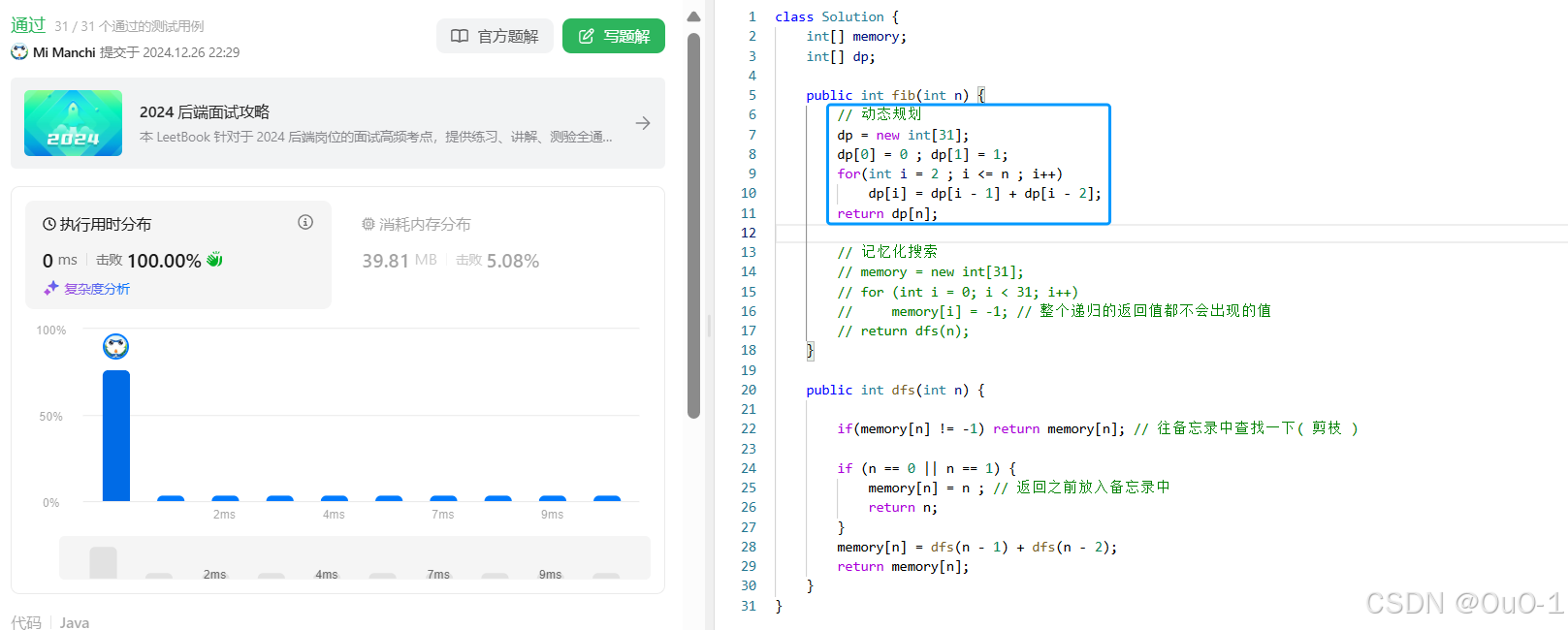
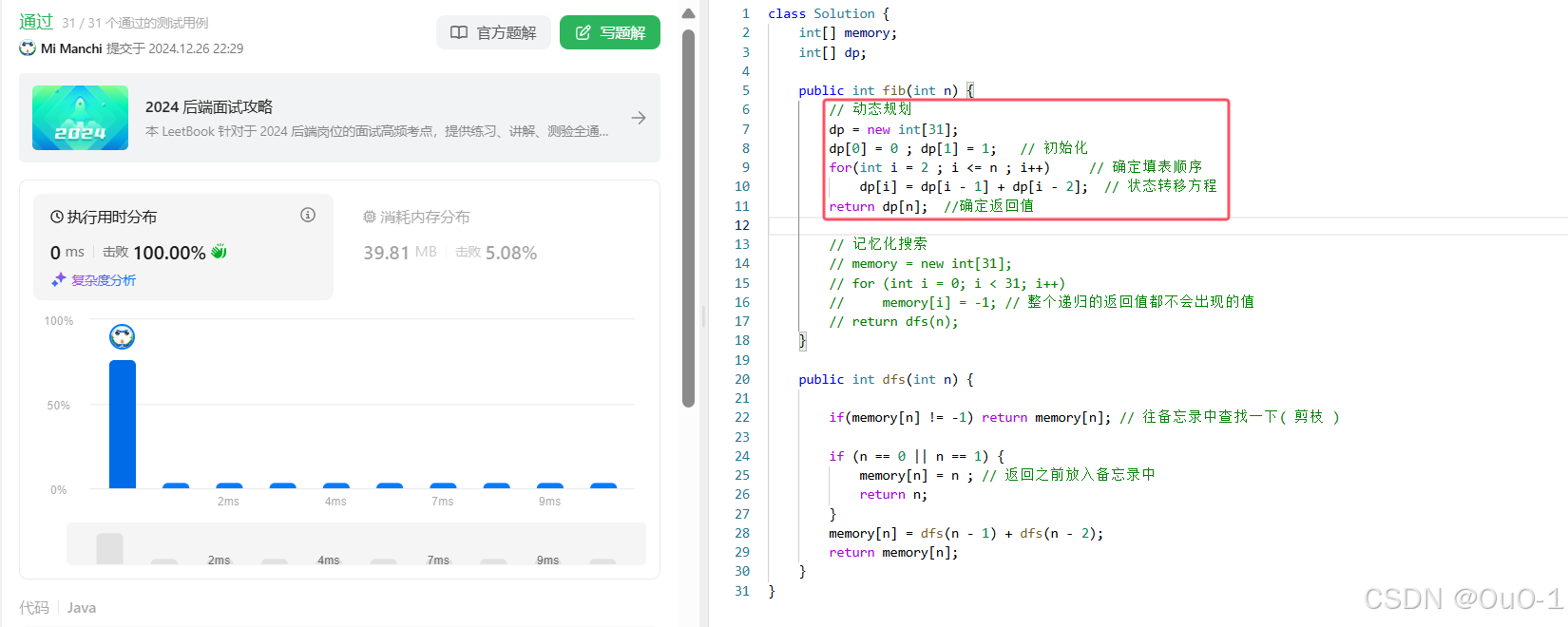
    解法三：动态规划   

动态规划简单介绍

我们可以通过递归，来推出上面动态规划的五步，因为它们是一 一对应的关系 ；

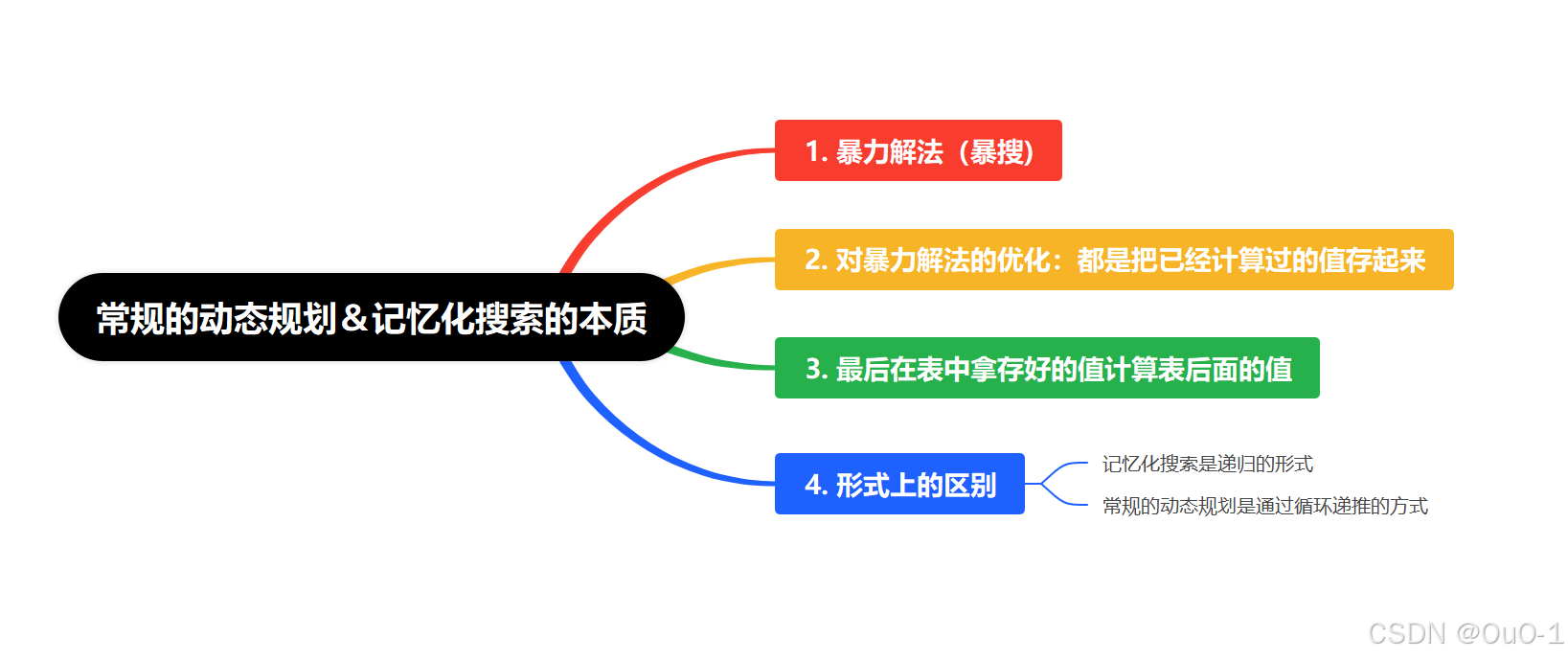
    常规的动态规划＆记忆化搜索的本质     

    编写代码       

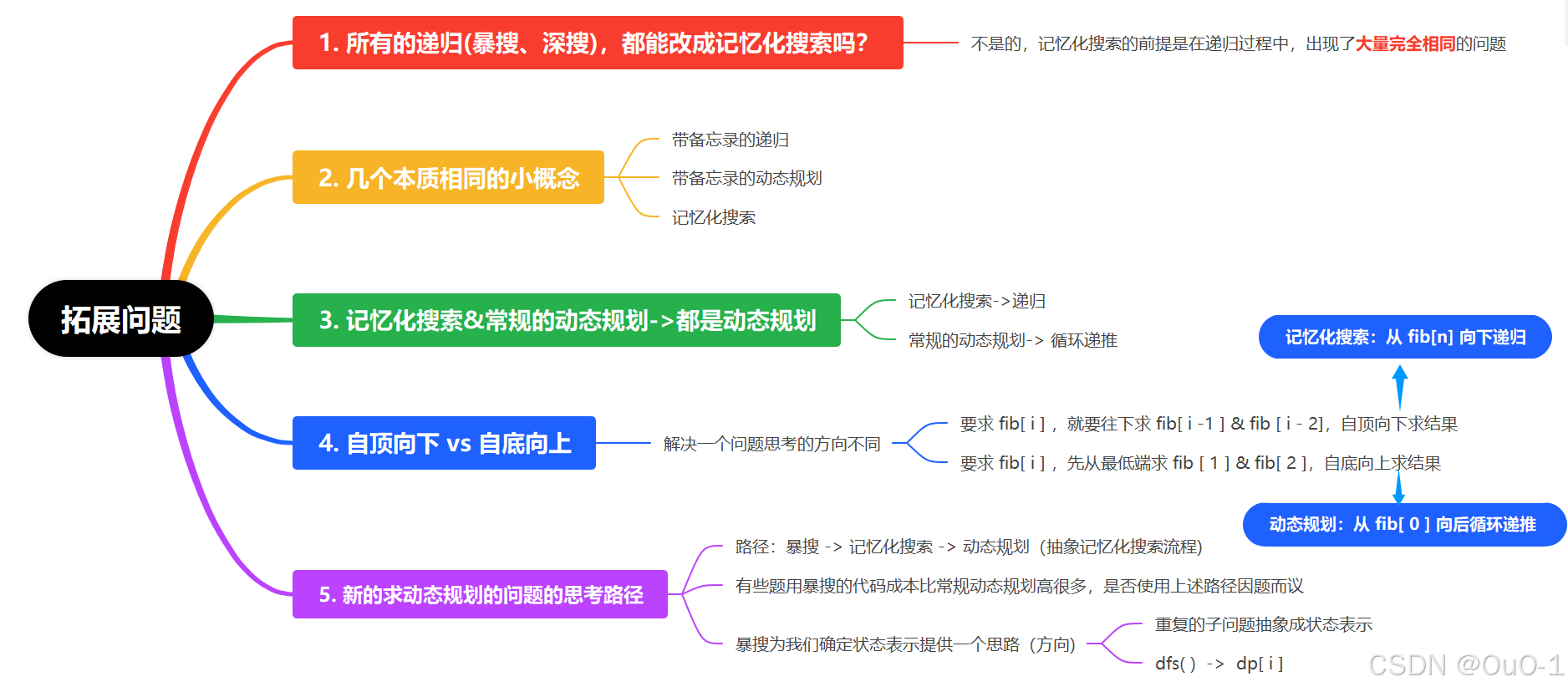
    拓展问题     

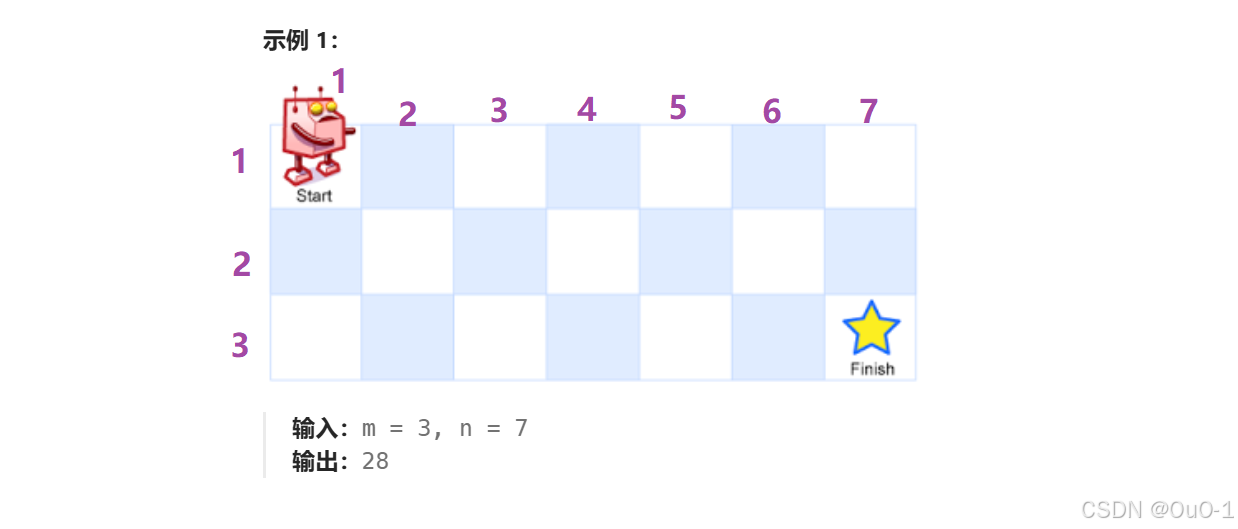
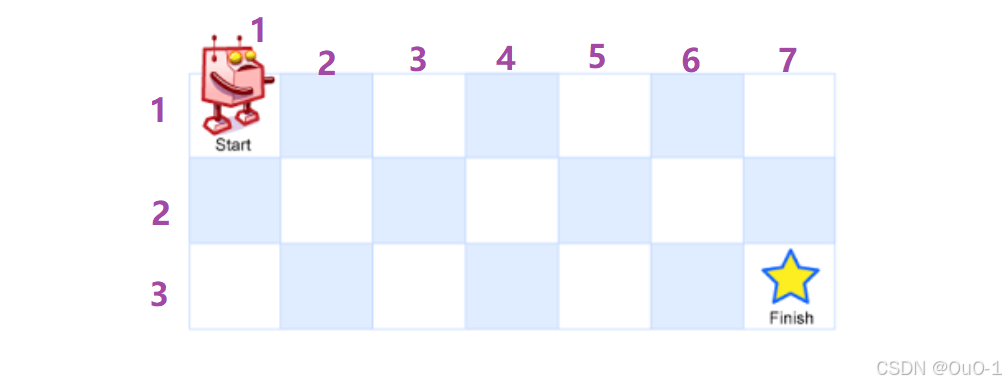
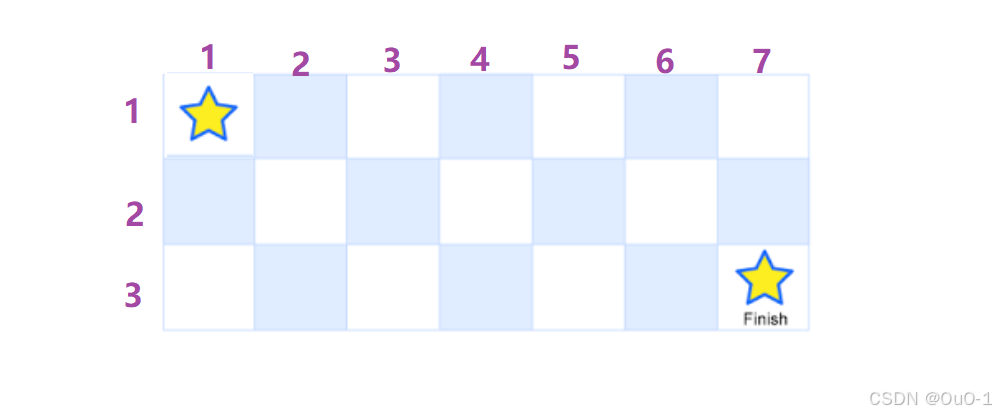
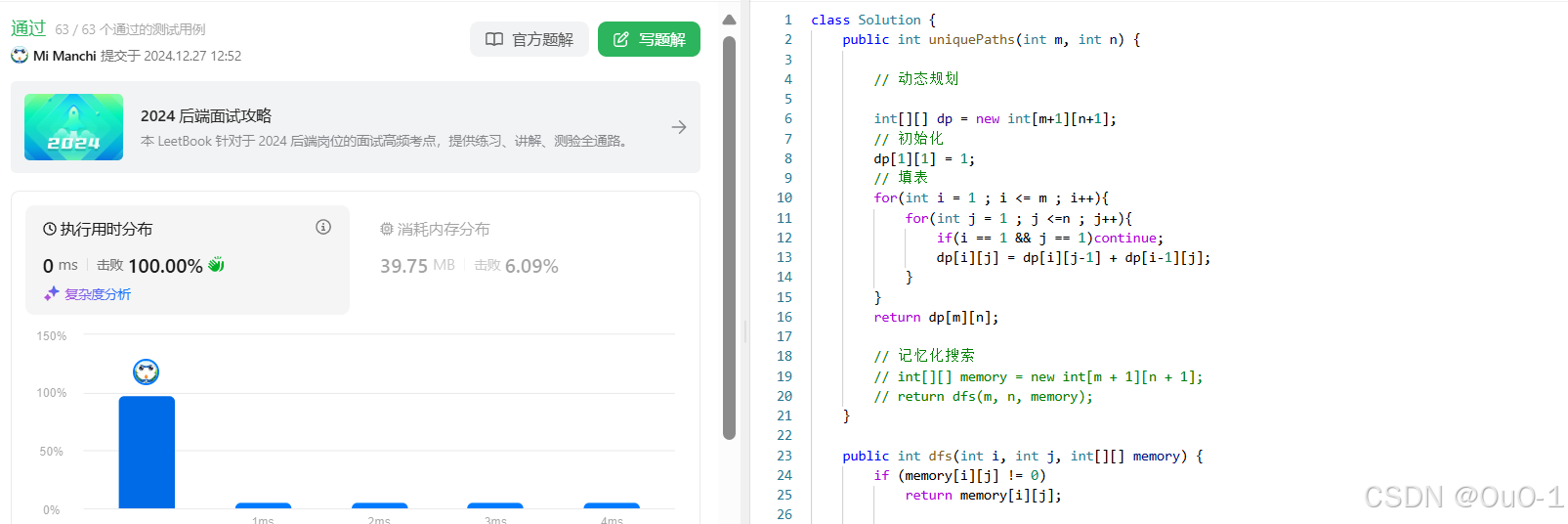
不同路径

    题目解析    

为了避免处理过多边界情况，我们从下标1开始计数： 

    算法原理    

    解法：记忆化搜索    

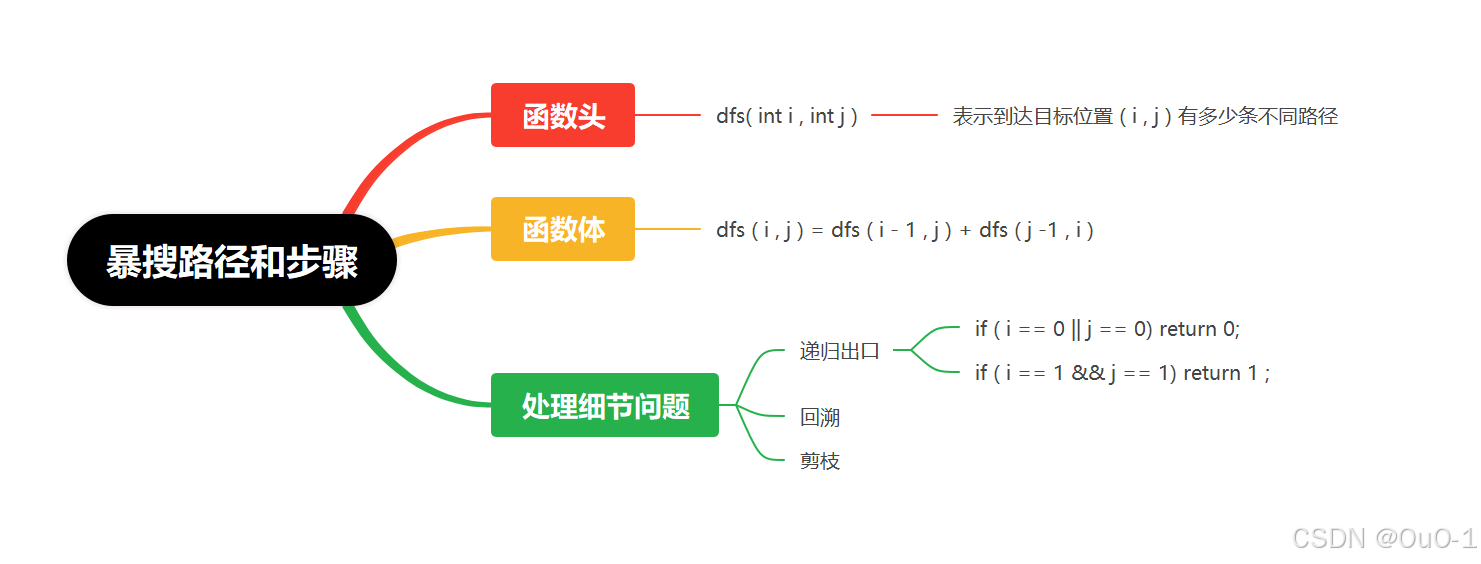
    1. 写出暴搜代码    

    函数头   

我们直接定义 dfs(int i , int j)，给 dfs() 的任务：表示给一个坐标，通过递归求出，到达( i , j ) 坐标一共有多少种方法；

    函数体     

如果机器人想要到达一个位置，我们只需要关心到达这个目标位置的前一个位置即可，而前一个位置有两种情况：

如果我们知道：到达上面的圆圈有多少种方式，那么我们直接走到目标位置即可；

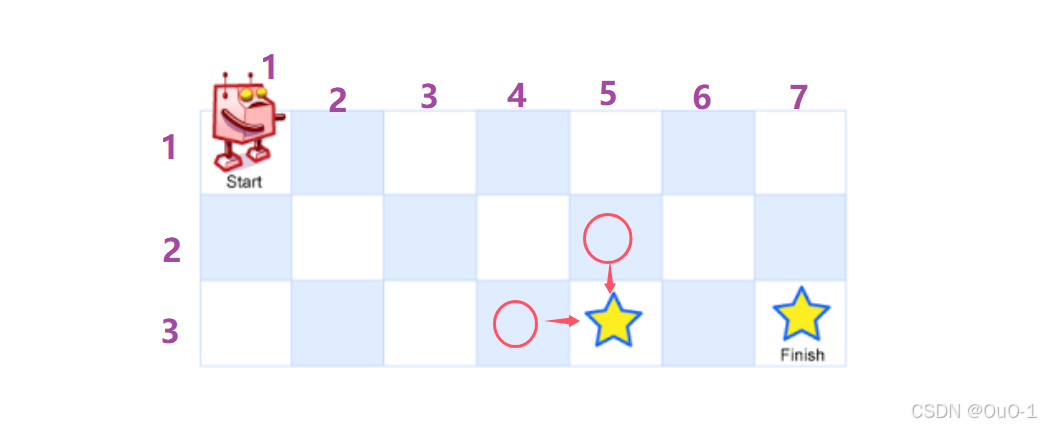
到达目标位置的路径数 = 目标位置的前一个位置的所有情况对应路径数之和；

dfs( i , j ) = dfs ( i - 1 , j ) + dfs ( i , j - 1 ) ( i > 0 && j > 0)

    递归出口    

目标位置是 ( 1 , 1 )，dfs( 1 , 1 ) = dfs ( 0 , 1 ) + dfs ( 1 , 0 ) ，此时就会出现越界情况；

所以递归出口 if ( i == 0 || j == 0 ) return 0 ，表示能到达 ( 0 , j ) 或者 ( i , 0 ) 的路径数之和为0； 

还有一个递归出口，if ( i ==1 && j == 1 ) return 1，表示位于起点，路径数之和为 1

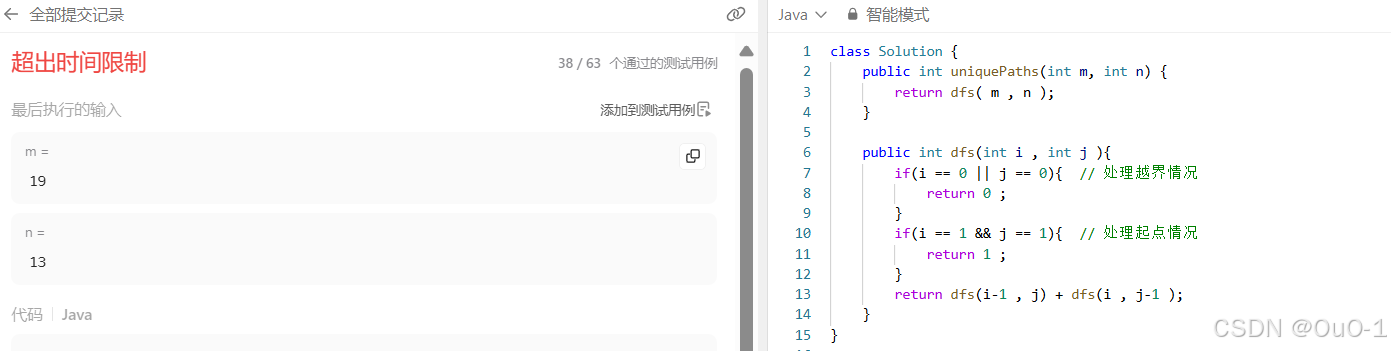
    编写代码     

    暴搜转换成记忆化搜索      

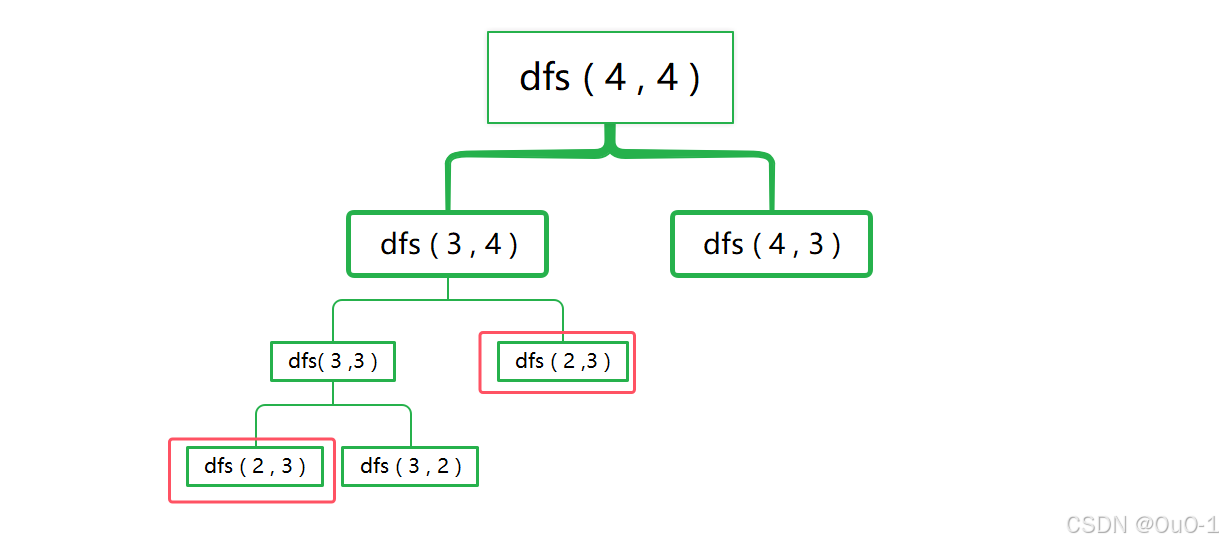
    发现重复问题     

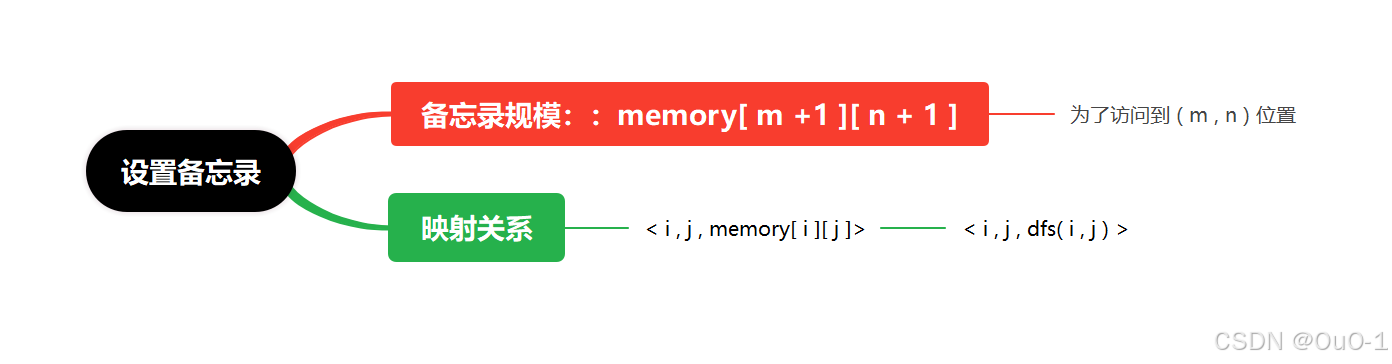
    添加备忘录    

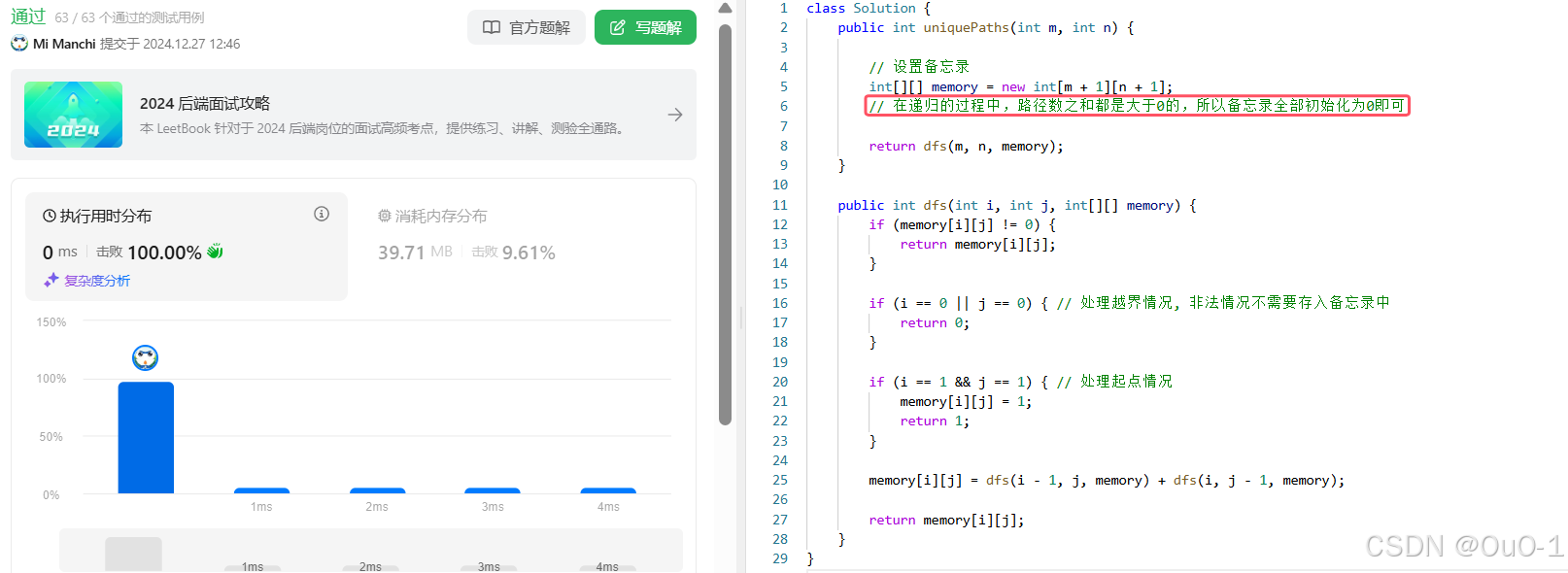
    编写代码       

    处理细节问题    

     修改成动态规划代码    

最长递增子序列

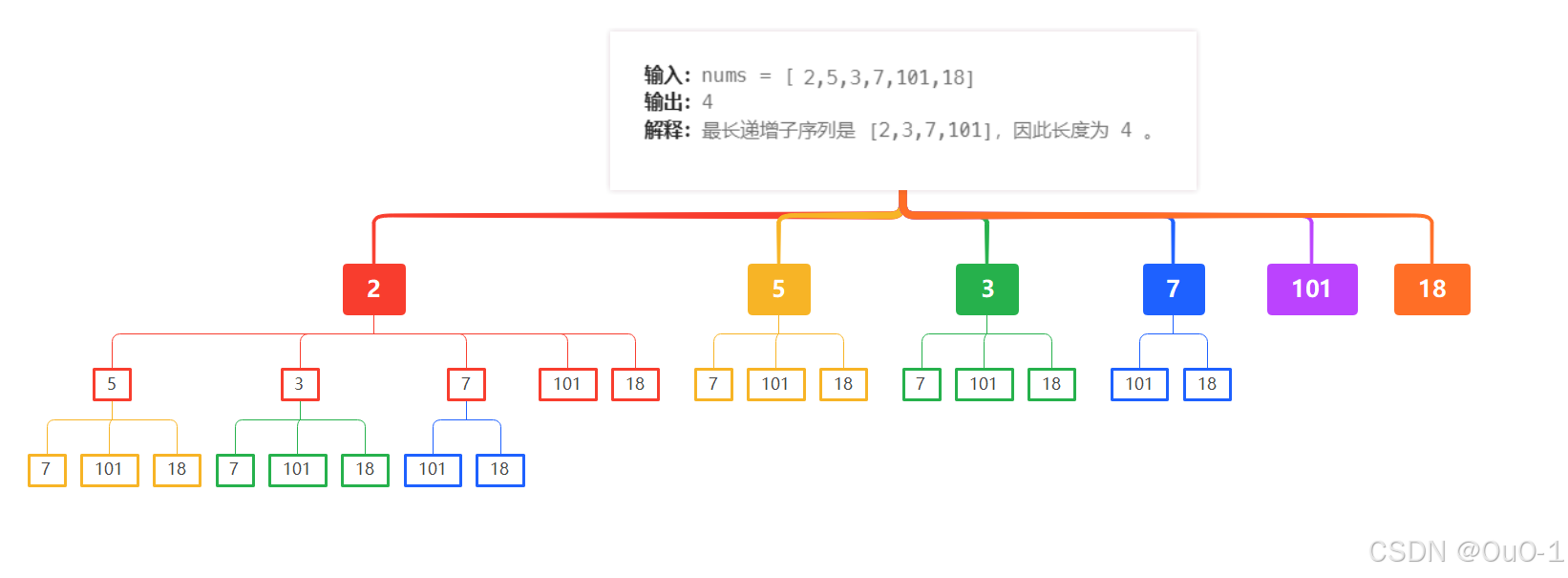
    题目解析    

    算法原理    

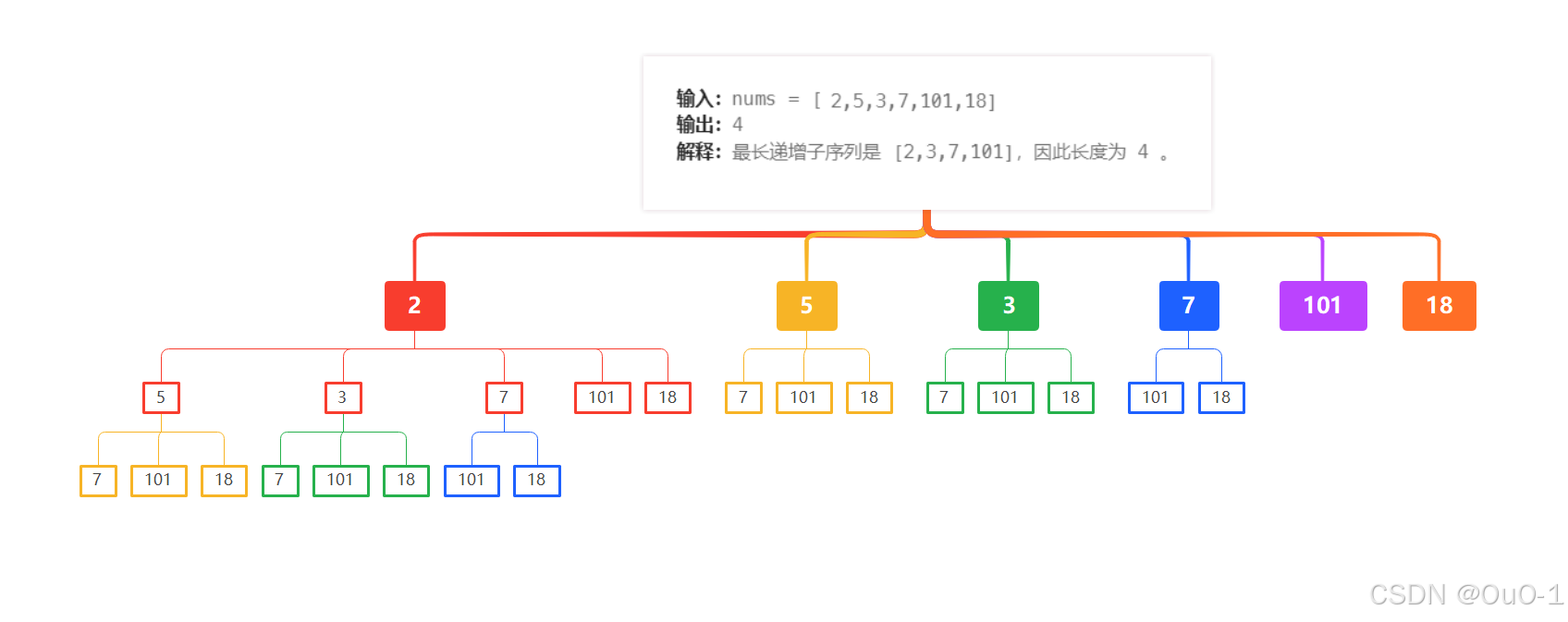
我们以这个例子进行讲解 

     递归     

 对于本题，要找出最长递增子序列，我们就可以先暴力查找所有递增子序列，在这些递增的子序列中，找到长度最长的子序列即可；

    函数头   

我们要找的是最长递增子序列的长度，所以 dfs 的任务：给一个起点，后续找出以这个起点的最长递增子序列长度；int dfs( int pos ) ，返回以 pos 为起点的最长递增子序列长度；

    函数体    

函数体会找以 pos 为起点之后的递增子序列的最大值 ，最大值+1 就是最终的返回值；

    递归出口     

本题不需要递归出口，因为我们使用的循环不会越界； 

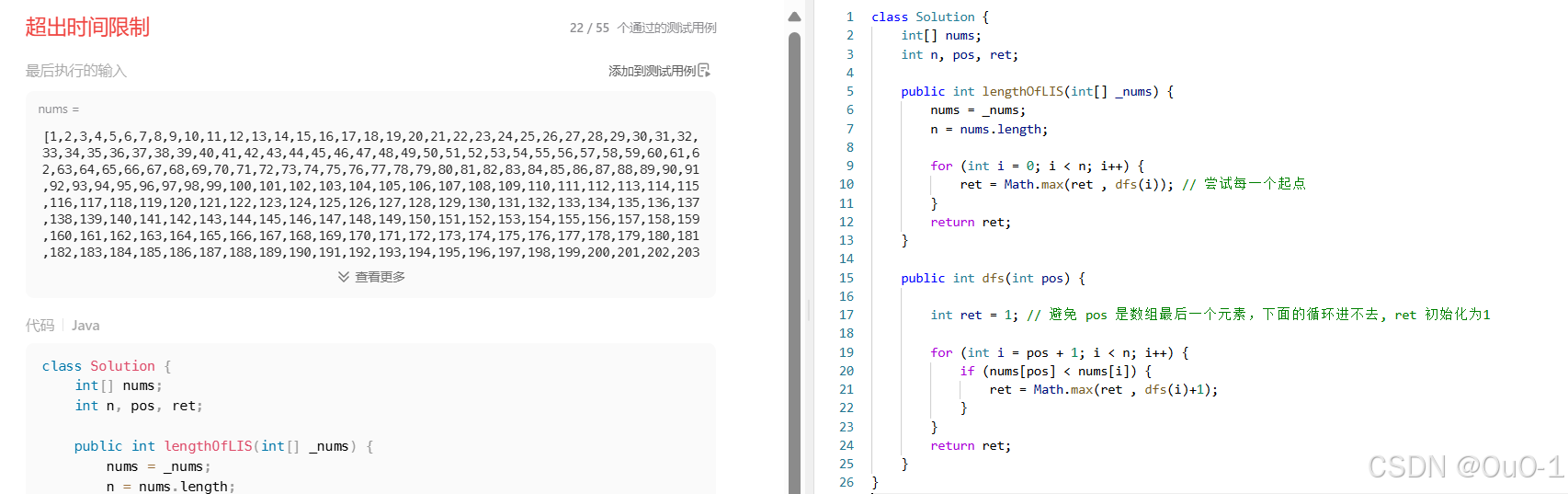
    编写代码        

这个 dfs 其实写出来要考虑很多东西，所以暴搜 -> 记忆化搜索 -> 动态规划这条思考路径也没有那么好用；

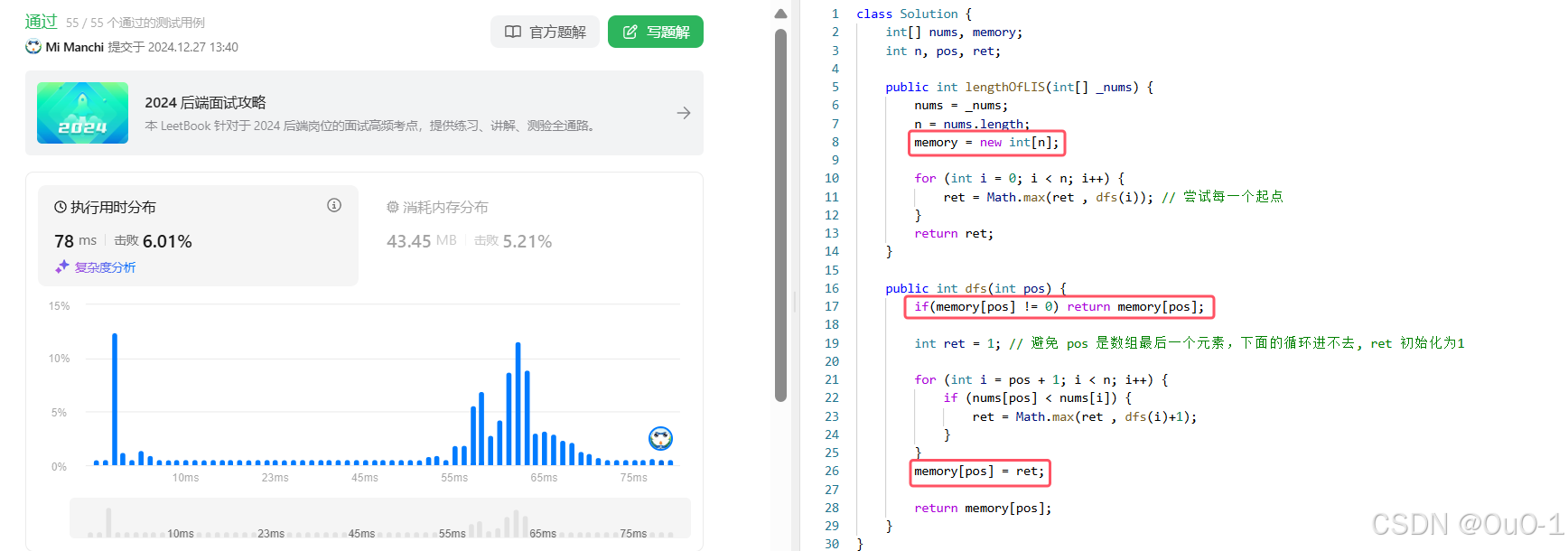
     暴搜修改为记忆化搜索    

    重复子问题    

    编写代码       

这道题使用记忆化搜索的时间复杂度高，是因为这道题的最优解是贪心算法； 

    细节问题    

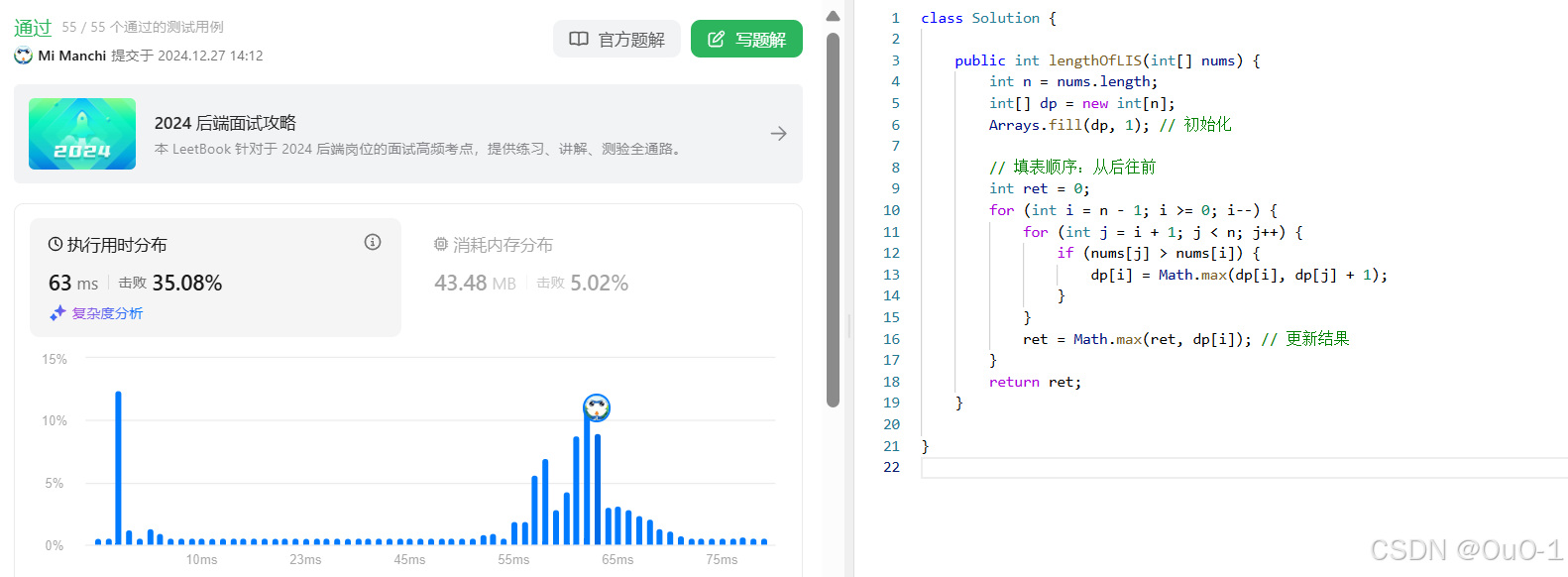
    动态规划    

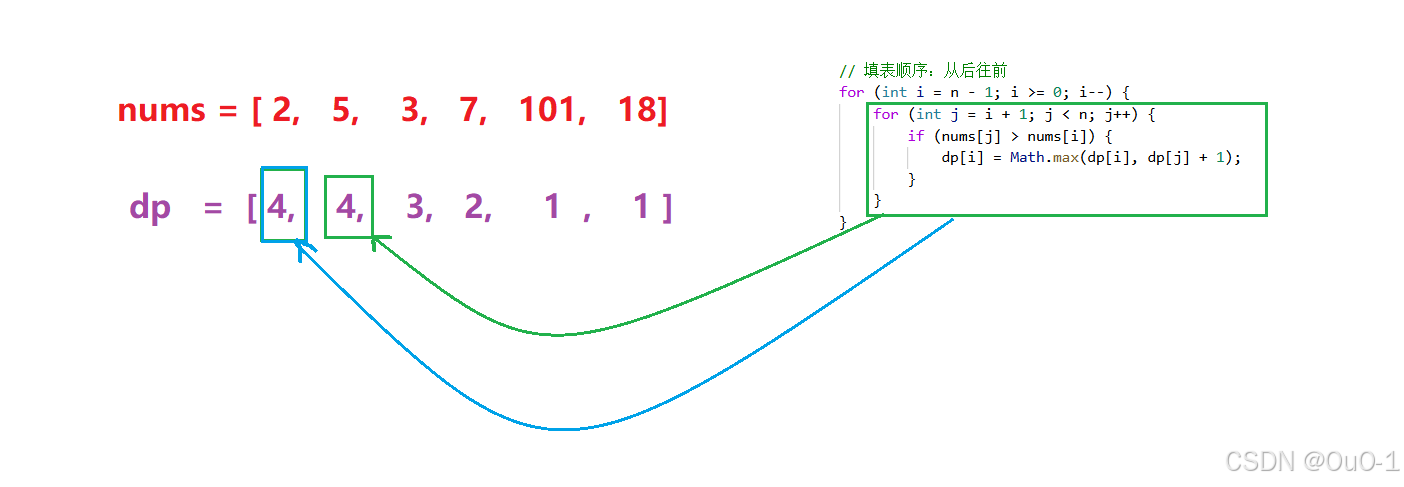
    注意填表顺序    

我们这里解释一下填表顺序为什么是从后往前，我们先来看记忆化搜索的 dfs 函数体：

求 dfs( pos ) 时，是依赖 dfs( pos+1 ) 以及往后位置的值，因此我们在填 dp 表的 dp[ pos ]，也需要依赖 dp[ pos+1 ] 以及 pos +1 后面的值，所以后面的值要先算出来；

    解释状态表示 dp[ i ]     

第二层循环用于遍历以 i+1 为起点后面的所有序列元素， 并且把最长递增子序列长度填入对应 dp 表中：

 此时 dp[ i ] 存的是以 i 为起点的最长递增子序列的长度;

所以如果 nums[ i ] 是最大的元素，那么dp[ i ] =1；

    注意返回值     

我们填表的时候， dp[ i ] 记录的是以 i 这个位置的最长递增子序列的值和 i + 1 位置最长递增子序列的最大值； 

但是返回值不是 dp 表某一个元素，而是 dp 表中所有元素的最大值；

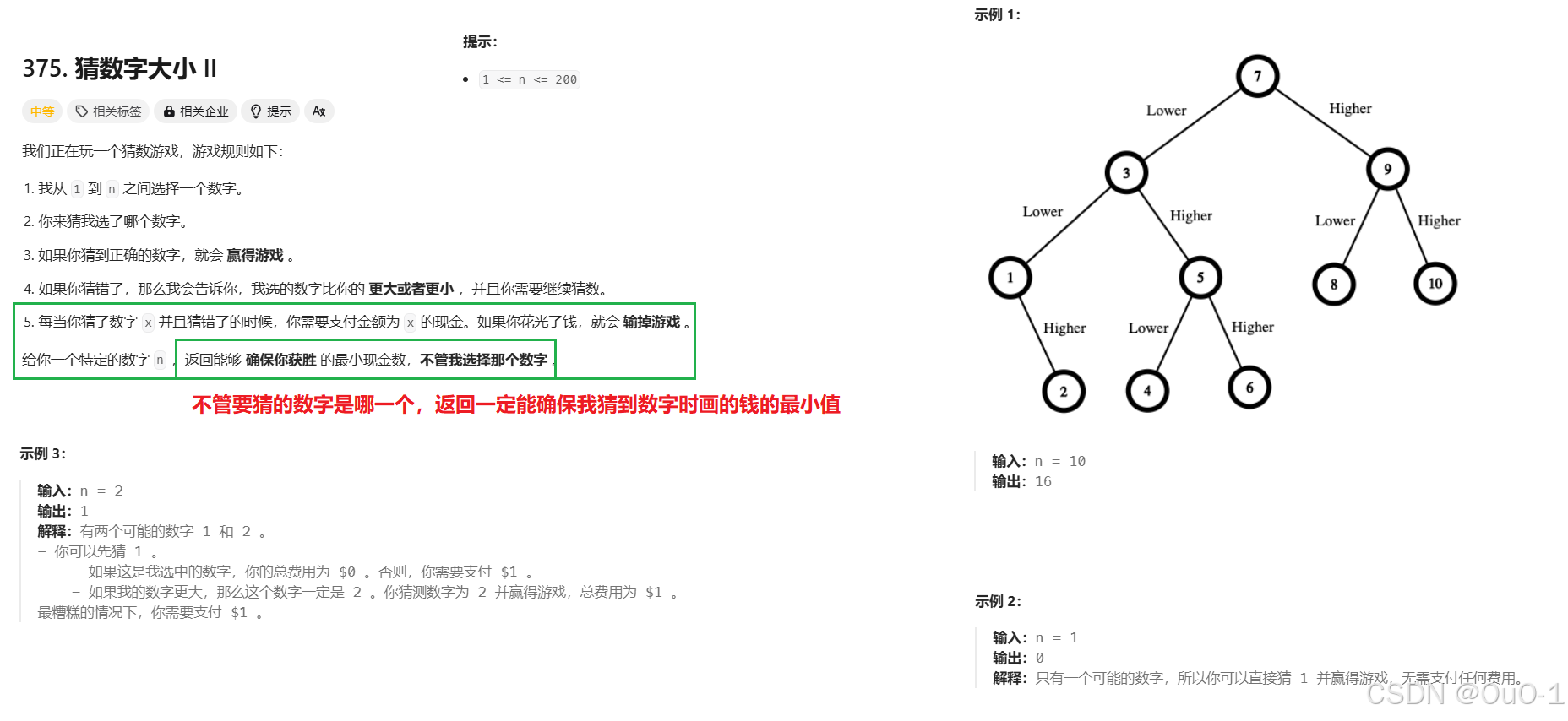
猜数字大小Ⅱ

    题目解析    

    算法原理    

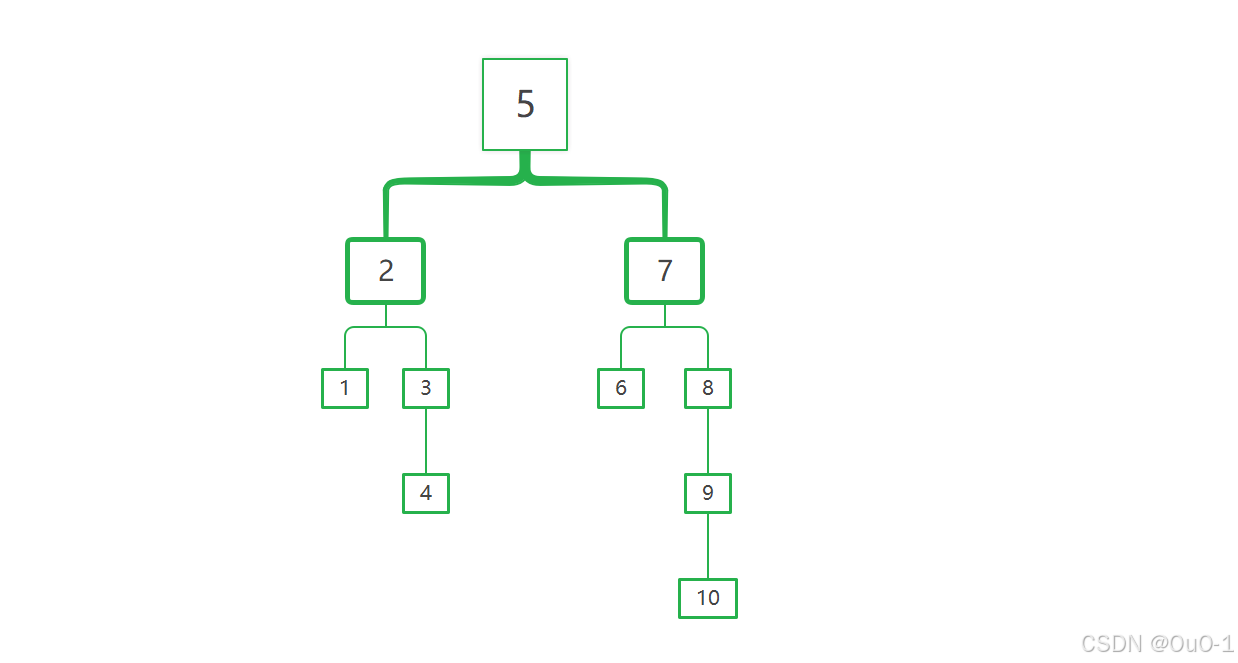
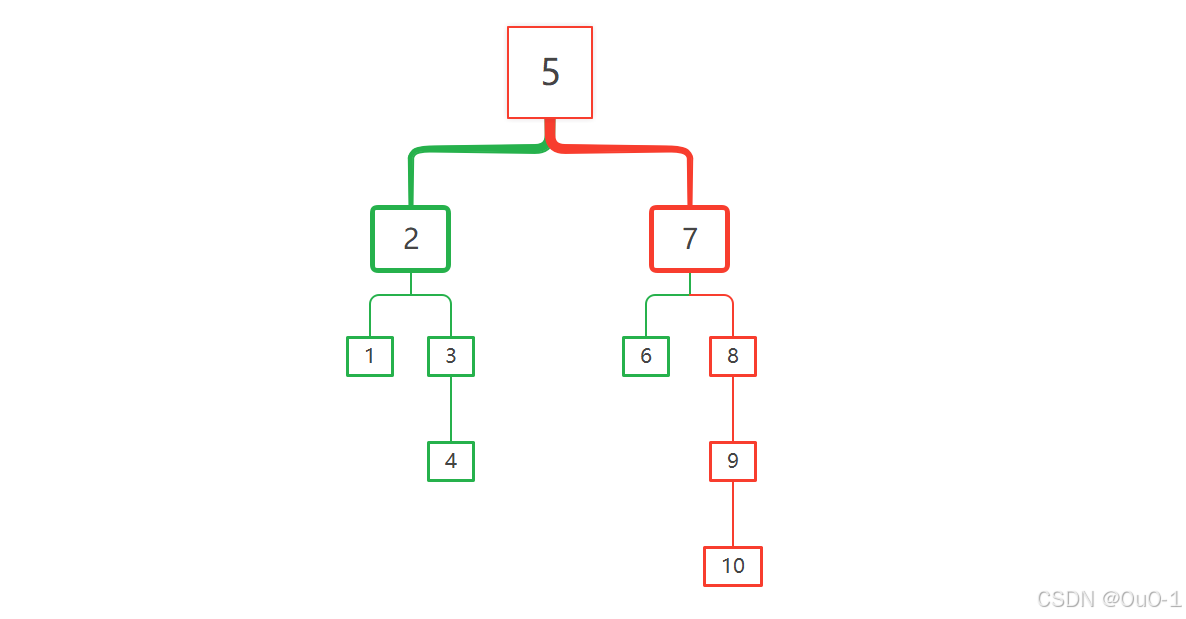
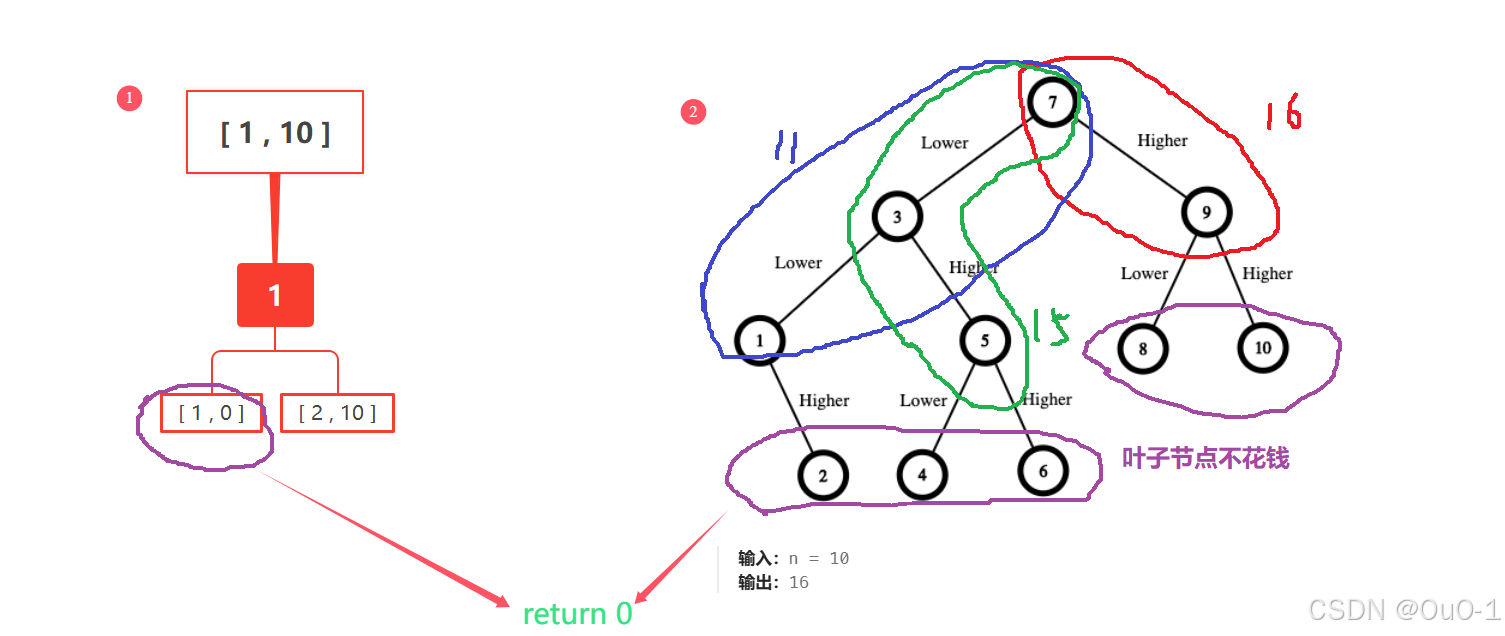
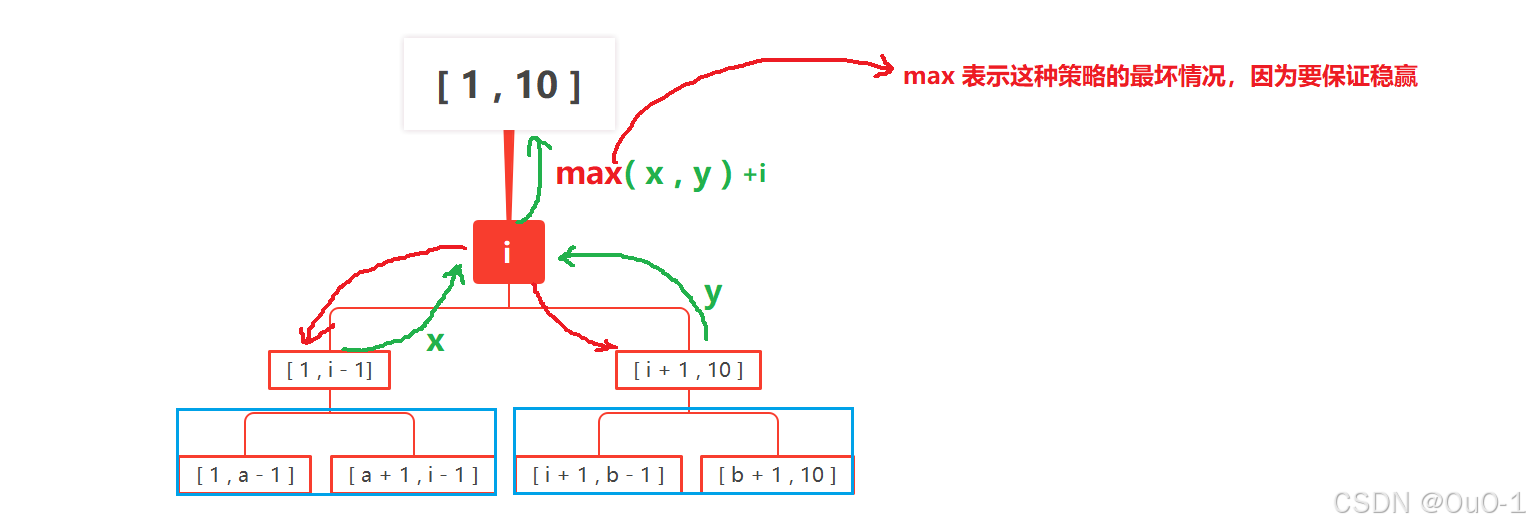
假设给的 n = 10，那么如果我们采用二分查找策略：

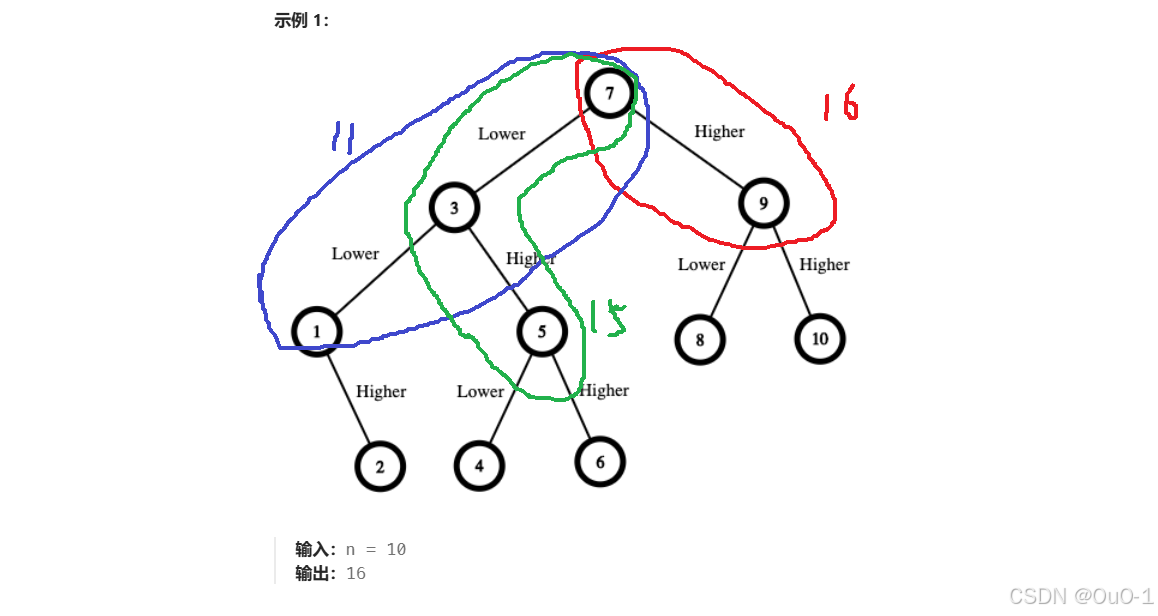
虽然能在一般情况下最快速地找到要猜到的数，但是我们保证赢的情况下（采取的决策面临的最坏情况)，至少需要花的钱为决策树最长分支各个节点的总和：

所以对于这题，二分查找策略并不是最优解，最优解：

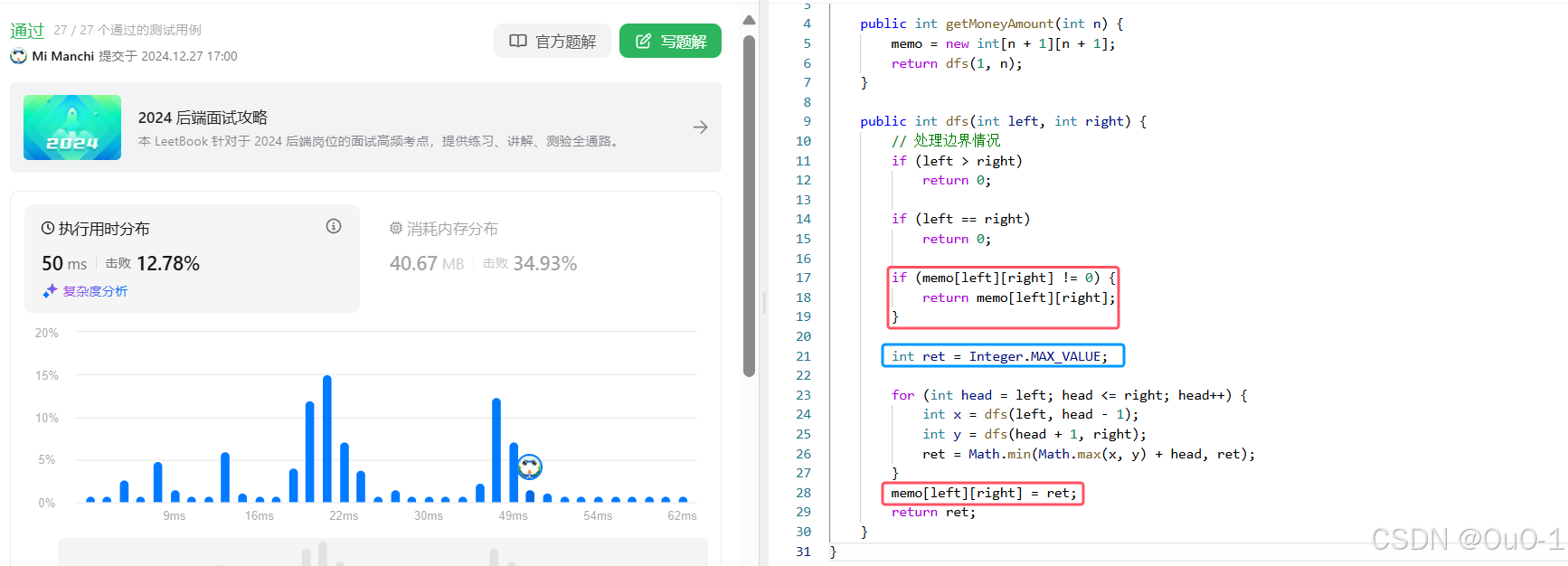
    暴搜    

 我们要的是所有情况下的 i 拿到的所有最大值分支中，最小的那条分支( 合照最后一排最矮的人)；

    处理细节问题    

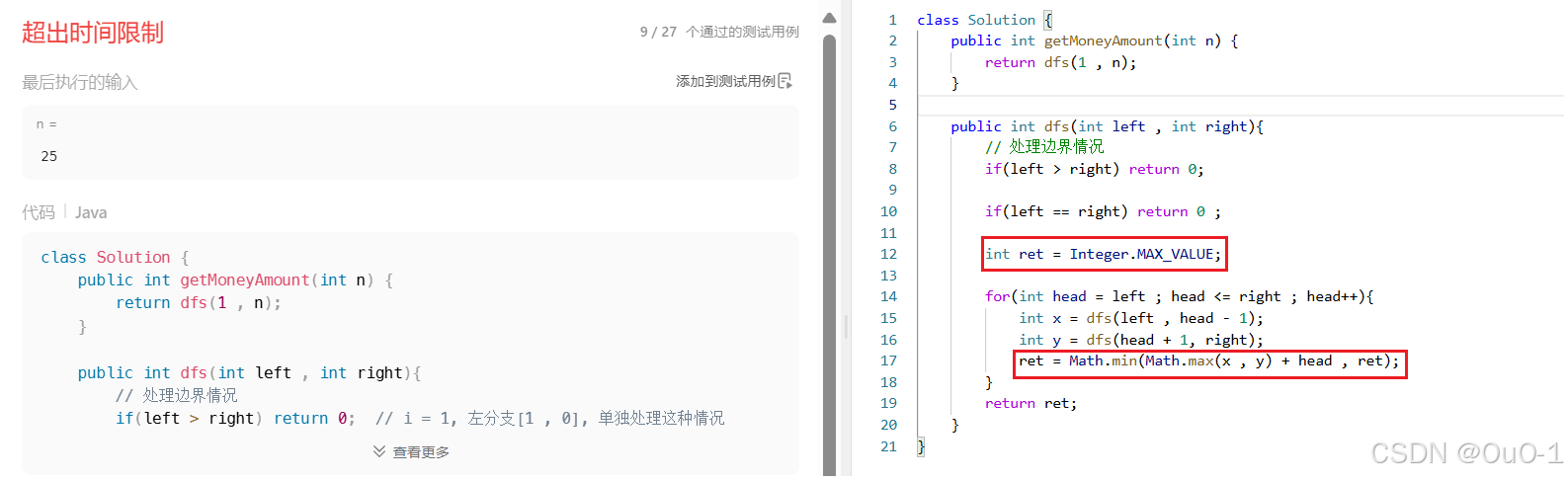
    编写代码        

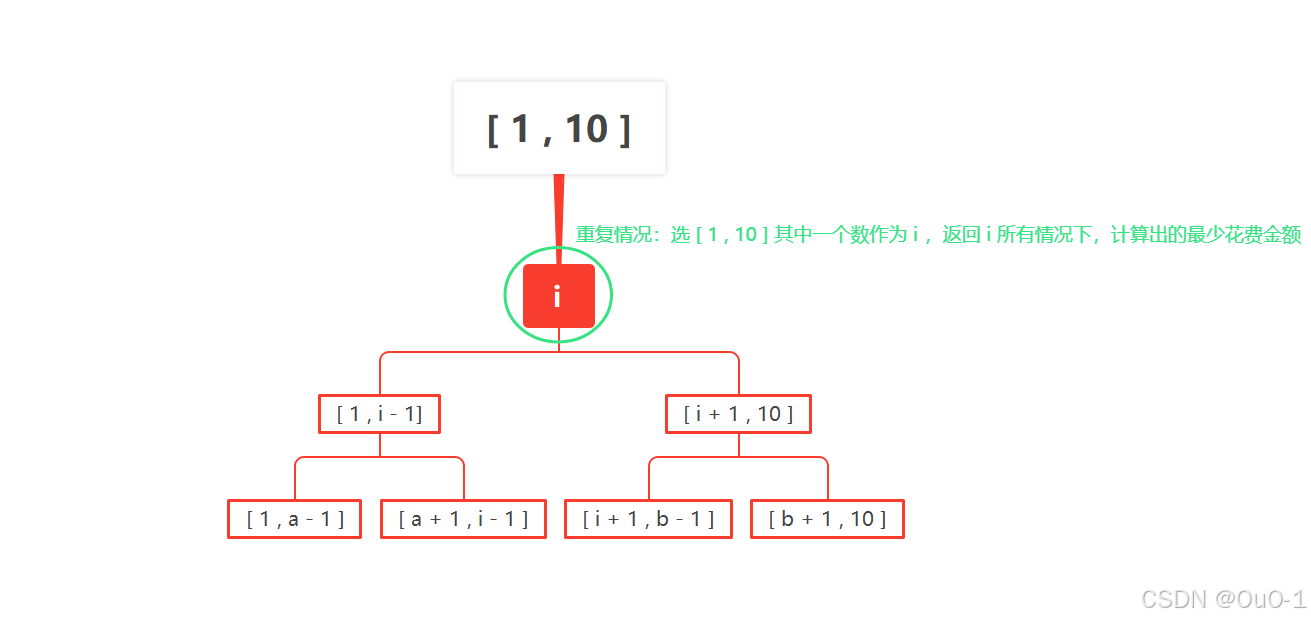
     暴搜修改为记忆化搜索    

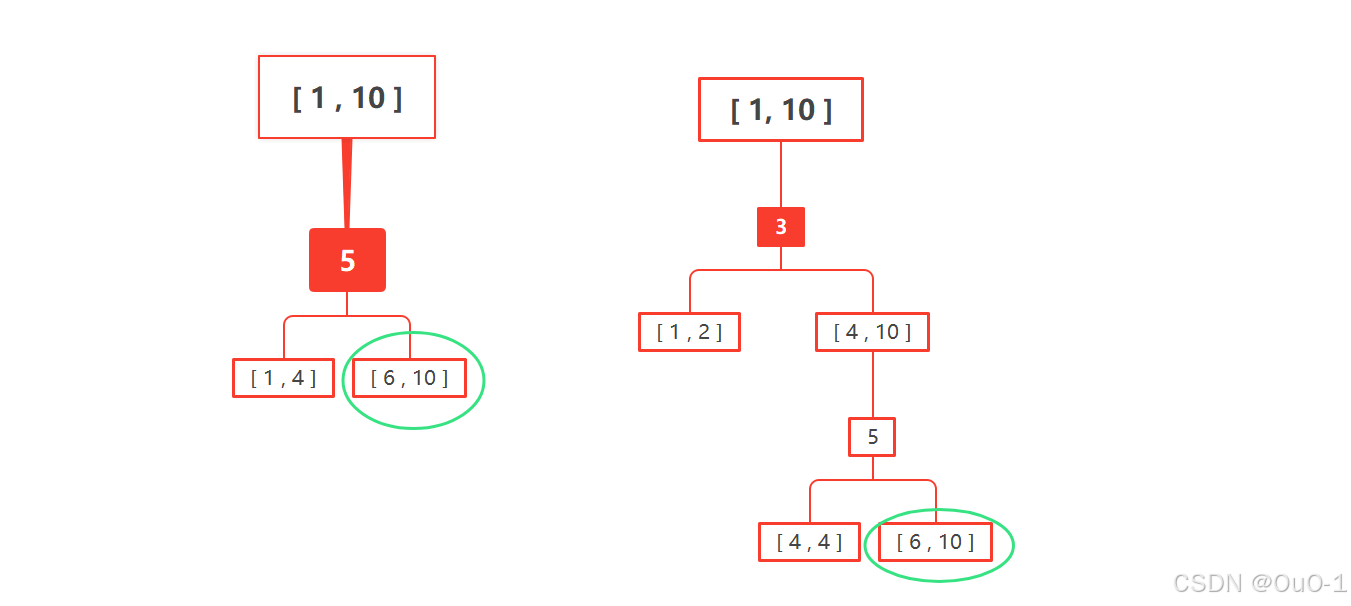
    重复子问题    

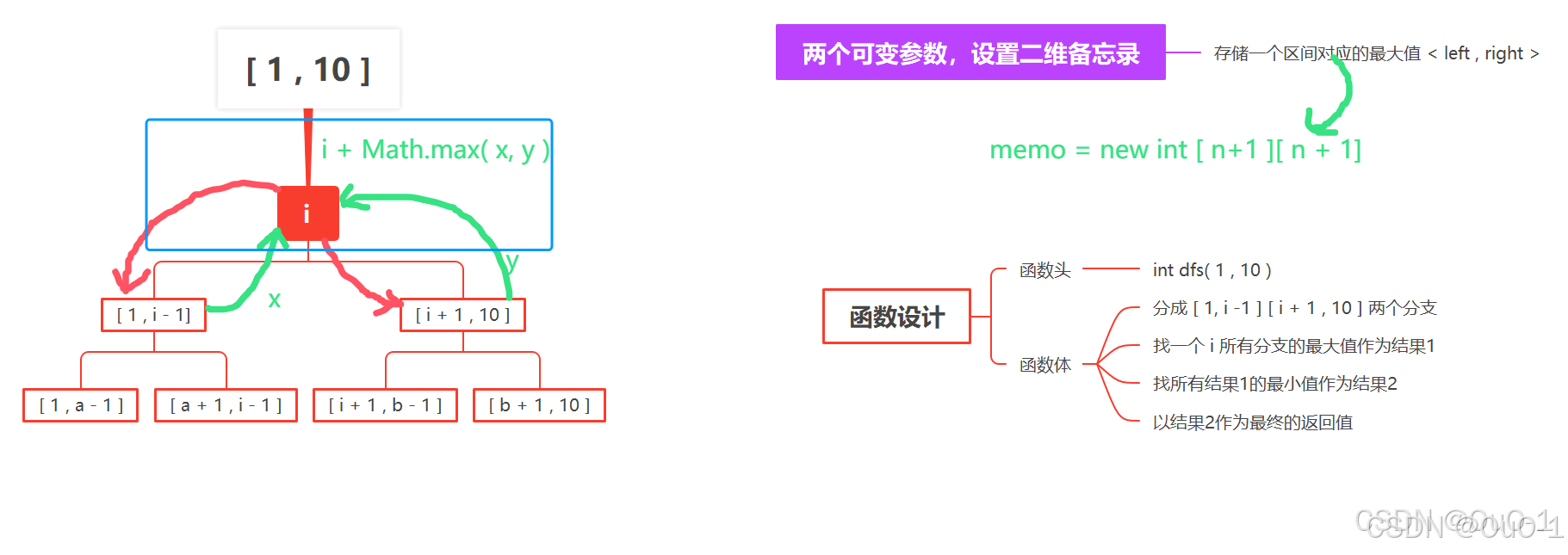
    添加备忘录     

    编写代码       

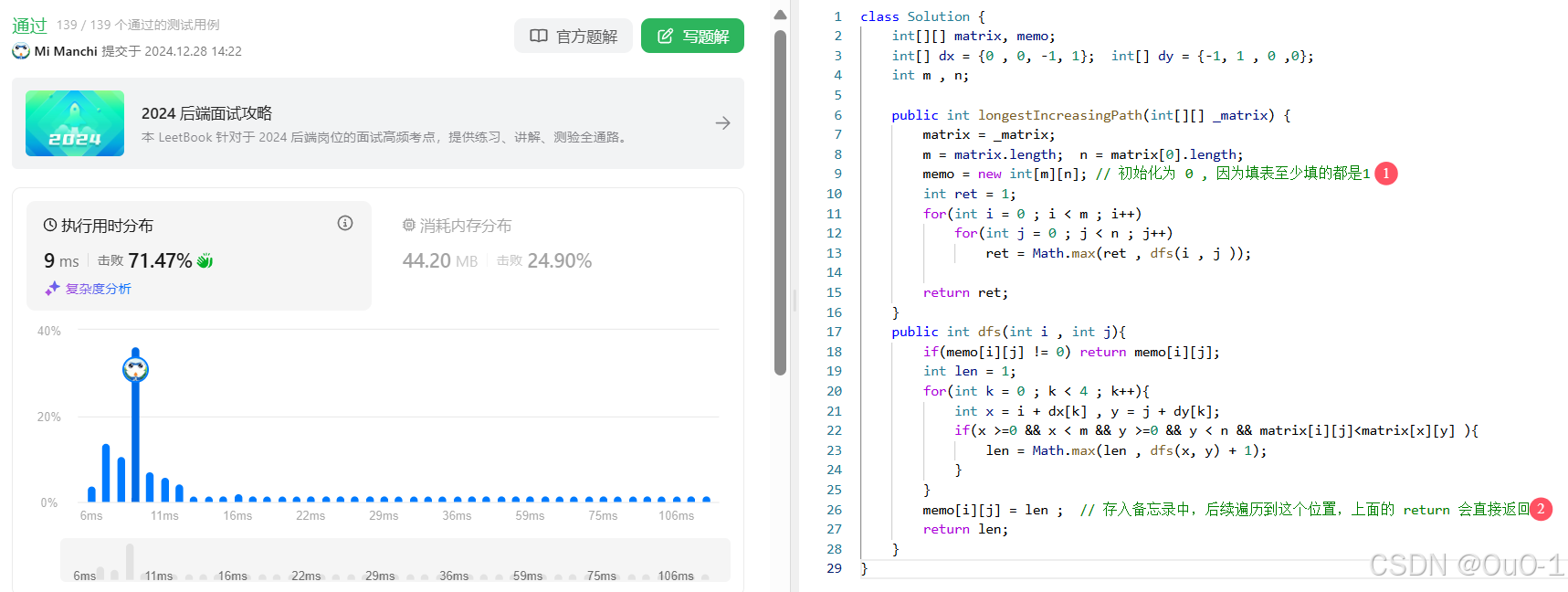
矩阵中的最长递增路径

    题目解析    

    算法原理    

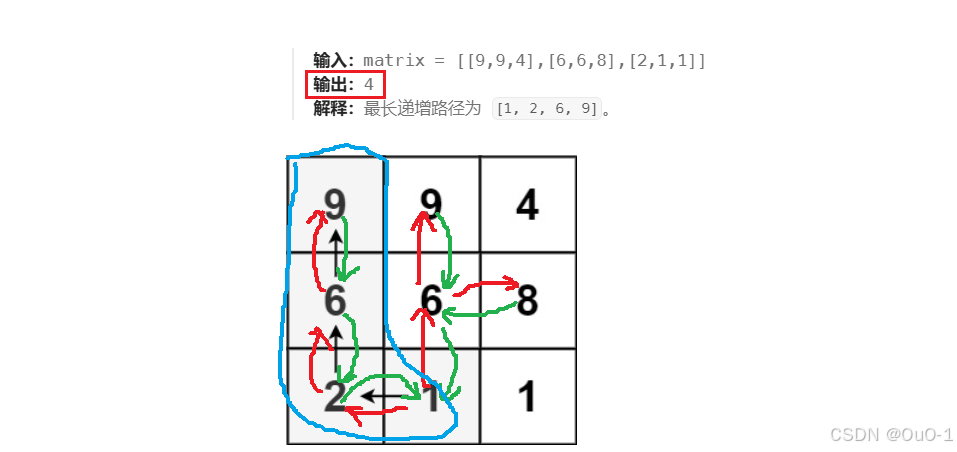
以矩阵的每一个位置为起点进行暴搜，找出每个起点所有的递增路径，返回递增路径的最大值； 

然后最终返回所有起点最长递增路径的最大值即可；

    解法：记忆化搜索   

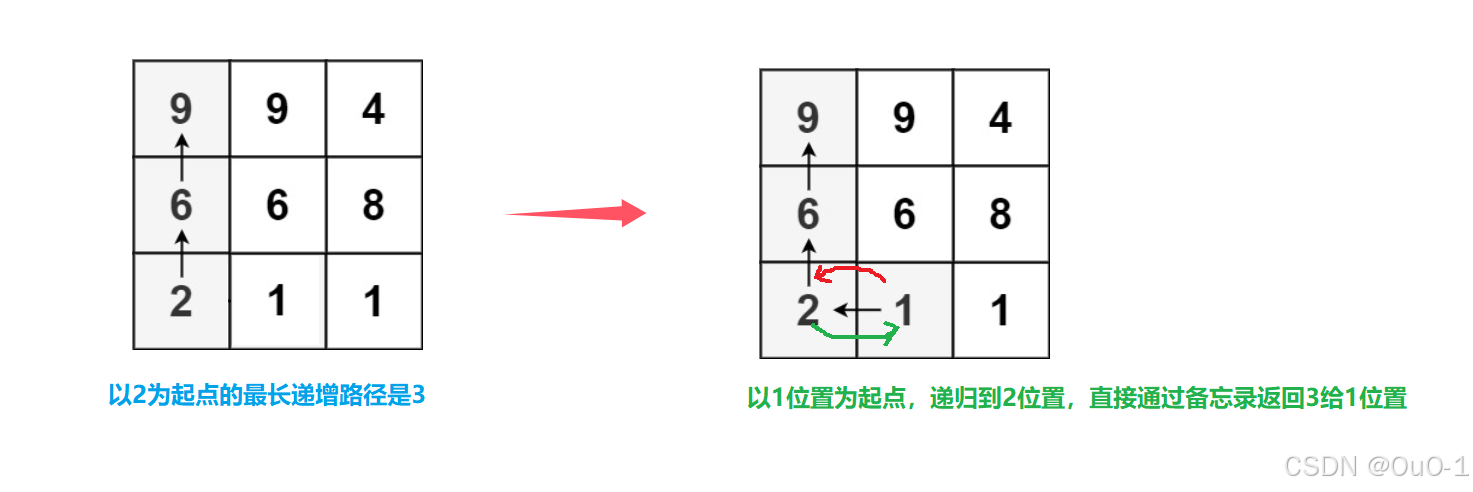
这里可以使用记忆化搜索，是因为当我们以某一个位置为起点时，这个位置的最长递增路径是固定的，我们把这个位置的最长递增路径存在备忘录中；

后续以别的位置为起点，递归到这个位置时，直接向上返回这个位置对应备忘录的元素即可；

    处理细节问题    

    找递增路径决定了不需要设置标记数组     

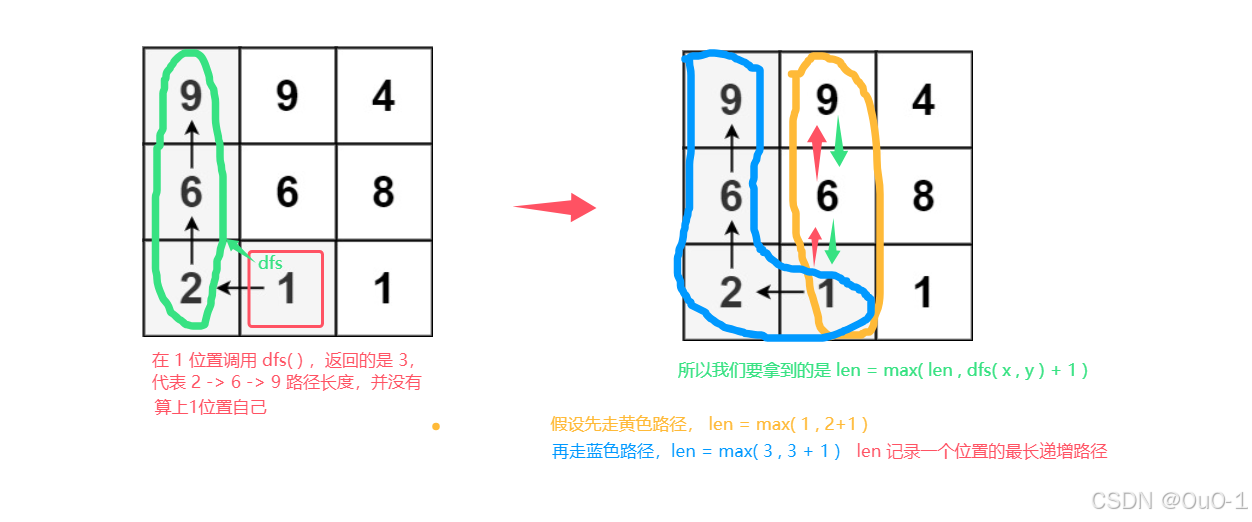
把 len 设置为参数（而不是全局遍历），表示当调用新的 dfs ，把 len 置为1，1 代表已经算上这个位置的方格；

我们每次递归都要找新的 ( x , y ) 的所有递增路径，并且让 len 等于这些路径的最大值；

 我们解释一下为什么要拿 len 和 dfs( x , y ) + 1 进行比较：

    编写代码       

    暴搜    

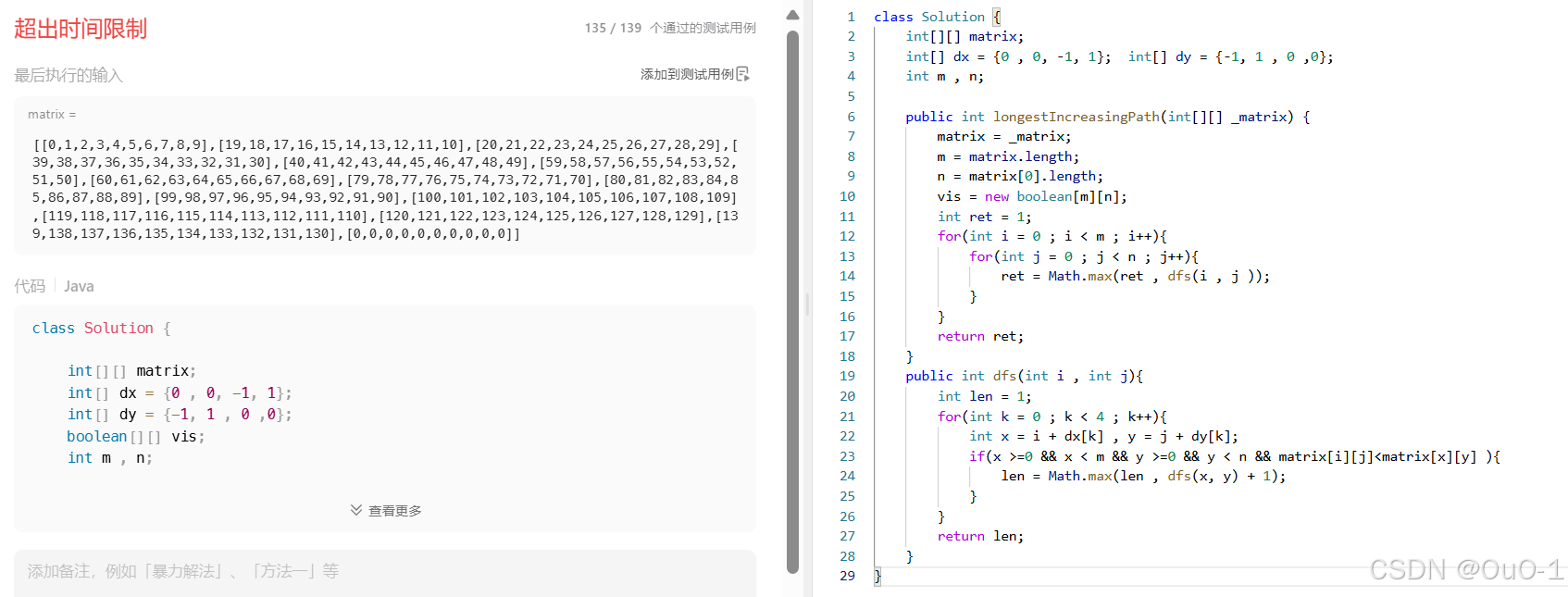
    记忆化搜索    

【递归，搜索与回溯】 专题完结啦！ 撒花 ！😊😊💖💖🎈🎉🎉🎉