#include<stdio.h>
unsigned long long high;
unsigned long long low;
unsigned long long fac(int n,int m){
unsigned long long i,f=1;
if(m!=1){
for(i=n;i>=n-m+1;i--){
f=f*i;
}
return f;}
else if(m==1) {
for(i=n;i>=1;i--){
f=f*i;
}
return f;
}
}
//unsigned long long arrange(int n,int m){
// unsigned long long c;
// c=fac(n,m)/fac(m,1);
// return c;
//}
int main(){
int n,j,t,i,d,x,y,xm,ym;
unsigned long long s1,s2,s,s0;
scanf("%d %d",&x,&y);
scanf("%d %d",&xm,&ym);
s1=fac(xm+ym,xm)/fac(xm,1);
s2=fac(x-xm+y-ym,y-ym)/fac(y-ym,1);
s=s1*s2;
printf("%llu\n",s);
for(i=0;i<xm;i++){
printf("(%d,0)",i);
}
for(j=0;j<=ym;j++){
printf("(%d,%d)",xm,j);
}
for(i=xm+1;i<=x;i++){
printf("(%d,%d)",i,ym);
}
for(j=ym+1;j<=y;j++){
printf("(%d,%d)",x,j);
}
printf("\n");
return 0;} | 成绩 | 10 | 开启时间 | 2024年12月19日 星期四 15:10 |
| 折扣 | 0.8 | 折扣时间 | 2024年12月22日 星期日 23:59 |
| 允许迟交 | 否 | 关闭时间 | 2024年12月29日 星期日 23:59 |
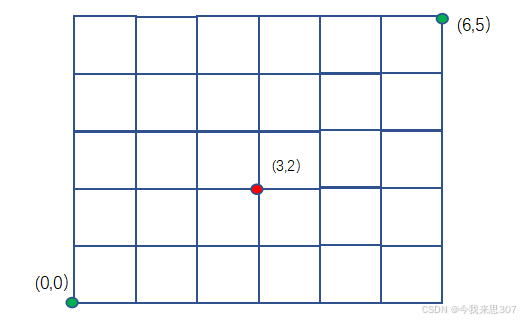
上图为从点(0,0)出发到点 (6,5)的示意图,要求每步只能沿着向上、下、左、右任意一个方向走一格长度。假设根据实际情况要求,存在一个点(3,2)必须通过。给定输入终点(m,n)坐标和必须通过的点(p,q),其中其中m,n,p,q都为自然数,点(p,q)不是起点也不是终点。
求从点(0,0)出发且经过点(p,q)到点(m,n)的最短路径的条数,并输出在所有最短路径中所经过点的纵坐标和最小的那一条路径。
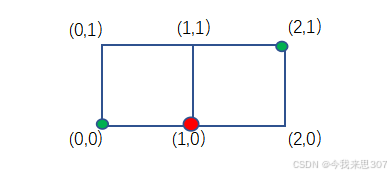
比如,在下图从点(0,0)到点(2,1)的所有路径中,点(1,0)必须通过,最短的路径有两条:
(0,0)->(1,0)->(2,0)->(2,1)和(0,0)->(1,0)->(1,1)->(2,1),其中所经过的点的纵坐标和最小的是(0,0)->(1,0)->(2,0)->(2,1)这条。
程序的输入有两行:第一行为终点坐标;第二行为必须通过的点的坐标
输出也有两行:第一行为最短路径的条数;第二行为在所有最短路径中,纵坐标的和最小的那一条路径。
比如:
输入:
2 1
1 0
输出:
2
(0,0)(1,0)(2,0)(2,1)
| 测试输入 | 期待的输出 | 时间限制 | 内存限制 | 额外进程 | |
|---|---|---|---|---|---|
| 测试用例 1 | 以文本方式显示
| 以文本方式显示
| 1秒 | 64M | 0 |