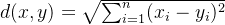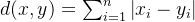【机器学习】自定义数据集，使用scikit-learn 中K均值包进行聚类

一、K 均值算法简介

K 均值算法的目标是将数据集划分为 K 个簇，使得每个数据点属于离它最近的簇中心（centroid）所代表的簇。

K均值聚类算法步骤

① 初始化：

随机选择原始数据的K个数据点作为初始质心（聚类中心）。

② 分配：

将每个数据点划分到距离最近的质心所对应的簇中，即计算每个数据点到每个质心的距离，选择距离最近的质心作为该数据点所属的簇。

③ 更新：

重新计算每个簇的质心，即将该簇中所有数据点的坐标取平均值，得到新的质心。

④ 迭代：

重复第②步和第③步，直到簇内的数据点相似度达到一定程度，或者达到预设的最大迭代次数。

二、`scikit-learn` 中的 `KMeans` 类

sklearn.cluster.KMeans 是 scikit-learn 中实现 K 均值算法的类。以下是它的主要参数和方法：

1. 主要参数

① `n_clusters`：

聚类的数量（K 值）。

默认值为 8。

② `init`：

初始化簇中心的方法。

可选值：'k-means++'（默认，一种智能初始化方法）或 'random'（随机初始化）。

③ `n_init`：

使用不同的初始簇中心运行算法的次数。

最终选择最优的结果（即簇内误差平方和最小的结果）。

默认值为 10。

④ `max_iter`：

单次运行算法的最大迭代次数。

默认值为 300。

⑤ `random_state`：

随机种子，用于确保结果可重复。

默认值为 None。

2. 主要属性

① `cluster_centers_`：

每个簇的中心坐标。

形状为 (n_clusters, n_features)。

② `labels_`：

每个样本的聚类标签。

形状为 (n_samples,)。

③ `inertia_`：

簇内误差平方和（SSE，Sum of Squared Errors），表示簇内数据点到簇中心的距离平方和。

越小表示聚类效果越好。

④ `n_iter_`：

实际运行的迭代次数。

3. 主要方法

① `fit(X)`：

训练模型，对输入数据 X 进行聚类。

X 是形状为 (n_samples, n_features) 的数组。

② `predict(X)`：

预测输入数据 X 的聚类标签。

返回形状为 (n_samples,) 的数组。

③ `fit_predict(X)`：

先调用 fit 训练模型，然后调用 predict 返回聚类标签。

④ `transform(X)`：

将输入数据 X 转换到簇中心距离空间。

返回形状为 (n_samples, n_clusters) 的数组，表示每个样本到每个簇中心的距离。

⑤ `score(X)`：

返回簇内误差平方和的相反数（即 -inertia_）。

4. 示例代码

以下是一个使用 KMeans 进行聚类的示例代码：

import numpy as np
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt

# 1. 自定义数据集
# 生成 200 个样本，每个样本有 2 个特征
np.random.seed(42)
X = np.random.randn(200, 2)

# 2. 初始化 K 均值模型
kmeans = KMeans(n_clusters=3, random_state=42)

# 3. 训练模型
kmeans.fit(X)

# 4. 获取聚类结果
labels = kmeans.labels_
centroids = kmeans.cluster_centers_

# 5. 可视化聚类结果
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis', s=50, alpha=0.8)
plt.scatter(centroids[:, 0], centroids[:, 1], c='red', marker='X', s=200, label='聚类中心')
plt.title("K均值聚类")
plt.xlabel("特征1")
plt.ylabel("特征2")
plt.legend()
plt.show()

三、数据点与聚类中心距离

1. 欧式距离（Euclidean Distance）

① 定义

欧式距离是两点之间的直线距离，计算公式为：

$d(x, y)=\sqrt{\sum_{i=1}^{n}(x_{i}-y_{i})^{2}}$

其中：

x 和 y 是两个数据点。

n 是特征的数量。

② 特点

适用于连续型数据。

对数据的尺度敏感，因此在使用前通常需要对数据进行标准化。

③ 在 K 均值中的使用

scikit-learn 的 KMeans 默认使用欧式距离。

无需额外设置。

④ 代码示例

import numpy as np
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt

# 1. 自定义数据集
np.random.seed(42)
X = np.random.randn(200, 2)

# 2. 初始化 K 均值模型（默认使用欧式距离）
kmeans = KMeans(n_clusters=3, random_state=42)

# 3. 训练模型
kmeans.fit(X)

# 4. 获取聚类结果
labels = kmeans.labels_
centroids = kmeans.cluster_centers_

# 5. 可视化聚类结果
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis', s=50, alpha=0.8)
plt.scatter(centroids[:, 0], centroids[:, 1], c='red', marker='X', s=200, label='聚类中心')
plt.title("K均值聚类（欧式距离）")
plt.xlabel("特征1")
plt.ylabel("特征2")
plt.legend()
plt.show()

2. 曼哈顿距离（Manhattan Distance）

① 定义

曼哈顿距离是两点在各维度上绝对差值的总和，计算公式为：

$d(x, y)=\sum_{i=1}^{n}\left |x_{i}-y_{i}\right |$

其中：

x 和 y 是两个数据点。

n 是特征的数量。

② 特点

适用于离散型数据或高维稀疏数据。

对异常值不敏感。

③ 在 K 均值中的使用

scikit-learn 的 KMeans 默认不支持曼哈顿距离。

可以通过自定义距离度量或使用其他库（如 scipy.spatial.distance）来实现。

④ 代码示例

import numpy as np
from scipy.spatial.distance import cdist
import matplotlib.pyplot as plt

# 1. 自定义数据集
np.random.seed(42)
X = np.random.randn(200, 2)

# 2. 自定义 K 均值算法（使用曼哈顿距离）
def kmeans_manhattan(X, n_clusters, max_iter=300, random_state=42):
    np.random.seed(random_state)
    # 随机初始化聚类中心
    centroids = X[np.random.choice(X.shape[0], n_clusters, replace=False)]
    
    for _ in range(max_iter):
        # 计算曼哈顿距离
        distances = cdist(X, centroids, metric='cityblock')
        # 分配样本到最近的簇
        labels = np.argmin(distances, axis=1)
        # 更新聚类中心
        new_centroids = np.array([X[labels == i].mean(axis=0) for i in range(n_clusters)])
        # 判断是否收敛
        if np.all(centroids == new_centroids):
            break
        centroids = new_centroids
    
    return labels, centroids

# 3. 训练模型
labels, centroids = kmeans_manhattan(X, n_clusters=3)

# 4. 可视化聚类结果
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis', s=50, alpha=0.8)
plt.scatter(centroids[:, 0], centroids[:, 1], c='red', marker='X', s=200, label='聚类中心')
plt.title("K均值聚类（曼哈顿距离）")
plt.xlabel("特征1")
plt.ylabel("特征2")
plt.legend()
plt.show()

四、自定义数据集，使用scikit-learn 中K均值包进行聚类

1. 代码示例

import numpy as np
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt

# 1. 自定义数据集
# 生成 200 个样本，每个样本有 2 个特征
np.random.seed(42)  # 设置随机种子以确保结果可重复
X = np.random.randn(200, 2).astype(np.float32)

# 2. 初始化 K 均值模型
# 设置聚类数为 3
kmeans = KMeans(n_clusters=3, random_state=42)

# 3. 训练模型
kmeans.fit(X)

# 4. 获取聚类结果
# 获取每个样本的聚类标签
labels = kmeans.labels_
# 获取聚类中心
centroids = kmeans.cluster_centers_

# 5. 可视化聚类结果
# 绘制样本点，按聚类标签着色
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis', s=50, alpha=0.8)
# 绘制聚类中心
plt.scatter(centroids[:, 0], centroids[:, 1], c='red', marker='X', s=200, label='聚类中心')
plt.title("K均值聚类")
plt.xlabel("特征1")
plt.ylabel("特征2")
plt.legend()
plt.show()

2. 代码解释

① 自定义数据集：

X = np.random.randn(200, 2).astype(np.float32)：

生成 200 个样本，每个样本有 2 个特征。

使用 np.random.randn 生成符合标准正态分布的随机数。

astype(np.float32) 将数据类型转换为 32 位浮点数。

np.random.seed(42)：

设置随机种子，确保每次运行代码时生成的数据集相同。

② 初始化 K 均值模型：

kmeans = KMeans(n_clusters=3, random_state=42)：

使用 KMeans 初始化 K 均值模型。

n_clusters=3 表示将数据分为 3 个簇。

random_state=42 确保每次运行代码时聚类结果一致。

这里默认使用了欧式距离

③ 训练模型：

kmeans.fit(X)：

使用数据集训练 K 均值模型。

模型会计算每个样本的聚类标签和聚类中心。

④ 获取聚类结果：

labels = kmeans.labels_：

获取每个样本的聚类标签（0、1 或 2）。

centroids = kmeans.cluster_centers_：

获取每个簇的中心点。

⑤ 使用 `matplotlib` 绘制聚类结果：

plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis', s=50, alpha=0.8)：

绘制样本点，按聚类标签着色。

cmap='viridis' 指定颜色映射。

s=50 设置点的大小。

alpha=0.8 设置点的透明度。

plt.scatter(centroids[:, 0], centroids[:, 1], c='red', marker='X', s=200, label='Centroids')：

绘制聚类中心，用红色 X 标记。

s=200 设置标记的大小。

label=聚类中心' 添加图例标签。

plt.title("K均值聚类")：设置图表标题。
plt.xlabel(特征1"") 和 plt.ylabel("特征2")：设置坐标轴标签。
plt.legend()：显示图例。
plt.show()：显示图表。