0 前言
著名学者Julier等提出近似非线性函数的均值和方差远比近似非线性函数本身更容易,因此提出了基于确定性采样的UKF算法。
该算法的核心思想是:采用UT变换,利用一组Sigma采样点来描述随机变量的高斯分布,然后通过非线性函数的传递,再利用加权统计线性回归技术来近似非x线性函数的后验均值和方差。
相比于EKF,UKF的估计精度能够达到泰勒级数展开的二阶精度。
1 UT变换
2 采样策略
根据Sigma点采样策略不同,相应的Sigma点以及均值权值和方差权值也不尽相同,因此UT变换的估计精度也会有差异,但总体来说,其估计精度能够达到泰勒级数展开的二阶精度。
为保证随机变量x经过采样之后得到的Sigma采样点仍具有原变量的必要特性,所以采样点的选取应满足:
下面介绍两种常用的策略:比例采样和比例修正对称采样:
比例采样:
比例修正对称采样:
高斯白噪声非线性系统:
3 UKF算法流程
4 另一种UKF算法流程
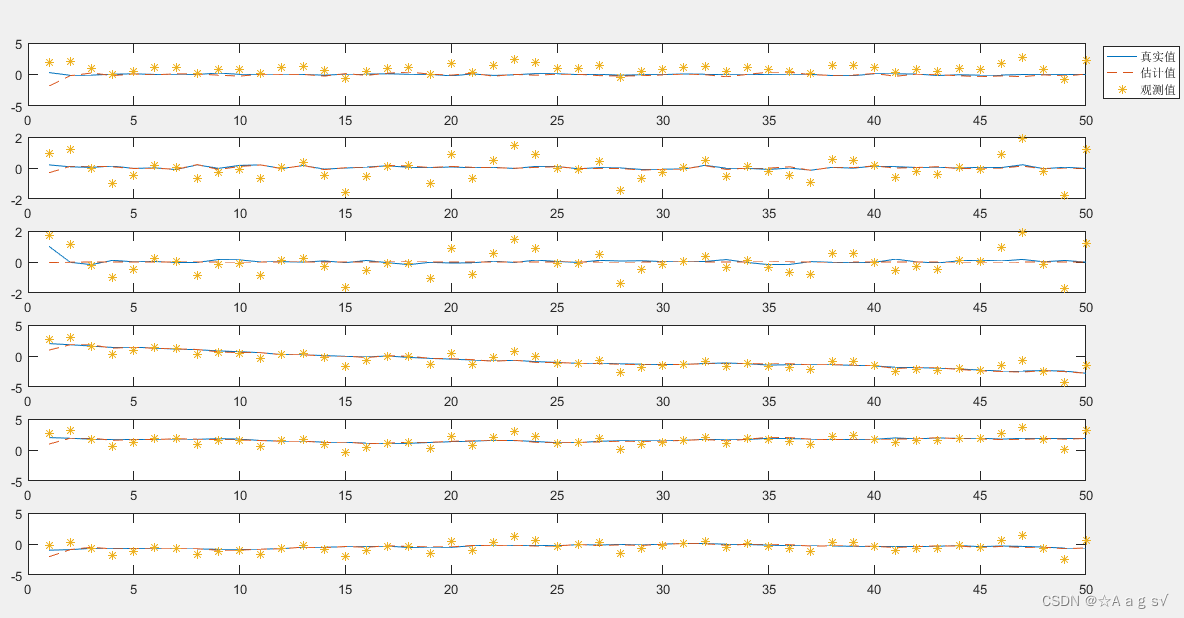
5 UKF算法仿真
clc;close all;clear all;
rng(4); % 固定随机种子
n=6; % 6维
t=0.2;
q=0.1; %std of process
r=0.7; %std of measurement
Q=q^2*eye(n); % covariance of process
R=r^2; % covariance of measurement
f=@(x)[x(1)*x(2);t*x(3);0.05*x(1)*t*(x(2)+x(3));x(4)+t*x(6);x(5);x(6)]; % nonlinear state equations
%f=@(x)[x(1)+t*x(3);x(2)+t*x(4);x(3)+t*x(5);x(4)+t*x(6);x(5);x(6)]; % nonlinear state equations
h=@(x)[sqrt(x(1)+1);0.8*x(2)+0.3*x(1);x(3);x(4);x(5);x(6)]; % measurement equation
s=[0.3;0.2;1;2;2;-1]; % initial state
x=s+q*randn(n,1); %initial state % initial state with noise
P = eye(n); % initial state covraiance
N=50; % total dynamic steps
xV = zeros(n,N); %estmate % allocate memory
sV = zeros(n,N); %actual
zV = zeros(n,N);
for k=1:N
z = h(s) + r*randn; % measurments 广播
zV(:,k) = z; % save measurment
sV(:,k)= s; % save actual state
s = f(s) + q*randn(n,1); % update process
[x, P] = ukf(f,x,P,h,z,Q,R); % ukf
xV(:,k) = x; % save estimate
end
for k=1:n % plot results
subplot(n,1,k)
plot(1:N, sV(k,:), '-', 1:N, xV(k,:), '--',1:N,zV(k,:),'*')
end
function [y,Y,P,Y1] = ut(f,X,Wm,Wc,n,Q)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Unscented Transformation
% UT转换函数
% Input:
% f: nonlinear map 跑观测方程是h
% X: sigma points
% Wm: weights for mean
% Wc: weights for covraiance
% n: numer of outputs of f
% Q: additive covariance 跑观测方程是R
% Output:
% y: transformed mean
% Y: transformed smapling points
% P: transformed covariance
% Y1: transformed deviations(偏差)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
L = size(X,2);
y = zeros(n,1);
Y = zeros(n,L);
for k=1:L
Y(:,k) = f(X(:,k));
y = y+Wm(k)*Y(:,k);
end
Y1 = Y-y(:,ones(1,L)); % 广播
P = Y1*diag(Wc)*Y1'+Q;
end
function [x,P] = ukf(f_func, x, P, h_func, z, Q, R)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% UKF Unscented Kalman Filter for nonlinear dynamic systems
% 无损卡尔曼滤波(Unscented Kalman Filter)函数,适用于动态非线性系统
% for nonlinear dynamic system (noises are assumed as additive):
% x_k+1 = f(x_k) + w_k
% z_k = h(x_k) + v_k
% w ~ N(0,Q) meaning w is gaussian noise with covariance Q
% v ~ N(0,R) meaning v is gaussian noise with covariance R
% =============================参数说明=================================
% Inputs:
% fstate -[function]: 状态方程f(x)
% x - [vec]: 状态先验估计 "a priori" state estimate
% P - [mat]: 方差先验估计 "a priori" estimated state covariance
% hmeas -[function]: 量测方程h(x)
% z - [vec]: 量测数据 current measurement
% Q - [mat]: 状态方程噪声w(t) process noise covariance
% R - [mat]: 量测方程噪声v(t) measurement noise covariance
% Output:
% x - [mat]: 状态后验估计 "a posteriori" state estimate
% P - [mat]: 方差后验估计 "a posteriori" state covariance
% =====================================================================
% By Yi Cao at Cranfield University, 04/01/2008
% Modified by JD Liu 2010-4-20
% Modified by zhangwenyu, 12/23/2013
% Modified by yangkunfeng, 2022-8-23
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
if nargin<7
error('Not enough inputarguments!');
end
% 初始化,为了简化函数,求lamda的过程被默认
n_x = numel(x); %numer of states
n_z = numel(z); %numer of measurements
alpha = 1e-3; %default, tunable
kappa = 0; %default, tunable
beta = 2; %default, tunable
% UT转换部分
lambda = alpha^2*(n_x+kappa)-n_x; %scaling factor
c = n_x+lambda; %scaling factor
Wm = [lambda/c 0.5/c+zeros(1,2*n_x)]; %weights for means 广播
Wc = Wm;
Wc(1) = Wc(1)+(1-alpha^2+beta); %weights for covariance
X = sigmas(x,P,c); %sigma points around x
[x1,X1,P_X1,err_X1] = ut(f_func,X,Wm,Wc,n_x,Q);%unscented transformation of process
% X1=sigmas(x1,P_X1,c); %sigma points around x1
% X2=X1-x1(:,ones(1,size(X1,2))); %deviation of X1
[z1,Z1,P_Z1,err_Z1] = ut(h_func,X1,Wm,Wc,n_z,R);%unscented transformation of measurments
% 滤波部分
P_X1_Z1 = err_X1*diag(Wc)*err_Z1'; %transformed cross-covariance %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
K = P_X1_Z1*inv(P_Z1); % 计算增益
x = x1+K*(z-z1); %state update x1是ut变换之后状态的先验
P = P_X1-K*P_X1_Z1'; % P = P_X1-K*P_Z1*K' %covariance update P1是ut变换之后状态和状态先验,P是后验
end
function X = sigmas(x,P,c)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Sigma points around reference point
% 构造2n+1个sigma点
% Inputs:
% x: reference point
% P: covariance
% c: coefficient
% Output:
% X: Sigma points
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
A = sqrt(c)*chol(P)';
Y = x(:,ones(1,numel(x)));
X = [x Y+A Y-A];
end
仿真结果