前言
前面我们通过堆实现了二叉树,接下来我们用链表实现二叉树。
1. 实现链式结构二叉树
1.1 结构体定义
二叉树的每个结点需要两个指针,分别指向其左孩子和右孩子。还有一个结点域,存储数据。
还是将数据类型重命名,便于后面更改。一个结构体指针指向左孩子,另一个指向右孩子。
1.2 申请结点
由于二叉树的结点都是动态申请的,需要多次,因此我们将它封装为函数便于使用。
先动态申请结点大小的内存,然后判断是否为空,不为空则对其进行初始化,一开始将左右指针都指向空,将数据赋值,最后返回新结点。
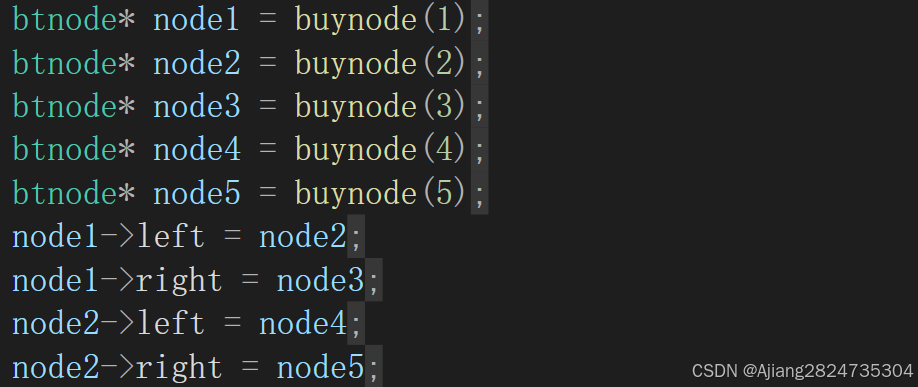
1.3 二叉树构建
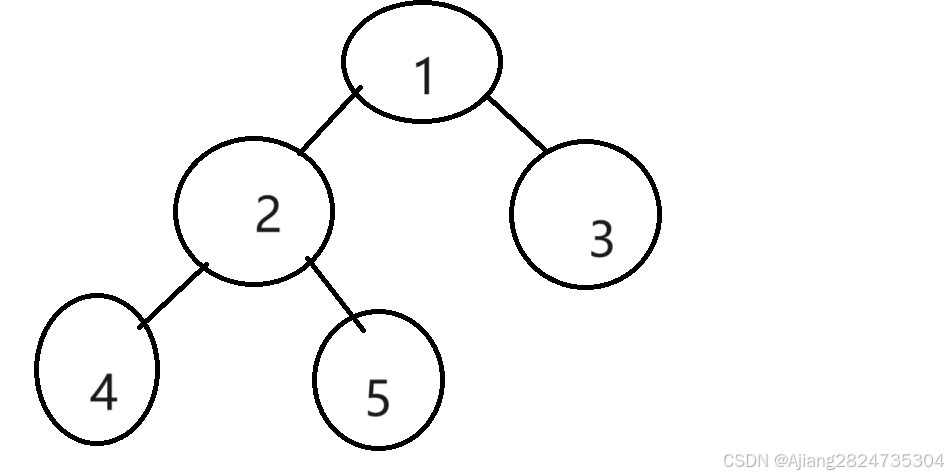
通过如上代码,我们现实了一个简单二叉树。二叉树如下图:
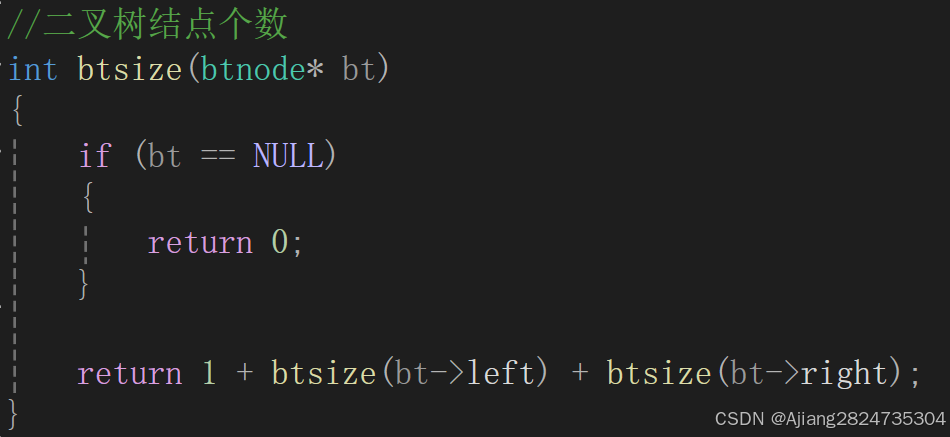
1.4 求二叉树结点个数
我们通过递归的方式求结点个数,二叉树的很多功能都是用递归实现,二叉树就是关于递归的暴力美学。
如果结点为空,则返回0停止递归,否则就进行递归,返回本身的结点树和左子树的结点数以及右子树的结点数。
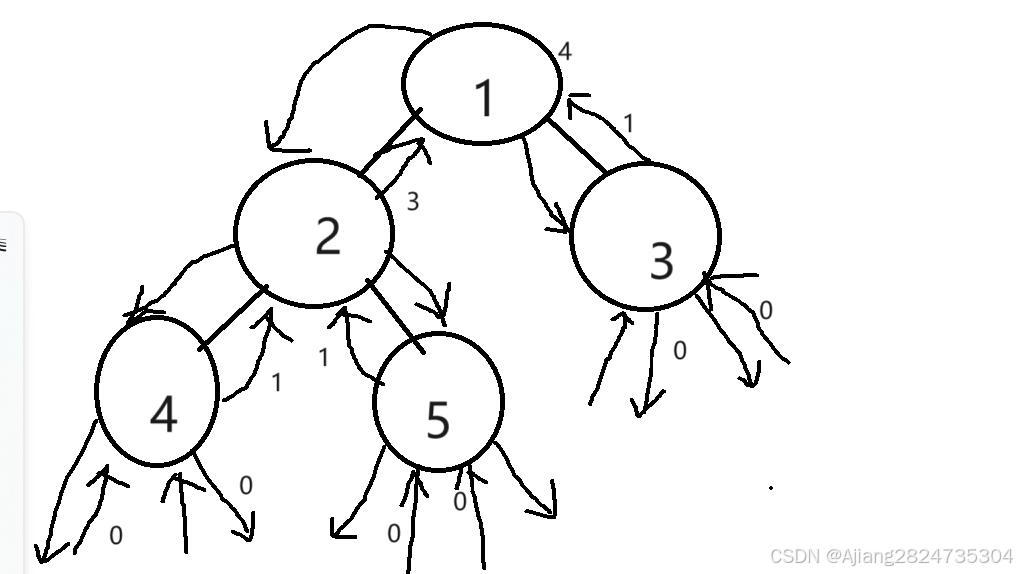
分析:当传入第一个结点的时候,结点不为空,则进入递归,到一号结点的左节点及二号结点,该结点不为空,进入递归,到四号结点,四号结点不为空,进入递归,而四号结点的左子树为空,返回0,然后进入四号结点的右子树,也返回0。然后到四号结点,返回1。再到二号结点的右子树,跟四号结点是一种情况,返回1。再到二号结点,返回3。再到三号结点,与四号结点类似,返回1,最后到一号结点,返回5。
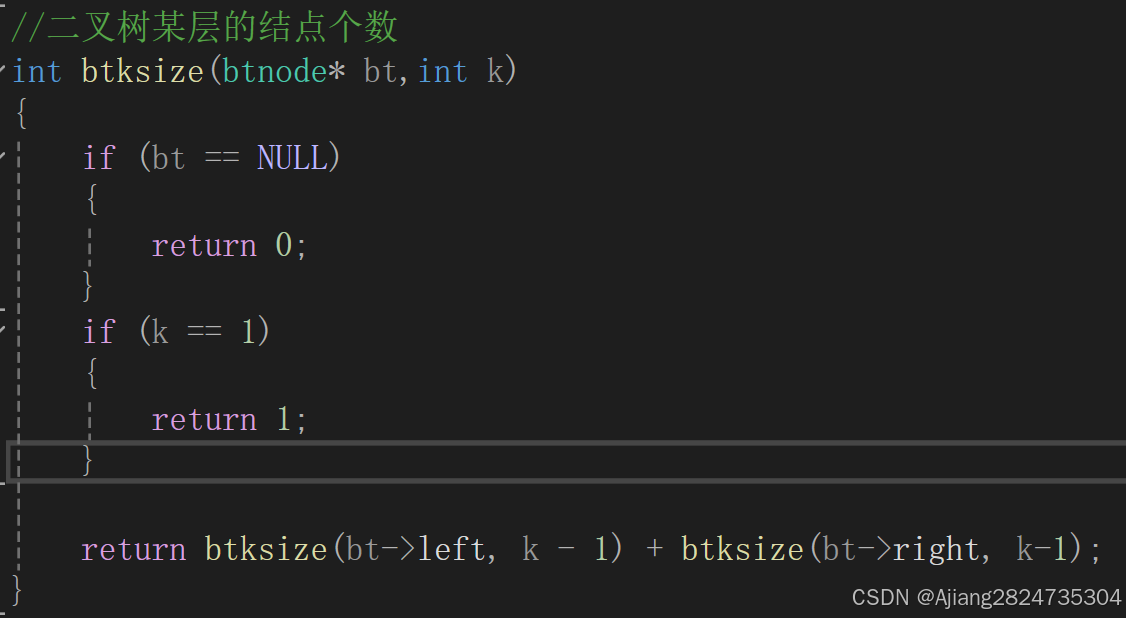
1.5 求某层结点的个数
我们知道了某层的层次k,就可以通过一个if循环来判断该结点个数。
k表示第几层,当k不为1时不进行计数,只有当k为1时才进行记录个数。返回的是该结点的左子树和右子树在k层的结点个数。如果没达到k层就为空了,则不计数。
1.6 求叶子结点个数
叶子结点的特征就是左子树和右子树都为NULL,所以如果遇到这样的结点则计数,否则不计数。
 1.7 查找值为x的结点
1.7 查找值为x的结点
递归结点的左右子树,如果碰到值相等的则返回这个结点,如果一直没遇到则返回空。
通过if递归左右子树。
1.8 求二叉树的层次
我们知道,如果是完全二叉树,则左子树层次一定比右子树的层次深。所以我们递归左子树就可以了。
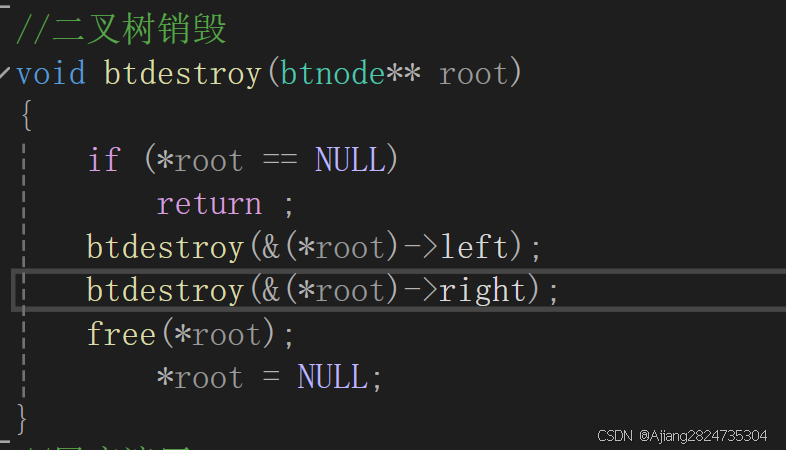
1.9 二叉树销毁
遍历二叉树,将每个结点都置free并置为空。因为要遍历二叉树,所以不能从根结点开始销毁,如果销毁了就找不到其他的结点了。
因为会销毁头结点,所以需要用到二级指针。
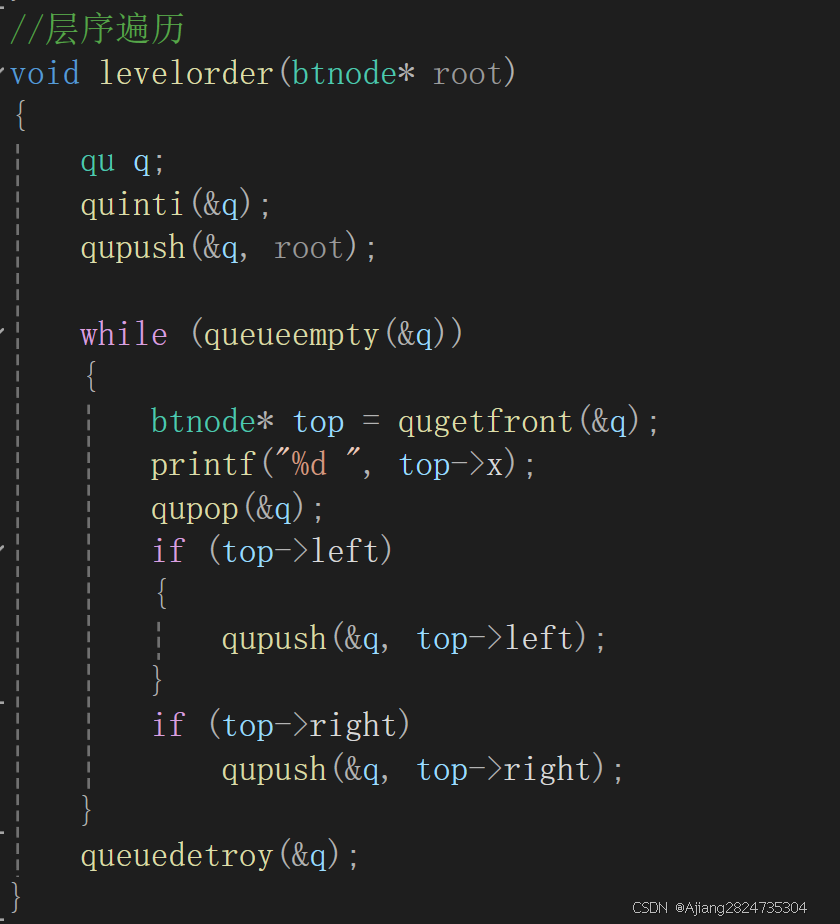
1.10 二叉树层次遍历
层次遍历需要通过队列来实现。
思路:将根结点放入队列中,然后将根结点取出并打印,将根结点的左右不为空的结点放入队列,再依次取出并打印,再放入其左右非空结点。直到队列为空。
这里需要注意,由于需要用到队列,我们需要创建并初始化队列,最后将队列进行销毁。
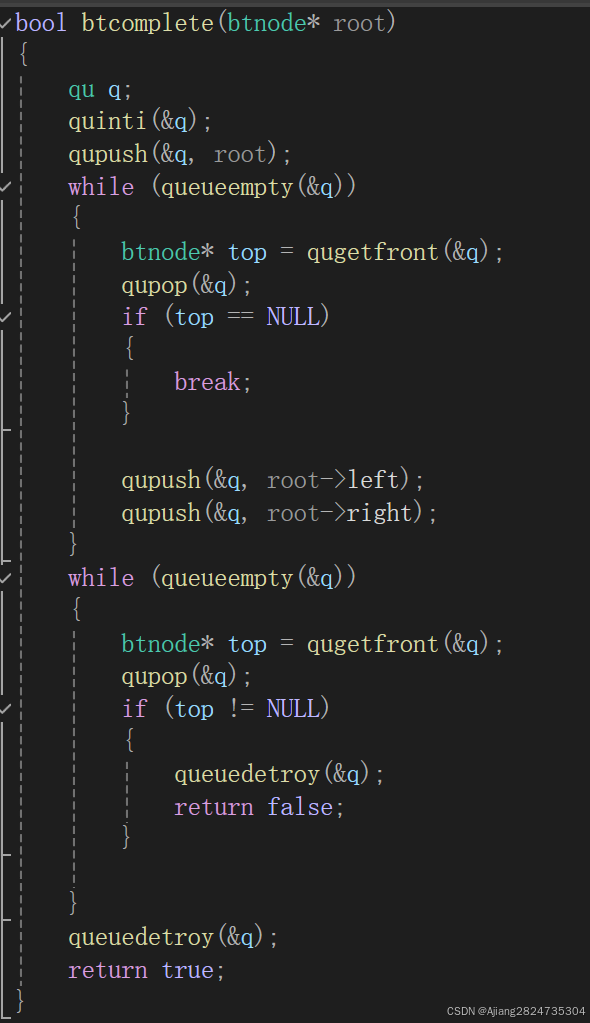
1.11 判断是否为完全二叉树
判断完全二叉树也需要队列进行判断。
思路:跟层次遍历一样,需要通过反复的取出结点并放入子结点,但不同的是,除非结点为空,否则其左右结点都需要放入队列。当取出到空结点的时候便不再进行取放操作,然后判断队列元素是否全为空,如果为空则是完全二叉树,如果不为空就不是完全二叉树。
注意:在返回false的时候也需要销毁队列。
2. oj题
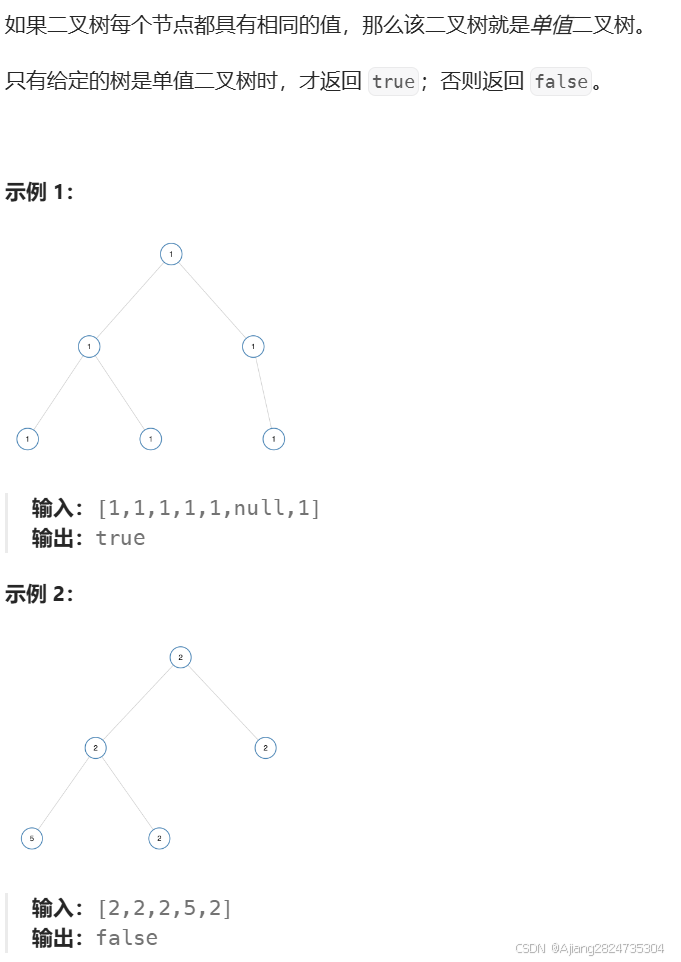
2.1 单值二叉树
思路:如果根结点的左右子树与根结点的值相同,那么左右子树就可以单独再与其左右子树进行判断,进行递归。
注意:当递归到空结点的时候,这个时候返回true,因为空结点不影响结果。
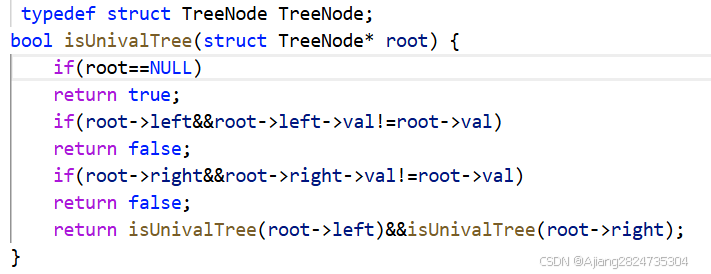
如果遇到一个不相同的值便可以返回false了,最后将根结点的左右子树结果进行&&操作,只有两个子树都为true时这棵树才是单值二叉树。
代码如下:
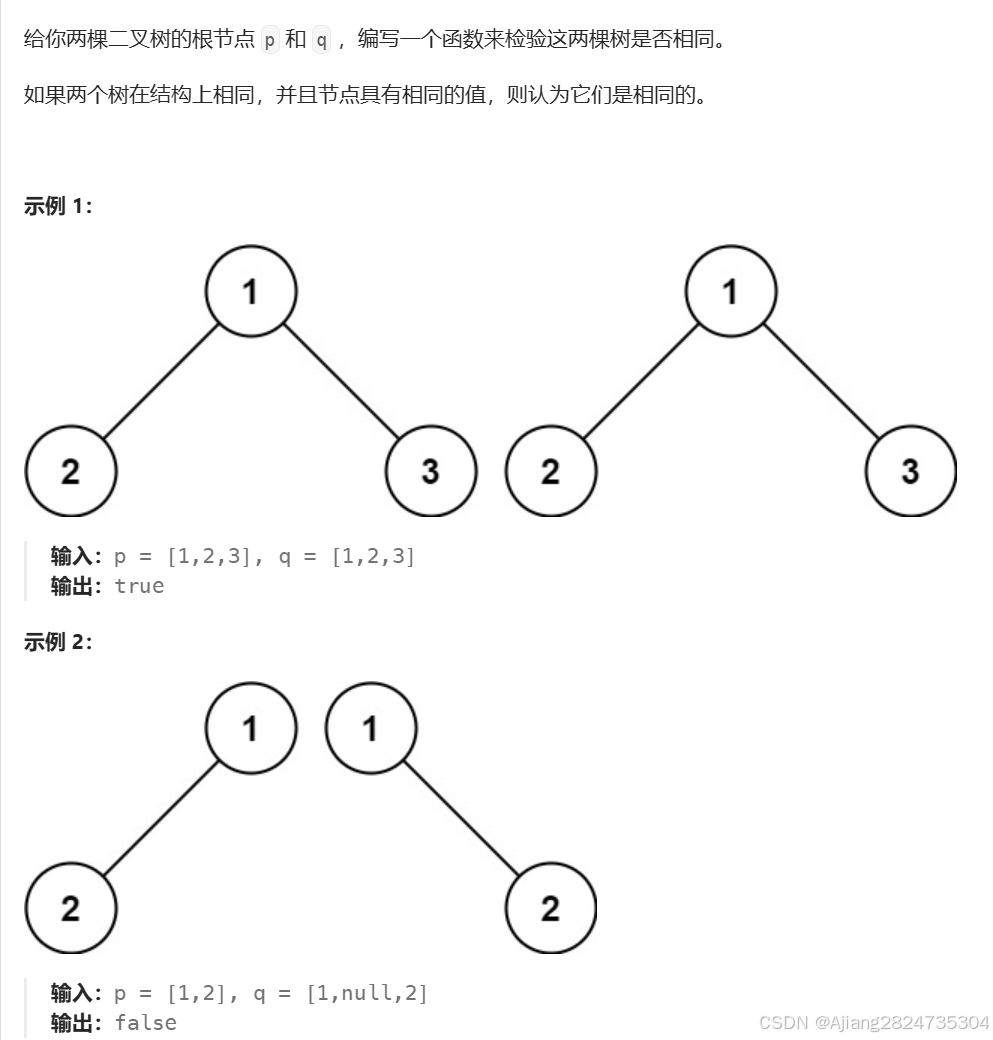
2.2 检查两颗二叉树是否相同
思路:判断两个二叉树的头结点是否相同,如果相同则进行左右子树递归,不同则返回false,相同则不管,最后当空结点的时候返回true。
注意:当两颗二叉树都为空,是相同二叉树,当只有其中一颗为空时则不相同。
代码如下:
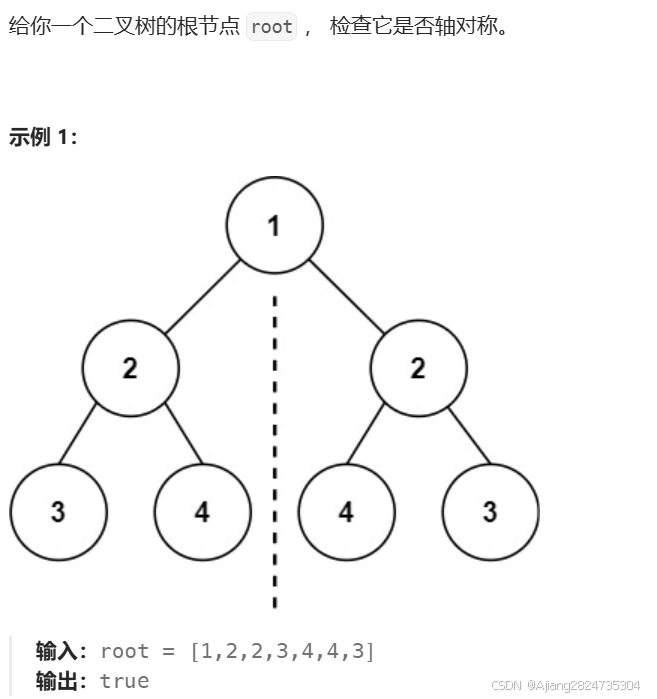
2.3 轴对称树
思路:可以借助上一题实现的相同树,只需要稍微修改,即将根结点的左子树与右子树进行判断是否相等。
代码如下:
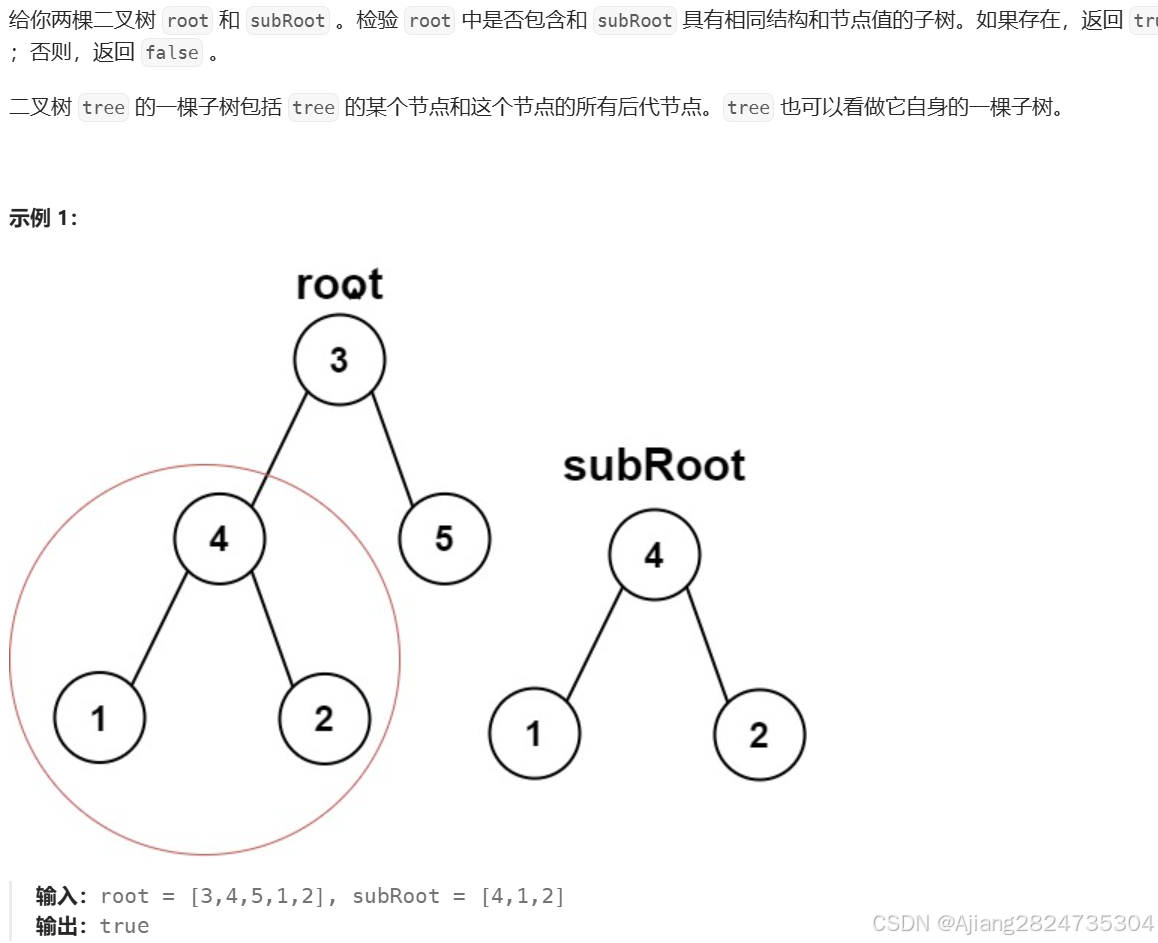
2.4 另一棵树的子树
思路:还是借助相同树。从头结点开始判断两棵树是否相同,然后遍历所有结点,只要有一颗树相同就行。
注意:递归的时候return是使用 || 。
代码如下:
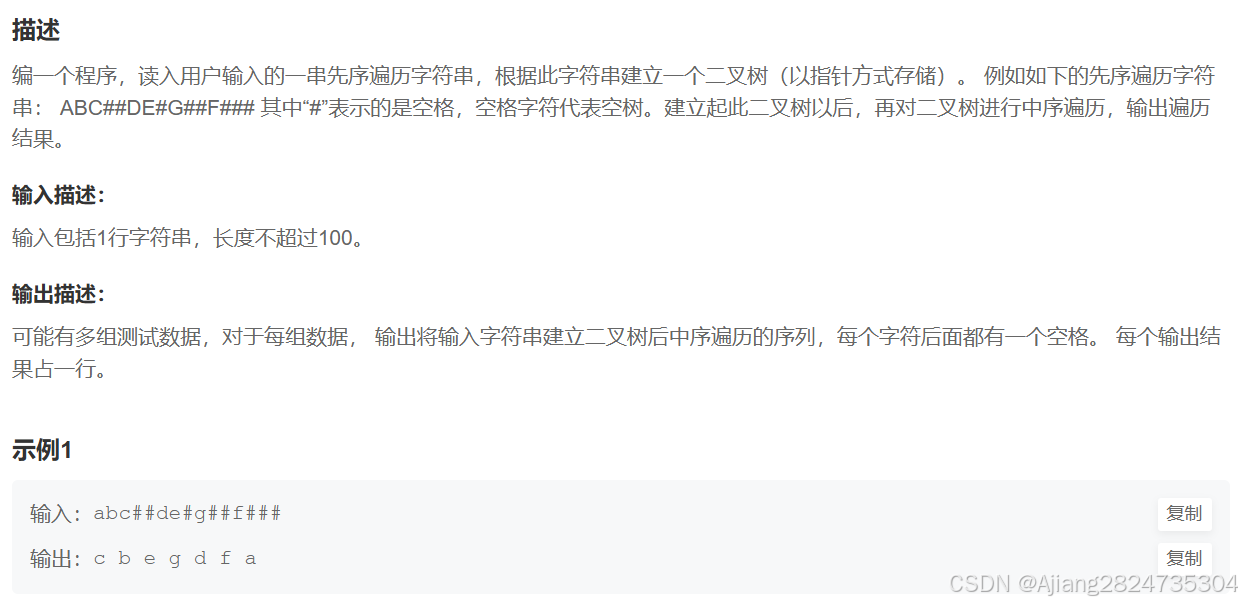
2.5 二叉树的构建即遍历
思路:通过递归进行构建二叉树。因为给先序遍历,即“根左右”。因此第一个是根结点,第二个是根结点的左结点,也是左子树的根结点。如果再读到一个不为空的值,那肯定是第二个结点的左结点,依次下去。直到读到两个为空的符号时这个结点便结束了,返回这个结点的根结点,再进行该根结点的右子树的创建,但是需要注意根结点的创建也是从左子树开始创建的。当读到一个为空的符号时,代表该结点的左子树结束,创建该结点的右子树。
因此递归的终止条件是读到为空的符号。
代码如下:
#include <stdio.h>
#include <stdlib.h>
//1.
typedef char btdatatype;
typedef struct btnode{
struct btnode * left ;
struct btnode* right;
btdatatype val;
}btnode;
btnode * buynode(char x)
{
btnode * newnode = (btnode *)malloc(sizeof(btnode));
newnode->val =x;
newnode->left = newnode->right = NULL;
return newnode;
}
btnode * create(char * arr,int * pi)
{
if(arr[*pi]=='#')
{++(*pi);
return NULL;}
btnode * root = buynode(arr[*pi]);
++(*pi);
root->left = create(arr,pi);
root->right= create(arr,pi);
return root;
}
void inorder(btnode * root)
{
if(root==NULL)
return ;
inorder(root->left);
printf("%c ",root->val);
inorder(root->right);
}
int main() {
char arr[100];
scanf("%s ",arr);
int i =0;
btnode * root = create(arr,&i);
inorder(root);
return 0;
}
具体实现的时候需要申请结点以及进行中序遍历,中序遍历比较简单,这里就不讲了。
3.源码
二叉树的实现以及判断完全二叉树,层次遍历 · a36cc5b · 重邮阿江/c_study_experience - Gitee.com二叉树oj题 · 7452d90 · 重邮阿江/c_study_experience - Gitee.com