SCI一区级 | Matlab实现KOA-CNN-BiLSTM-Mutilhead-Attention开普勒算法优化卷积双向长短期记忆神经网络融合多头注意力机制多变量多步时间序列预测
目录
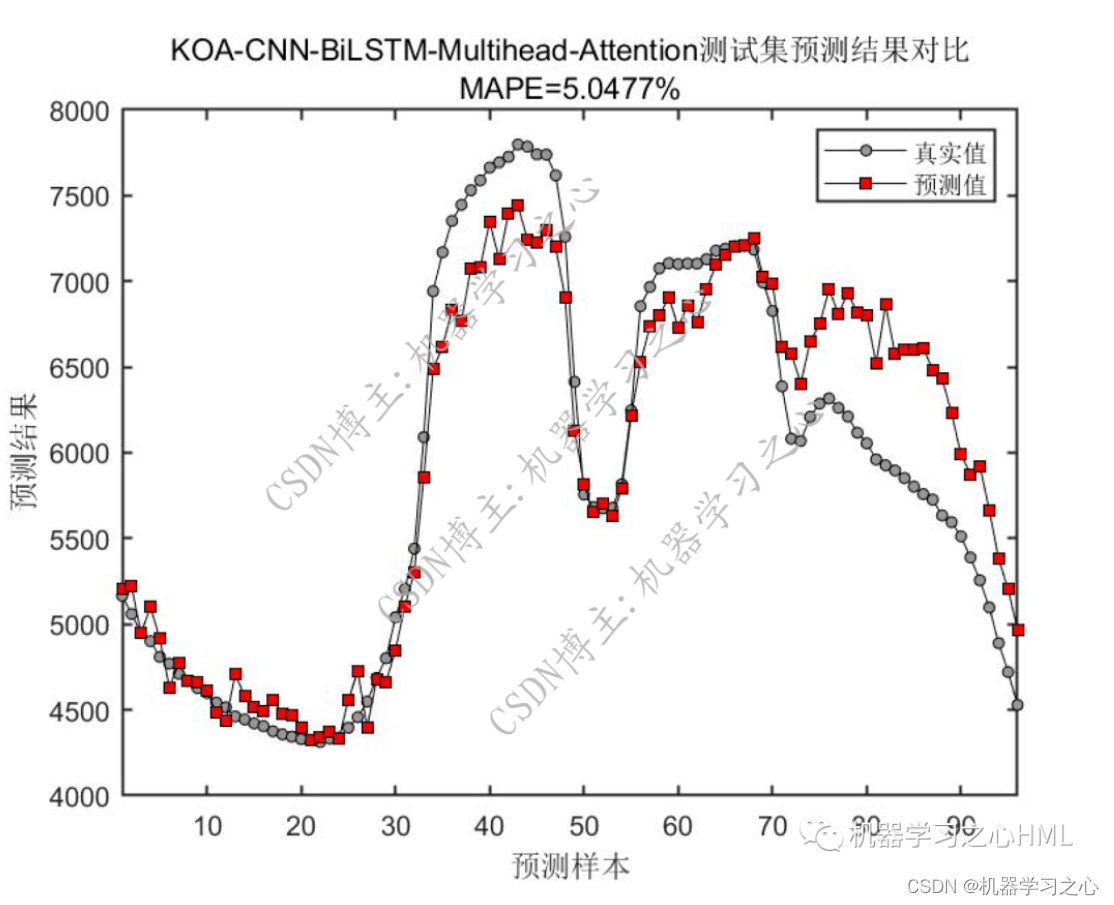
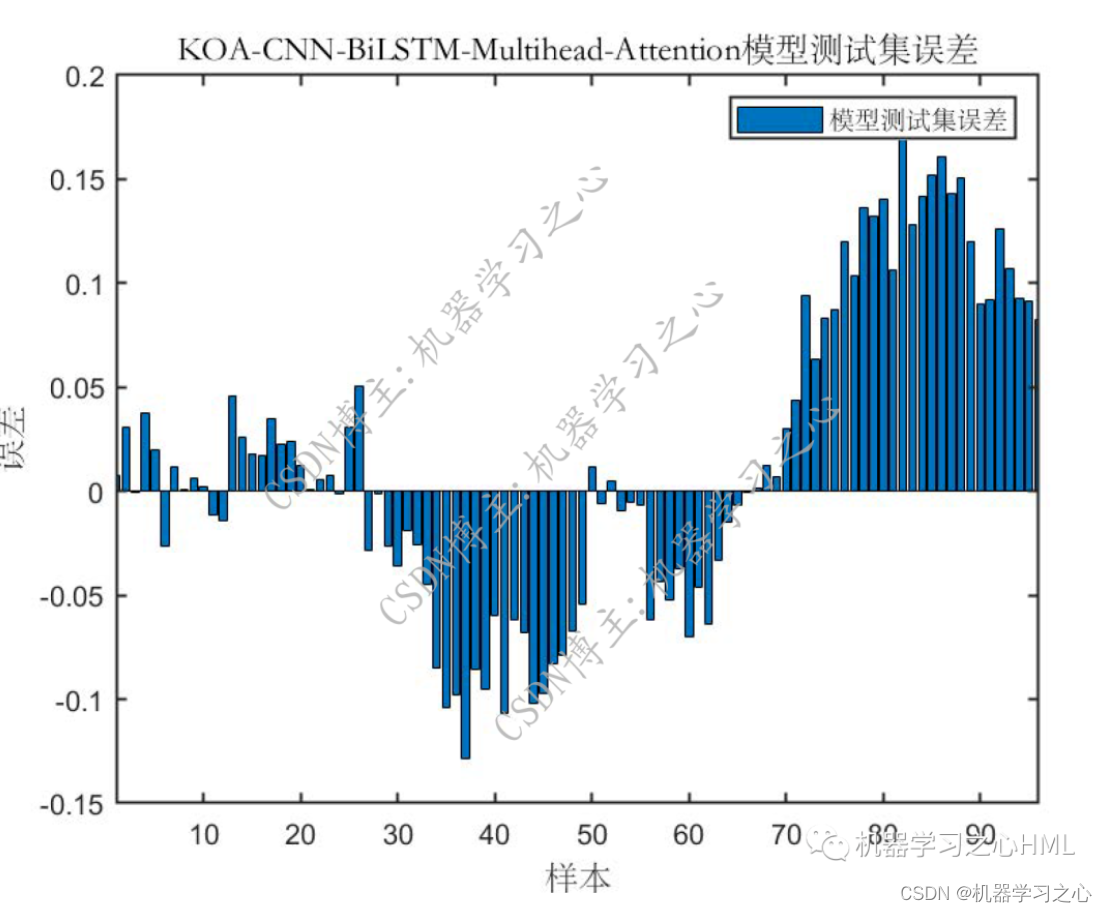
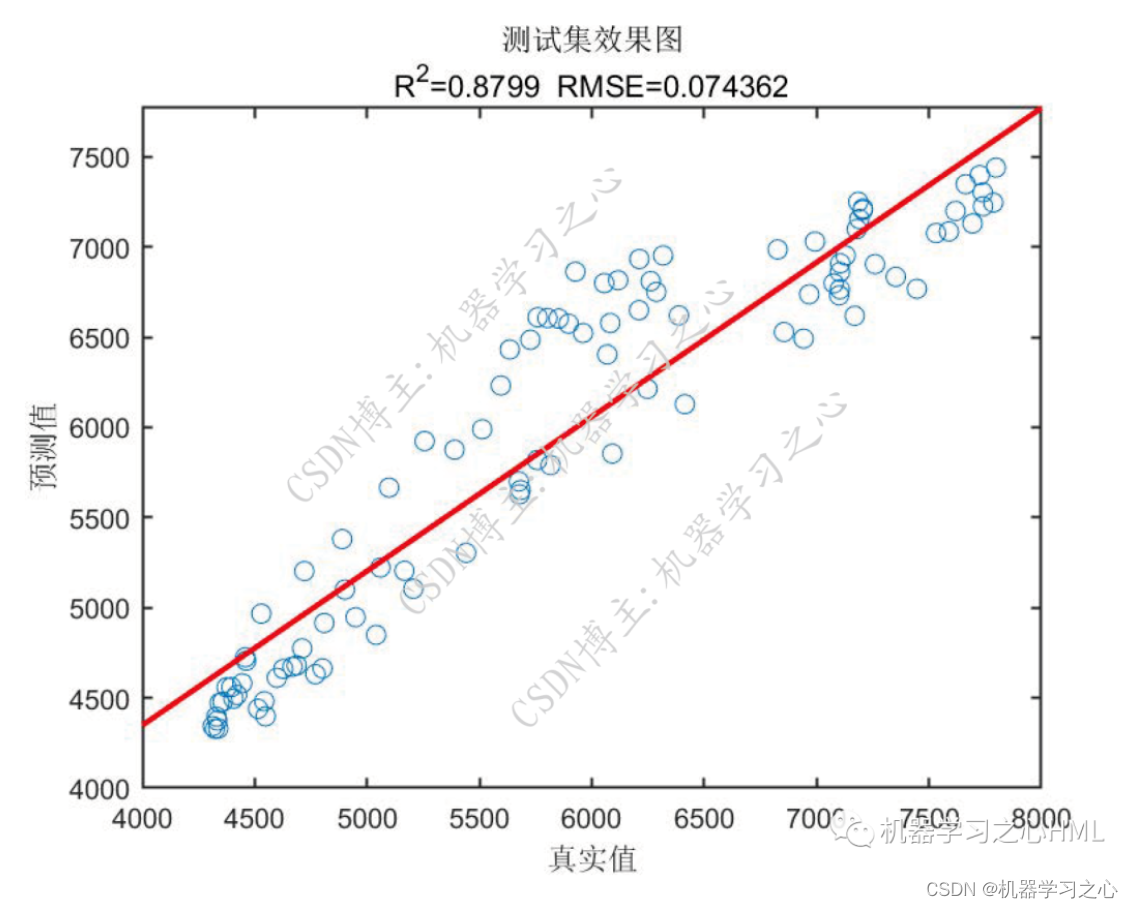
预测效果
基本介绍
1.Matlab实现KOA-CNN-BiLSTM-Mutilhead-Attention开普勒算法优化卷积双向长短期记忆神经网络融合多头注意力机制多变量多步时间序列预测,开普勒算法优化学习率,卷积核大小,神经元个数,以最小MAPE为目标函数;
CNN卷积核大小:卷积核大小决定了CNN网络的感受野,即每个卷积层可以捕获的特征的空间范围。选择不同大小的卷积核可以影响模型的特征提取能力。较小的卷积核可以捕获更细粒度的特征,而较大的卷积核可以捕获更宏观的特征。
BiLSTM神经元个数:BiLSTM是一种适用于序列数据的循环神经网络,其神经元个数决定了模型的复杂性和记忆能力。较多的BiLSTM神经元可以提高模型的学习能力,但可能导致过拟合。
学习率:学习率是训练深度学习模型时的一个关键超参数,它控制每次参数更新的步长。学习率过大可能导致模型不稳定和发散,学习率过小可能导致训练过慢或陷入局部最小值。
多头自注意力层 (Multihead-Self-Attention):Multihead-Self-Attention多头注意力机制是一种用于模型关注输入序列中不同位置相关性的机制。它通过计算每个位置与其他位置之间的注意力权重,进而对输入序列进行加权求和。注意力能够帮助模型在处理序列数据时,对不同位置的信息进行适当的加权,从而更好地捕捉序列中的关键信息。在时序预测任务中,注意力机制可以用于对序列中不同时间步之间的相关性进行建模。
开普勒优化算法(Kepler optimization algorithm,KOA)由Mohamed Abdel-Basset等人于2023年提出的一种基于物理学的元启发式算法,于2023年5月发表在SCI、中科院1区Top顶级期刊《Knowledge-Based Systems》上,它受到开普勒行星运动定律的启发,可以预测行星在任何给定时间的位置和速度。在KOA中,每个行星及其位置都是一个候选解,它在优化过程中随机更新,相对于迄今为止最优解。
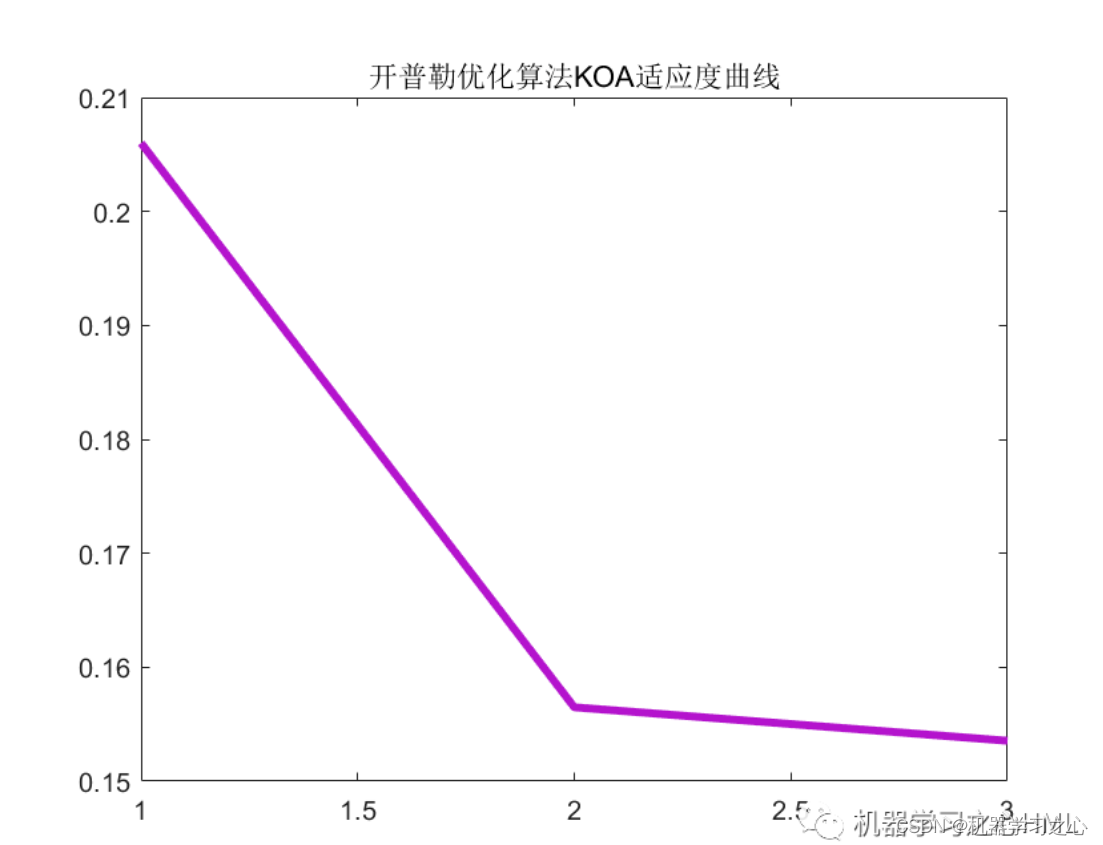
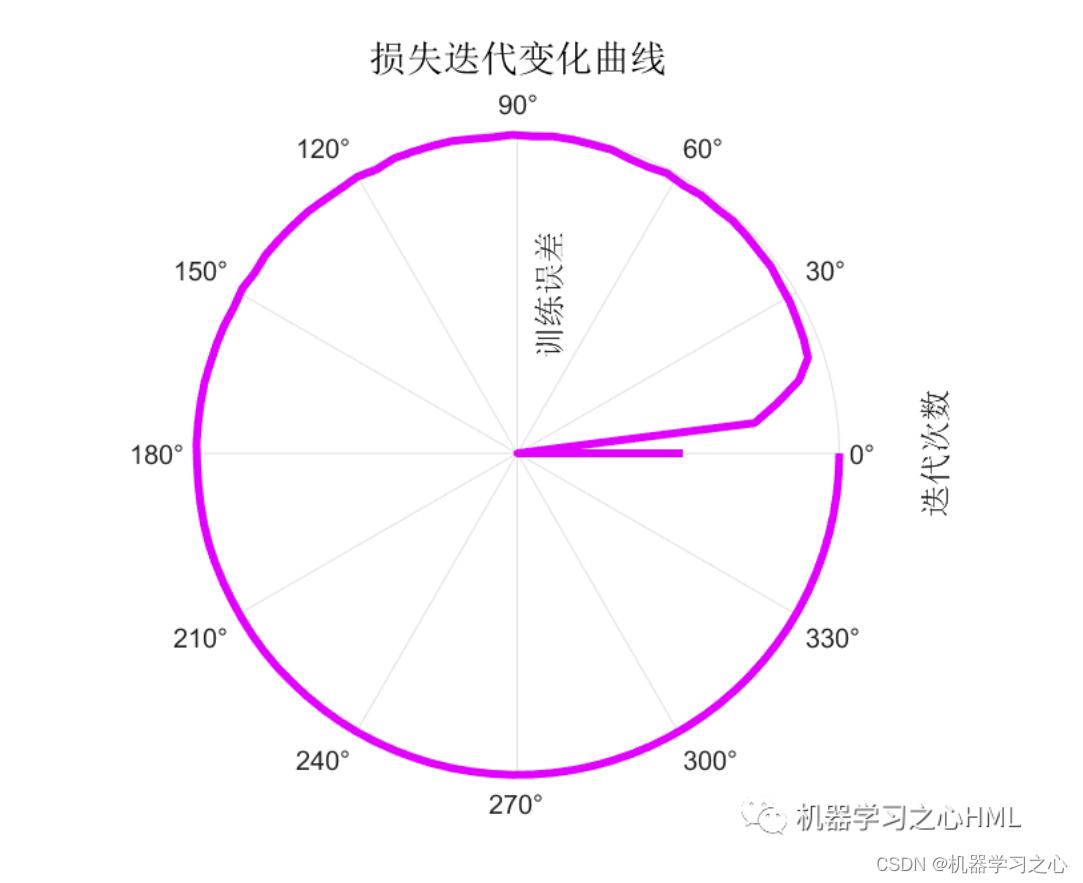
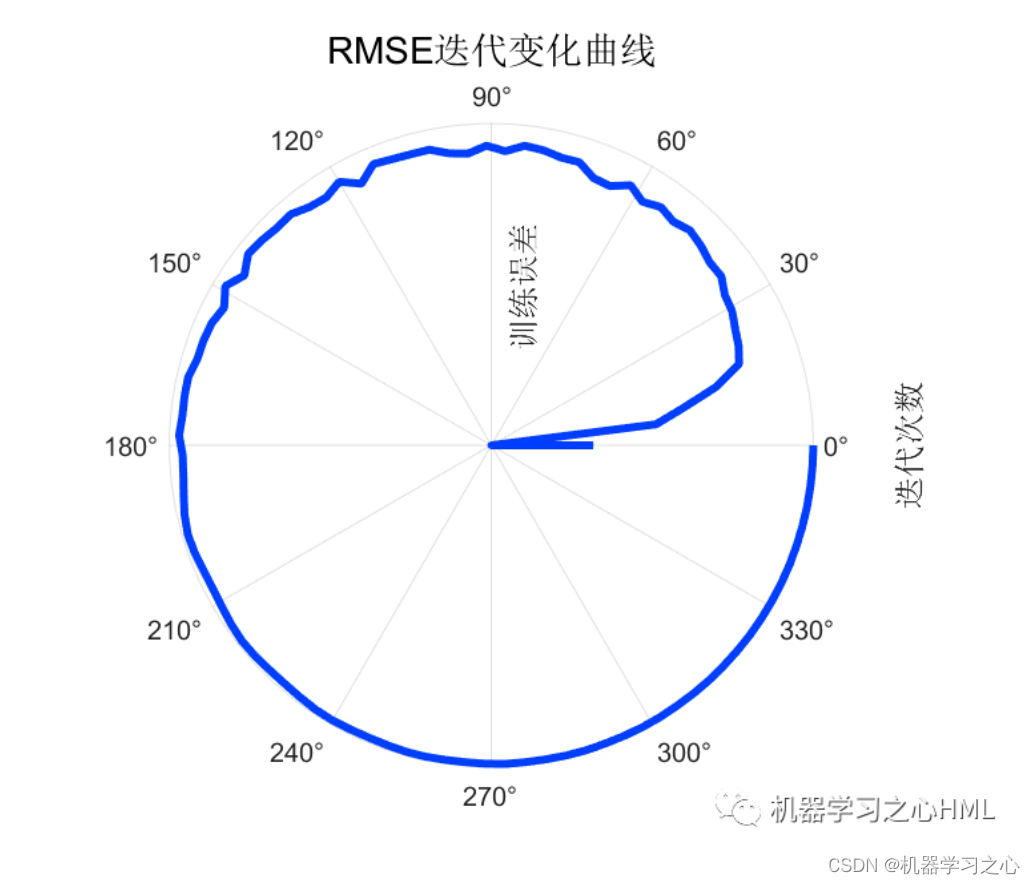
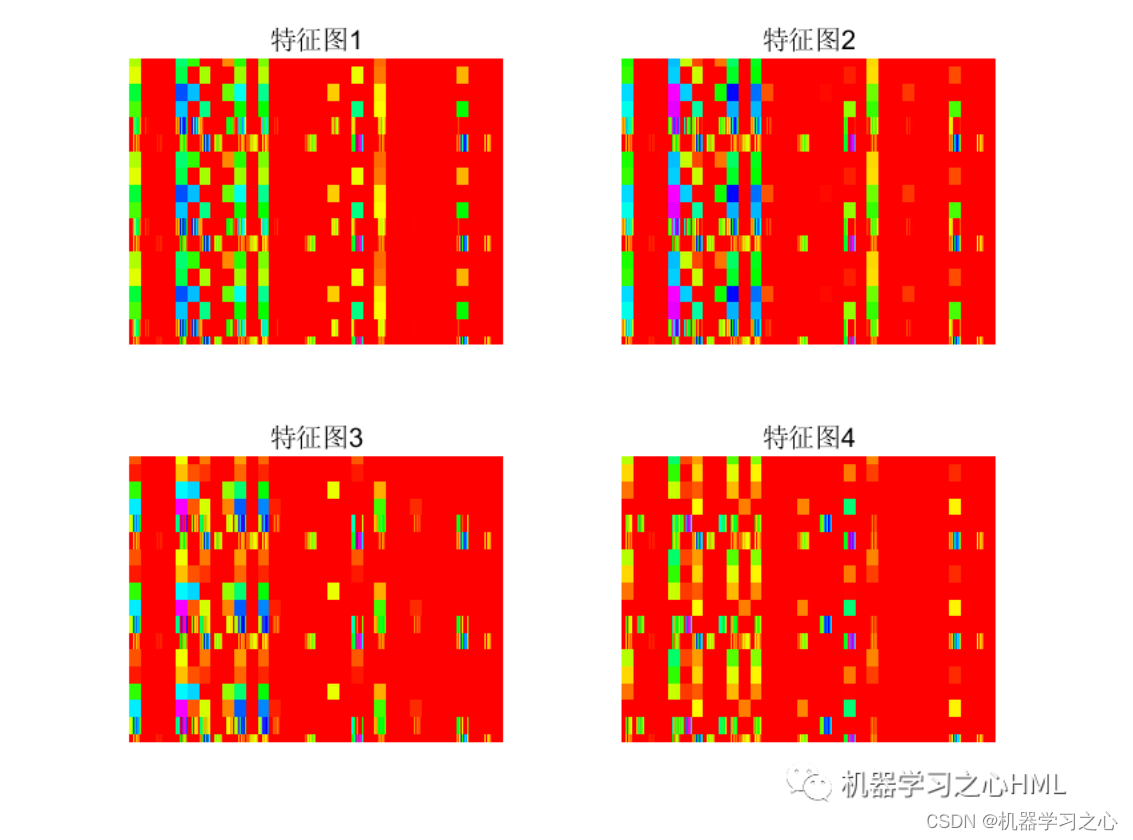
2.运行环境为Matlab2023a及以上,提供损失、RMSE迭代变化极坐标图;网络的特征可视化图;测试对比图;适应度曲线(若首轮精度最高,则适应度曲线为水平直线);
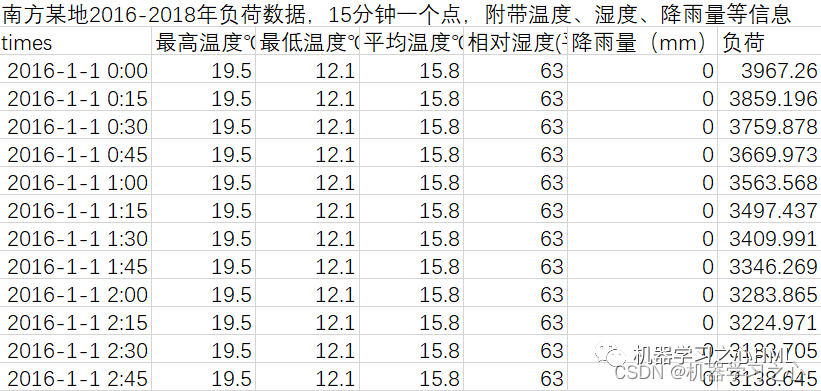
3.excel数据集(负荷数据集),输入多个特征,输出单个变量,考虑历史特征的影响,多变量多步时间序列预测(多步预测即预测下一天96个时间点),main.m为主程序,运行即可,所有文件放在一个文件夹;
4.命令窗口输出SSE、RMSE、MSE、MAE、MAPE、R2、r多指标评价,适用领域:负荷预测、风速预测、光伏功率预测、发电功率预测、碳价预测等多种应用。
程序设计
- 完整源码和数据获取方式:私信博主回复Matlab实现KOA-CNN-BiLSTM-Mutilhead-Attention开普勒算法优化卷积双向长短期记忆神经网络融合多头注意力机制多变量多步时间序列预测。
%% 清除内存、清除屏幕
clc
clear
%% 导入数据
data = xlsread('负荷数据.xlsx');
rng(0)
%% 数据分析
daynum=30; %% 数据量较大,选取daynum天的数据
step=96; %% 多步预测
data =data(end-step*daynum+1:end,:);
%% 特征输入:输入影响因素特征和历史负荷数据
fnum=size(Features,1); %% 变量维度
W_data = data(:,end)'; %% 实际值输出:每天24小时,每小时4个采样点
%% 数据归一化
[features, ~] = mapminmax(Features, 0, 1);
[w_data, ps_output] = mapminmax(W_data, 0, 1);
%% 数据平铺为4-D
LP_Features = double(reshape(features,fnum,step,1,daynum)); %% 特征数据格式
LP_WindData = double(reshape(w_data,step,1,1,daynum)); %% 实际数据格式
%% 格式转换为cell
NumDays = daynum; %% 数据总天数为daynum天
% Kepler优化算法(KOA)
function [Sun_Score, Best_Pos, KOA_curve, bestPred,bestNet,bestInfo ] = KOA(SearchAgents_no, Tmax, ub, lb, dim)
%% 定义
Sun_Pos = zeros(1, dim); %% 包含迄今为止的最优解的向量,表示太阳
Sun_Score = inf; %% 包含迄今为止的最优分数的标量
%% 控制参数
%%
Tc = 3;
M0 = 0.1;
lambda = 15;
%% 第1步:初始化过程
% 轨道离心率 (e)
orbital = rand(1, SearchAgents_no); %% Eq.(4)
%% 轨道周期 (T)
T = abs(randn(1, SearchAgents_no)); %% Eq.(5)
Positions = initialization(SearchAgents_no, dim, ub, lb);%% 初始化行星位置
t = 0; %% 函数评估计数器
%%
%%---------------------评估-----------------------%%
for i = 1:SearchAgents_no
%% 目标函数嵌套
[PL_Fit(i),tsmvalue{i},tnet{i},tinfo{i}] = objectiveFunction(Positions(i,:)');
% 更新迄今为止的最优解
if PL_Fit(i) < Sun_Score %% 问题为最大化时,请将其更改为>
Sun_Score = PL_Fit(i); %% 更新迄今为止的最优分数
Sun_Pos = Positions(i,:); %% 更新迄今为止的最优解
bestPred = tsmvalue{i} ; %% 更新迄今为止的最准确预测结果
bestNet = tnet{i};
bestInfo = tinfo{i};
end
end
while t < Tmax %% 终止条件
[Order] = sort(PL_Fit); %% 对当前种群中的解的适应度值进行排序
%% 函数评估t时的最差适应度值
worstFitness = Order(SearchAgents_no); %% Eq.(11)
M = M0 * (exp(-lambda * (t / Tmax))); %% Eq.(12)
%% 计算表示太阳与第i个解之间的欧几里得距离R
for i = 1:SearchAgents_no
R(i) = 0;
for j = 1:dim
R(i) = R(i) + (Sun_Pos(j) - Positions(i, j))^2; %% Eq.(7)
end
R(i) = sqrt(R(i));
end
%% 太阳和对象i在时间t的质量计算如下:
参考资料
[1] https://blog.csdn.net/kjm13182345320/article/details/128577926?spm=1001.2014.3001.5501
[2] https://blog.csdn.net/kjm13182345320/article/details/128573597?spm=1001.2014.3001.5501