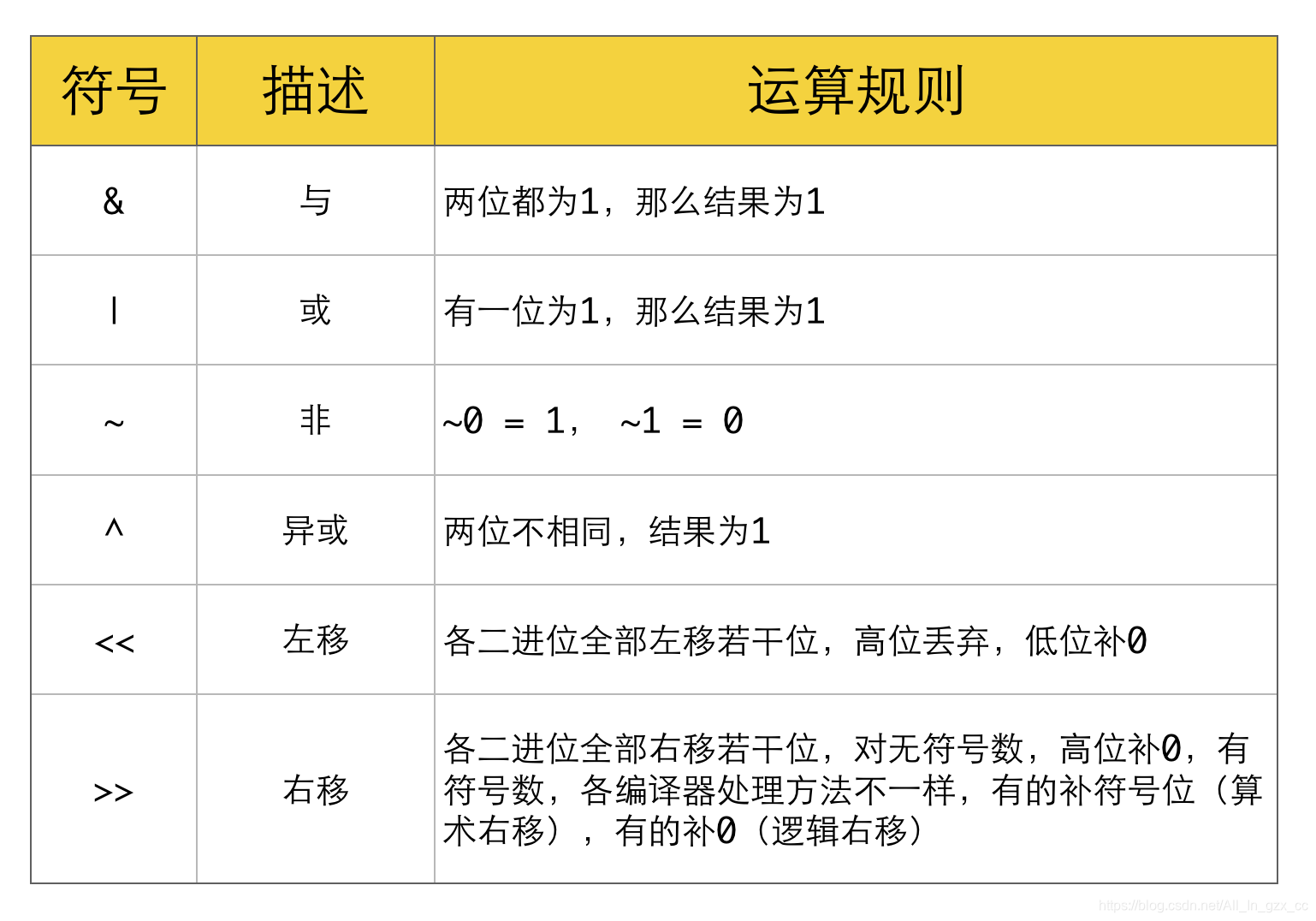
理论
位运算相关基础知识详见此篇 博客
例题
leetcode765. 情侣牵手
N 对情侣坐在连续排列的 2N 个座位上,想要牵到对方的手。 计算最少交换座位的次数,以便每对情侣可以并肩坐在一起。 一次交换可选择任意两人,让他们站起来交换座位。
人和座位用 0 到 2N-1 的整数表示,情侣们按顺序编号,第一对是 (0, 1),第二对是 (2, 3),以此类推,最后一对是 (2N-2, 2N-1)。
这些情侣的初始座位 row[i] 是由最初始坐在第 i 个座位上的人决定的。
思路
这题使用贪心是最简单的方法。该策略是说,我们遍历每个偶数位置 2 * i,把它的对象安排到它右边的奇数位置 2 * i +1。
求数字 xx 的对象时用到了一个技巧,xx 的对象是x ^ 1。解释如下:当 x 是偶数,则其二进制的末尾是 0,所以 x ^ 1 将其二进制的末尾改成 1,于是得到了x的对象 x + 1。 当 x 是奇数,则其二进制的末尾是 1,所以 x ^ 1 将其二进制的末尾改成 0,于是得到了x的对象 x - 1。
class Solution {
public:
//贪心算法:依次遍历数组,将岔开的每对情侣交换到一起,交换一次就+1
int minSwapsCouples(vector<int>& row) {
int n = row.size();
int ans = 0;
//每对判断左右两个是否成对
for(int i = 0; i < n; i += 2){
if(row[i] == (row[i+1] ^ 1)){//使用x异或1可改变二进制数末尾,快速找到x-1或x+1
continue;
}
//不成对就找应该成对的那个交换位置
for(int j = i+2; j < n; j++){
if(row[i] == (row[j] ^ 1)){//若i和j成对,则交换i+1和j
row[i + 1] ^= row[j];
row[j] ^= row[i + 1];
row[i + 1] ^= row[j];//使用异或实现两个数快速交换
}
}
ans += 1;
}
return ans;
}
};
该题还有 并查集解法,详见该篇解答~
leetcode1178. 猜字谜
外国友人仿照中国字谜设计了一个英文版猜字谜小游戏,请你来猜猜看吧。
字谜的迷面 puzzle 按字符串形式给出,如果一个单词 word 符合下面两个条件,那么它就可以算作谜底:
单词 word 中包含谜面 puzzle 的第一个字母。 单词 word 中的每一个字母都可以在谜面 puzzle 中找到。
例如,如果字谜的谜面是 “abcdefg”,那么可以作为谜底的单词有 “faced”, “cabbage”, 和 “baggage”;
而"beefed"(不含字母 “a”)以及 “based”(其中的 “s” 没有出现在谜面中)。
返回一个答案数组answer,数组中的每个元素 answer[i] 是在给出的单词列表 words 中可以作为字谜迷面 puzzles[i]所对应的谜底的单词数目。
思路
这道题只会出现小写字母,种类不多最多26种,而且单词的字符只要在puzzle里出现了就行。即对每个字符来说,就两种状态:是否出现过,可以用0/1 来代表这种相对的状态。
出现过的记为1,没出现过的为0,比如 abc:111,aacc:101,zab:1000…0011(26位)
遍历单词数组,找出单词对应的二进制数,存入map,并统计对应的次数,因为有些单词对应同一个二进制数,比如 abc 和 aaabbc 都是111。
puzzle 的首字符必须要存在于单词中,我们找出所有包含puzzle首字母的puzzle字母组合。
比如aboveyz,满足的组合:a,ab,ao,av,ae,ay,az,abo,abv,abe……都对应有二进制数。而每个单词都对应一个二进制数,如果在其中,则这个单词就是 puzzle 的谜底。
所以,对于 puzzle 的这些二进制数,即它的组合,我们去查看 map 中是否有对应的值 c,如果有,意味着有 c个单词是这样的字母组合,是这个puzzle的谜底。
把当前 puzzle 所有的组合在map中对应的值累加起来,就是当前 puzzle 的谜底单词个数。
其中找所有子集 核心代码 sub = (sub - 1) & puzzleBit; 可参考下面一段话,自己动手算一下即可理解~
假设有字符串abc,对应二进制111,即7。对应所有子集a,b,c,ab,ac,bc,abc,二进制是001,010,100,011,101,110,111;十进制数就是1-7。故此类二进制表示的对象,找子集就找比自身小的数即可,(该处举例三位全是1,所以所有>0且<=7的都是他子集)勿忘&原始值,滤除不对的位置。
class Solution {
public:
vector<int> findNumOfValidWords(vector<string>& words, vector<string>& puzzles) {
map<int, int> w_hash;//key存储每个单词(二进制表示),value为出现次数
vector<int> res(puzzles.size(), 0);
//保存每个word的二进制形式
for(string& word : words){
int bit = getBit(word);
w_hash[bit]++;
}
//遍历puzzles中每个谜面的所有子集情况,若w_hash中出现,当前次数+1
for(int i = 0; i < puzzles.size(); i++){
int puzzleBit = getBit(puzzles[i]);// 当前谜语的二进制数表示
int first = 1 << (puzzles[i][0] - 'a');// 谜语的第一个字符对应的二进制数,比如c就是100
int sub = puzzleBit;//sub为所有可能的组合形式,初始化为puzzleBit
while(sub > 0){//
if((sub & first) != 0 && w_hash[sub] > 0){//包含谜面首字母且该单词在words中存在
res[i] += w_hash[sub];
}
//puzzle的子集对应数字都是比初始puzzle数值小的数,且按位都是1才为1,否则为0。
//n-1是找下一个可能的子集, &puzzle是过滤掉掉不对的位置
sub = (sub - 1) & puzzleBit;
}
}
return res;
}
//获取当前单词的二进制数表示
int getBit(string& word){
int res = 0;
for(int i = 0; i < word.size(); i++){
int offset = word[i] - 'a';// a在最低位,求出当前字符的偏移量
int status = 1 << offset;// 将二进制的1左移offset位,右边用0填充
res = res | status;// 按位或,该位至少有一个1时,才为1(出现过),否则为0
}
return res;
}
};
leetcode338. 比特位计数
给定一个非负整数 num。对于 0 ≤ i ≤ num 范围中的每个数字 i ,计算其二进制数中的 1 的数目并将它们作为数组返回。
思路分析
法1.直接计算
为了表述简洁,下文用「一比特数」表示二进制表示中的 1 的数目。
每个 int 型的数都可以用 32 位二进制数表示,只要遍历其二进制表示的每一位即可得到 1 的数目。
利用位运算的技巧,可以在一定程度上提升计算速度。按位与运算(&)的一个性质是:对于任意整数 x,
令 x=x&(x−1),该运算将 x 的二进制表示的最后一个 1 变成 0。因此,对 x 重复该操作,直到 x 变成 0,则操作次数即为 x 的「一比特数」。
另外,部分编程语言有相应的内置函数,例如 Java 的 \Integer.bitCount,C++ 的 __builtin_popcount,Go 的 bits.OnesCount 等,读者可以自行尝试。
class Solution {
public:
int countOnes(int x) {
int ones = 0;
while (x > 0) {
x &= (x - 1);
ones++;
}
return ones;
}
vector<int> countBits(int num) {
vector<int> bits(num + 1);
for (int i = 0; i <= num; i++) {
bits[i] = countOnes(i);
}
return bits;
}
};
法2.动态规划
事实上,这道题是有严格 O(n) 的解法的,要求 O(n) 复杂度又是输出方案的题,通常就是递推的 DP 题。
用 已算出的值 去凑出 要算的值。
那么对于这类问题我们该如何考虑呢?一般是靠经验,如果实在没见过这类题型的话,我们就需要在纸上画一下,分析一下我们朴素做法的最后一步是怎么进行的。
不失一般性的,假设当前我要统计的数的 i,i 对应的二进制表示是 00000…0010100101(共 32 位)
如果我们是使用「朴素解法」求解的话,无论是从高位进行统计,还是从低位进行统计,最后一位扫描的都是边缘的数(如果是 1 就计数,不是 1 就不计数)。
- 从低位到高位,最后一步在扫描最高位之前,统计出 1 的个数应该等同于将 i 左移一位,并在最低位补 0,也就是等于 ans[i <<1],这时候就要求我们在计算 i 的时候 i << 1 已经被算出来(从大到小遍历)
- 从高位到低位,最后一步在扫描最低位之前,统计出 1 的个数应该等同于将 i 右移一位,并在最高位补 0,也就是等于 ans[i >>1],这时候就要求我们在计算 i 的时候 i >> 1 已经被算出来(从小到大遍历)
通过最后一步分析,转移方程就出来了:
- 当从大到小遍历 :f(i) =f(i <<1) +((i >>31)& 1)
- 当从小到大遍历 :f(i)=f(i>>1)+(i&1)
推导过程可参考法3的解析~
//从小到大遍历
class Solution {
public:
//根据奇偶性手动枚举可看出规律,该规律即为DP状态转移方程
vector<int> countBits(int num) {
vector<int> ans(num+1);
// ans[i] = 「i >> 1 所包含的 1 的个数」+「i 的最低位是否为 1」
for(int i = 1; i <= num; i++){
ans[i] = ans[i >> 1] + (i & 1);
}
return ans;
}
};
class Solution {
// 从大到小遍历
public int[] countBits(int n) {
int[] ans = new int[n + 1];
for (int i = n; i >= 0; i--) {
// 如果计算 i 所需要的 i << 1 超过 n,则不存储在 ans 内,需要额外计算
int u = i << 1 <= n ? ans[i << 1] : getCnt(i << 1);
// ans[i] =「i << 1 所包含的 1 的个数」 + 「i 的最高位是否为 1」
ans[i] = u + ((i >> 31) & 1);
}
return ans;
}
int getCnt(int u) {
int ans = 0;
for (int i = 0; i < 32; i++) ans += (u >> i) & 1;
return ans;
}
};
常用位运算公式
- a >> b & 1 代表检查 a 的第 b 位是否为 1,有两种可能性 0 或者 1
- a += 1 << b 代表将 a 的第 b 位设置为 1 (当第 b 位为 0 的时候适用)
如不想写对第 b 位为 0 的前置判断,a += 1 << b 也可以改成 a |= 1 << b
PS. 1 的二进制就是最低位为 1,其他位为 0 哦;>>运算符 优先级 高于 &运算符哦
以上两个操作在位运算中使用频率超高,建议都加深理解。
法3.根据奇偶性
对于所有的数字,只有两类:
奇数:二进制表示中,奇数一定比前面那个偶数多一个 1,因为多的就是最低位的 1。
举例: 0 = 0 1 = 1 2 = 10 3 = 11偶数:二进制表示中,偶数中 1 的个数一定和除以 2 之后的那个数一样多。因为最低位是 0,除以 2 就是右移一位,也就是把那个 0 抹掉而已,所以 1 的个数是不变的。
举例: 2 = 10 4 = 100 8 = 1000 3 = 11 6 = 110 12 = 1100另外,0 的 1 个数为 0,于是就可以根据奇偶性开始遍历计算了。
vector<int> countBits(int num) {
vector<int> result(num+1);
result[0] = 0;
for(int i = 1; i <= num; i++)
{
if(i % 2 == 1)
{
result[i] = result[i-1] + 1;
}
else
{
result[i] = result[i/2];
}
}
return result;
}
leetcode191. 位1的个数
编写一个函数,输入是一个无符号整数(以二进制串的形式),返回其二进制表达式中数字位数为 ‘1’ 的个数(也被称为汉明重量)。
关于uint32_t 的 介绍
思路分析
观察这个运算:n & (n−1),其预算结果恰为把 n 的二进制位中的最低位的 1 变为 0 之后的结果。
如:6 = (110), 4 = (100) ,6 & (6−1)=4,运算结果 4 即为把 6 的二进制位中的最低位的 1 变为 0 之后的结果。
这样我们可以利用这个位运算的性质加速我们的检查过程,在实际代码中:我们不断让当前的 n 与 n - 1 做与运算,直到 n 变为 0 即可。 因为每次运算会使得 n 的最低位的 1 被翻转,因此运算次数就等于 n 的二进制位中 1 的个数。
class Solution {
public:
int hammingWeight(uint32_t n) {
int cnt = 0;
while(n){
n &= (n - 1);
cnt++;
}
return cnt;
}
};
多种解答方法详见 解答
类似题目:
- 颠倒二进制位
- 2的幂
- 比特位计数