目录
一.dfs简介
深度优先搜索,简称dfs。它在百度上的解释是这样的:
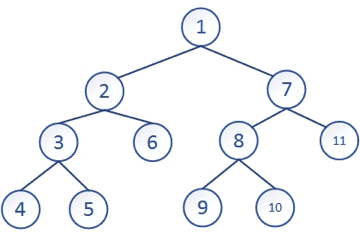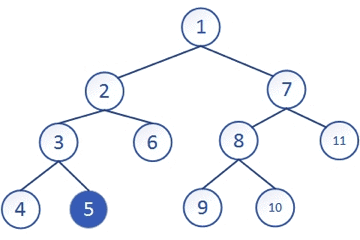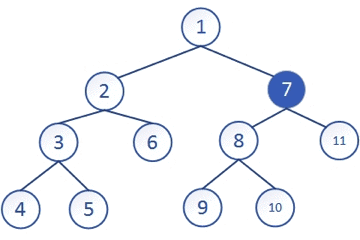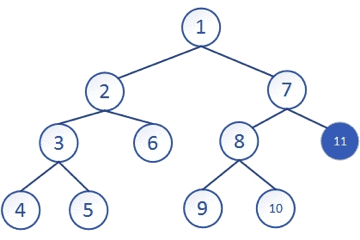
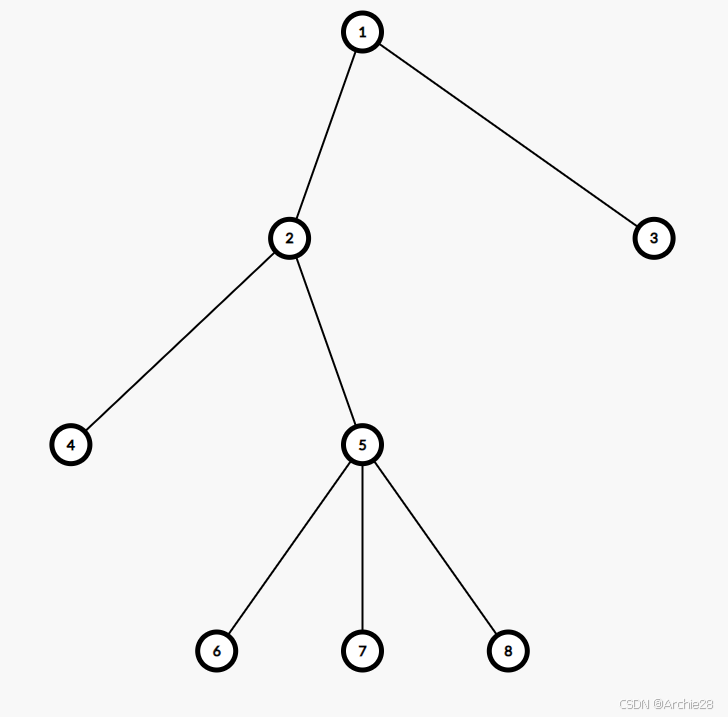
但这跟C++中的dfs关系并不大。在C++中dfs是指对于某一个节点,进行拓展时可能有若干种方式,以深度为第一优先级进行遍历的方式。就像在下图中,我们先将一个节点走到最深处,如果没有路,就返回上一个节点看有没有其他路径,它的搜索路径就是:1-2-3-4-5-6-7-8-9-10-11。
我们通常使用递归来进行搜索,以下为dfs的搜索模板:
#include<bits/stdc++.h>
using namespace std;
char a[10][10];
bool vis[10][10];
int n,m,dx[5]={0,-1,1,0,0},dy[5]={0,0,0,-1,1},ans=INT_MAX;
void dfs(int x,int y,int step){
if(){//递归出口
//结束后要做的
}
int nx,ny;
for(int i=1;i<=4;i++){
nx=x+dx[i],ny=y+dy[i];//坐标移动
if(nx<1||nx>n||ny<1||ny>m) continue;
if(a[nx][ny]=='#'||vis[nx][ny]==1) continue;
vis[nx][ny]=1;
dfs(nx,ny,step+1);
vis[nx][ny]=0;
}//vis标记以走过的路
}
int main() {
cin>>n>>m;
for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) cin>>a[i][j];
dfs(1,1,1);
//输出需要输出的数
return 0;
}二.dfs的运用
1.迷宫问题
在进行搜索枚举时,我们知道从初始状态(起点)到最终状态(终点),每一步都做了一次选择,我们可以思考一下,如何将每一步的选择都进行记录,这也就是我们记录搜索的路径。
要记录路径我们可以:
1.记录每一个节点的深度即dfs中增加一个状态。
2.用数组记录每一个深度下的选择。
此时,当某一条路径从s进行dfs搜索到t时,我们就记录了每一步的选择,最后到达终点时,我们便可以进行路径的输出。
经典题型:最快走出迷宫
一个迷宫由R行C列格子组成,有的格子里有障碍物,不能走;
有的格子是空地,可以走。 给定一个迷宫,求从左上角走到右下角最少需要走多少步(数据保证一定能走到)。
只能在水平方向或垂直方向走,不能斜着走。
数据范围:
1≤ R,C ≤ 10
题目分析:
这就是一道最简单的dfs模板题,我们仅需将所有路径递归出来,再用打擂台的方法求出最小值即可。正确代码如下:
#include<bits/stdc++.h>
using namespace std;
char a[10][10];
bool vis[10][10];
int n,m,dx[5]={0,-1,1,0,0},dy[5]={0,0,0,-1,1},ans=INT_MAX;
void dfs(int x,int y,int step){
if(x==n&&y==m){
ans=min(ans,step);
return;
}
int nx,ny;
for(int i=1;i<=4;i++){
nx=x+dx[i],ny=y+dy[i];
if(nx<1||nx>n||ny<1||ny>m) continue;
if(a[nx][ny]=='#'||vis[nx][ny]==1) continue;
vis[nx][ny]=1;
dfs(nx,ny,step+1);
vis[nx][ny]=0;
}
}
int main() {
cin>>n>>m;
for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) cin>>a[i][j];
dfs(1,1,1);
cout<<ans;
return 0;
}2.棋盘问题:
经典题型:八皇后问题
题目描述:
在国际象棋棋盘上放置八个皇后,要求每两个皇后之间不能直接吃掉对方。按给定顺序和格式输出所有八皇后问题的解(见样例)。
题目分析:
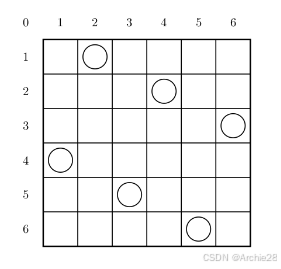
首先,皇后的走法与其他的棋子不同,她可以横向、纵向和斜向移动,所以要标记就需要她所在的那一行、一列,两斜线。
第二,要注意的是他要输出的是所有情况。
(此图片只是演示,并不是这到题的真正可能)
正确代码:
#include<bits/stdc++.h>
using namespace std;
int a[50][50];
bool x[50],r[50],l[50];
int k;
void dfs(int y){
if(y==9){
k++;
cout<<"No. "<<k<<endl;
for(int i=1;i<=8;i++){
for(int j=1;j<=8;j++){
cout<<a[i][j]<<' ';
}
cout<<endl;
}
return ;
}//出口,将坐标转换为图形
for(int i=1;i<=8;i++){
if(x[i]||l[i+y]||r[i-y+8]) continue;
x[i]=l[i+y]=r[i-y+8]=1;
a[i][y]=1;
dfs(y+1);
x[i]=l[i+y]=r[i-y+8]=0;
a[i][y]=0;
}//记录坐标
}
int main() {
dfs(1);
return 0;
}3.排列与组合:
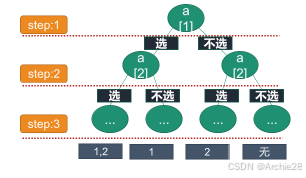
排列组合类型的题目就是选与不选的抉择。我们关注的是选了哪些数字(内容)
对于每个数选和不选的两种情况进行两次dfs拓展。组合能枚举到所有情况,但是不关注选择的先后顺序,我们知道选了哪些数,但是顺序是不清晰的。整体复杂度为O(2n)。我们可以使用回溯进行试探性选择,这样就可以枚举出所有不同的选择顺序。
经典类题:数字全排列
题目描述:
在一个集合{ 1,2,3...,n }中,请输出这些数字的所有排列方式.。
数据范围:
n<=10
题目分析:
n个数的全排列,可以理解成做n次选择,每次在[1,n]中选择一个数(选过的不再选)。
这样很容易画出一个树形结构。当所有的数都已经被选完后,则输出当前的选择序列。
正确代码:
#include<bits/stdc++.h>
using namespace std;
int n,shu[15];
bool vis[11];
void dfs(int x){
if(x==n+1){
for(int i=1;i<=n;i++){
cout<<shu[i]<<" ";
}
cout<<endl;
return;
}
for(int i=1;i<=n;i++){
if(vis[i]==true) continue;
vis[i]=true;
shu[x]=i;
dfs(x+1);
vis[i]=false;
}
}
int main(){
cin>>n;
dfs(1);
return 0;
}三.总结
dfs的优点主要包括实现简单、易于理解,并且适用于解决许多问题。
Ⅰ.实现简单、易于理解:dfs算法的实现逻辑相对直观和简单,使得它易于被编程人员理解和实现。这种算法适合那些需要递归探索所有可能路径的问题,如图的遍历、树的搜索等。
Ⅱ.适用性问题广泛:dfs算法在计算机科学领域有着广泛的应用,能够解决包括但不限于图的遍历、全排列生成、最短路径搜索等问题。这些问题的共同特点是需要探索所有可能的状态或路径,以找到解决方案或确定是否存在解决方案。
尽管dfs算法具有上述优点,但它也存在一些潜在的缺点,例如可能会陷入无限循环(对于非连通图)或不一定能找到最短路径等。因此,在实际应用中,选择使用DFS算法还是需要根据具体问题的特性和需求来决定。