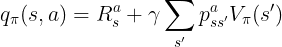1.在解释马尔可夫决策问题之前,我们首先应该知道马尔可夫过程(Markov Process),简单理解就是未来的行为只取决于现在的状态,而与之前的状态无关。设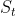
![p[S_{t+1}|S_t]=p[S_{t+1}|S_1,S_2,...,S_t]](/image/aHR0cHM6Ly9pLWJsb2cuY3NkbmltZy5jbi9ibG9nX21pZ3JhdGUvYjJjNTUzYjYzZTBhNTE2NzkyYzYzZTBlOTMzNGNlZjEuZ2lm)
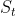
我们讨论一个简单问题时,状态的数目是有限的,不妨设为n个。从而给出状态转移矩阵的定义:
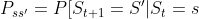
2.基于马尔可夫过程,我们引入奖励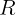
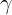
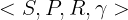
![\large R_s=E[R_{t+1}|S_t=s]](/image/aHR0cHM6Ly9pLWJsb2cuY3NkbmltZy5jbi9ibG9nX21pZ3JhdGUvNThjZmM5ZjQxNjMxODNkM2M0N2YyNDkxZThkYTQ3MjEuZ2lm_s%3DE%5BR_%7Bt+1%7D%7CS_t%3Ds%5D)
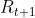
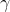
3.在此之前,我们都没有考虑在某一个状态时如何采取行动,显而易见,在特定的一个状态,可以采取的动作是多样的且有限的,因此我们引入一个新的元素,活动集A,从而引出马尔科夫决策问题tuple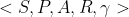
此时,我们有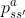
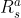
我们给定某一个策略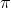

![\large {\color{Red} V_\pi(s)=E_\pi[\sum_{k=0}^{\infty }\gamma^k R_{t+k+1}|S_t=s]}](/image/aHR0cHM6Ly9pLWJsb2cuY3NkbmltZy5jbi9ibG9nX21pZ3JhdGUvZmYxYjdkZDIzYzFmYmYwYTNiZDBiYzk0NzY1ZjkxNjIuZ2lm)
动作值函数:
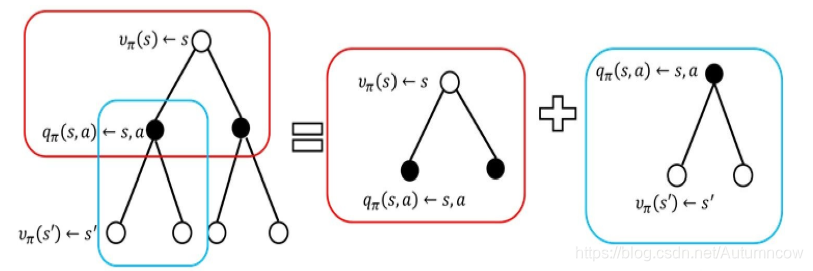
基于上面的两个式子,我们给出贝尔曼方程:
同样的,我们可以得到
在这个图中,我们简单的往前看两步,可以看到,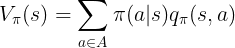
将后者带入前式可以得到
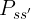
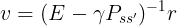
通过以上的方法,我们可以计算出每个状态的值函数,我们的任务是在问题中找到某一条路径,使得最后收获的值函数收获最大
参考文献:
《深入浅出强化学习-原理入门》,郭宪,方勇纯编著,电子工业出版社,2018.1

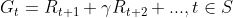
![\large {\color{Red} q_\pi(s,a)=E_\pi[\sum_{k=0}^{\infty }\gamma^k R_{t+k+1}|S_t=s,A_t=a]}](/image/aHR0cHM6Ly9pLWJsb2cuY3NkbmltZy5jbi9ibG9nX21pZ3JhdGUvY2FhMWMxOTU2NzY5YzA4YTNlOTRiOGNmNGNiNWQzOTcuZ2lm)
![\large V(s)=E[G_t|S_t=s]=E[R_{t+1}+\gamma R_{t+2}+...|S_t=s]](/image/aHR0cHM6Ly9pLWJsb2cuY3NkbmltZy5jbi9ibG9nX21pZ3JhdGUvY2VhYTczNjNiMjQ3ZTViMjcwMDYyODU2YTJhMmY4ZDkuZ2lm)
![\large =E[R_{t+1}+\gamma G_{t+1}|S_t=s]=E[R_{t+1}+\gamma V(S_{t+1})|S_t=s]](/image/aHR0cHM6Ly9pLWJsb2cuY3NkbmltZy5jbi9ibG9nX21pZ3JhdGUvMzllMDFhZjUxMWI3MTIxNjM5ZmEyZDZiNGRmNTI1MmYuZ2lm)
![\large q_\pi(s,a)=E[R_{t+1}+\gamma q_\pi(S_{t+1},A_{t+1})|S_t=s,A_t=a]](/image/aHR0cHM6Ly9pLWJsb2cuY3NkbmltZy5jbi9ibG9nX21pZ3JhdGUvOTNjM2Q1M2U2NmVhODJiMmI0ZWEyOGE5NzhjODVlOTIuZ2lm)