目录
课前先导
每60秒记作一分钟,每60分钟记作一小时,我们的时间是逢六十进一;
每24小时记作一天,天数是逢24进1;
什么是进制?
进制也就是进位计数制,是人为定义的带进位的计数方法。我们的时间就是六十进制,天数是二十四进制;对于任何一种进制---X进制,就表示每一位上的数运算时都是逢X进一位。
计算机中主要有十进制、二进制、八进制、十六进制:
十进制:0 1 2 3 4 5 6 7 8 9 逢十进一
二进制:0 1 逢二进一
八进制:0 1 2 3 4 5 6 7 逢八进一
十六进制:0 1 2 3 4 5 6 7 8 9 A(10) B(11) C(12) D(13) E(14) F(15) 逢十六进一
今天我们就来学习一下计算机中的进制,以及它们之间的互相转换。
一、计算机中的进制数
十进制(简写:D)
十进制的基数为10,数码由0-9组成,计数规律逢十进一。我们平常说的数字,就是十进制。
十进制:0 1 2 3 4 5 6 7 8 9 逢十进一
二进制(简写:B)
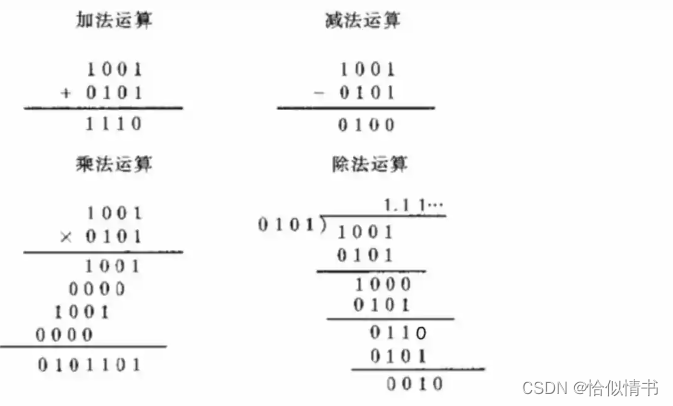
二进制有两个特点:它由两个数码0,1组成;二进制数运算规律是逢二进一。
二进制:0 1 逢二进一
加运算:0+0=0,0+1=1,1+0=1,1+1=10,(逢2进1);
减运算:1-1=0,1-0=1,0-0=0,0-1=1,(向高位借1当2);
乘运算:0×0=0,0×1=0,1×0=0,1×1=1,(只有同时为“1”时结果才为“1”);
除运算:0÷1=0,1÷1=1 (二进制数只有两个数(0,1),因此它的商是1或0)
计算机内部使用二进制形式表示数据
八进制(简写:Q)
八进制的基数为8,数码由0-7组成,计数规律逢八进一。
八进制:0 1 2 3 4 5 6 7 逢八进一
十六进制(简写:H)
十六进制数有两个基本特点:它由十六个数码:数字0~9加上字母A-F组成(它们分别表示10~15),十六进制数运算规律是逢十六进一。
二、计算机进制数之间的转换
1、十进制转二进制
一个十进制数转换为二进制数要分整数部分和小数部分分别转换,最后再组合到一起。
整数:
采用 "除2取余,逆序排列"法。具体做法是:用2整除十进制整数,可以得到一个商和余数;再用2去除商,又会得到一个商和余数,如此进行,直到商为小于1时为止,然后把先得到的余数作为二进制数的低位有效位,后得到的余数作为二进制数的高位有效位,依次排列起来
789=1100010101(B)......................B表示二进制
789/2=394 余1 第10位
394/2=197 余0 第9位
197/2=98 余1 第8位
98/2=49 余0 第7位
49/2=24 余1 第6位
24/2=12 余0 第5位
12/2=6 余0 第4位
6/2=3 余0 第3位
3/2=1 余1 第2位
1/2=0 余1 第1位
小数:
十进制小数转换成二进制小数采用"乘2取整,顺序排列"法。具体做法是:用2乘十进制小数,可以得到积,将积的整数部分取出,再用2乘余下的小数部分,又得到一个积,再将积的整数部分取出,如此进行,直到积中的小数部分为零,此时0或1为二进制的最后一位。或者达到所要求的精度为止。
然后把取出的整数部分按顺序排列起来,先取的整数作为二进制小数的高位有效位,后取的整数作为低位有效位。
0.7=(0.1 0110 0110...)B
0.7*2=1.4========取出整数部分1
0.4*2=0.8========取出整数部分0
0.8*2=1.6========取出整数部分1
0.6*2=1.2========取出整数部分1
0.2*2=0.4========取出整数部分0
0.4*2=0.8========取出整数部分0
0.8*2=1.6========取出整数部分1
0.6*2=1.2========取出整数部分1
0.2*2=0.4========取出整数部分0
2、十进制转八进制
十进制转八进制的方法有两种:
间接法:讲十进制数转化成二进制数,然后再转八进制数。
我们这里讲一下直接法:
整数:
采用 "除8取余,逆序排列"法。具体做法是:用8整除十进制整数,可以得到一个商和余数;再用8去除商,又会得到一个商和余数,如此进行,直到商为小于1时为止,然后把先得到的余数作为八进制数的低位有效位,后得到的余数作为八进制数的高位有效位,依次排列起来
150=226(Q).....................Q表示八进制
150/8=18 余6第3位
18/8=2 余2 第2位
2/8=0 余2 第1位
小数:
十进制小数转换成八进制小数采用"乘8取整,顺序排列"法。具体做法是:用8乘十进制小数,可以得到积,将积的整数部分取出,再用8乘余下的小数部分,又得到一个积,再将积的整数部分取出,如此进行,直到积中的小数部分为零,或者达到所要求的精度为止。
然后把取出的整数部分按顺序排列起来,先取的整数作为八进制小数的高位有效位,后取的整数作为低位有效位。
0.12 = 0753412172702436(Q)
0.12 * 8 = 0.96========取出整数部分0
0.96 * 8 = 7.68========取出整数部分7
0.68 * 8 = 5.44========取出整数部分5
0.44 * 8 = 3.52========取出整数部分3
0.52 * 8 = 4.16========取出整数部分4
..............................................
150.12 = 226.075(Q)(保留三位小数)
3、十进制转十六进制
十进制转十六进制的方法有两种:
间接法:将十进制数转化成二进制数,然后再转十六进制数。
我们这里讲一下直接法:
整数:
采用 "除16取余,逆序排列"法。具体做法是:用16整除十进制整数,可以得到一个商和余数;再用16去除商,又会得到一个商和余数,如此进行,直到商为小于1时为止,然后把先得到的余数作为十六进制数的低位有效位,后得到的余数作为十六进制数的高位有效位,依次排列起来
2526 = 9DE(H).....................H表示十六进制
2526/16 = 157 余14第3位
157/16 = 9 余13第2位
9/16 = 0 余9第1位
小数:
十进制小数转换成十六进制小数采用"乘16取整,顺序排列"法。具体做法是:用16乘十进制小数,可以得到积,将积的整数部分取出,再用16乘余下的小数部分,又得到一个积,再将积的整数部分取出,如此进行,直到积中的小数部分为零,或者达到所要求的精度为止。
然后把取出的整数部分按顺序排列起来,先取的整数作为十六进制小数的高位有效位,后取的整数作为低位有效位。
0.9232 = 0.E7381(H)
0.9232 * 16 = 14.4512 ========取出整数部分14
0.4512 * 16 = 7.2192========取出整数部分7
0.2192 * 16 = 3.5072========取出整数部分3
0.5072 * 16 = 8.1152========取出整数部分8
0.1152 * 16 = 1.8432========取出整数部分1
................................
2526.9232 = 9DE.E73(H)(保留三位小数)
4、二进制转十进制
方法一:按位权展开求和
1001.01(B)
=1*(2^3)+0*(2^2)+0*(2^1)+1*(2^0)+0*(2^-1)+1*(2^-2)
=8+0+0+1+0+0.25
=9.25
方法二:
把二进制数首先写成加权系数展开式,然后按十进制加法规则求和。这种做法称为"按权相加"法。
2的0次方是1(任何数的0次方都是1,0的0次方无意义)
2的1次方是2
2的2次方是4
2的3次方是8
2的4次方是16
2的5次方是32
2的6次方是64
2的7次方是128
2的8次方是256
2的9次方是512
...................
如:100011=32+0+0+0+2+1=35
5、二进制转八进制
整数部分:从右往左每三位一组,缺位处用0填补,然后每组按十进制方法进行转化;
小数部分:从左到右每三位一组,缺位处用0填补,然后每组按十进制方法进行转化。
6、二进制转十六进制
整数部分:从右往左每四位一组,缺位处用0填补,然后每组按十进制方法进行转化;
小数部分:从左到右每四位一组,缺位处用0填补,然后每组按十进制方法进行转化。
7、八进制转二进制
整数部分:从右往左每一位八进制数看做十进制数,转换为三位二进制数,缺位处用0补充;
小数部分:从左往右每一位八进制数看做十进制数,转换为三位二进制数,缺位处用0补充;
8、八进制转十进制
按位权展开求和:
72.45Q
=7*(8^1)+2*(8^0)+4*(8^-1)+5*(8^-2)
=56+2+0.5+0.078125
=58.578125
9、八进制转十六进制
先将八进制数转换为二进制数,然后再将二进制数转换为十六进制数。
10、十六进制转二进制
整数部分:从右往左每一位十六进制数看做十进制数,转换为四位二进制数,缺位处用0补充;
小数部分:从左往右每一位十六进制数看做十进制数,转换为三四位二进制数,缺位处用0补充;
11、十六进制转八进制
先将十六进制数转换为二进制数,再将二进制数转换为八进制数。
12、十六进制转十进制
38A.11H
=3*(16^2)+8*(16^1)+10*(16^0)+1*(16^-1)+1*(16^-2)
=768+128+10+0.0625+0.0039
=906.0664
今天关于计算机进制数的学习到此就算结束了,学习进制转换虽然在我们的编程中用的不多,但大家还是抽点时间了解一下,技多不压身嘛。好了,我是一米八,有腹肌,低于半小时你报警的Loveletter,觉得本篇博文写的不错的小伙伴,麻烦点点关注,我们下篇博文见。




