题目要求

将一系列给定数字插入一个初始为空的最小堆 h。随后对任意给定的下标 i，打印从第 i 个结点到根结点的路径。 

输入格式  

每组测试第 1 行包含 2 个正整数 n 和 m (≤103)，分别是插入元素的个数、以及需要打印的路径条数。下一行给出区间 [−104,104] 内的 n 个要被插入一个初始为空的小顶堆的整数。最后一行给出 m 个下标。 

输出格式 

对输入中给出的每个下标 i，在一行中输出从第 i 个结点到根结点的路径上的数据。数字间以 1 个空格分隔，行末不得有多余空格。 

输入样例 

5 3
46 23 26 24 10
5 4 3 

输出样例 

24 23 10
46 23 10
26 10 

题解  

        思路如注释所示，可通过所有测试点

#include<bits/stdc++.h>
using namespace std;           
typedef struct HeapStruct *MinHeap;
#define ElementType int
#define MinData -10005
struct HeapStruct{
	ElementType *Elements;//元素类型的数组 
	int Size;             //堆的当前元素个数 
	int Capacity;	      //堆的最大容量 
};

MinHeap creat(int MaxSize){
	MinHeap H = (MinHeap)malloc(sizeof(struct HeapStruct));
	H->Elements =(int *)malloc((MaxSize+1)*sizeof(ElementType));
	H->Size = 0;
	H->Capacity = MaxSize;
	H->Elements[0] = MinData;
	return H;
}
 
bool IsFull(MinHeap H){
	return (H->Size==H->Capacity);
}

void Insert(MinHeap H,ElementType item){
	int i;
	if(IsFull(H)){
		cout<<"最小堆已满";
		return; 
	}
	i = ++H->Size;    //先对元素个数加一，在把待插入元素的位序改为队尾 
	for(;H->Elements[i/2]>item&&i>1;i=i/2){
		H->Elements[i] = H->Elements[i/2];   //依次与父节点比较，若父节点较小则把父节拉下来 
	}
	H->Elements[i] = item;   //把合适插入位置上的元素值改为item 
} 

bool IsEmpty(MinHeap H){
	return (H->Size==0);
}

void Print(MinHeap H,int i){
	if(IsEmpty(H)){
		cout<<"堆为空";
		return; 
	}
	else{
		int flag=1;      //用flag记录是否为第一个元素，第一个元素前不加空格
		for(;i>0;i=i/2){   //因为该函数是值传递，所以循环中直接用i就行，便于理解， （根据堆排序的特点父节点的下标为子节点下标的1/2）
			if(flag==1){
				cout<<H->Elements[i];
				flag = 0;
			}
			else cout<<' '<<H->Elements[i];
		}	
	}
} 

int main(){
	int N,T;
	MinHeap H;
	cin>>N>>T;
	H = creat(N);
	
	while(N--){
		int n;
		cin>>n;
		Insert(H,n);
	}	
	while(T--){
		int i;
		cin>>i;
		Print(H,i);
		cout<<'\n';		
	}	
} 

        这道题可以看作是堆的操作集的阉割版，没有对堆中的元素进行删除（对堆的操作中删除操作最为复杂），直接对指定下标的元素寻找路线（也就是父节点） 。该题有以下几个要点。

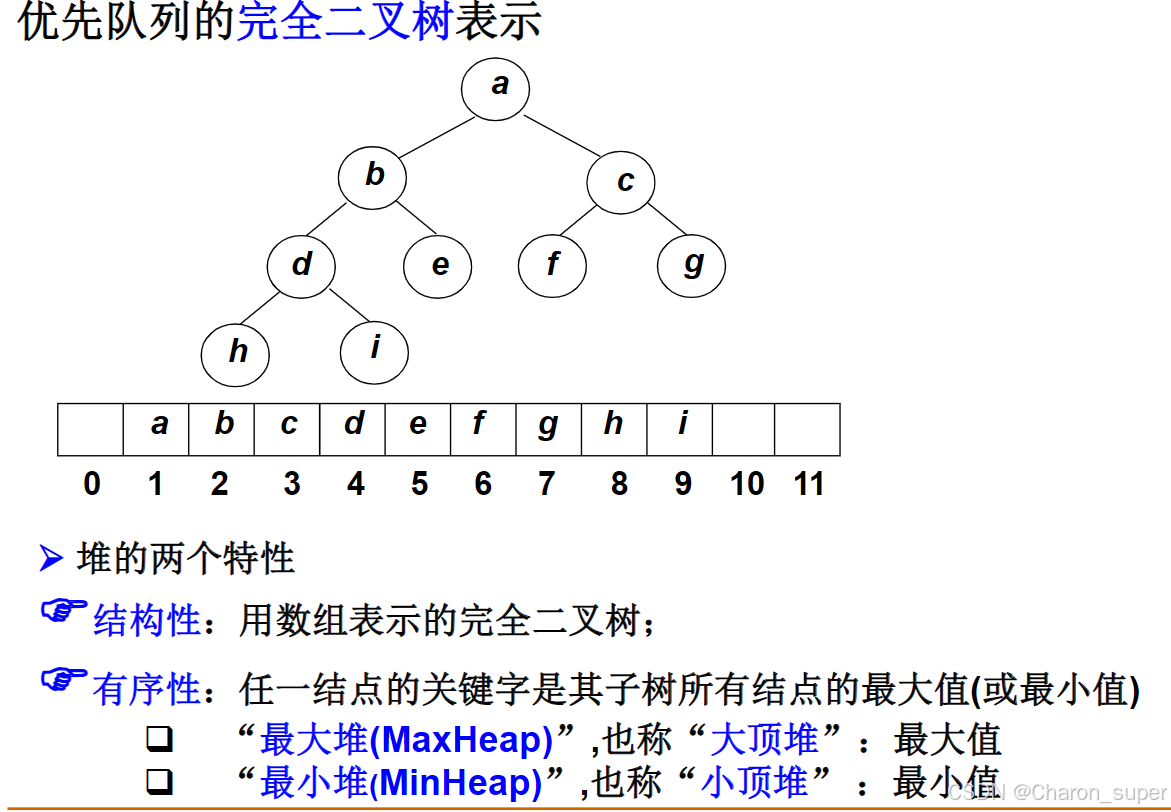
        1.堆的下标特性：堆排序的特点，父节点的下标为子节点下标的1/2（这点很重要，为整个题的基石），左子树下标为父节点下标的2倍，右子树为2倍加1。

        2.每次插入时要注意整个堆的有序性，初始插入位置为叶子节点，然后依次和已排序的父节点进行比较。

         此系列为作者记录数据结构学习文章，由于能力所限，难免有细节处理不当之处，恳请读者谅解并指正。