1. Non-local
Non-Local是王小龙在CVPR2018年提出的一个自注意力模型。Non-Local NN和Non-Local Means非局部均值去燥滤波有点相似的感觉。普通的滤波都是3×3的卷积核,然后在整个图片上进行移动,处理的是3×3局部的信息。Non-Local Means操作则是结合了一个比较大的搜索范围,并进行加权。详见:https://blog.csdn.net/qianhen123/article/details/81043217
在Non-Local NN这篇文章中的Local也与以上有一定关系,主要是针对感受野来说的,一般的卷积的感受野都是3×3或5×5的大小,而使用Non-Local可以让感受野很大,而不是局限于一个局部领域。
与之前介绍的CBAM模块,SE模块,BAM模块,SK模块类似,Non-Local也是一个易于集成的模块,针对一个feature map进行信息的refine, 也是一种比较好的attention机制的实现。不过相比前几种attention模块,Non-Local中的attention拥有更多地理论支撑,稍微有点晦涩难懂。
Non-local的通用公式表示:
y i = 1 C ( x ) ∑ ∀ j f ( x i , x j ) g ( x j ) y_i=\frac{1}{C(x)}\sum_{\forall j}f(x_i,x_j)g(x_j) yi=C(x)1∀j∑f(xi,xj)g(xj)
- x是输入信号,cv中使用的一般是feature map
- i 代表的是输出位置,如空间、时间或者时空的索引,他的响应应该对j进行枚举然后计算得到的
- f 函数式计算i和j的相似度
- g 函数计算feature map在j位置的表示
- 最终的y是通过响应因子C(x) 进行标准化处理以后得到的
理解:与Non local mean相比,就很容易理解,i代表的是当前位置的响应,j代表全局响应,通过加权得到一个非局部的响应值。
Non-Local的优点是什么?
- 提出的non-local operations通过计算任意两个位置之间的交互直接捕捉远程依赖,而不用局限于相邻点,其相当于构造了一个和特征图谱尺寸一样大的卷积核, 从而可以维持更多信息。
- non-local可以作为一个组件,和其它网络结构结合,经过作者实验,证明了其可以应用于图像分类、目标检测、目标分割、姿态识别等视觉任务中,并且效果不错。
- Non-local在视频分类上效果很好,倾向于使用在视频分类这个领域中。
2. 细节
给了通用公式,然后分别介绍f函数和g函数的实例化表示:
g函数:可以看做一个线性转化(Linear Embedding)公式如下:
g
(
x
j
)
=
W
g
x
j
g(x_j)=W_gx_j
g(xj)=Wgxj
W
g
W_g
Wg是需要学习的权重矩阵,可以通过空间上的1×1卷积实现(实现起来比较简单)。
**f函数:**这是一个用于计算i和j相似度的函数,作者提出了四个具体的函数可以用作f函数。
- Gaussian function: 具体公式如下:
f ( x i , x j ) = e x i T x j C ( x ) = ∑ ∀ j f ( x i , x j ) f(x_i,x_j)=e^{x_i^Tx_j} \\ C(x)=\sum_{\forall j}f(x_i,x_j) f(xi,xj)=exiTxjC(x)=∀j∑f(xi,xj)
这里使用的是
x
i
T
x
j
x_i^Tx_j
xiTxj一个点乘来计算相似度,之所以点积可以衡量相似度,这是通过余弦相似度简化而来的。
a
⃗
∗
b
⃗
=
∣
a
⃗
∣
∣
b
⃗
∣
c
o
s
θ
\vec a *\vec b = |\vec a||\vec b|cos \theta
a∗b=∣a∣∣b∣cosθ
- Embedded Gaussian: 具体公式如下:
f ( x i , x j ) = e θ ( x i ) T ϕ ( x j ) C ( x ) = ∑ ∀ j f ( x i , x j ) f(x_i,x_j)=e^{\theta(x_i)^T\phi(x_j)} \\ C(x)=\sum_{\forall j}f(x_i,x_j) f(xi,xj)=eθ(xi)Tϕ(xj)C(x)=∀j∑f(xi,xj)
- Dot product: 具体公式如下:
f ( x i , x j ) = θ ( x i ) T ϕ ( x j ) C ( x ) = ∣ { i ∣ i i s a v a l i d i n d e x o f x } ∣ f(x_i,x_j)=\theta(x_i)^T\phi(x_j) \\ C(x)=|\{i|i is a valid index of x\}| f(xi,xj)=θ(xi)Tϕ(xj)C(x)=∣{i∣iisavalidindexofx}∣
- Concatenation: 具体公式如下:
f ( x i , x j ) = R e L U ( w f T . [ θ ( x i ) , ϕ ( x j ) ] ) C ( x ) = ∣ { i ∣ i i s a v a l i d i n d e x o f x } ∣ f(x_i,x_j)=ReLU(w_f^T .[\theta(x_i),\phi(x_j)]) \\ C(x)=|\{i|i is a valid index of x\}| f(xi,xj)=ReLU(wfT.[θ(xi),ϕ(xj)])C(x)=∣{i∣iisavalidindexofx}∣
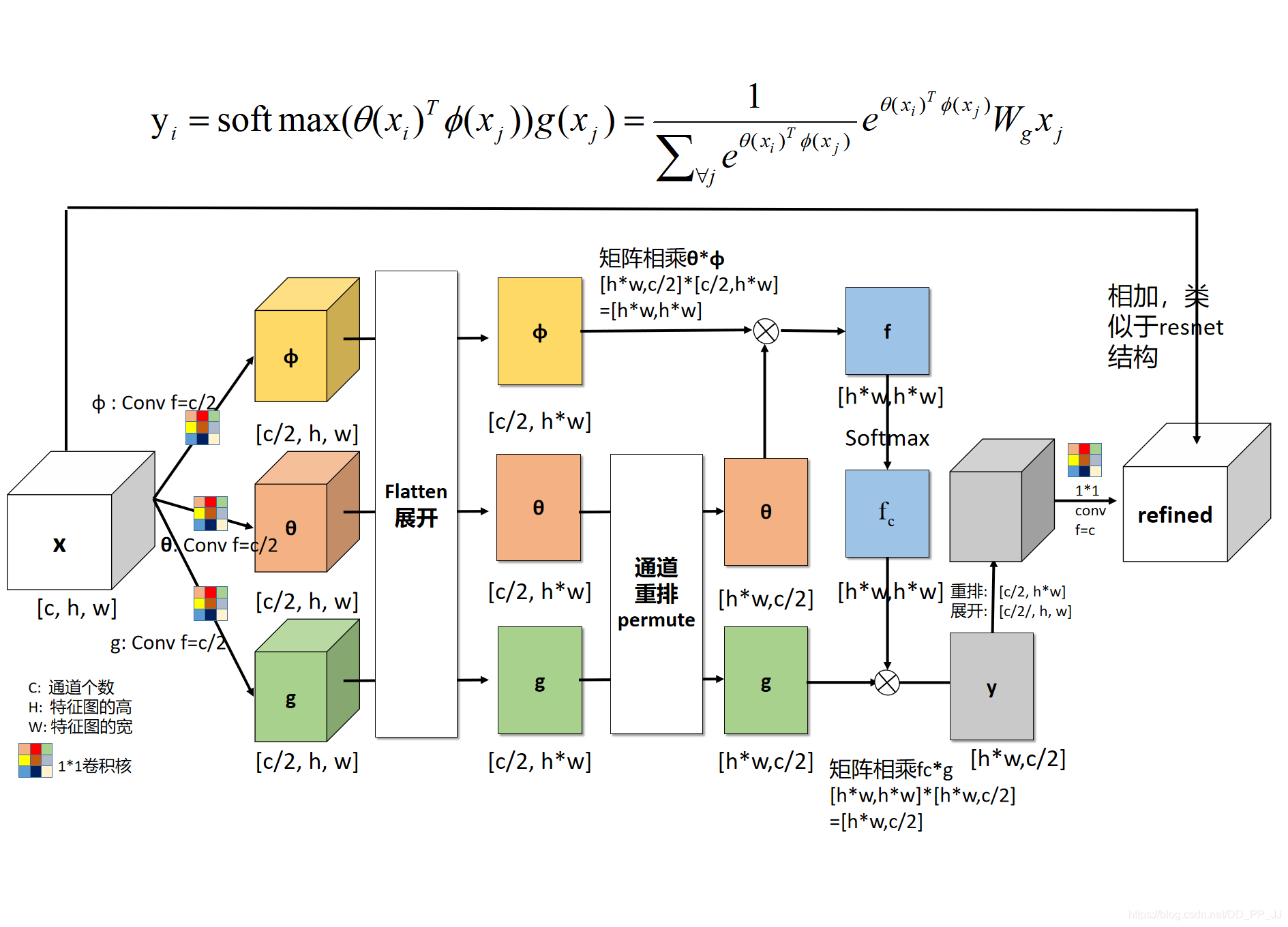
以上四个函数可能看起来感觉让人读起来很吃力,下边进行大概解释一下上边符号的意义,结合示意图(以Embeded Gaussian为例,对原图进行细节上加工,具体参见代码,地址为Github中的non_local_embedded_gaussian.py文件):
-
x代表feature map, x i x_i xi代表的是当前关注位置的信息; x j x_j xj代表的是全局信息。
-
θ代表的是 θ ( x i ) = W θ x i \theta (x_i)=W_{\theta}x_i θ(xi)=Wθxi ,实际操作是用一个1×1卷积进行学习的
-
φ代表的是 ϕ ( x j ) = W ϕ x j \phi (x_j)=W_{\phi}x_j ϕ(xj)=Wϕxj,实际操作是用一个1×1卷积进行学习的
-
g同理
-
C(x)代表的是归一化操作,在embedding gaussian中使用的是Sigmoid实现的。
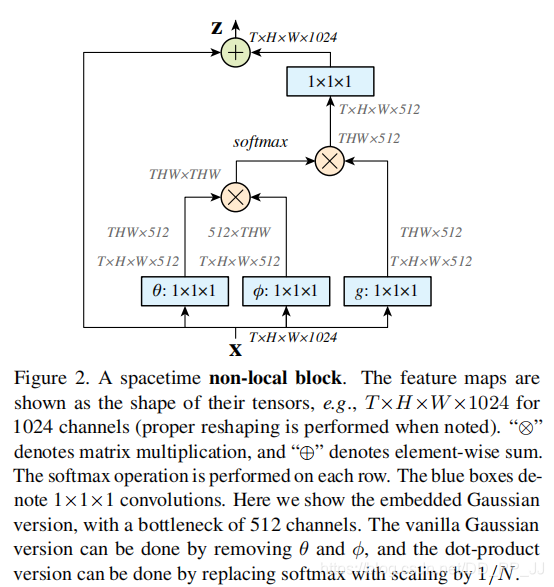
然后可以将上图(实现角度)与下图(比较抽象)进行结合理解:
具体解释如下:(ps: 以下解释带上了bs,上图中由于bs不方便画图,所以没有添加bs)
X是一个feature map,形状为[bs, c, h, w], 经过三个1×1卷积核,将通道缩减为原来一半(c/2)。然后将h,w两个维度进行flatten,变为h×w,最终形状为[bs, c/2, h×w]的tensor。对θ对应的tensor进行通道重排,在线性代数中也就是转置,得到形状为[bs, h×w, c/2]。然后与φ代表的tensor进行矩阵乘法,得到一个形状为[bs, h×w,h×w]的矩阵,这个矩阵计算的是相似度(或者理解为attention)。然后经过softmax进行归一化,然后将该得到的矩阵 f c f_c fc 与g 经过flatten和转置的结果进行矩阵相乘,得到的形状为[bs, h*w, c/2]的结果y。然后转置为[bs, c/2, h×w]的tensor, 然后将h×w维度重新伸展为[h, w],从而得到了形状为[bs, c/2, h, w]的tensor。然后对这个tensor再使用一个1×1卷积核,将通道扩展为原来的c,这样得到了[bs, c, h, w]的tensor,与初始X的形状是一致的。最终一步操作是将X与得到的tensor进行相加(类似resnet中的residual block)。
可能存在的问题
计算量偏大:在高阶语义层引入non local layer, 也可以在具体实现的过程中添加pooling层来进一步减少计算量。
3. 代码
代码来自官方,修改了一点点以便于理解,推荐将代码的forward部分与上图进行对照理解。
import torch
from torch import nn
from torch.nn import functional as F
class _NonLocalBlockND(nn.Module):
"""
调用过程
NONLocalBlock2D(in_channels=32),
super(NONLocalBlock2D, self).__init__(in_channels,
inter_channels=inter_channels,
dimension=2, sub_sample=sub_sample,
bn_layer=bn_layer)
"""
def __init__(self,
in_channels,
inter_channels=None,
dimension=3,
sub_sample=True,
bn_layer=True):
super(_NonLocalBlockND, self).__init__()
assert dimension in [1, 2, 3]
self.dimension = dimension
self.sub_sample = sub_sample
self.in_channels = in_channels
self.inter_channels = inter_channels
if self.inter_channels is None:
self.inter_channels = in_channels // 2
# 进行压缩得到channel个数
if self.inter_channels == 0:
self.inter_channels = 1
if dimension == 3:
conv_nd = nn.Conv3d
max_pool_layer = nn.MaxPool3d(kernel_size=(1, 2, 2))
bn = nn.BatchNorm3d
elif dimension == 2:
conv_nd = nn.Conv2d
max_pool_layer = nn.MaxPool2d(kernel_size=(2, 2))
bn = nn.BatchNorm2d
else:
conv_nd = nn.Conv1d
max_pool_layer = nn.MaxPool1d(kernel_size=(2))
bn = nn.BatchNorm1d
self.g = conv_nd(in_channels=self.in_channels,
out_channels=self.inter_channels,
kernel_size=1,
stride=1,
padding=0)
if bn_layer:
self.W = nn.Sequential(
conv_nd(in_channels=self.inter_channels,
out_channels=self.in_channels,
kernel_size=1,
stride=1,
padding=0), bn(self.in_channels))
nn.init.constant_(self.W[1].weight, 0)
nn.init.constant_(self.W[1].bias, 0)
else:
self.W = conv_nd(in_channels=self.inter_channels,
out_channels=self.in_channels,
kernel_size=1,
stride=1,
padding=0)
nn.init.constant_(self.W.weight, 0)
nn.init.constant_(self.W.bias, 0)
self.theta = conv_nd(in_channels=self.in_channels,
out_channels=self.inter_channels,
kernel_size=1,
stride=1,
padding=0)
self.phi = conv_nd(in_channels=self.in_channels,
out_channels=self.inter_channels,
kernel_size=1,
stride=1,
padding=0)
if sub_sample:
self.g = nn.Sequential(self.g, max_pool_layer)
self.phi = nn.Sequential(self.phi, max_pool_layer)
def forward(self, x):
'''
:param x: (b, c, h, w)
:return:
'''
batch_size = x.size(0)
g_x = self.g(x).view(batch_size, self.inter_channels, -1)#[bs, c, w*h]
g_x = g_x.permute(0, 2, 1)
theta_x = self.theta(x).view(batch_size, self.inter_channels, -1)
theta_x = theta_x.permute(0, 2, 1)
phi_x = self.phi(x).view(batch_size, self.inter_channels, -1)
f = torch.matmul(theta_x, phi_x)
print(f.shape)
f_div_C = F.softmax(f, dim=-1)
y = torch.matmul(f_div_C, g_x)
y = y.permute(0, 2, 1).contiguous()
y = y.view(batch_size, self.inter_channels, *x.size()[2:])
W_y = self.W(y)
z = W_y + x
return z
4. 实验结论
-
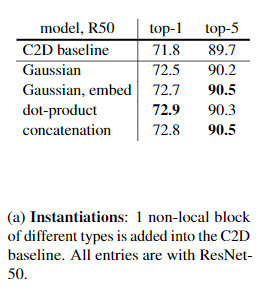
文中提出了四个计算相似度的模型,实验对四个方法都进行了实验,发现了这四个模型效果相差并不大,于是有一个结论:使用non-local对baseline结果是有提升的,但是不同相似度计算方法之间差距并不大,所以可以采用其中一个做实验即可,文中用embedding gaussian作为默认的相似度计算方法。
-
作者做了一系列消融实验来证明non local NN的有效性:
- 使用四个相似度计算模型,发现影响不大,但是都比baseline效果好。
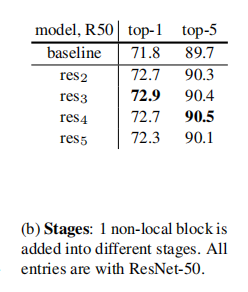
- 以ResNet50为例,测试加在不同stage下的结果。可以看出在res2,3,4部分得到的结果相对baseline提升比较大,但是res5就一般了,这有可能是由于第5个stage中的feature map的spatial size比较小,信息比较少,所以提升比较小。
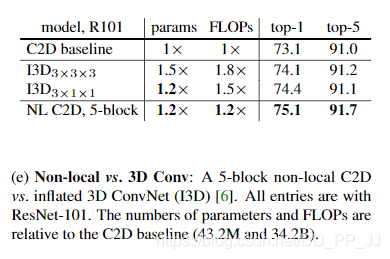
- 尝试添加不同数量的non local block ,结果如下。可以发现,添加越多的non local 模块,其效果越好,但是与此同时带来的计算量也会比较大,所以要对速度和精度进行权衡。
- Non-local 与3D卷积的对比,发现要比3D卷积计算量小的情况下,准确率有较为可观的提升。
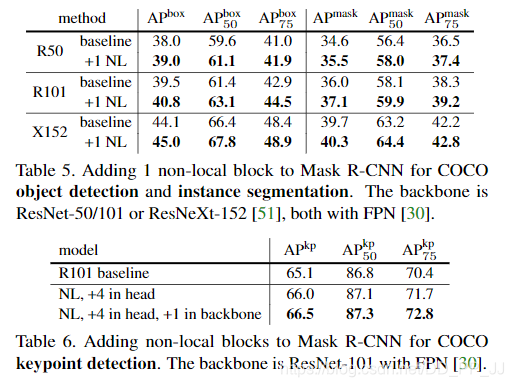
- 作者还将Non-local block应用在目标检测、实例分割、关键点检测等领域。可以将non-local block作为一个trick添加到目标检测、实例分割、关键点检测等领域, 可能带来1-3%的提升。
5. 评价
Non local NN从传统方法Non local means中获得灵感,然后接着在神经网络中应用了这个思想,直接融合了全局的信息,而不仅仅是通过堆叠多个卷积层获得较为全局的信息。这样可以为后边的层带来更为丰富的语义信息。
论文中也通过消融实验,完全证明了该模块在视频分类,目标检测,实例分割、关键点检测等领域的有效性,但是其中并没有给出其带来的参数量上的变化,或者计算速度的变化。但是可以猜得到,参数量的增加还是有一定的,如果对速度有要求的实验可能要进行速度和精度上的权衡,不能盲目添加non local block。神经网络中还有一个常见的操作也是利用的全局信息,那就是Linear层,全连接层将feature map上每一个点的信息都进行了融合,Linear可以看做一种特殊的Non local操作。
6. 参考内容
论文:https://arxiv.org/abs/1711.07971
video classification 代码:https://github.com/facebookresearch/video-nonlocal-net
non local官方实现:https://github.com/pprp/SimpleCVReproduction/tree/master/attention/Non-local/Non-Local_pytorch_0.4.1_to_1.1.0/lib
知乎文章:https://zhuanlan.zhihu.com/p/33345791
博客:https://hellozhaozheng.github.io/z_post/计算机视觉-NonLocal-CVPR2018/