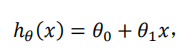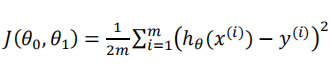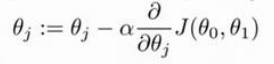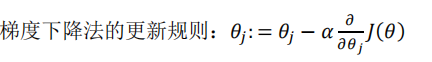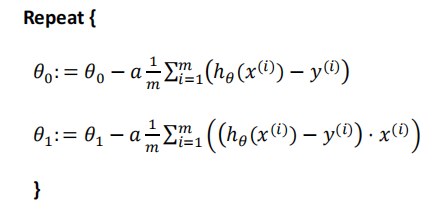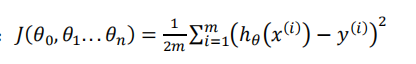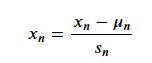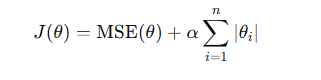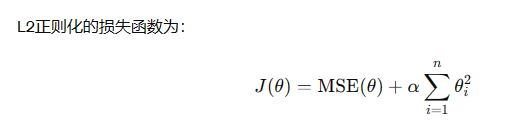机器学习-线性回归

文章目录

实现原理
梯度下架
多元化(泛化)
特征缩放
正归方程
经验
代码实现
线性回归的正则化

实现原理

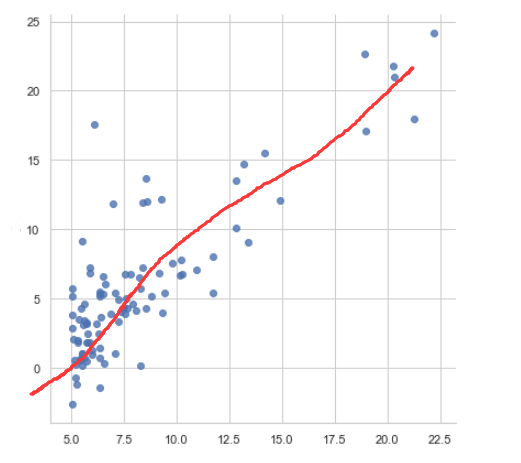
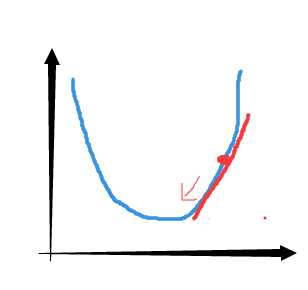
假设:我们可以用一个函数来模仿,现在数据的走势,比如以下的数据,假设我们有一个函数可以拟合,一下数据(红线).
在这里插入图片描述
我们先定义一个简单的函数,比如说是一元线性回归:
h: 表示我们预测的值
x: 变量
而我要求的就是这些参数.

但是如何能够准确的让我们模拟的函数准确呢?

我们再这里就利用了数学上的平方误差公式,然后利用方差公式,在求平方误差值最小的时候,我们的参数就是当前好的参数.
所以这里就引出了代价函数
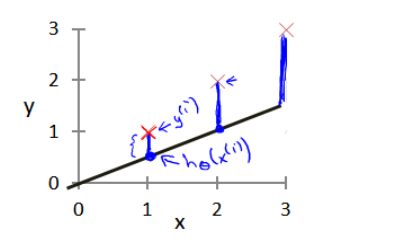
在这里插入图片描述
我们看红色X (真实值)距离我们自己画的函数有多远,尽量的让自己画的函数,能够挨着,真实值为最近.
(如何实现它能够尽量的接近呢? 我们就定义代价函数 – 基本的原理也是真实值与我们预测值的距离之和的平均值 ,)
在这里插入图片描述
注意: 上面之所以多除2 是因为后面比较好计算.

然后我们是怎么计算到这些值的呢?
就是求我们的代价函数最小值.
按数学的逻辑来说,我们就是要对我们的代价函数求导,要找到它的最小值,但是计算机如何做呢?

在这里插入图片描述

梯度下架

之前我们说了,要求代价函数的最小值,我们如何求呢?

现在就可以说了 ,我们是利用梯度下降算法来求到代价函数的最小值.

我们对代价函数求偏导,就能够得到梯度方向,然后就可以选择学习速率𝛼 ,
(一般是比较小的值),与它相乘. 然后在用原来的𝜃 减它,则可以得到一个新的𝜃.
一直这样迭代,就可以一直得到新的𝜃,直到找到代价函数最小时候的𝜃值.

梯度下降算法的每次迭代受到学习率的影响，如果学习率𝑎过小，则达到收敛所需的迭
代次数会非常高；如果学习率𝑎过大，每次迭代可能不会减小代价函数，可能会越过局部最
小值导致无法收敛。
通常可以考虑尝试些学习率：
𝛼 = 0.01，0.03，0.1，0.3，1，3，10

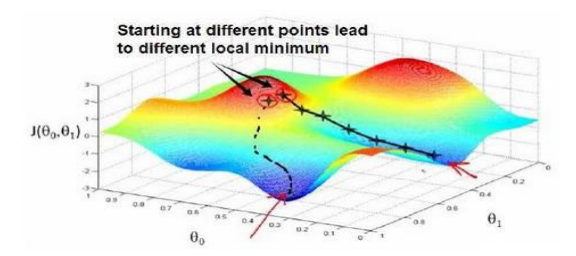
在这里插入图片描述

梯度下降背后的思想是：开始时我们随机选择一个参数的组合(𝜃0, 𝜃1, . . . . . . , 𝜃𝑛
)，计算代价函数，然后我们寻找下一个能让代价函数值下降最多的参数组合。我们持续这么做直到到
到一个局部最小值（local minimum），因为我们并没有尝试完所有的参数组合，所以不能确
定我们得到的局部最小值是否便是全局最小值（global minimum），选择不同的初始参数组
合，可能会找到不同的局部最小值。

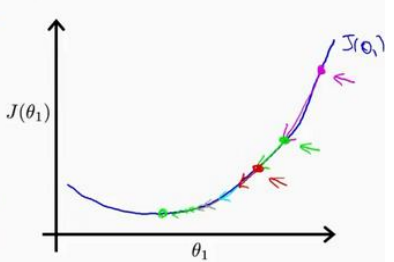
在这里插入图片描述

我想找到它的最小值，首先初始化我的梯度下降算法，在那个品红色的点初始化，如果我更新一步梯度下降，也许它会带我到这个点，因为这个点的导数是相当陡的。现在，在这个绿色的点，如果我再更新一步，你会发现我的导数，也即斜率，是没那么陡的。随着我接近最低点，我的导数越来越接近零，所以，梯度下降一步后，新的导数会变小一点点。然后我想再梯度下降一步，在这个绿点，我自然会用一个稍微跟刚才在那个品红点时比，再小一点的一步，到了新的红色点，更接近全局最低点了，因此这点的导数会比在绿点时更小。所以，我再进行一步梯度下降时，我的导数项是更小的，𝜃1更新的幅度就会更小。所以随着梯度下降法的运行，你移动的幅度会自动变得越来越小，直到最终移动幅度非常小，你会发现，已经收敛到局部极小值.

因为我们之前定义的两个参数 ,然后我们就需要一直迭代我们需要的两个参数,求到代价最少得时候两个参数的值.
在这里插入图片描述
这就叫做梯度下降.

然后你就可以联想到,如果是其他参数很多的时候这个时候你就可以把X 想象成一个向量,你自己也就可以拥有跟多的参数,而原理和上面的两个参数的原理也是一样的了.

多元化(泛化)

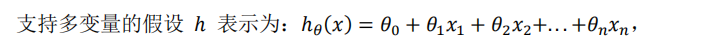
在这里插入图片描述多元的代价函数

和之前的算法一样一直迭代也就行了,之色只是这里用了一些数学上面的导数而已.

特征缩放

怎么说呢?如果有一个参数𝜃,它对我们的影响很大,就很多的影响算法,我们要想办法,面对多维特征问题的时候，我们要保证这些特征都具有相近的尺度，这将帮助梯度下降算法更快地收敛。
公式：
在这里插入图片描述
其中un是平均值，sn 是标准差。

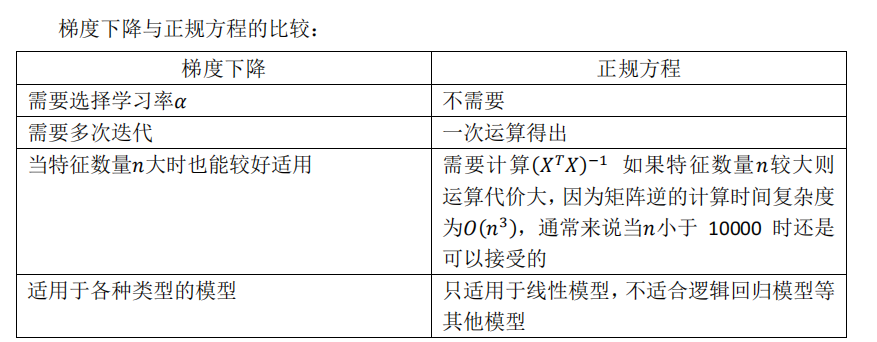
正归方程

在这里插入图片描述

经验

当一些指标比较少的时候可以取它们的平方啊
或者两个数值的乘法啊,等等
比如说有数据长 , 宽求房价 ,你可以再造一个数据长*宽 (面积)为新数据.

代码实现

from sklearn.linear_model import LinearRegression
import numpy as np
# 输入数据
X = np.array([[2104], [1600], [2400], [1416], [3000]])
y = np.array([399900, 329900, 369000, 232000, 539900])

# 创建线性回归模型
model = LinearRegression()

# 训练模型
model.fit(X, y)

# 打印参数
print("参数 theta：", model.intercept_, model.coef_[0])

# 预测
X_new = np.array([[1650]])
y_predict = model.predict(X_new)
print("预测价格：", y_predict[0])

线性回归的正则化

线性回归的正则化是通过在损失函数中添加正则化项来控制模型的复杂度，以防止过拟合。常用的两种正则化方法是L1正则化（Lasso）和L2正则化（Ridge）。

L1:损失函数为:

在这里插入图片描述

这里就避免了一些参数很大一些参数很小很小,能让他比较规整,的参数,正则化会让权重向量变得更加平滑，避免了特征权重过于剧烈变化，对异常值更加稳健。

from sklearn.linear_model import Ridge, Lasso

# 创建 Ridge 模型
ridge_model = Ridge(alpha=1.0)  # alpha 是正则化参数

# 创建 Lasso 模型
lasso_model = Lasso(alpha=1.0)

# 使用 Ridge 模型拟合数据
ridge_model.fit(X, y)

# 使用 Lasso 模型拟合数据
lasso_model.fit(X, y)

# 打印参数
print("Ridge 参数 theta：", ridge_model.intercept_, ridge_model.coef_)
print("Lasso 参数 theta：", lasso_model.intercept_, lasso_model.coef_)