前言
  🎄：CSDN的小伙伴们大家好，今天跟大家分享数据结构的知识——二叉树。如果这篇文章对你有用，麻烦给我点个小赞以示鼓励吧🎄
  🏡：博客主页：空山新雨后的java知识图书馆
  ☀️：天气很是炎热，想起来小时候的夏天，有冰棍。。。。
  📝:对于学者获得的成就，是恭维还是挑战?我需要的是后者，因为前者只能使人陶醉而后者却是鞭策。——巴斯德📝
  📖上一篇文章：SpringBoot基础📖
  👏欢迎大家一起学习，进步。加油👊

一、树

1.1、树的基本定义：

  树是我们计算机中非常重要的一种数据结构，同时使用树这种数据结构，可以描述现实生活中的很多事物，例如家谱、单位的组织架构、等等。

  树是由n（n>=1）个有限结点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。

1.2、树的特点

1.每个结点有零个或多个子结点；

2.没有父结点的结点为根结点；

3.每一个非根结点只有一个父结点；

4.每个结点及其后代结点整体上可以看做是一棵树，称为当前结点的父结点的一个子树；

1.3、树的相关术语

结点的度：

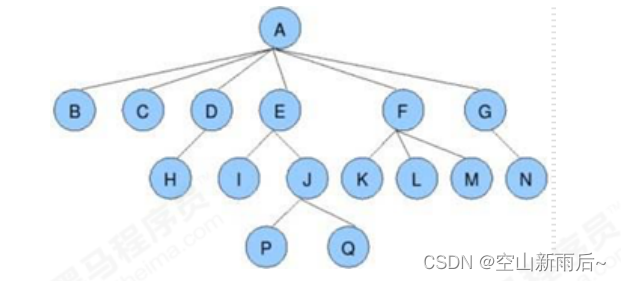
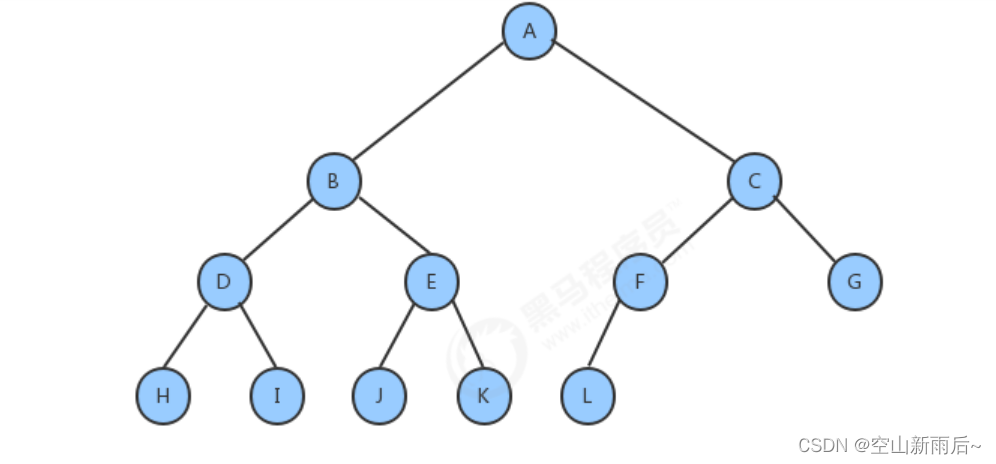
​   一个结点含有的子树的个数称为该结点的度。例如上图A结点的度为6，J结点的度为2。

叶子结点：

​   度为0的结点称为叶结点，也可以叫做终端结点。例如图中的B,C,H等结点。

分支结点：

  度不为0的结点称为分支节点，也可以叫做非终端结点。流入图中的D，E等结点。

结点的层次：

  从根节点开始，根节点的层次为1，根节点的直接后继层次为2，依次类推，图中有4层，J结点的层次为3。

结点的层序编号：

  将树中的结点，按照从上层到下层，同层从左到右的次序排成一个线性序列，把他们编成连续的自然数。 例如图中A，B,C,D,E的编号就是1,2,3,4,5.

树的度：

  树中所有结点的度的最大值。例如图中树的度为根节点的度为6。当然，并不是所有的树的度都是根节点的。要分具体情况。

树的高度：

  树中结点的最大层次，图中树的高度为4。

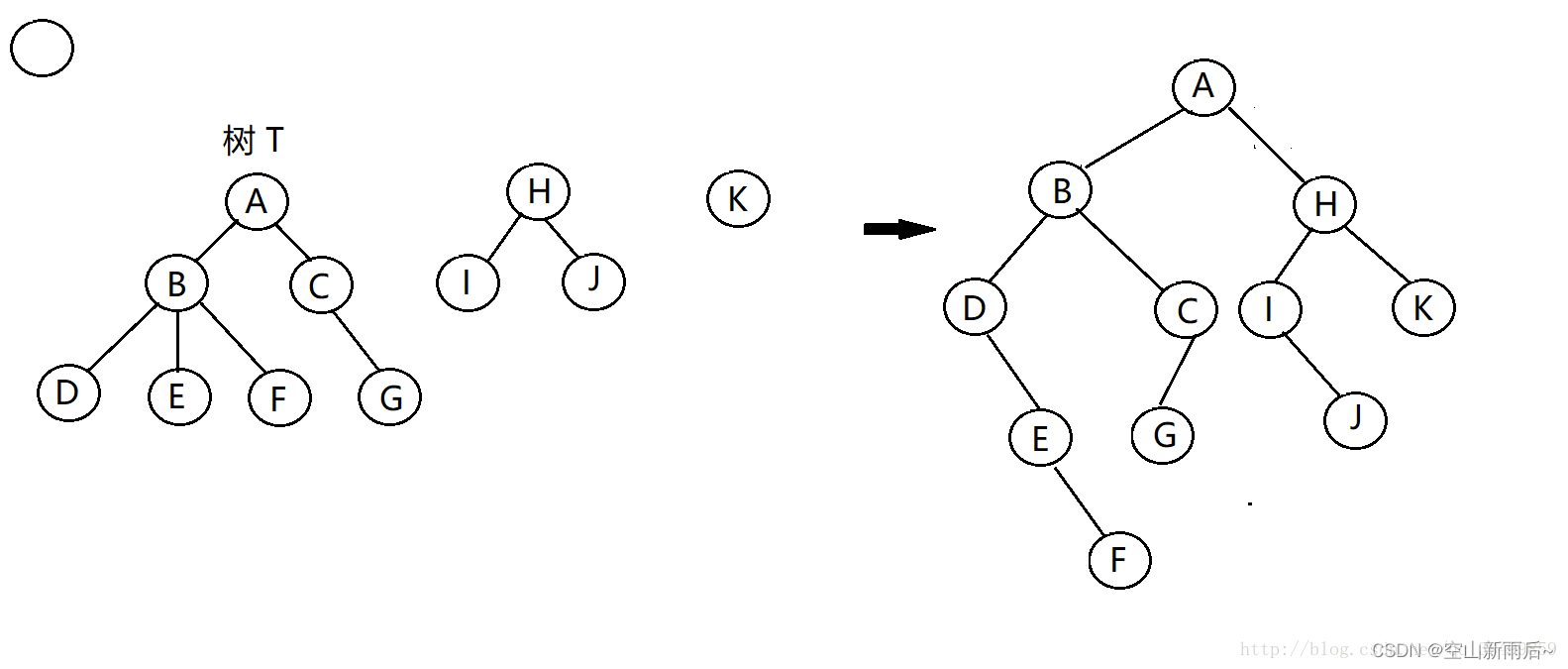
森林：

   m（m>=0）个互不相交的树的集合，将一颗非空树的根结点删去，树就变成一个森林；给森林增加一个统一的根结点，森林就变成一棵树

孩子结点：

​   一个结点的直接后继结点称为该结点的孩子结点。 例如H结点是D结点的孩子结点。I,J是E结点的孩子结点（用例为定义中的图）

双亲结点

​   一个结点的直接前趋称为该结点的双亲结点。

​ 例如E结点是I，J结点的双亲结点。

兄弟结点:
  同一个双亲结点的孩子结点间互称兄弟结点

​ 例如，I、J结点是兄弟结点。

路径：

​   从根结点到目标结点经过的结点，叫做路径，例如，A结点到Q结点的路径A,E,J,Q。

二、二叉树

2.1、二叉树的基本定义

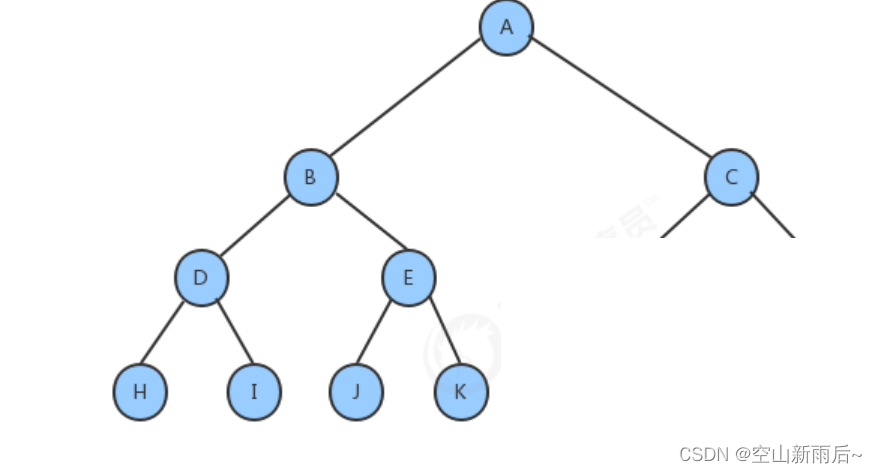
​   定义：二叉树就是度不超过2的树（每个结点最多只有两个子结点）也就是说，如果下图中D结点后面还跟一个结点，也就是说B结点还有一个孩子结点，那么这个树就不再是二叉树了。

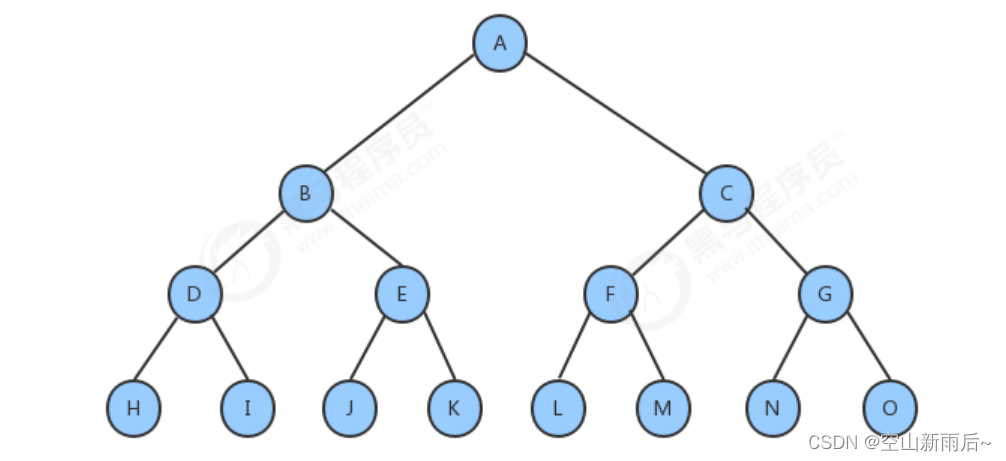
满二叉树：

​   一个二叉树，如果每一层的结点的树都达到最大值，那么这个二叉树就是满二叉树。也就是说这个二叉树的每一个结点都是两个，满足
$$每层结点=2^{k-1}$$
，（k是层数）那么这棵树就是满二叉树。

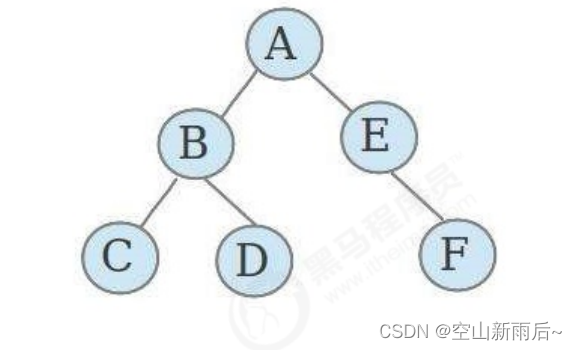
完全二叉树：

  叶节点只能出现在最下层和次下层，并且最下面一层的结点都集中在该层最左边的若干位置的二叉树

上图就是一个完全二叉树。

  而上图就不是一颗完全二叉树，因为他跳过了C结点，直接来到了A结点的次次结点。因此不是一个完全二叉树。

2.2、二叉树的简单增删改查操作

  树的前中后序遍历

  在写这个代码之前，我们必须了解二叉树的三种遍历方式
前序遍历：是先根结点，左子结点，然后再右子结点
中序遍历：先左子结点，根结点，然后再右子结点
后序遍历是：先左子结点，右子结点，最后才是根结点。

  那么了解到了二叉树的三种遍历方式之后，我们来举个例子

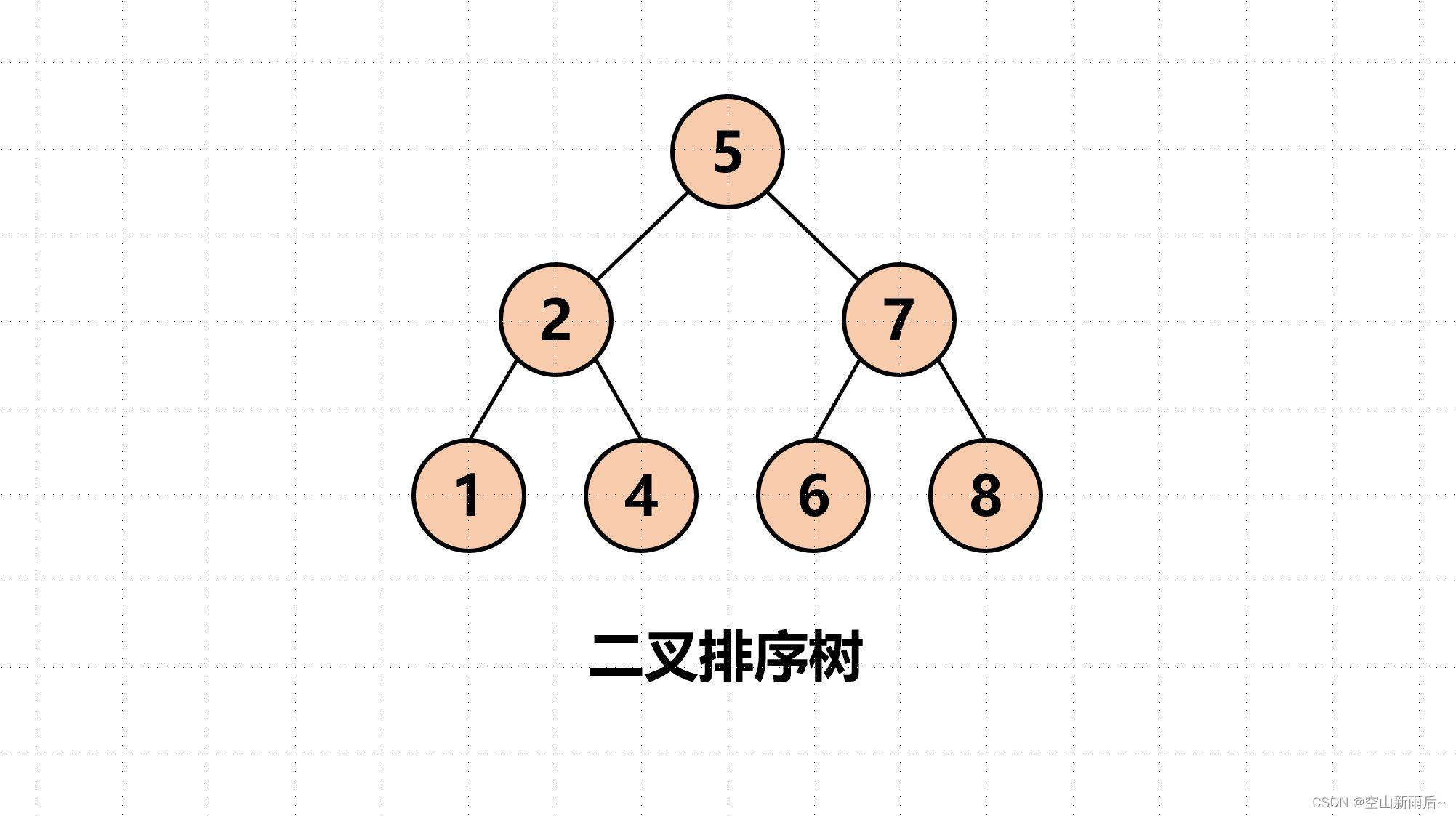
  例如这颗树，（如果这个图片挂了，大家可以在网上搜其他博主写的关于二叉树的前中后序遍历方式学习一下再来写这个代码。）
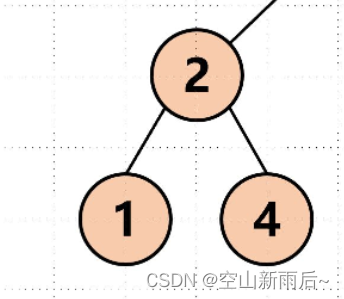
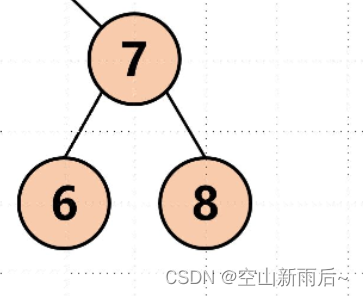
  那么按照刚刚讲的，前序遍历输出的话就应该先输出5，然后你可以将这颗树分为这样的就好理解了如下图↓，那么左边的子树就是2,1，4，根左右的顺序，右边的子树就是7.6.8，合起来这颗二叉树的
前序遍历顺序就是：5，2，1，4，7，6,8。
同理，中序遍历顺序就是：1、2、4、5、6、7、8.（左根右）
后续遍历顺序就是：1、4、2、6、8、7、5（左右根）

  2.2.1、结点Node类

package com.studySelf.tree.tree01;

/**
 * @author wang
 * @version 1.0
 * @packageName com.studySelf.tree.tree01
 * @className Node
 * @date 2022/4/19 20:15
 * @Description Node结点
 */
public class Node {
    //唯一编号
    private int num;
    //结点的值
    private String name;
    //左结点
    private Node left;
    //右节点
    private Node right;

    //构造方法

    public Node(int num, String name) {
        this.num = num;
        this.name = name;
    }

    public int getNum() {
        return num;
    }

    public void setNum(int num) {
        this.num = num;
    }

    public String getName() {
        return name;
    }

    public void setName(String name) {
        this.name = name;
    }

    public Node getLeft() {
        return left;
    }

    public void setLeft(Node left) {
        this.left = left;
    }

    public Node getRight() {
        return right;
    }

    public void setRight(Node right) {
        this.right = right;
    }

    @Override
    public String toString() {
        return "Node{" +
                "num=" + num +
                ", name='" + name + '\'' +
                ", left=" + left +
                ", right=" + right +
                '}';
    }

    /**
     * 前序遍历
     */
    public void preSelect() {
        //首先输出根结点
        System.out.println(this);
        //其次判断是否有左结点
        if (this.left != null) {
            //有左结点，就递归调用本方法输出该结点。
            this.left.preSelect();
        }
        //判断右节点，如果有，就递归输出
        if (this.right != null) {
            this.right.preSelect();
        }
    }

    /**
     * 中序遍历
     */
    public void infixSelect() {
        //首先判断左结点
        if (this.left != null) {
            //如果左结点不为空，递归向左子树调用
            this.left.infixSelect();
        }
        //当左结点为空，再输出根结点。当他本身就是最后一个左结点的时候，会直接输出，且没有右节点
        System.out.println(this);
        if (this.right != null) {
            //右节点同样如此，递归调用。直到没有结点为止。
            this.right.infixSelect();
        }
    }

    /**
     * 设二叉树有三个结点，根结点，左结点，右节点。
     * 后序遍历,解释，当一个二叉树的左结点不为空，那么他会进入下一个递归调用自己的后序遍历方法
     * 此时，根结点就是左结点，这时判断左结点，右节点均为空，就会输出左结点
     * 回退到根结点为this的时候，左结点已经判断完毕，接下来是右节点，右节点不为空，进入后续遍历递归，
     * 此时的this就是右节点，进入递归后，判断，不存在左右结点，输出this，也就是整个二叉树的右节点
     * 回退到this为根结点时，右节点也已经输出，走到最后一步，输出自己也就是this。
     * 整个后序遍历就结束，那么该二叉树的遍历结果就是左，右，根
     */

    public void afterSelect() {
        if (this.left != null) {
            this.left.afterSelect();
        }

        if (this.right != null) {
            this.right.afterSelect();
        }
        System.out.println(this);
    }

    /**
     * @param num
     * @Date 2022/4/21 17:51
     * @Param
     * @Return Node
     * @MetodName preSearchByNum
     * @Author wang
     * @Description 根据结点的编号来查询结点, 前序遍历查询，根，左，右
     */
    public Node preSearchByNum(int num) {
        //首先判断传进来的num与该结点的num是否相等
        //如果相等，那该结点就是我们要找的结点。
        if (this.num == num) {
            return this;
        }

        //如果不相等，该结点就不是我们要找的结点
        //那么我们就遍历该结点的左子节点，和右子结点
        //定义一个结点用于接收最后的返回结果
        Node resultNode = null;
        //如果该结点的左子结点不为空，就递归调用前序遍历，继续查找，如果找到了，那么resultNode就是我们想要的值
        if (this.left != null) {
            resultNode = this.left.preSearchByNum(num);
        }

        //如果遍历完左子结点，已经找到了我们想要的结果，直接返回结果即可，
        if (resultNode != null) {
            return resultNode;
        }

        //如果左子结点为空，且没有找到我们想要的结点的情况下。那就判断右子结点
        if (this.right != null) {
            resultNode = this.right.preSearchByNum(num);
        }
        //最后，如果找到了，那么resultNode一定会被赋值，如果没找到，就会返回null
        return resultNode;
    }

    /**
     * @param num
     * @Date 2022/4/21 17:58
     * @Param
     * @Return Node
     * @MetodName infixSearchByNum
     * @Author wang
     * @Description 中序遍历查找，左，根，右进行查询即可。
     */
    public Node infixSearchByNum(int num) {
        //首先判断左子结点,如果存在左子结点，递归继续查询遍历即可即可。
        Node resultNode = null;
        if (this.left != null) {
            resultNode = this.left.infixSearchByNum(num);
        }

        //如果左子结点已经找到了我们想要的结点，直接返回当前结点即可
        if (resultNode != null) {
            return resultNode;
        }

        //判断根结点
        if (this.num == num) {
            return this;
        }

        //判断右子结点，
        if (this.right != null) {
            resultNode = this.right.infixSearchByNum(num);
        }
        //最后返回我们的结果即可。
        return resultNode;
    }


    /**
     * @Date  2022/4/21 19:15
     * @Param
     * @param num
     * @Return Node
     * @MetodName afterSearchNum
     * @Author wang
     * @Description 后续遍历结点进行查找结点。左，右，根
     */
    public Node afterSearchNum(int num) {
        Node resultNode = null;
        //首先遍历左结点
        if (this.left != null) {
            resultNode = this.left.afterSearchNum(num);
        }

        //判断左结点是否找到哦啊
        if (resultNode != null) {
            return resultNode;
        }

        //判断右节点是否为空
        if (this.right != null) {
            resultNode = this.right.afterSearchNum(num);
        }

        //判断右节点是否找到
        if (resultNode != null) {
            return resultNode;
        }

        //判断根结点是否为我们找的结点
        if (this.num == num){
            return this;
        }
        //最后返回
        return resultNode;
    }

    /**
     * @Date  2022/4/25 19:30
     * @Param
     * @param num
     * @Return void
     * @MetodName delNodeByNum
     * @Author wang
     * @Description 根据结点的编号删除结点
     */
    public void delNodeByNum(int num) {
        //首先，判断当前结点的左结点是否为空，并且左结点的num是否与num相等
        if (this.left != null && this.left.num == num) {
            //如果相等，那就说明该结点就是我们要删除的结点,将其左结点置空即可
            this.left = null;
            return;
        }

        //如果左结点没有执行，说明左结点没有我们想要的结果，也就是要删除的结点不在左结点
        //那么就对右节点进行判断
        if (this.right != null && this.right.num == num) {
            this.right = null;
            return;
        }

        //如果左右结点均没有找到目标结点
        //那么就对左子树进行递归删除操作
        if (this.left != null) {
            this.left.delNodeByNum(num);
        }

        //同理，如果左子树没有目标结点，向右子树进行递归删除操作
        if (this.right != null) {
            this.right.delNodeByNum(num);
        }

    }
}

  2.2.2、二叉树结点类

package com.studySelf.tree.tree01;

/**
 * @author wang
 * @version 1.0
 * @packageName com.studySelf.tree.tree01
 * @className BinaryTree
 * @date 2022/4/20 20:29
 * @Description 二叉树的实体类
 */
public class BinaryTree {
    private Node root;//根结点
    //给某一个结点设置根结点的方法
    public void setRoot(Node node){
        this.root = node;
    }

    /**
     * 前序遍历二叉树
     */
    public void preSelect() {
        if (this.root != null) {
            this.root.preSelect();
        }else {
            System.out.println("该二叉树为空");
        }
    }

    /**
     * 中序遍历二叉树
     */

    public void infixSelect() {
        if (this.root != null) {
            this.root.infixSelect();
        }else {
            System.out.println("该二叉树为空");
        }

    }

    /**
     * 后序遍历二叉树
     */
    public void afterSelect() {
        if (this.root != null) {
            this.root.afterSelect();
        }else {
            System.out.println("该二叉树为空");
        }
    }


    /**
     * 根据id查询二叉树的结点，前序遍历
     */
    public Node preFindNodeByNum(int num){
        if (this.root !=null) {
            return this.root.preSearchByNum(num);
        }else {
            System.out.println("二叉树为空，无法查询");
            return null;
        }
    }

    /**
     * 根据id查询二叉树的结点，中序遍历方式
     */

    public Node infixFindNodeByNum(int num) {
        if (this.root != null) {
            return this.root.infixSearchByNum(num);
        }else {
            System.out.println("二叉树为空，无法查询");
            return null;
        }
    }

    /**
     * 根据id查询二叉树的结点，中序遍历方式
     * @param num
     * @return
     */
    public Node afterFindNodeByNum(int num) {
        if (this.root != null) {
            return this.root.afterSearchNum(num);
        }else {
            System.out.println("二叉树为空，无法查询");
            return null;
        }
    }

    /**
     * @Date  2022/4/25 19:36
     * @Param
     * @param num
     * @Return void
     * @MetodName deleteNodeByNum
     * @Author wang
     * @Description 根据二叉树结点的num删除结点
     */
    public void deleteNodeByNum(int num) {
        //首先判断二叉树不为空
        if (root != null) {
            //如果二叉树的根结点的值就是我们要删除的值
            if (root.getNum() == num) {
                root = null;
            }else {
                //如果不是根结点，就是对各个结点进行删除
                root.delNodeByNum(num);
            }
        }else {
            //二叉树根结点为空，那么直接返回
            System.out.println("二叉树为空，无法进行删除操作");
            return;
        }
    }
}

  那么二叉树的查询遍历等方法代码我已经写好了，并且整理好了，并且给了注释，大家可以自行理解，不懂的地方可以评论区指出哦。主要就是善用递归。然后利用二叉树的前中后序的遍历思想，就可以对二叉树进行遍历了。
测试类

package com.studySelf.tree.tree01;

import org.junit.Test;

import java.lang.reflect.Array;

/**
 * @author wang
 * @version 1.0
 * @packageName com.studySelf.tree.tree01
 * @className BinaryTreeTest
 * @date 2022/4/21 16:13
 * @Description 二叉树的测试类
 */
public class BinaryTreeTest {

    public static void main(String[] args) {
        //定义结点
        Node root = new Node(1, "刘备");
        Node node2 = new Node(2, "关羽");
        Node node3 = new Node(3, "张飞");
        Node node4 = new Node(4, "赵云");
        Node node5 = new Node(5, "黄忠");
        Node node6 = new Node(6, "马超");
        Node node7 = new Node(7, "阿斗");

        //给结点赋值关系，形成一颗二叉树
        root.setLeft(node2);
        root.setRight(node3);
        node3.setLeft(node4);
        node3.setRight(node5);
        node2.setRight(node6);
        node2.setLeft(node7);


        //定义一个二叉树，给定一个根结点。
        BinaryTree binaryTree = new BinaryTree();
        binaryTree.setRoot(root);

        //前序遍历
        binaryTree.preSelect();
        System.out.println("================================================");
        /*Node{num=1, name='刘备', left=Node{num=2, name='关羽', left=Node{num=7, name='阿斗', left=null, right=null}, right=Node{num=6, name='马超', left=null, right=null}}, right=Node{num=3, name='张飞', left=Node{num=4, name='赵云', left=null, right=null}, right=Node{num=5, name='黄忠', left=null, right=null}}}
Node{num=2, name='关羽', left=Node{num=7, name='阿斗', left=null, right=null}, right=Node{num=6, name='马超', left=null, right=null}}
Node{num=7, name='阿斗', left=null, right=null}
Node{num=6, name='马超', left=null, right=null}
Node{num=3, name='张飞', left=Node{num=4, name='赵云', left=null, right=null}, right=Node{num=5, name='黄忠', left=null, right=null}}
Node{num=4, name='赵云', left=null, right=null}
Node{num=5, name='黄忠', left=null, right=null}
*/
        //中序遍历
        binaryTree.infixSelect();
/*
* Node{num=7, name='阿斗', left=null, right=null}
Node{num=2, name='关羽', left=Node{num=7, name='阿斗', left=null, right=null}, right=Node{num=6, name='马超', left=null, right=null}}
Node{num=6, name='马超', left=null, right=null}
Node{num=1, name='刘备', left=Node{num=2, name='关羽', left=Node{num=7, name='阿斗', left=null, right=null}, right=Node{num=6, name='马超', left=null, right=null}}, right=Node{num=3, name='张飞', left=Node{num=4, name='赵云', left=null, right=null}, right=Node{num=5, name='黄忠', left=null, right=null}}}
Node{num=4, name='赵云', left=null, right=null}
Node{num=3, name='张飞', left=Node{num=4, name='赵云', left=null, right=null}, right=Node{num=5, name='黄忠', left=null, right=null}}
Node{num=5, name='黄忠', left=null, right=null}*/
        System.out.println("================================================");
        //后序遍历
        binaryTree.afterSelect();
/*
* Node{num=7, name='阿斗', left=null, right=null}
Node{num=6, name='马超', left=null, right=null}
Node{num=2, name='关羽', left=Node{num=7, name='阿斗', left=null, right=null}, right=Node{num=6, name='马超', left=null, right=null}}
Node{num=4, name='赵云', left=null, right=null}
Node{num=5, name='黄忠', left=null, right=null}
Node{num=3, name='张飞', left=Node{num=4, name='赵云', left=null, right=null}, right=Node{num=5, name='黄忠', left=null, right=null}}
Node{num=1, name='刘备', left=Node{num=2, name='关羽', left=Node{num=7, name='阿斗', left=null, right=null}, right=Node{num=6, name='马超', left=null, right=null}}, right=Node{num=3, name='张飞', left=Node{num=4, name='赵云', left=null, right=null}, right=Node{num=5, name='黄忠', left=null, right=null}}}
*/


    }


    /**
     * @Date 2022/4/21 19:45
     * @Param
     * @Return void
     * @MetodName testFind
     * @Author wang
     * @Description 测试二叉树的结点根据id查询的方法
     */
    @Test
    public void testFind() {
        //定义结点
        Node root = new Node(1, "刘备");
        Node node2 = new Node(2, "关羽");
        Node node3 = new Node(3, "张飞");
        Node node4 = new Node(4, "赵云");
        Node node5 = new Node(5, "黄忠");
        Node node6 = new Node(6, "马超");
        Node node7 = new Node(7, "阿斗");

        //给结点赋值关系，形成一颗二叉树
        root.setLeft(node2);
        root.setRight(node3);
        node3.setLeft(node4);
        node3.setRight(node5);
        node2.setRight(node6);
        node2.setLeft(node7);


        BinaryTree binaryTree = new BinaryTree();
        binaryTree.setRoot(root);

        Node preNode = binaryTree.preFindNodeByNum(2);
        System.out.println(preNode.getNum() + preNode.getName());

        Node infixNode = binaryTree.infixFindNodeByNum(2);
        System.out.println(infixNode.getNum() + infixNode.getName());

        Node afterNode = binaryTree.afterFindNodeByNum(2);
        System.out.println(afterNode.getNum() + afterNode.getName());

      /*查到的结果都是一样的说明没有错
        2关羽
        2关羽
        2关羽*/
    }


    /**
     * @Date  2022/4/25 19:39
     * @Param
     * @Return void
     * @MetodName testDel
     * @Author wang
     * @Description 测试二叉树的结点的删除
     */
    @Test
    public void testDel() {
        //定义结点
        Node root = new Node(1, "刘备");
        Node node2 = new Node(2, "关羽");
        Node node3 = new Node(3, "张飞");
        Node node4 = new Node(4, "赵云");
        Node node5 = new Node(5, "黄忠");
        Node node6 = new Node(6, "马超");
        Node node7 = new Node(7, "阿斗");

        //给结点赋值关系，形成一颗二叉树
        root.setLeft(node2);
        root.setRight(node3);
        node3.setLeft(node4);
        node3.setRight(node5);
        node2.setRight(node6);
        node2.setLeft(node7);


        BinaryTree binaryTree = new BinaryTree();
        binaryTree.setRoot(root);

        binaryTree.deleteNodeByNum(3);
        binaryTree.preSelect();
        System.out.println("=============");
/*Node{num=1, name='刘备', left=Node{num=2, name='关羽', left=Node{num=7, name='阿斗', left=null, right=null}, right=Node{num=6, name='马超', left=null, right=null}}, right=null}
Node{num=2, name='关羽', left=Node{num=7, name='阿斗', left=null, right=null}, right=Node{num=6, name='马超', left=null, right=null}}
Node{num=7, name='阿斗', left=null, right=null}
Node{num=6, name='马超', left=null, right=null}
=============*/
        /*可以见到结点三以及他的左右结点都已经被删除*/


    }

2.3、顺序存储二叉树

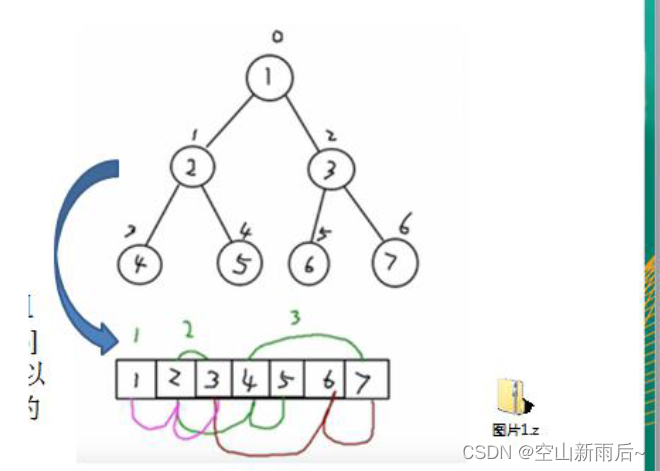
  从数据存储来看，数组存储方式和树的存储方式可以相互转换，即数组可以转换成树，树也可以转换成数组

  2.3.1、顺序存储二叉树的特点

1) 顺序二叉树通常只考虑完全二叉树
2) 第 n 个元素的左子节点为 2 * n + 1
3) 第 n 个元素的右子节点为 2 * n + 2
4) 第 n 个元素的父节点为 (n-1) / 2
5) n : 表示二叉树中的第几个元素(按 0 开始编号如图所示)

那么要求将二叉树的结点按照前中后序遍历出来

  2.3.2、顺序存储二叉树代码实现

顺序存储二叉树结点类

package com.studySelf.tree.tree01;

/**
 * @author wang
 * @version 1.0
 * @packageName com.studySelf.tree.tree01
 * @className ArrayBinaryTree
 * @date 2022/4/25 20:08
 * @Description 顺序存储二叉树，用arr数组进行存储
 */
public class ArrayBinaryTree {
    /**
     * 传入的二叉树存储数组
     */
    private int[] arrays;

    public ArrayBinaryTree(int[] arrays) {
        this.arrays = arrays;
    }

    /**
     * @Date 2022/4/26 19:57
     * @Param
     * @Return void
     * @MetodName preSelect
     * @Author wang
     * @Description 重载的前序遍历顺序二叉树的方法，因为默认从根节点开始遍历
     */
    public void preSelect() {
        this.preSelect(0);
    }

    public void infixSelect() {
        this.infixSelect(0);
    }

    public void postSelect() {
        this.postSelect(0);
    }

    /**
     * @param index 传入的二叉树的在数组中的下标
     * @Date 2022/4/26 19:58
     * @Param
     * @Return void
     * @MetodName preSelect
     * @Author wang
     * @Description 前序遍历顺序二叉树的方法
     */
    public void preSelect(int index) {
        /*首先判断数组也就是二叉树不能为空*/
        if (arrays == null || arrays.length == 0) {
            System.out.println("顺序二叉树为空");
            return;
        }
        /*前序遍历，如果不为空，那么就会先输出根节点*/
        System.out.print(arrays[index] + ",\t");

        /*其次根据顺序二叉树的特点，递归遍历顺序二叉树的左子树
         * 遍历的前提是左子树得有值，也就是推算出来的左子树的左结点的下标他不能超过数组也就是
         * 顺序二叉树的长度。*/
        if ((index * 2 + 1) < arrays.length) {
            preSelect(index * 2 + 1);
        }

        /*再然后就是递归遍历右子树，同样利用顺序二叉树本身的特点。*/
        if ((index * 2 + 2) < arrays.length) {
            preSelect(index * 2 + 2);
        }
    }

    /**
     * @param index 传入的二叉树的在数组中的下标
     * @Date 2022/4/26 20:02
     * @Param
     * @Return void
     * @MetodName infixSelect
     * @Author wang
     * @Description 中序遍历顺序二叉树
     */
    public void infixSelect(int index) {
        /*首先依旧是判断二叉树不为空*/
        if (arrays == null || arrays.length == 0) {
            System.out.println("顺序二叉树为空");
            return;
        }

        /*如果不为空，中序遍历首先应该遍历左子树*/
        if ((index * 2 + 1) < arrays.length) {
            infixSelect((index * 2 + 1));
        }

        /*遍历完左子树就会到根结点*/
        System.out.print(arrays[index] + ",\t");

        /*接下来就是遍历右子树的结点*/
        if ((index * 2 + 2) < arrays.length) {
            infixSelect((index * 2 + 2));
        }

    }

    /**
     * @param index 传入的二叉树的在数组中的下标
     * @Date 2022/4/26 20:10
     * @Param
     * @Return void
     * @MetodName postSelect
     * @Author wang
     * @Description 后续遍历顺序二叉树
     */
    public void postSelect(int index) {
        /*首先判断二叉树或者数组是否为空*/
        if (arrays == null || arrays.length == 0) {
            System.out.println("顺序二叉树为空");
            return;
        }

        /*如果不为空，后续遍历，先递归遍历左子树*/
        if ((index * 2 + 1) < arrays.length) {
            postSelect((index * 2 + 1));
        }

        /*再递归遍历右子树。*/
        if ((index * 2 + 2) < arrays.length) {
            postSelect((index * 2 + 2));
        }

        /*最后输出根结点*/
        System.out.print(arrays[index] + ",\t");
    }
}

测试类

@Test
public void test() {
    int[] arrays = {1,2,3,4,5,6,7};
    ArrayBinaryTree arrayBinaryTree = new ArrayBinaryTree(arrays);
    arrayBinaryTree.preSelect();

    System.out.println( );
    System.out.println("========");
    arrayBinaryTree.infixSelect();
    System.out.println( );
    System.out.println("========");
    arrayBinaryTree.postSelect();
    
    //1,	2,	4,	5,	3,	6,	7,	
    //========
    //4,	2,	5,	1,	6,	3,	7,	
    //========
    //4,	5,	2,	6,	7,	3,	1,	
}