Bite,Byte and Integers
19世纪Algebraic通过发出机械噪音的设备实现了逻辑,具体如下
具体到计算机中
正如书上例子01101001 变成{0,3,5,6} 01010101是{0,2,4,6} 76543210 76543210 体现了一个字节表示八种情况,在IO流中体现;不同的网络连接有一个输入;某个数据结构隐藏在可视库调用
最后一行真的nb :p&&*p避免nullptr
这里返回1的原因是这里的两个条件都是真,所以这不是位操作。而是判断“真”“假”,但是当它返回“真”时返回的是1。而不是你给出的任何数字,显然这和位操作完全不同,但是这种情况在你你一时疏忽,或者误操作时很容易出现,特别是提前终止”这种特性被很多人用到的时候,如果你想确保你没有访问空指针,你可以在访问它之前先测试它是否为空指针,如果这是0或,能避免对null的引用,所以无论如何,在这个层面上。我们大多数都是看比特
shift
左移总是相同的,但是右移有两种不同方式,逻辑移位,算术移位,详细见书
what happen if 把8位数字左移8位?x<<8:实际上 应该得到的还是原来的数字,本来就是8位,左移8位就是不移,这里的 观察低的3个比特是 位移量的3个比特,不是操作数,也就是你要移动8或7,或者18,这些数的二进制的低3位,就像模8(2^3)一样。第三版书P41旁注有具体说明,书上讲的很详细,当移动 k 位时,数据类型为 w 位,实际位移量为 k mod w。假设一个数据类型总共8位,则如果移动的位数超过8位,原有的数据就都移没了,编译器为了防止这种情况发生,会将你要移动的位数对8进行取模,以保证不会将原有的数据全部移没了
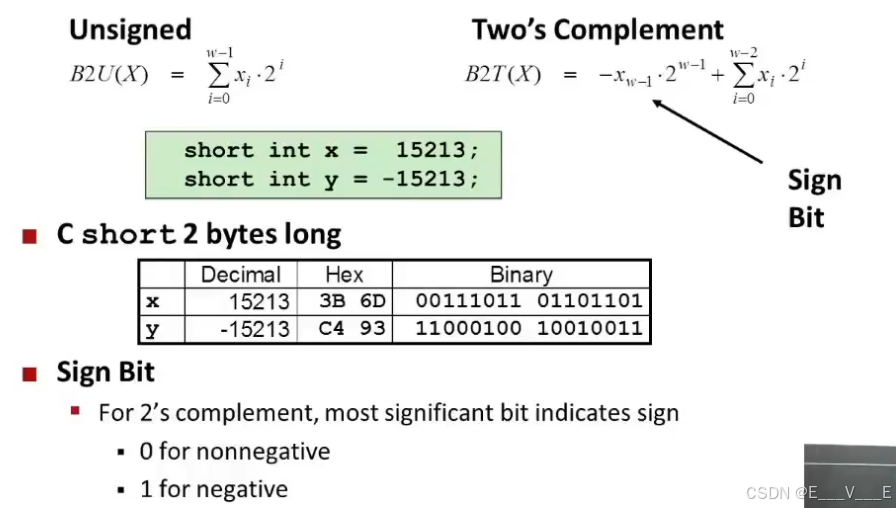
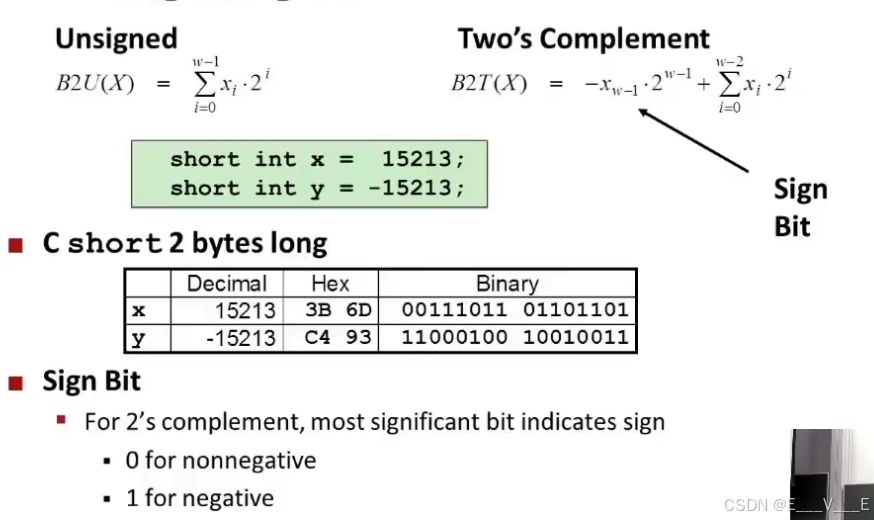
这是另一种补码的数学思考方式
所以一个是如果你有一个无符号的数字,如果你有一个无符号的数字,那么这只是转换,的意思是从比特位模式转化成无符号数的编码表示,意思是我们将加权位求和(看屏幕左上角那个公式),每个比特用2的来加权,当我们看补码的时候和无符号数唯一的区别就是,可以表示负数,最重要的一点是所谓的符号位(-)第一行表示从低到高的位数,第二行表示仅当这一位是1时对应的数值。
4 3 2 1 0 16 8 4 2 1对于01101就是8+4+1=13,10110是16+4+2=22
有符号时,????????
因此,最高位有时称为符号位 如果它是1,则该数字将是负数
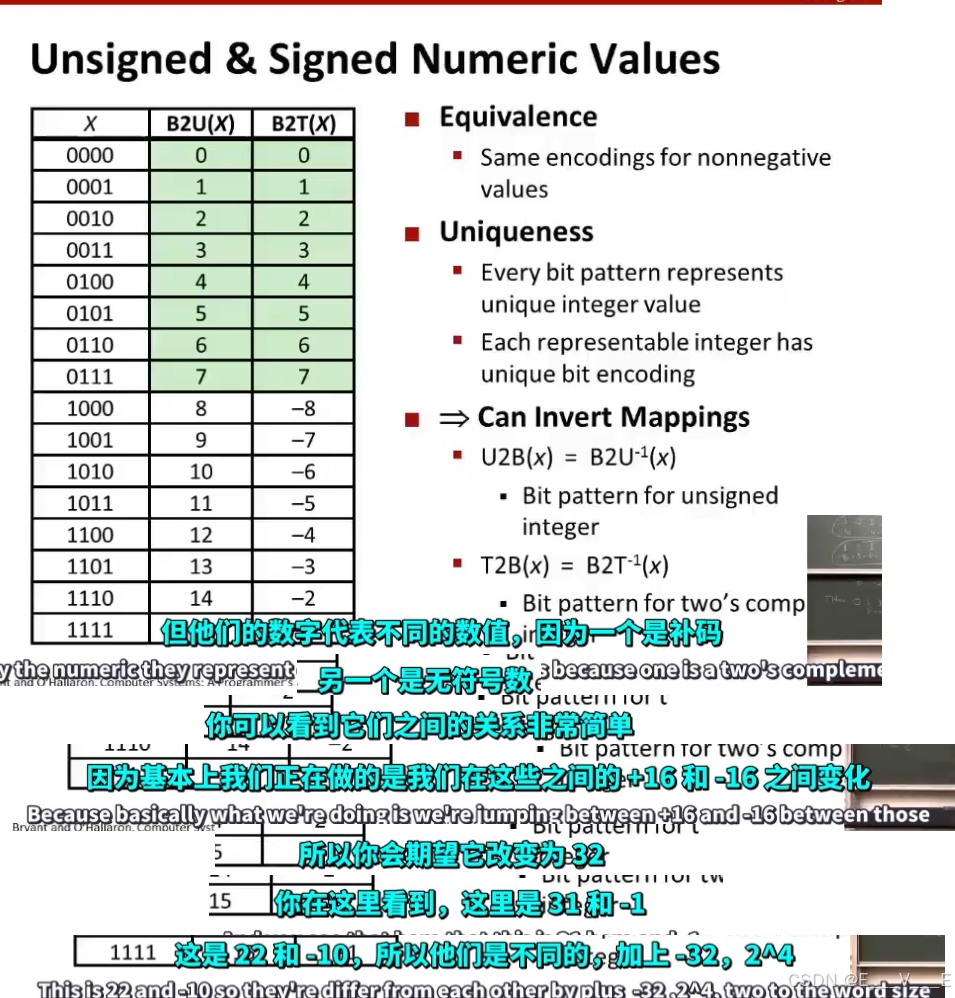
所以显然,如果这些都是零,我能得到0 如果全是1,那么将是16+8+4+2+1将是31 ,但是补码-16+8+4+2+1=-1,所有的都是负数-1
有一个独特的数字代表
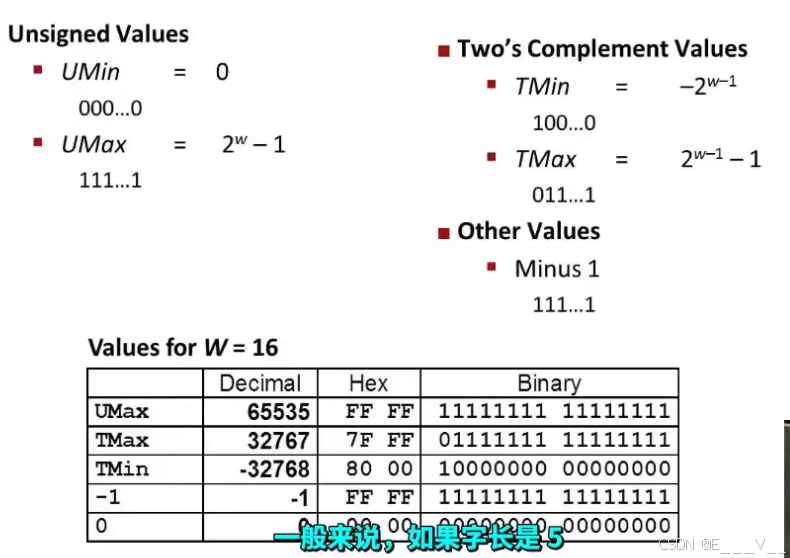
从10000(min)到11111(-1)到00000(0)到01111(max)
这些数字中UMax最大的无符号数字
TMin是补码的最小值
TMax是补码的最大值
此图表显示了不同字长数值的范围
但是在c中无符号数和补码中跳来跳去,尤其是一些特别大的数字,他说无符号数,结果突然变成负数,因为他被以为是补码
如果我们使用一个4位的数值模式
我们写出所有可能的值都是无符号或二进制补码
那么在最高位是0的情况下,两种表示方式的值是相同的
在这种情况下,最高位是1,它们将相差16,2^4
注意有些数是唯一的。对于给定范围的任何数字都有一个唯一的位模式
在计算机上本身并不知道是否给定位模式
你正在考虑作为一个负数或二进制补码,它只是一堆比特
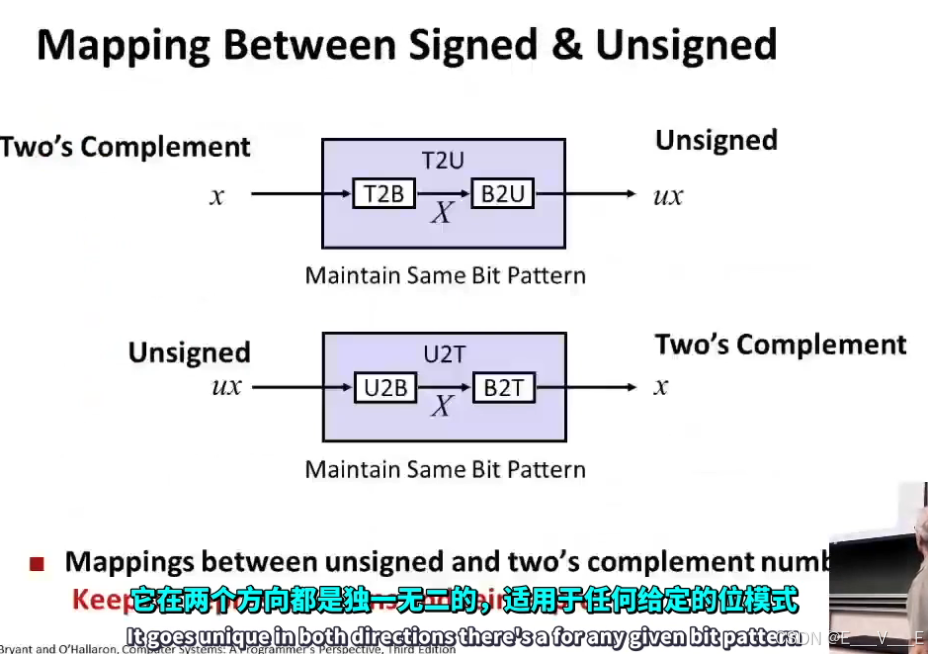
同样。我们可以在补码和无符号二进制之间来回保持位模式相同
所以当我从signed到unsigned二进制补码无符号时,我会调用该T2U
如果我从unsigned到signed我会调用U2T(3张ppt连用)
正如我提到的最高位是1的数字的区别
莱以一个因子2^w,其中w是字长
Lecture 02 Bits, Bytes, and Integer_哔哩哔哩_bilibili到41.33对那张红绿相间对照图做了阐述,书上有详细的转化过程,依据是从前面的B2T、B2U而来
第五组:当我减去时,你可以认为他是负的TMax-1,就变成TMin,所以相比较大小,这个首位不是一个负权重,而是正的,
太长了!!!!!忘记看到哪了
请把书看一遍!
补码的算术运算
对于无符号整数,现在有4位数表示范围在0到2^4-1之间。我们计算13+5,就是1101+0101=10010,把前面的1丢弃认为是0010,即2.
对于补码,1101+0101(即-3+5)得到00010同理是2,巧妙在于负数用ppt右上角公式计算,1011+0011(即-5+3=-2),那么补码溢出会?称为负溢出。那么对于两正得负称为正溢出。
14.30的ppt图片
对于无符号数的乘法,如计算5*5得到9,同样是因为高位丢弃,最高位无论什么都可以,不论符号。我们在二进制中左移k位,就乘2^k,右移同理的是除以。
我们举一个例子0110即6,右移是0011即3,右移0001即1,发现向下取舍
那对于负数移位时,有两种移位方法,逻辑移位和算术移位(逻辑移位用0,算术移位以1填充)如1010是-6右移一位是1101即-1,这时不能右移啦,在执行除以2^k的移位前,加一个偏移量(这里是1)于是原本变成1110即-2.现在是1111即-1
31.42开始进行详细阐述
Floating Point
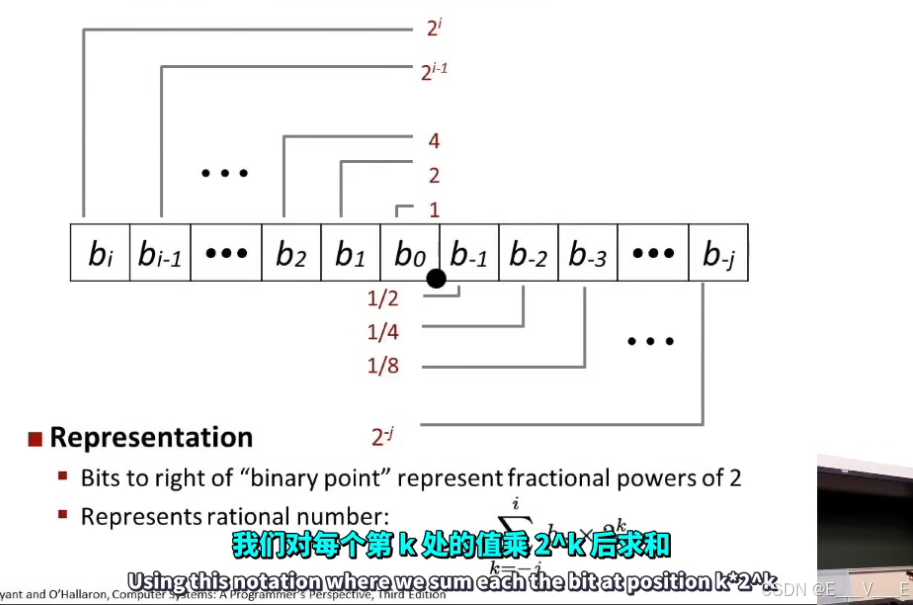
所以5又3/4表示101.11 ,2又7/8是10.111,1又7/16是1.0111
同样如果数字左移1位,就是*2 很明显这具有局限性,诸如1/3是0.01010101......,1/5是0.001100110011.....,1/10是0.000110011......
因此选择浮点,浮点主要通过移动二进制小数点来表示尽可能大的数值范围,兼顾精度和位数
IEEE于1985规范化了浮点数的表示方法
然后乘以2的E次幂
M通常是介于【1.0,2.0】的数,(-1)^s*M*2^E 就和10进制的 (-1)^s*M*10^E 一样,(-1)^s 控制正负,M 控制值,2^E 控制小数点左右移动几位。之后的frac是尾数,编码M但和M不同
单进度是32位,对应s1---exp8-----frac23 双精度的是s1------exp11-----frac52
规范化值指的是exp端不能全是0或者全是1,因为是特殊数
对于公式中的E,被解释为以偏置biased形式表示,所以E是exp-bias。
Exp的值,就是把exp的值一直作为一个正数,所以单精度7位数字的情况下,只需要看成7位的无符号整数, 是8位expon,并且是无符号数,但计算exp-bias是有符号数,
对于单精度,我有8个位,所以2^(8-1)-1=127,单精度的偏移值是127,同理双精度是1023
最小指数是00000....,最大是11111111...0
只需要采用无符号表达,比较各个位,把它当做无符号整数,我们可以通过使用这种偏移值表示法,来比较两个浮点数,就像无符号整数一样,我们可以将整个浮点数视为无符号整数并比较这两个数字 就可以得到真正的比较
所以指数使用这种偏置编码法,尾数采用隐含编码法,规格化表示的来源,所以我们总是要将 M规格化 我们总是将M规格化为 1.xxx……..X,我们相应地调整指数(来进行规格化)因此,如果我们想要表示的值是 100.01,我们将把它的二进制小数点左移,使之成为 1.00 然后我们调整指数来表示这种位移
那么,尾数域xXXX……X 中的位是,二进制点右边的所有数字,这个1一直隐藏的,我们甚至没有对它进行编码,我们只是扔掉它(不对这个1进行存储),所以这是一个小技巧,只是为了免费获得一位,好吧,尾数域的 xxx 位,二进制小数点之后的所有位在1.之后,所以最小的尾数域全是0 这相当于尾数是 1.0,所有位都是 1 的 frac 对应于 2—8,那是 1.111..
Exp的最小值是多少?不要把编码值和实际值混淆,是0,最大是2^8-1,是01111111,是255
那么E是范围是?我有偏置置,因此是-127<=E<=128。规范化值尾数总是有一个隐含的1,当想要表达0.0000多少的数,那个1限制了我们
因此非规格化的浮点数,exp全是0,且没有隐含的1,,所以M的值frac域编码值完全等价,所以数字是0.1111,而且E不是Exp-bias,而是1-bias。符号是隐含的前导0编码,不是1,因此exp是0,frac是0,那么就是0