目录
- 0 专栏介绍
- 1 非线性最小二乘法
- 2 基于非线性最小二乘的路径平滑
- 2.1 平滑性约束
- 2.2 曲率约束
- 2.3 障碍物约束
- 2.4 Ceres求解器求解
- 3 ROS C++仿真
0 专栏介绍
🔥课设、毕设、创新竞赛必备!🔥本专栏涉及更高阶的运动规划算法轨迹优化实战,包括:曲线生成、碰撞检测、安全走廊、优化建模(QP、SQP、NMPC、iLQR等)、轨迹优化(梯度法、曲线法等),每个算法都包含代码实现加深理解
🚀详情:运动规划实战进阶:轨迹优化篇
1 非线性最小二乘法
最小二乘问题表述如下
min x F ( x ) = 1 2 m min θ ∑ i = 1 m ∥ f i ( x ) ∥ 2 2 = 1 2 m min θ f T ( x ) f ( x ) \min _{\boldsymbol{x}}F\left( \boldsymbol{x} \right) =\frac{1}{2m}\min _{\boldsymbol{\theta }}\sum_{i=1}^m{\left\| f_i\left( \boldsymbol{x} \right) \right\| _{2}^{2}}=\frac{1}{2m}\min _{\boldsymbol{\theta }}\boldsymbol{f}^T\left( \boldsymbol{x} \right) \boldsymbol{f}\left( \boldsymbol{x} \right) xminF(x)=2m1θmini=1∑m∥fi(x)∥22=2m1θminfT(x)f(x)
其中 f ( x ) = [ f 1 ( x ) f 2 ( x ) ⋯ f m ( x ) ] T \boldsymbol{f}\left( \boldsymbol{x} \right) =\left[ \begin{matrix} f_1\left( \boldsymbol{x} \right)& f_2\left( \boldsymbol{x} \right)& \cdots& f_m\left( \boldsymbol{x} \right)\\\end{matrix} \right] ^T f(x)=[f1(x)f2(x)⋯fm(x)]T, f i ( ⋅ ) f_i\left( \cdot \right) fi(⋅)是关于第 i i i个观测样本的目标函数,当 f i ( ⋅ ) f_i\left( \cdot \right) fi(⋅)为线性函数时为线性最小二乘问题,否则是非线性最小二乘问题
非线性最小二乘在参数估计、图像处理、机器学习、机器人学、计算机视觉和计算几何等领域应用非常广泛
本文通过非线性最小二乘法的思想建模路径平滑问题,使当前路径与期望路径在各性能指标上的误差最小
2 基于非线性最小二乘的路径平滑
对路径序列 X = { x i = ( x i , y i ) } \mathcal{X} =\left\{ \boldsymbol{x}_i=\left( x_i,y_i \right) \right\} X={xi=(xi,yi)}设计以下代价函数,构造非线性最小二乘问题
f ( X ) = w s P s m o ( X ) + w κ P c u r ( X ) + w o P o b s ( X ) f\left( \mathcal{X} \right) =w_sP_{\mathrm{smo}}\left( \mathcal{X} \right) +w_{\kappa}P_{\mathrm{cur}}\left( \mathcal{X} \right) +w_oP_{\mathrm{obs}}\left( \mathcal{X} \right) f(X)=wsPsmo(X)+wκPcur(X)+woPobs(X)
2.1 平滑性约束
期望每段轨迹的长度近似相等,使整体运动更平坦,即
P s m o ( X ) = 1 2 ∑ i = 1 ∣ X ∣ − 2 ∥ Δ x i − Δ x i + 1 ∥ 2 2 P_{\mathrm{smo}}\left( \mathcal{X} \right) =\frac{1}{2}\sum_{i=1}^{\left| \mathcal{X} \right|-2}{\left\| \varDelta \boldsymbol{x}_i-\varDelta \boldsymbol{x}_{i+1} \right\| _{2}^{2}} Psmo(X)=21i=1∑∣X∣−2∥Δxi−Δxi+1∥22
代价函数编写如下:
template <typename T>
inline void addSmoothingResidual(const Eigen::Matrix<T, 2, 1>& pt_prev, const Eigen::Matrix<T, 2, 1>& pt,
const Eigen::Matrix<T, 2, 1>& pt_next, T& r) const
{
Eigen::Matrix<T, 2, 1> d_next = pt_next - pt;
Eigen::Matrix<T, 2, 1> d_prev = pt - pt_prev;
T next_to_prev_ratio = d_next.template block<2, 1>(0, 0).norm() / d_prev.template block<2, 1>(0, 0).norm();
Eigen::Matrix<T, 2, 1> d_diff = next_to_prev_ratio * d_next - d_prev;
r += (T)w_smooth_ * d_diff.dot(d_diff);
}
2.2 曲率约束
对每个节点轨迹的瞬时曲率进行了上界约束,即
P c u r ( X ) = 1 2 ∑ i = 1 ∣ X ∣ − 2 max { 0 , κ i − κ max } 2 P_{\mathrm{cur}}\left( \mathcal{X} \right) =\frac{1}{2}\sum_{i=1}^{\left| \mathcal{X} \right|-2}{\max \left\{ 0, \kappa _i-\kappa _{\max} \right\} ^2} Pcur(X)=21i=1∑∣X∣−2max{0,κi−κmax}2
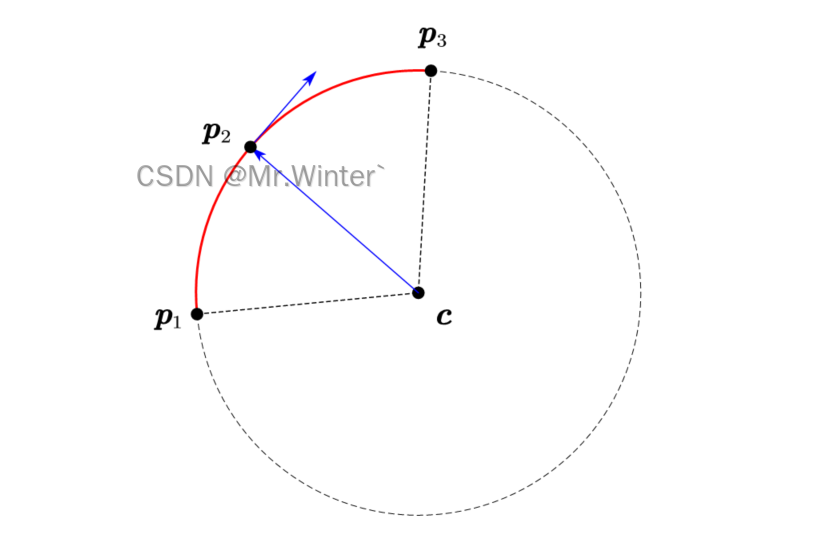
其中 κ i \kappa _i κi是由三个路径点 x i − 1 \boldsymbol{x}_{i-1} xi−1、 x i \boldsymbol{x}_i xi与 x i + 1 \boldsymbol{x}_{i+1} xi+1确定的圆的曲率,如下图所示
代价函数编写如下:
template <typename T>
inline void addCurvatureResidual(const Eigen::Matrix<T, 2, 1>& pt_prev, const Eigen::Matrix<T, 2, 1>& pt_curr,
const Eigen::Matrix<T, 2, 1>& pt_next, T& r) const
{
T turning_rad = calTurningRadius(pt_prev, pt_curr, pt_next);
T ki_minus_kmax = (T)1.0 / turning_rad - k_max_;
if (ki_minus_kmax <= (T)rmp::common::math::kMathEpsilon)
{
return;
}
r += (T)w_curvature_ * ki_minus_kmax * ki_minus_kmax; // objective function value
}
2.3 障碍物约束
惩罚机器人与障碍发生碰撞
P o b s ( X ) = 1 2 ∑ i ∈ I ( ∥ x i − o i ∥ 2 − d max ) 2 , I = { i ∣ ∥ x i − o i ∥ 2 < d max } P_{\mathrm{obs}}\left( \mathcal{X} \right) =\frac{1}{2}\sum_{i\in \mathcal{I}}^{}{\left( \left\| \boldsymbol{x}_i-\boldsymbol{o}_i \right\| _2-d_{\max} \right) ^2}, \mathcal{I} =\left\{ i|\left\| \boldsymbol{x}_i-\boldsymbol{o}_i \right\| _2<d_{\max} \right\} Pobs(X)=21i∈I∑(∥xi−oi∥2−dmax)2,I={i∣∥xi−oi∥2<dmax}
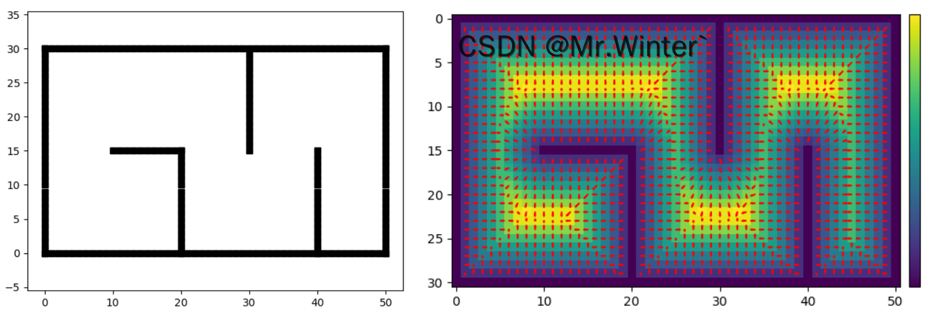
这里最小障碍距离 o i \boldsymbol{o}_i oi通过ESDF获取,可以参考相关文章:
代价函数编写如下:
template <typename T>
inline void addCostResidual(const Eigen::Matrix<T, 2, 1>& xi, T& r) const
{
T resolution = (T)costmap_->getResolution();
Eigen::Matrix<T, 2, 1> costmap_origin(costmap_->getOriginX(), costmap_->getOriginY());
Eigen::Matrix<T, 2, 1> interp_pos = (xi - costmap_origin.template cast<T>()) / resolution;
T value;
costmap_interpolator_->Evaluate((T)costmap_->getSizeInCellsY() - interp_pos[1] - (T)0.5, interp_pos[0] - (T)0.5,
&value);
T cost = value * resolution * resolution;
cost = cost > (T)(obs_dist_max_ * obs_dist_max_) ? (T)0 : cost;
r += (T)w_distance_ * cost; // esdf
}
2.4 Ceres求解器求解
Ceres是一个开源的 C++ 库,用于求解大规模非线性最小二乘问题。Ceres的设计强调高效性、灵活性和易用性,支持高效求解带有复杂约束的最优化问题,具有很强的扩展性。
对于Ceres而言,非线性最小二乘的形式泛化为
min x F ( x ) = 1 2 min x ∑ i ρ i ( ∥ f i ( x ) ∥ 2 2 ) s . t . l ≤ x ≤ u \min _{\boldsymbol{x}}F\left( \boldsymbol{x} \right) =\frac{1}{2}\min _{\boldsymbol{x }}\sum_{i}{\rho_i( \left\| f_i\left( \boldsymbol{x} \right) \right\| _{2}^{2})} \\ s.t.\ \ \ \ \boldsymbol{l} \le \boldsymbol{x} \le \boldsymbol{u} xminF(x)=21xmini∑ρi(∥fi(x)∥22)s.t. l≤x≤u
其中
ρ
i
(
∥
f
i
(
x
)
∥
2
2
)
\rho_i( \left\| f_i\left( \boldsymbol{x} \right) \right\| _{2}^{2})
ρi(∥fi(x)∥22)称为残差块(residual block),一个优化问题通常由多个残差块组成,每个残差块负责计算一个或多个残差;
f
i
(
⋅
)
f_i\left( \cdot \right)
fi(⋅)是代价函数,
ρ
i
(
⋅
)
\rho_i\left( \cdot \right)
ρi(⋅)是损失函数;
x
\boldsymbol{x}
x是优化变量或称为参数块(parameter blocks)。Ceres建模了上述有界非线性最小二乘问题,通过更新优化变量,使残差达到最小,此时的优化变量就是该问题的数值最优解
Ceres更详细的接口介绍和安装方法请参考数值优化 | 非线性最小二乘优化器Ceres安装教程与应用案例
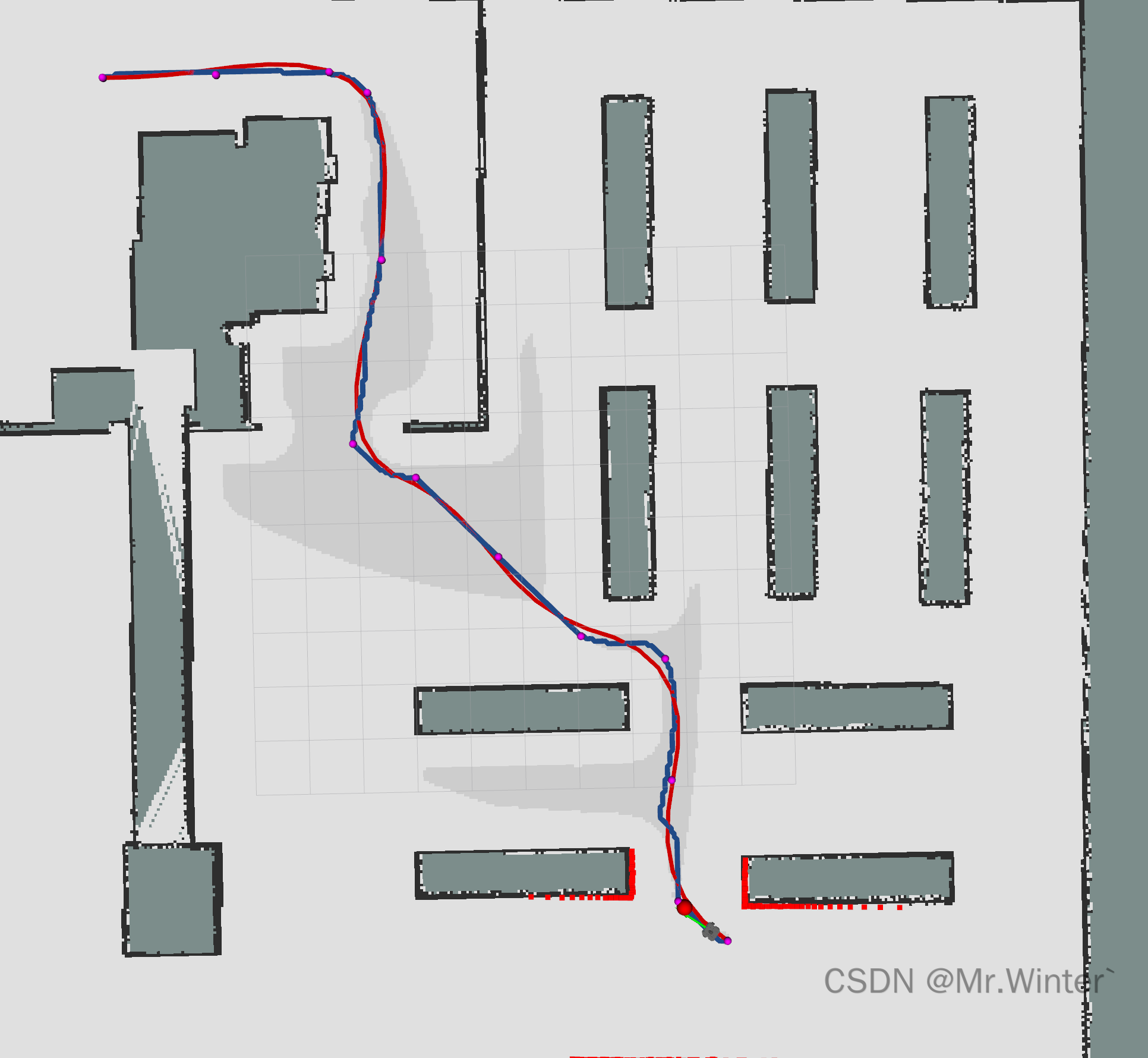
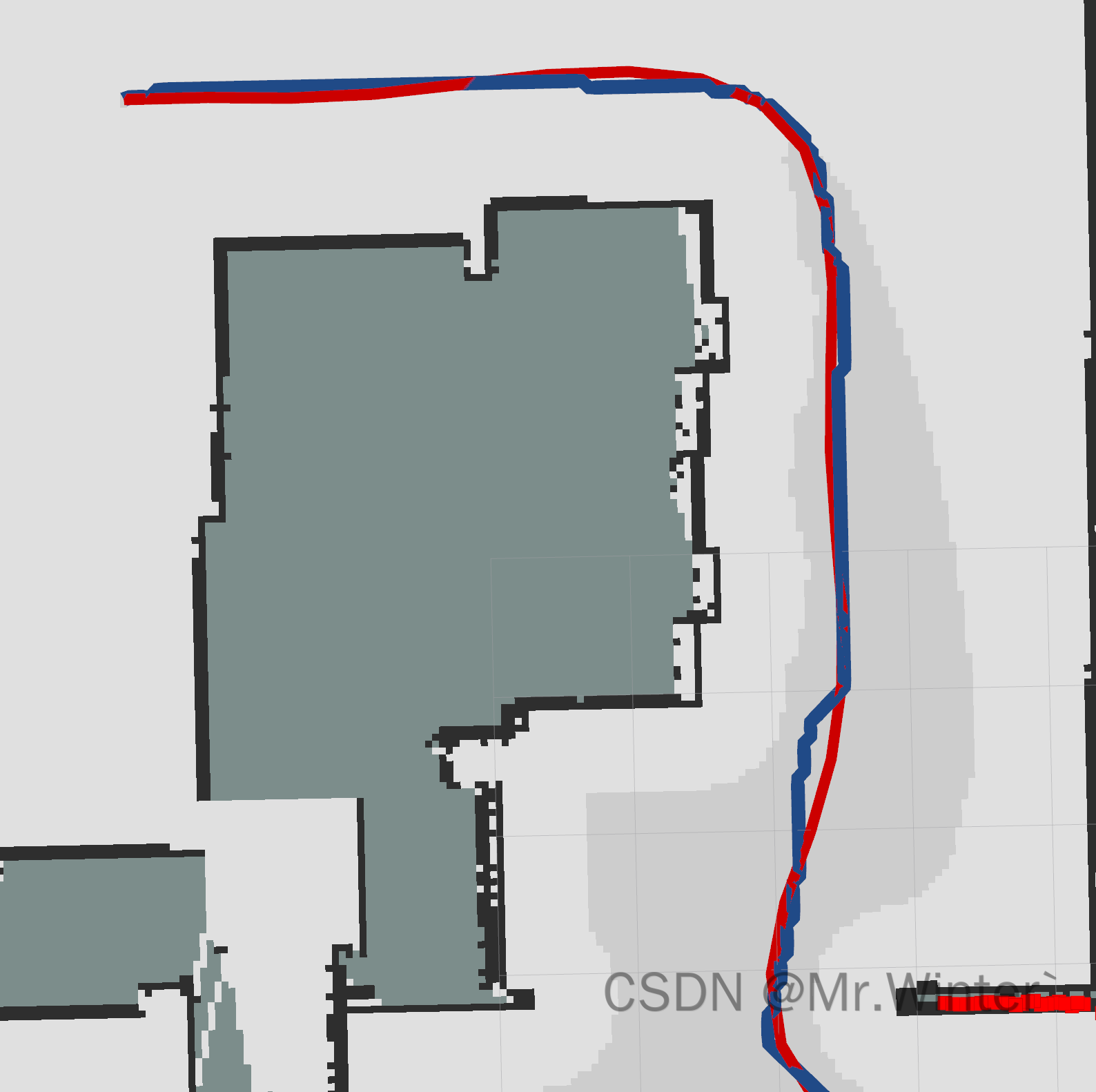
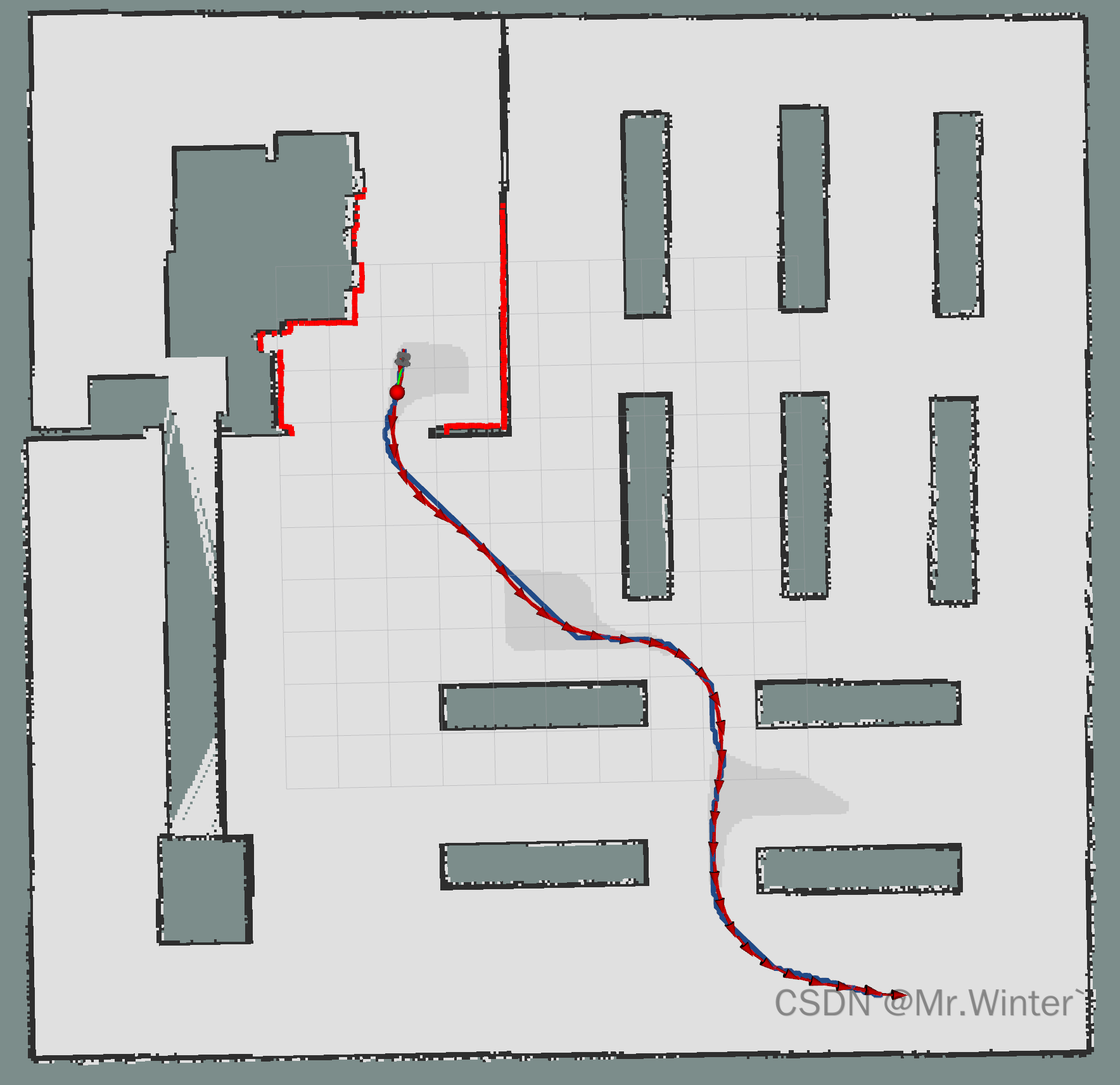
3 ROS C++仿真
核心代码如下所示
bool ConstrainedOptimizer::optimize(const Points3d& waypoints, ceres::Problem& problem)
{
// initialize trajectory to optimize
path_opt_.clear();
for (const auto& pt : waypoints)
{
path_opt_.emplace_back(pt.x(), pt.y(), pt.theta());
}
bool is_distance_layer_exist = false;
for (auto layer = costmap_ros_->getLayeredCostmap()->getPlugins()->begin();
layer != costmap_ros_->getLayeredCostmap()->getPlugins()->end(); ++layer)
{
distance_layer_ = boost::dynamic_pointer_cast<costmap_2d::DistanceLayer>(*layer);
if (distance_layer_)
{
is_distance_layer_exist = true;
break;
}
}
if (!is_distance_layer_exist)
{
R_ERROR << "Failed to get a Distance layer for potentional application.";
}
costmap_grid_ = std::make_shared<ceres::Grid2D<double>>(
distance_layer_->getEDFPtr(), 0, distance_layer_->getSizeInCellsY(), 0, distance_layer_->getSizeInCellsX());
auto costmap_interpolator = std::make_shared<ceres::BiCubicInterpolator<ceres::Grid2D<double>>>(*costmap_grid_);
// Create residual blocks
ceres::LossFunction* loss_function = NULL;
for (size_t i = 2; i < path_opt_.size(); i++)
{
Eigen::Vector3d origin_pose(waypoints[i - 1].x(), waypoints[i - 1].y(), waypoints[i - 1].theta());
OptimizerCostFunction* cost_function =
new OptimizerCostFunction(origin_pose, costmap_ros_->getCostmap(), costmap_interpolator, obs_dist_max_, k_max_,
w_obstacle_, w_smooth_, w_distance_, w_curvature_);
problem.AddResidualBlock(cost_function->AutoDiff(), loss_function, path_opt_[i - 2].data(), path_opt_[i - 1].data(),
path_opt_[i].data());
}
int poses_to_optimize = problem.NumParameterBlocks() - 4;
if (poses_to_optimize <= 0)
{
return false;
}
problem.SetParameterBlockConstant(path_opt_.front().data());
problem.SetParameterBlockConstant(path_opt_[1].data());
problem.SetParameterBlockConstant(path_opt_[path_opt_.size() - 2].data());
problem.SetParameterBlockConstant(path_opt_.back().data());
return true;
}
完整工程代码请联系下方博主名片获取
🔥 更多精彩专栏: