一、题目描述

原题传送门

给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。

请你 合并 nums2 到 nums1 中，使合并后的数组同样按 非递减顺序 排列。

注意：最终，合并后数组不应由函数返回，而是存储在数组 nums1 中。为了应对这种情况，nums1 的初始长度为 m + n，其中前 m 个元素表示应合并的元素，后 n 个元素为 0 ，应忽略。nums2 的长度为 n 。

示例 1：

输入：nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出：[1,2,2,3,5,6]
解释：需要合并 [1,2,3] 和 [2,5,6] 。
合并结果是 [1,2,2,3,5,6] ，其中斜体加粗标注的为 nums1 中的元素。

示例 2：

输入：nums1 = [1], m = 1, nums2 = [], n = 0
输出：[1]
解释：需要合并 [1] 和 [] 。
合并结果是 [1] 。

示例 3：

输入：nums1 = [0], m = 0, nums2 = [1], n = 1
输出：[1]
解释：需要合并的数组是 [] 和 [1] 。
合并结果是 [1] 。
注意，因为 m = 0 ，所以 nums1 中没有元素。nums1 中仅存的 0 仅仅是为了确保合并结果可以顺利存放到 nums1 中。

void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n)

• 有很重要的一点在这里就给大家分析清楚，就是题目的主函数接口给到的形参，这个m是原本nums1数组中元素的个数，n是原本nums2数组中元素的个数，那有同学问这个nums1Size和nums2Size是干嘛用的
• 题目中很明确地有写出，两个合并后的数组并不是存放在另一个数组中，而是存放在nums1中，但是nums1的容量有限，所以在题目的初始，就这个nums1的长度扩充为【m + n】，这样刚好可以放得过

二、思路分析

好，看完题目的描述，我们来分析一下如何去求解这道题目

• 首先题目的意思是将两个有序的数组合并成一个数组，而且这个数组也是要有序的
• 有关这道题的解题思路其实就是归并排序的算法思维，可以去看一下我的这篇文章排序算法——归并排序，里面详细介绍了如何使用归并的一个思维对一个无序的数组进行排序。
• 我们本题其实也是一样，需要三个指针，两个指针分别指向nums1和nums2的末尾位置。那为什么要指向末尾位置呢❓，不指向开头位置，从下图我们可以看出，若是这个让两个指针分别指向两个数组的首部，看这个时候2 < 6，此时2就会被赋值到6的位置，那这个时候因为没有提前去保存这个6，所以就导致这个6丢失了，你少了一个元素这其实已经违背了题目的本质
• 刚才说到赋值，那要怎么赋值呢，我们这里定义一个指针j，让其指向对nums1扩容之后的数组个数 - 1的位置，也就是nums1数组的最后一个位置

三、整体代码展示

整体代码如下，先给到大家，然后再一一做分析

void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n){
    int i1 = m - 1, i2 = n - 1, j = nums1Size - 1;
    while(i1 >=0 && i2 >= 0)
    {       //只要有< 0 便结束循环
        if(nums1[i1] > nums2[i2])
        {
            nums1[j--] = nums1[i1--];
        }
        else
        {
            nums1[j--] = nums2[i2--];
        }
    }

    //如果是i1 > 0了，则无需做变化
    //若是是i2 > 0了，则需要将nums2中的剩余元素拷贝过来
    while(i2 >= 0)
    {
        nums1[j--] = nums2[i2--];
    }
}

四、代码详解【步步算法图解】

然后我们通过这段代码来给大家分析一下

• 从上述总体代码可以看出，整体有一个遍历的逻辑，谁大了就从nums1后面赋值进去，但是可以看到最后还有一段逻辑，这其实就是考虑的一种特殊情况，我们下面从两种情况分别来讲讲

情况一：nums2遍历完，nums1无需动

首先的话就是这种正常的情况，也就是nums2遍历完了之后，nums1中还有元素剩余，其实这个时候剩余的元素已经是呈现一个递增的排序，而且一定是比后面比较完的元素要来得大的，因此无需移动

我们还是通过算法图解来具体看看这种正常情况

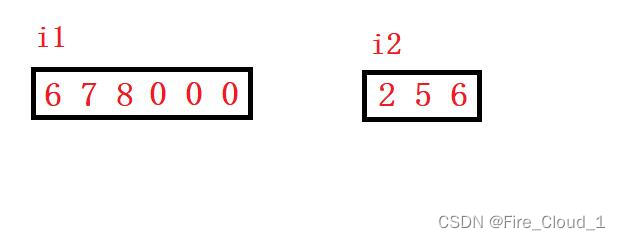
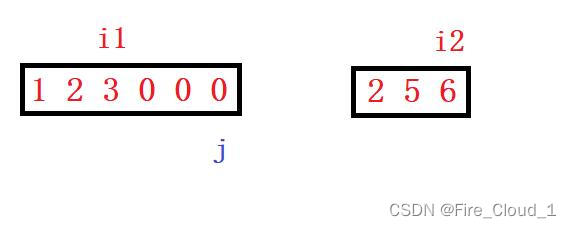
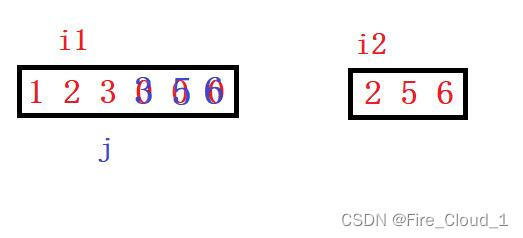
• 首先让i1指向nums1的最后一个元素，让i2指向nums2的最后一个元素，j则是指向nums1数组扩容之后的最后一个位置。

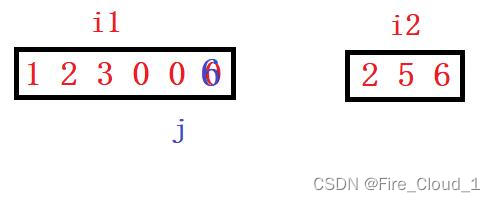
• 此时开始比较3 < 6，因此将j的位置放上6，在赋值完之后指针i2前移一个位置，并且将指针j也前移一个位置

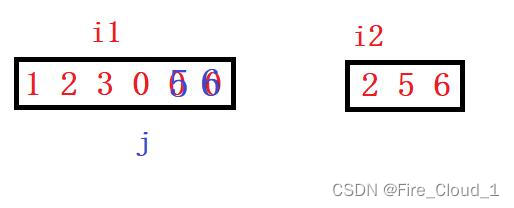
• 然后又开始比较，3 < 5，因此将5赋值过去，然后i2–，j–

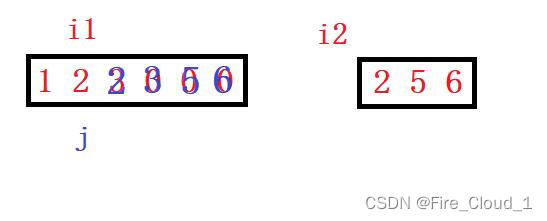
• 此时3 > 2，所以将3赋值过去i1–，j–

• 此时可以看到2 == 2，无论放哪个过去都可以，我们选择i2位置上的2，然后i2–，j–
• 然后这个时候【i2 < 0】，因此退出外层的while循环，但是可以看到，nums1还有2个元素没有进行比较赋值，但是从图中可以看出，已经是呈现出一个有序的场景，这个是我在标题中说的nums2遍历完，nums1无需动

但是除了这种情况，还有一种情况就是当nums1遍历完了，但是nums2还没有遍历完，有剩余的元素，因此就要做另外的操作，我们一起来看看

情况二：nums1遍历完，nums2还有剩余元素【特殊】

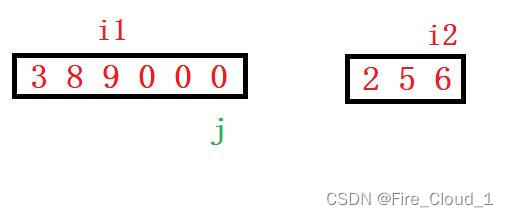
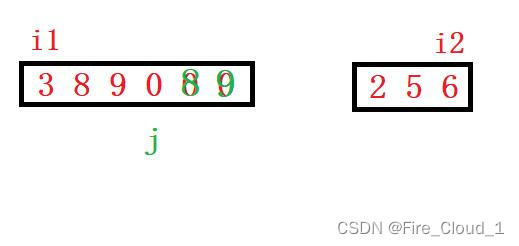
• 我们以下面这种情况为例，来做一个演示

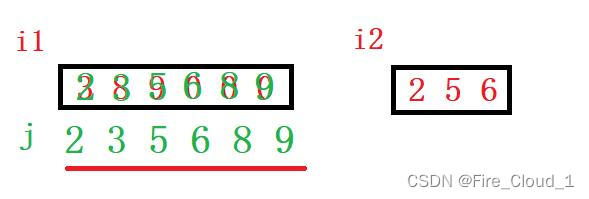
• 然后开始比较9 > 6，把9赋值过去，i1–，j–

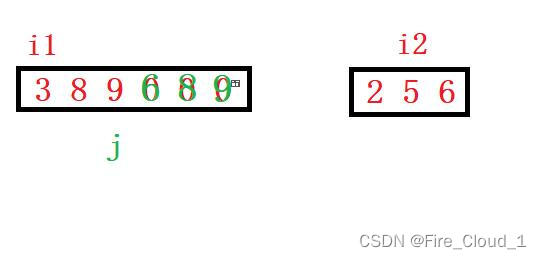
• 比较8 > 6，把8赋值过去，i1–，j–

• 比较6 > 3，把6赋值过去，i2–，j–

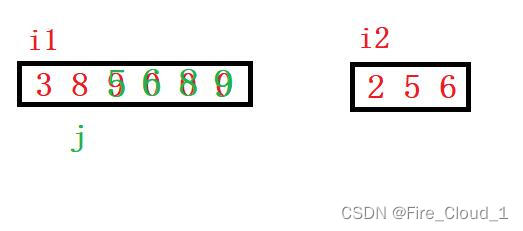
• 比较5 > 3，把5赋值过去，i2–，j–

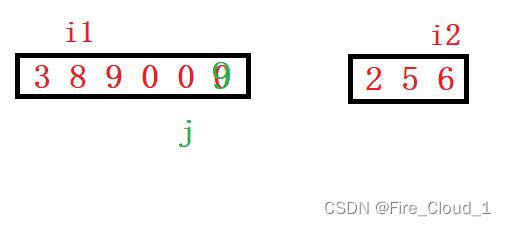
• 比较3 > 2，把3赋值过去，i1–，j–
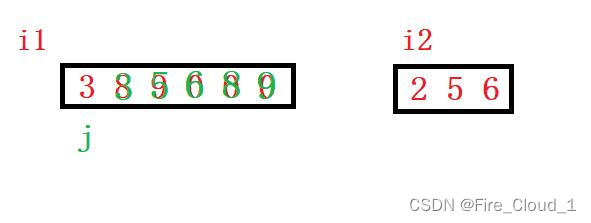
• 此时可以看到，遍历nums1的指针i1< 0，因此退出while循环，但是可以看到，nums2中还有一个2没有被赋值过去，但此时循环已经结束了，怎么办呢？
• 这个时候我们再单独为nums2做一个继续的遍历，然后直接减剩余元素放过来即可，因为一定是比后面元素小而且有序的，用到的就是下面这段循环

while(i2 >= 0)
{
    nums1[j--] = nums2[i2--];
}

• 最后的结果就是这样，无需返回，主函数返回类型是void，只是做一个改动即可
  

五、总结与提炼

• 最后我们来总结一下本文所介绍的内容，本文讲解来一道力扣中有关合并两个数组元素的内容，这个思维其实是基于归并排序的，只是对于本题，需要新数组的内容直接放到num1中，因此做了一些改动，需要让两个数组从后往前进行一个遍历，然后一一赋值
• 但是对于这种比较，也具有两种情况，我们也做了分类讨论，一种就是nums2遍历完了，但是nums1没有遍历完，此时无需移动元素，保持元素的数据就行；另外一种就是nums1遍历完了，但是nums2没有遍历完，这个时候就需要再对nums2的剩余元素继续拿过来就可以

以上就是本文所要描述的所有内容，感谢您对本文的观看，如有疑问请于评论区留言或者私信我都可以🍀