上次更新
[2017.12.21]AT CDQZ 十二月中旬联训。
前言
刚刚写完了一篇关于KMP的一篇博客,在那里我就说,强烈建议同学们“进修”一下“AC自动机”。而现在我又要说:如果你对KMP算法还没有一个深入的理解,先不要急着学“AC自动机”,因为它的思想是完全基于KMP算法上的。所以给各位同学一个友情链接,看完它再进行AC自动机的学习。
友情链接1:神奇的KMP——线性时间匹配算法(初学者请进)
友情链接2:Trie 前缀树/字典树/单词查找树(数据结构)
(小时候一直天真地觉得:“哇!竟然有这么强的一种数据结构,竟然能自动AC。”后来才知道“AC自动机”其实是“Aho-Corasick自动机”的简称。并不是说用了就可以“AC”的意思。)
1.AC自动机的实现功能与原理
在360百科中对AC自动机的用途以及原理给出了这样的解释:
(AC自动机的)一个常见的例子就是给出n个单词,再给出一段包含m个字符的文章,让你找出有多少个单词在文章里出现过。
要搞懂AC自动机,先得有模式树(字典树)Trie和KMP模式匹配算法的基础知识。 AC自动机算法分为3步:构造一棵Trie树,构造失败指针和模式匹配过程。
如果你对KMP算法了解的话,应该知道KMP算法中的next函数(shift函数或者fail函数)是干什么用的。KMP中我们用两个指针i和j分别表示,A[i-j+ 1..i]与B[1..j]完全相等。也就是说,i是不断增加的,随着i的增加j相应地变化,且j满足以A[i]结尾的长度为j的字符串正好匹配B串的前 j个字符,当A[i+1]≠B[j+1],KMP的策略是调整j的位置(减小j值)使得A[i-j+1..i]与B[1..j]保持匹配且新的B[j+1]恰好与A[i+1]匹配,而next函数恰恰记录了这个j应该调整到的位置。同样AC自动机的失败指针具有同样的功能,也就是说当我们的模式串在Trie上进行匹配时,如果与当前节点的关键字不能继续匹配,就应该去当前节点的失败指针所指向的节点继续进行匹配。
请忽略掉上文中没有加粗的内容。
(一是因为它说得太笼统,而是因为它对变量的定义与使用与我的是不一样的,容易误导读者。)
KMP算法只能用于单个模式串的字符串匹配(我们在字符串T中寻找字符串P的出现位置,T叫做文本串,P叫做模式串),如果我要是想在同一个文本串中给n个模式串进行匹配,那我就得跑n遍KMP,这样做是非常浪费时间的(尽管KMP是线性时间算法)。我们能不能找到一种方法,只在文本串中走一遍就能对所有模式串进行匹配呢?这就是AC自动机。
2.AC自动机与Tire树和KMP之间的关系
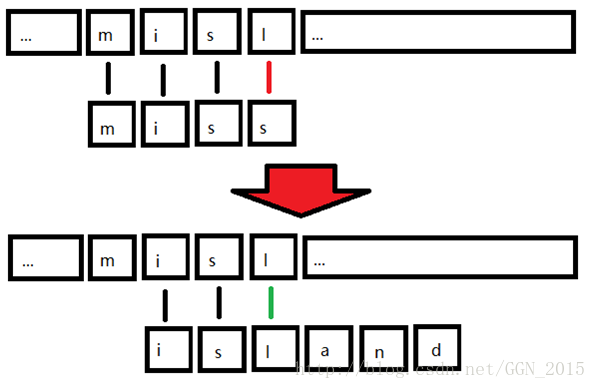
AC自动机的原理与KMP是完全相同的,就是当我出现了一次“失配”后并不是从整个模式串的开头重新匹配,而是找到一个位置,把它变为“当前节点”继续匹配。就比如说我在一个T=”…misl…”(“…”表示省略部分)的文本串中匹配模式串P[0]=”miss”和P[1]=”island”。我先匹配出“mis”然后失配,如果这是我们能把它用“失配边”(用来描述一个结点失配之后的状态转移)实现,把它转移到“island”的配对,那真是极好的!
(非常不好理解的地方来了:)
也就是说对于Trie中的每一个结点所表示的一个模式串前缀我们都要找到它最长的(不为它本身的)一个后缀,满足是整个Trie的一个前缀。然后这个整个Trie的一个前缀的末尾结点就是当前失配边所指向的结点。这可以用BFS的方法遍历这棵树,递推求得。最后的得到带有“失配边”的一个Trie树(我叫它“AC-Trie”)。
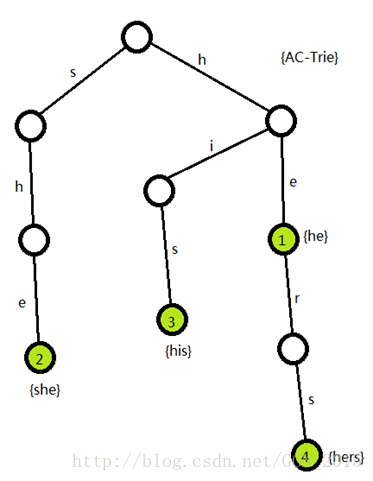
比如说,原来的Trie树是这样的(圈中数字代表权值,空白代表为0):
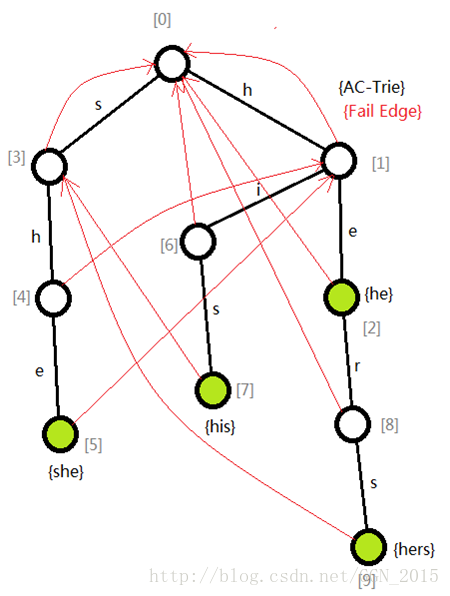
处理之后就会变成这样(中括号中的数字代表结点的编号):
另外,AC自动机的结果输出功能是不同于KMP的。就比如说如果P[i]=”his”得到了成功匹配,其实这个时候
P[j]=”is”也得到了成功匹配(因为P[j]是P[i]的后缀)。所以,我们在输出结果的那时候一定要考虑到这种情况。
分析这样一个问题:P[j]的成功匹配输出与f[J]的失配函数是否有着某种联系。f[j]表示的是线段树中最长的一个前缀为P[j]的一个后缀,如果f[j]恰好为我的一个模式串,这时候f[j]也需要输出。如果f[f[j]]恰为一个模式串,而f[f[j]]是f[j]串的一个后缀,如果f[j]满足那么f[f[j]]自然也需要输出。我们可以用一个叫last的数组储存,如果一个模式串成功地匹配,那么他的最长的 满足为整个trie树的一个前缀的 一个后缀的结点号。在正规的文献中这个“last”数组被称为“后缀链接”(suffix link)。
3.AC自动机的实现
有了之前的这些理论,我们可以尝试着编写一下它的源代码(讲解我都写到代码注释里面去了)。
关于Trie树部分的注释参见友情链接:
样例代码:
int idx(char c) //用于返回一个字符的索引值
{
return c-'a';
}
struct AC_Trie
{
int next[MaxNode][26];//所有子结点
int val[MaxNode];//结点的权值
int size;//结点总数
AC_Trie()//构造函数
{
size=0;
memset(next[0],0,sizeof(next[0]));
}
void insert(char* str,int Value)//插入一个字符串
{//详见Trie树解析
int nodeNow=0,n=strlen(str);
for(int i=0;i<n;i++)
{
int charNow=idx(str[i]);
if(next[nodeNow][charNow]==0)
{
next[nodeNow][charNow]=++size;
memset(next[size],0,sizeof(next[size]));
val[size]=0;
}
nodeNow=next[nodeNow][charNow];
}
val[nodeNow]=Value;
}
int Search(char* str)//查询一个字符串是否出现过
{//同上,详见Trie树解析
int nodeNow=0,n=strlen(str);
for(int i=0;i<n;i++)
{
int charNow=idx(str[i]);
if(next[nodeNow][charNow]==0)
return 0;
nodeNow=next[nodeNow][charNow];
}
return val[nodeNow];
}
int f[MaxNode];//失配函数
int last[MaxNode];
//last[i]表示如果结点j所代表的的模式串满足匹配
//那么last[i]所表示的模式串也需要输出
void print(int j)
{
if(j!=0)
{
printf("%d:%d\n",j,val[j]);
print(last[j]);//递归输出last[j]
}
}//该print函数并不是很完备,完备的请同学们自己脑补一下吧
int getFail()//BFS计算失配边
{
queue<int>q;
f[0]=0;//规定f[0]=0;
for(int c=0;c<26;c++)//因为与0号结点相邻的结点前面只有0号结点一个结点
{//所以f[零号结点的儿子]=0
int nodeNow=next[0][c];
if(nodeNow!=0)//如果这个儿子存在,接把他的失配边赋成0
{
f[nodeNow]=0;
q.push(nodeNow);//顺道把这个儿子结点放入BFS队列中
last[nodeNow]=0;
}
}
while(q.empty()!=0)//BFS队列非空
{
int r=q.front();q.pop();//BFS队列中弹出一个结点
for(int c=0;c<26;c++)//对于这个节点的所有儿子
{
int nodeNow=next[r][c];
if(nodeNow==0)
continue;
q.push(nodeNow);//当前结点入队入队
int v=f[r];
while(v!=0 && next[v][c]==0)
v=f[v];//一直在失配边上跑,直到找到一个以'c'代表的字符为结尾的一个Trie的前缀
f[nodeNow]=next[v][c];//当前结点的失配边就连同到它身上
last[nodeNow]=val[f[nodeNow]]?f[nodeNow]:last[f[nodeNow]];
//如果失配边连着的位置恰好是一个模式串的结尾,那么他的last就是他的f
//否则他的last就是“他的f的f”
}
}
}
};
4.后记
写完AC自动机这篇之后,我还想学一学关于后缀数组的一些东西。
(温馨提示:我的代码是现写的,图片是现画的,所以不建议直接复制,可能会存在无数的漏洞。)
友情链接:Goseqh同学的AC自动机详解
他的代码比较完备,有需要的同学可以去看一看。
希望这篇文章能够加对各位同学有所帮助。赶稿匆忙,如有谬误,望各位同学谅解。
[2017.12.21]终于自己写出了AC自动机,开心,但是还没评测..
[2017.12.22]此代码有严重bug,请不要使用!
#include<cstdio>
#include<queue>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=1000000+10;
struct ACAM{
int nxt[maxn][27],val[maxn],fail[maxn],last[maxn],cnt[170];
int ncnt;
void init(){
ncnt=0;//start node is 0
memset(cnt,0,sizeof(cnt));
}
ACAM(){init();}
void addstr(const char* s,int v){
int now=0;//start node
for(int i=0;s[i];i++){
int idx=s[i]-'a'+1;
if(nxt[now][idx]==0){
nxt[now][idx]=++ncnt;//new node
memset(nxt[ncnt],0,sizeof(nxt[ncnt]));
val[ncnt]=0;
}
now=nxt[now][idx];
}
val[now]=v;//set value
}
void print(int u){
if(u!=0){
print(last[u]);
//printf(" %3d. ",val[u]);
cnt[val[u]]++;
}
}
void getFail(){
//printf("\n getFail. \n\n");
queue<int>Q;
for(int i=1;i<=25;i++){
int u=nxt[0][i];
if(u!=0){
fail[u]=0;
Q.push(u);
}
}
//printf("\n step 2. \n\n");
while(!Q.empty()){
int x=Q.front();Q.pop();
//printf("\n x = %d. \n\n",x);
for(int i=1;i<=25;i++){
int u=nxt[x][i];
//printf("\n u = %d. \n\n",u);
if(u!=0){
int j=fail[x];
while(j!=0 && nxt[j][i]==0)
j=fail[j];
fail[u]=nxt[j][i];
last[u]=val[fail[u]]?fail[u]:last[fail[u]];
Q.push(u);
}
}
}
}
void match(const char* s){
int now=0;
for(int i=0;s[i];i++){
//printf(" i = %d. \n",i);
int idx=s[i]-'a'+1;
while(now!=0 && nxt[now][idx]==0)
now=fail[now];
now=nxt[now][idx];
if(val[now]){
/*printf("find at %6d. : ",i);*/print(now);
//putchar('\n');
}else if(last[now]){
/*printf("find at %6d. : ",i);*/print(last[now]);
//putchar('\n');
}
}
}
}acam;
char s[maxn],tmp[maxn];
int debug_main(){
for(;;){
int op;scanf("%d",&op);
if(op==1){
scanf("%s",tmp);scanf("%d",&op);
if(op==0){
printf("\n error = \"value leq 0\". \n\n");
system("pause>nul");
}else{
acam.addstr(tmp,op);
printf("\n OK. \n\n");
}
}else if(op==2){
acam.getFail();
printf("\n OK. \n\n");
}else if(op==3){
scanf("%s",s);
acam.match(s);
printf("\n ans = \"solve end\". \n\n");
}else{
printf("\n error = \"unknown instruction\". \n\n");
system("pause>nul");
}
}
return 0;
}
char tp[150+2][80];
int main(){
int N;
while(scanf("%d",&N) && N){
acam.init();
for(int i=1;i<=N;i++){
scanf("%s",tp[i]);
acam.addstr(tp[i],i);
}
acam.getFail();
scanf("%s",s);
acam.match(s);
int ans=0;
for(int i=1;i<=N;i++){
ans=max(ans,acam.cnt[i]);
}
printf("%d\n",ans);
for(int i=1;i<=N;i++){
if(acam.cnt[i]==ans){
printf("%s\n",tp[i]);
}
}
}
return 0;
}