还是说,自己实现一遍比较好。隐马模型用输入法的例子记住它。
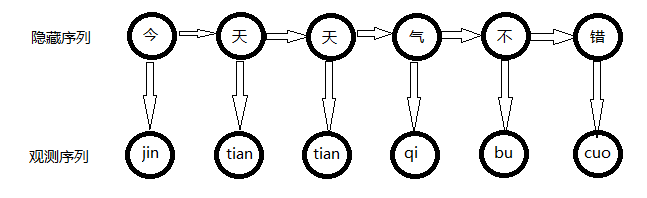
隐藏序列是汉字,观测序列是拼音,这个最浅显没有错。由观察序列求最优的隐藏序列。
它是有三个主要问题的,这个问题最好用色子举例。
初始概率矩阵:找出所有出现在词首的汉字,并统计它们出现在词首的次数,这个汉字的初始概率就是以这个汉字开始的单词/所有单词(是词库所有词还是语料所有词(重复的问题,为什么 )),没统计的汉字就认为出现在词首的概率是0,不写入数据库。
发射概率矩阵:汉字转移到下一个汉字的概率,找出字典中每个汉字后面出现的汉字集合,并统计概率。
转移概率矩阵:
大致思路呢就是根据拼音,找出它的汉字list,然后根据list找出一条最佳路径。
怎么找呢?用马尔可夫概率找啊,概率是什么?用色子来模拟啊,色子模型是点数预测动过手脚的色子序列,色子掷出每一个点的概率是不同的,一开始呢,是能掷出这个点数的色子序列,掷不出来的色子概率为0就不要了,初始概率就是它们掷出的概率,那么这样的话,每次取最大概率不就完事了吗?的确是这样,因为它们的转移概率是相同的,这种情况就是每次找最大概率就行,根本不用计算,这是最简单的模型。
再深一步,如果说,总喜欢透大一点的呢?就是有偏好,例如投完三面色子,喜欢投比它大的,四面色子和六面大一些,投完四面色子投六面筛子大一些,这样肉眼就看不出来了,跟以前有关系,这就是转移概率。
然后就是输出概率,实际上,对于正常色子来说,你是能直接预测出来,但是动过手脚的色子,转移概率一样的情况下,你也是能预测出来的,选概率最大的嘛,只不过你需要按照它的概率表来算了是吧。但两个字之间是没有关系的,一眼看出来也是一样的。
如果转移概率+输出概率结合到一起,就不一样了,这时候,哪一个概率是最大的,是由前面的决定的,而不仅仅是输出概率,这样一条路都是最大的,那么还要什么反向算法呢?那么起始概率呢?
维特比算法,算的是最短路径,
维特比就是这么算最短路径的,这关于输入法有什么关系呢?
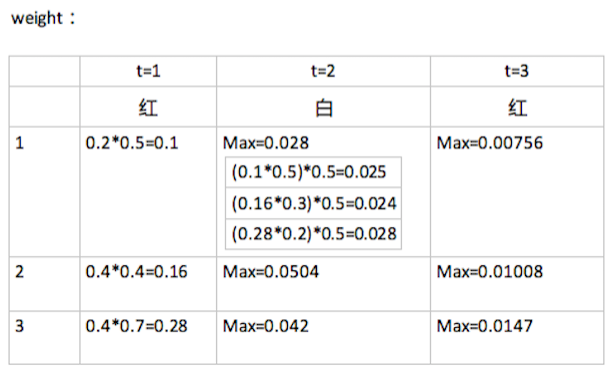
的确没什么关系,但是不全部算出来,你是不知道最大值,可以算最大值,那么在这里,也可以是节点的最大值。那么反向算法是怎么回事呢?因为中间不再是最大值!看下图:
(1)在t=2时刻,因为i_3 = 3,状态3的最大概率来源于状态3(上图没有显示出来,但可以参考状态1的计算过程)
(2)在t=1时刻,因为i_2 = 3,也可以得到最大概率来源于状态3
最后得到最优路径为(3,3,3)
这么说来,后向算法也是有必要的了。保留一个根。
对于起始概率来说,投色子并没有起始概率的观念,起始概率就是最大的那个概率啊,起始概率是一个节点概率,转移概率是线上概率,那么输出概率呢?合理的解释是以词语,短语表达式为语料,初始概率就是出现在头部的概率,转移概率就是这个字转向后面字的概率(怎么算呢?),统计的过程就是找出字典中每个汉字后面出现的汉字集合,并统计概率。<char, <char, count>>,然后再算成概率 <char, <char, p>>,发射概率呢?用<拼音,<字,计数>>,然后转换成概率<拼音,<字,概率>>,算法呢,就是以初始概率为开始,然后后面乘上转移概率,到节点处还要乘上发射概率,这样乘到最后,就是最佳匹配句子,为什么呢?因为这样乘出来的值,一定就是当前最佳概率组合,而当前最佳概率组合,不一定是过去最佳概率组合产生的,毕竟有那两个概率在,转移概率代表本概率受前面概率影响,发射概率代表本概率受当下概率影响。
色子掷出的序列是观察序列,用什么色子掷出来的是隐藏序列,拼音是观察序列,汉字是隐藏序列
一开始是什么色子是初始概率,
那么就做好了,注意语料不要太长。
马尔可夫模型都接触这么长时间了,原理肯定没错了。
n-best:此时,在每个结点不是只保留最小值,而是保留top N的最值。计算复杂度会增加n倍。每个节点保留最短路径的一个列表和这条第n短的前一个节点是什么,这样到最后取第n小,每次回溯节点也是第n小。这就是全局第二优?
每日一个知识点:
马尔可夫解决的三个问题:
1)知道骰子有几种(隐含状态数量),每种骰子是什么(转换概率),根据掷骰子掷出的结果(可见状态链),我想知道每次掷出来的都是哪种骰子(隐含状态链)。
2)还是知道骰子有几种(隐含状态数量),每种骰子是什么(转换概率),根据掷骰子掷出的结果(可见状态链),我想知道掷出这个结果的概率。
3)知道骰子有几种(隐含状态数量),不知道每种骰子是什么(转换概率),观测到很多次掷骰子的结果(可见状态链),我想反推出每种骰子是什么(转换概率)。
一般我们讨论第一种问题。上述问题的描述是有问题的,不知道每种筛子是什么并不是转换概率。