控制算法简析5——被控系统分析

承接上一篇(控制算法简析4——物理世界与控制工程)。
一旦获得了系统的状态空间或传递函数形式的数学模型，我们便可以分析这些模型来预测系统在时域和频域中的动态响应。通常将控制系统设计为高稳定性，高响应速度，低稳态误差，以及减小振荡。也就是“稳准快”。在本节中，我们将展示如何从系统模型中确定这些动态属性。

时域响应概述

时域响应表示动态系统的状态在受到特定输入时随时间的变化。由于我们得出的模型由微分方程组成，因此必须执行一些积分以确定系统的时域响应，对于某些简单的系统，可以使用闭区间的形式分析解决。但是，对于大多数系统，尤其是非线性系统或需要复杂输入的系统，此积分必须以数字方式进行，幸运的是，MATLAB提供了许多有用的资源来计算多种类型的输入来获得时域响应。
线性动态系统的时域响应由瞬态响应和稳态响应组成，瞬态响应取决于初始条件，稳态响应取决于系统输入，这些分别对应于齐次微分方程的特定解。

频域响应概述

本教程中介绍的所有示例均通过线性常数系数微分方程建模，因此均为线性不变(LTI)。LTI系统具有极其重要的特性，如果系统的输入为正弦波，则稳态输出也将是相同频率的正弦波，但通常具有不同的幅度和相位。这些幅度和相位差表示为频率的函数，即组成了系统的频率响应。
LTI备注：
在这里插入图片描述请添加图片描述

可以通过以下方式从系统的传递函数中找到系统的频域响应：创建频率向量(从0到无穷大之间变化)，并计算在这些频率下的传递函数的值。如果 $G (s)$ 是系统的开环传递函数，而 $\omega$ 是频率矢量，则可以绘制 $G (j w)$ 与 $\omega$ 的关系图。由于 $G (j w)$ 是复数，因此我们可以绘制其幅值和相位(伯德图)，也可以绘制其在复平面上的位置(奈奎施特图)，两种方法显示相同的信息，但方式不同。

稳定性

出于我们的目的，我们将使用“有界输入有界输出(BIBO)的稳定性定义，该定义指出如果输出对所有输入保持有界，则系统是稳定的。实际上，这意味着系统在运行时不会“发散”。
传递函数表示法在分析系统稳定性时特别有用，如果传递函数的所有极点(分母等于0的 $s$ 的值)都为负实部，则系统是稳定的。如果任一极点具有正实部，则系统不稳定。如果我们查看复数 $s$ 平面上的极点，则所有极点都必须在左半平面(LHP)中来确保稳定性。如果在虚轴上有任何一对对偶极点，则系统在一定程度上是稳定的，并且系统将趋于振荡，具有纯虚数极点的系统不被认为是BIBO稳定的，对于这样的系统，将存在无界响应的有界输入。LTI系统模型的极点可以使用“pole”命令，其示例如下所示：

s = tf('s');
G = 1/(s^2+2*s+5)
pole(G)	% 计算传递函数的极点

在这里插入图片描述

可以看出极点的实部均为负值，因此系统是稳定的。

系统的阶

动态系统的阶是其微分方程的最高导数的阶，同样，它是传递函数分母中 $s$ 的最高次幂。一、二阶和高阶系统的重要特性将在下面进行回顾。

一阶系统

一阶系统是最简单的动态系统，一些常见的示例包括质量块阻尼系统和RC电路。
一阶微分方程的一般形式如下：

$y^{'} + a y = b u$

一阶传递函数的形式是：

$G(s)=\frac{b}{s+a}=\frac{k_{dc}}{\tau s+1}$

其中参数 $k_{dc}$ 和 $\tau$ 表征了一阶系统的特征。

零极点：一阶系统只有一个极点，在这种情况下 $s = - a$ ，因此，如果 $a$ 为正，则系统稳定；如果 $a$ 为负，则系统不稳定，标准一阶系统没有零点。
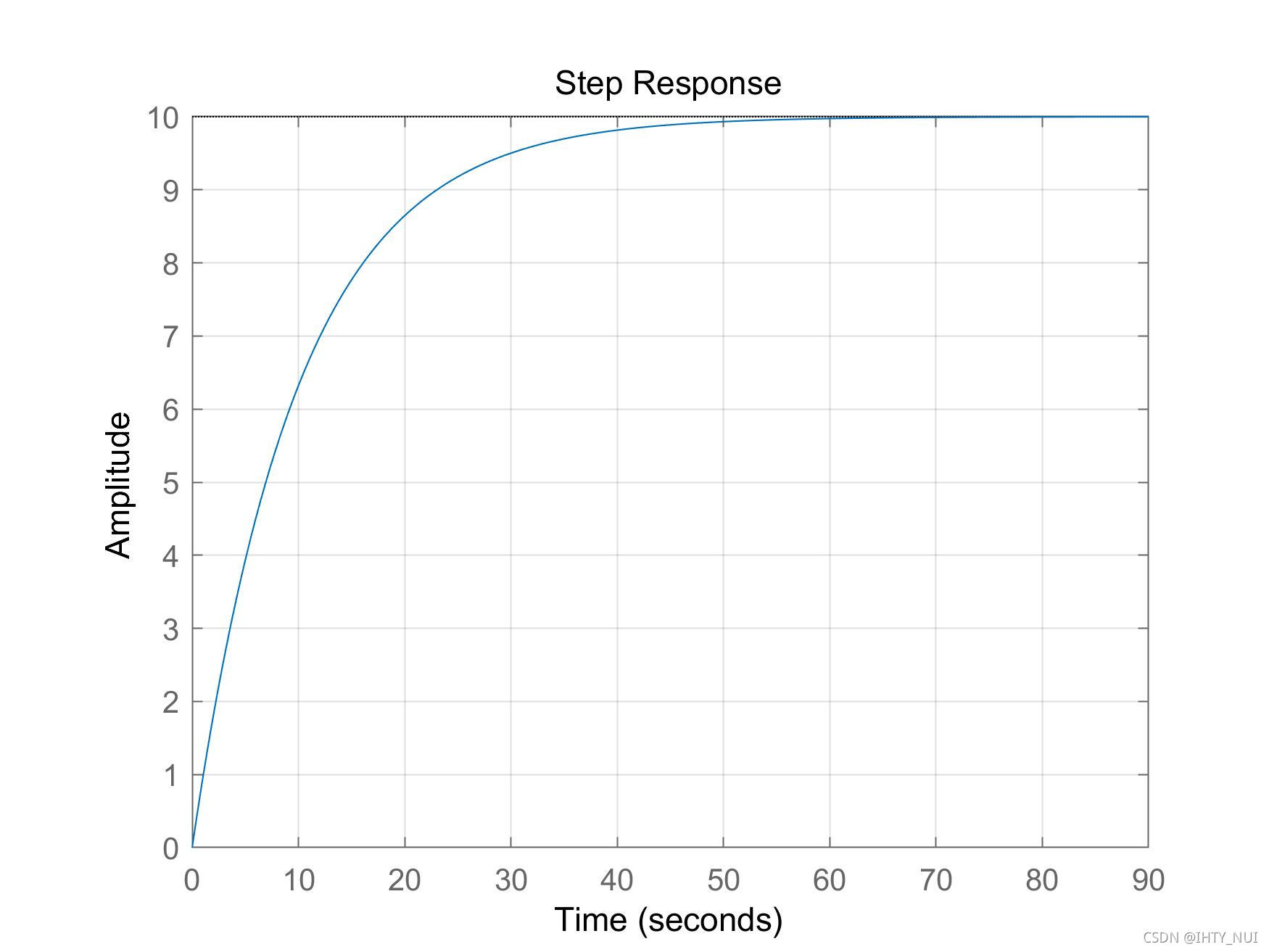
阶跃响应
我们可以使用以下MATLAB命令计算对节约输入u uu的系统时间响应：

k_dc = 5;
Tc = 10;
u = 2;

s = tf('s');
G = k_dc/(Tc*s+1)

step(u*G)

阶跃响应图：
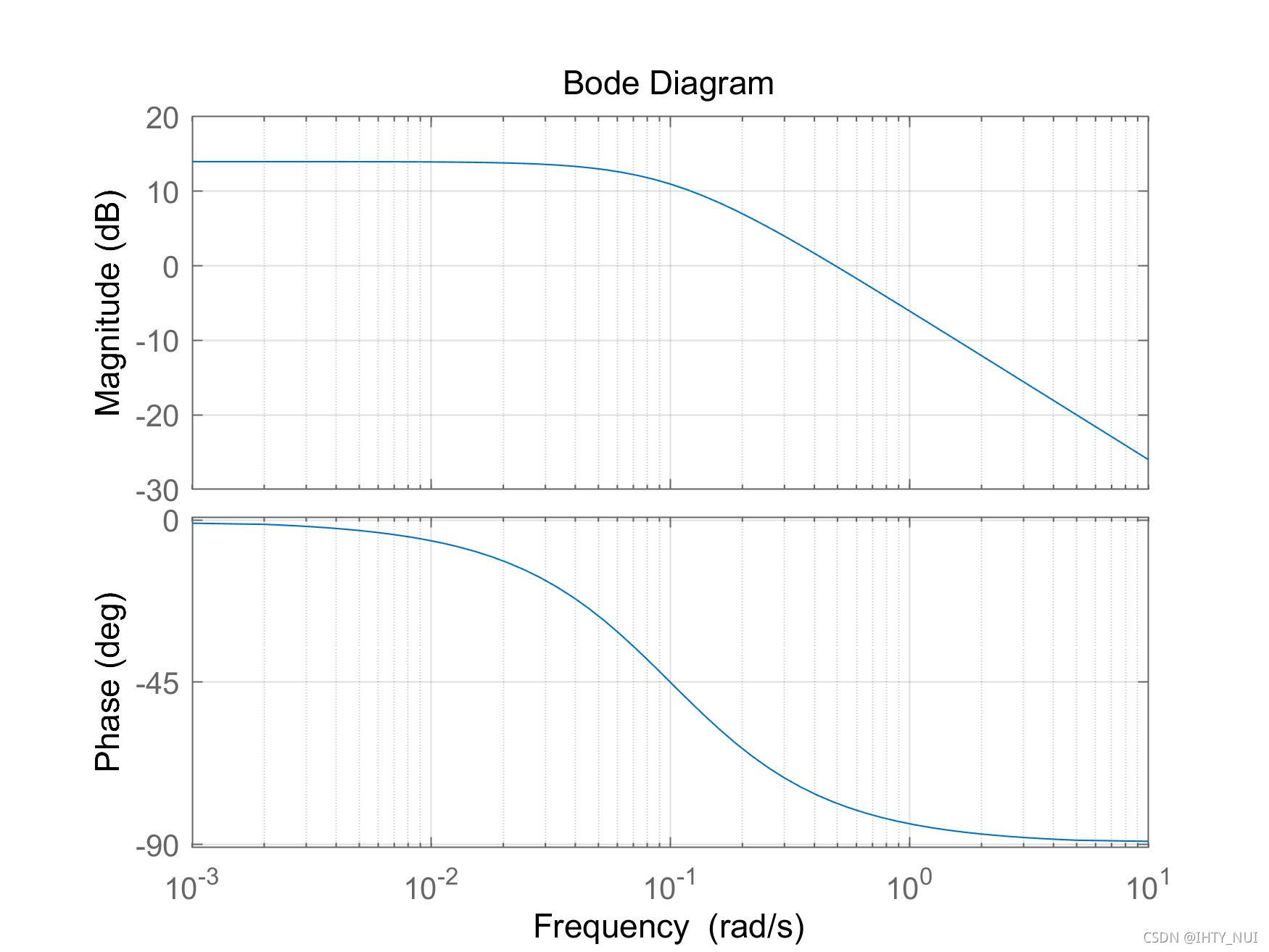
在这里插入图片描述

伯德图：

bode(G)

在这里插入图片描述
伯德图采用对数频率标度，因此可以看到更大的频率范围。同样，使用对数分贝单位(dB)表示幅度，定义为：

$M_{dB}=20log_{10}(M)$

与频率轴一样，分贝标度使我们可以再单个图上查看更大范围的幅度。同样，正如我们将在后续教程中看到的那样，当模块与控制器串联放置时，整个系统的传递函数是各个传递函数的乘积，使用dB标度，整个系统的幅度图就是各个传递函数的幅度图的总和。整个系统的相位图也是各个相位图的总和。

在后续控制器设计的频率方法部分，我们将看到如何使用伯德图来计算闭环稳定性和反馈系统的性能。

二阶系统

二阶系统在实践中经常会遇到，并且是显示振荡的最简单的动态系统类型。例如包括质量块弹簧阻尼器系统和RLC电路，实际上，许多真实的高阶系统可以近似为二阶以便于分析。
二阶微分方程的规范形式如下：

$m y^{''} + b y^{'} + k y = f (t)$

规范的二阶函数具有以下形式，其中具有两个极点且没有零点。

$G(s)=\frac{1}{ms^2+bs}=\frac{k_{dc}w^2_n}{s^2+2\zeta w_ns+w^2_n}$

其中， $k_{dc}=\frac{1}{k}$ ， $\zeta=\frac{b}{2\sqrt{km}}$ ， $w_n=\sqrt{\frac{k}{m}}$ ，参数 $k_{dc}$ 、 $\zeta$ 、 $w_n$ 表征了典型二阶系统的行为。

零极点
规范的二阶传递函数有两个极点：

$s_p=-\zeta w_n\pm jw\sqrt{1-\zeta^2}$

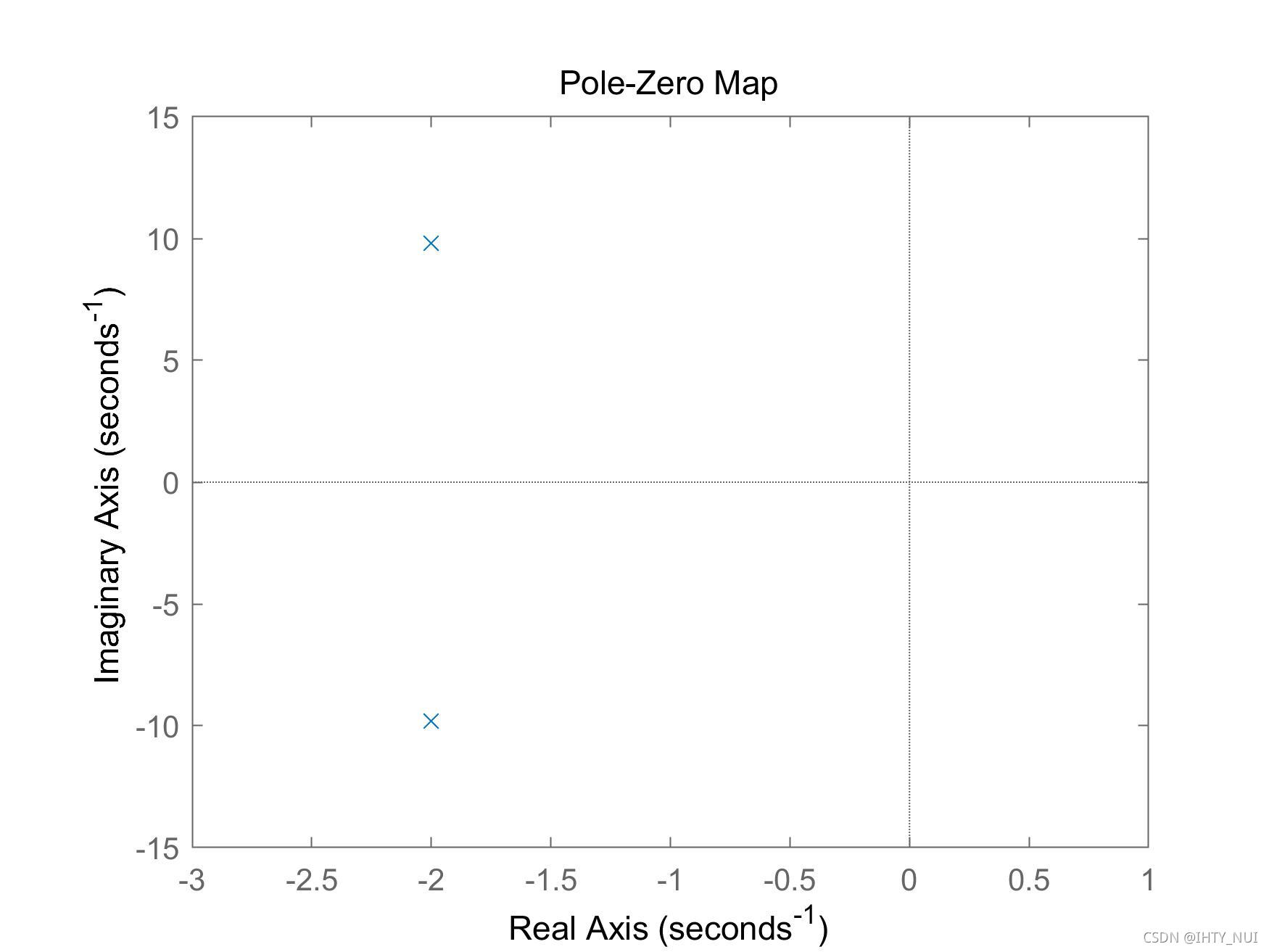
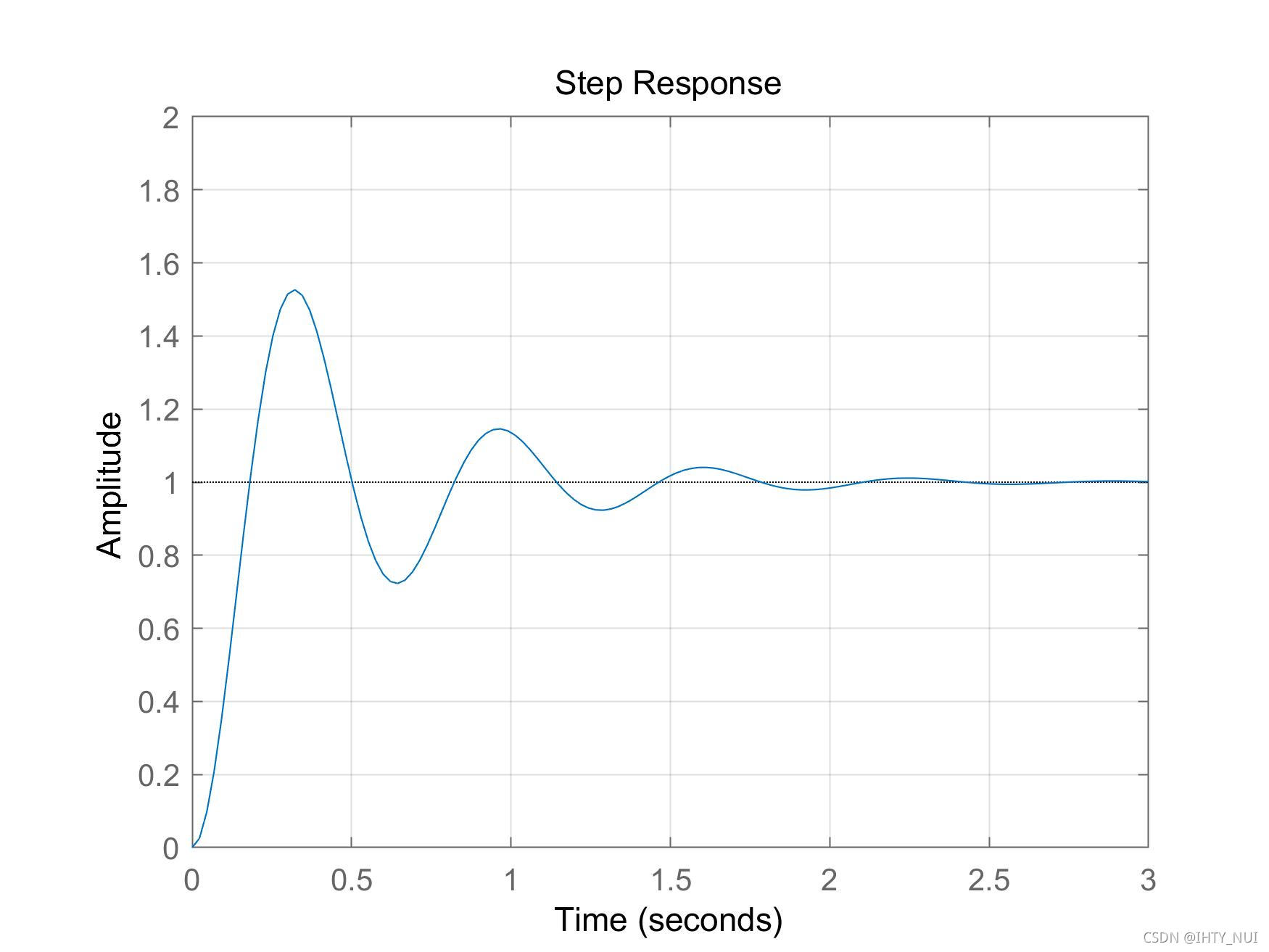
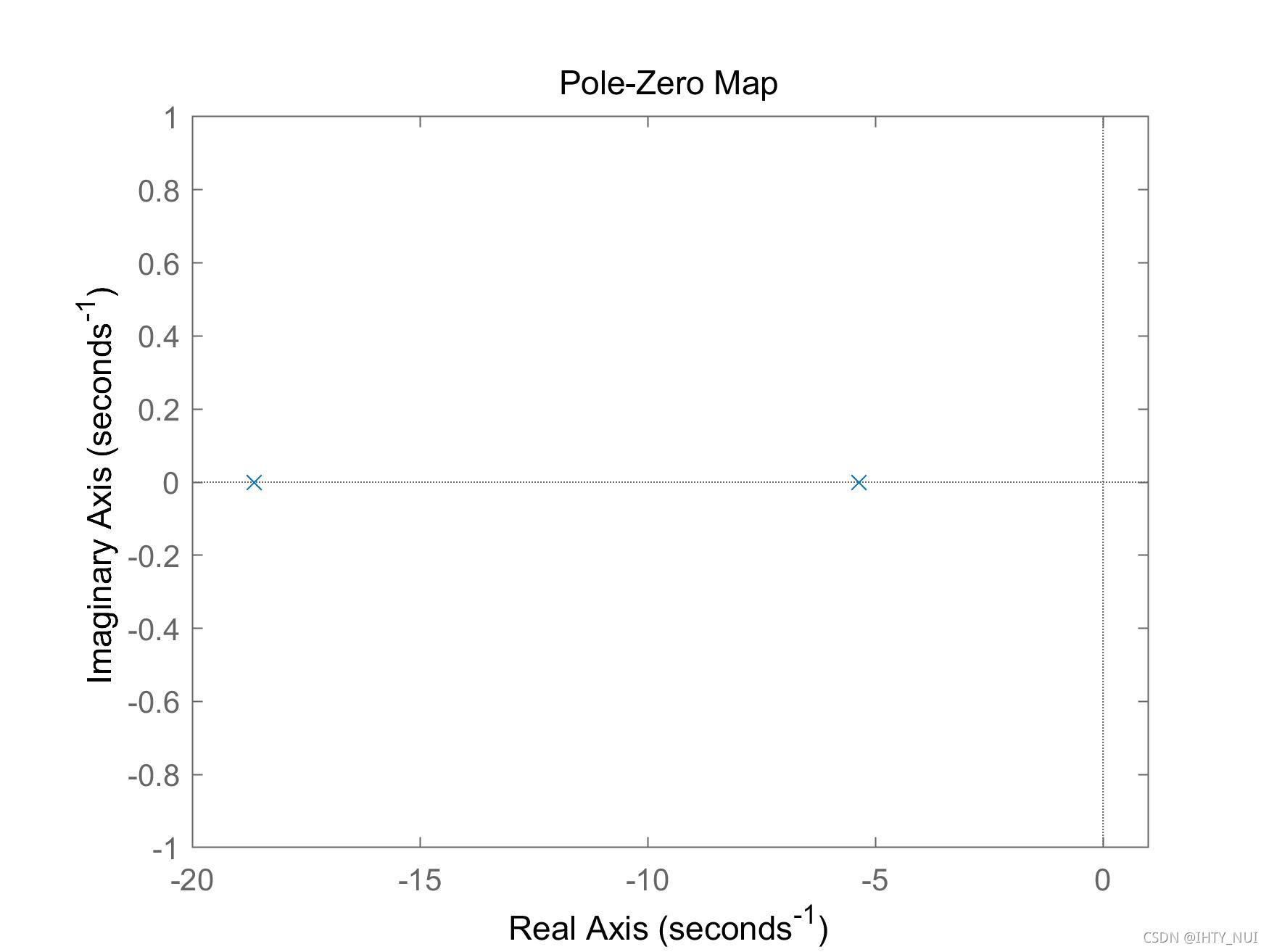
欠阻尼系统
如果 $\zeta <1$ ，则系统阻尼不足，在这种情况下，两个极点都具有负实数的复值，因此，系统是稳定的，但在接近稳态值时会震荡。

k_dc = 1;
w_n = 10;
zeta = 0.2;

s = tf('s');
G1 = k_dc*w_n^2/(s^2 + 2*zeta*w_n*s + w_n^2);

pzmap(G1)
axis([-3 1 -15 15])

零极点图：
在这里插入图片描述

step(G1)
axis([0 3 0 2])	%

阶跃响应图：
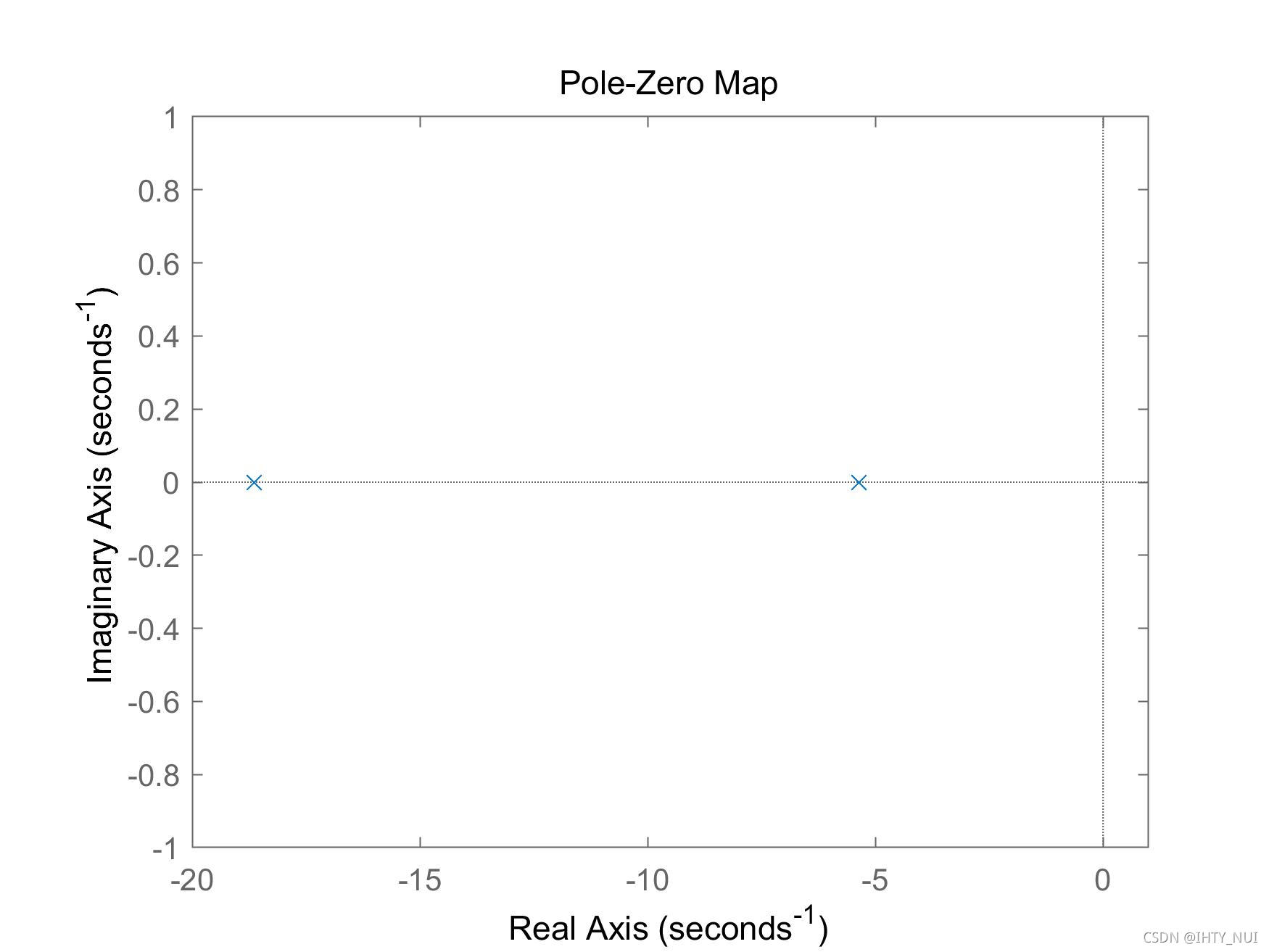
在这里插入图片描述

过阻尼系统
如果 $\zeta >1$ ，则系统属于过阻尼系统，两个极点的实部都是负数，因此，系统是稳定的，不会振荡。过阻尼系统的阶跃响应和零极点图如下所示：

zeta = 1.2;

G2 = k_dc*w_n^2/(s^2 + 2*zeta*w_n*s + w_n^2);

pzmap(G2)
axis([-20 1 -1 1])

零极点图：
在这里插入图片描述

step(G2)
axis([0 1.5 0 1.5])

阶跃响应图：
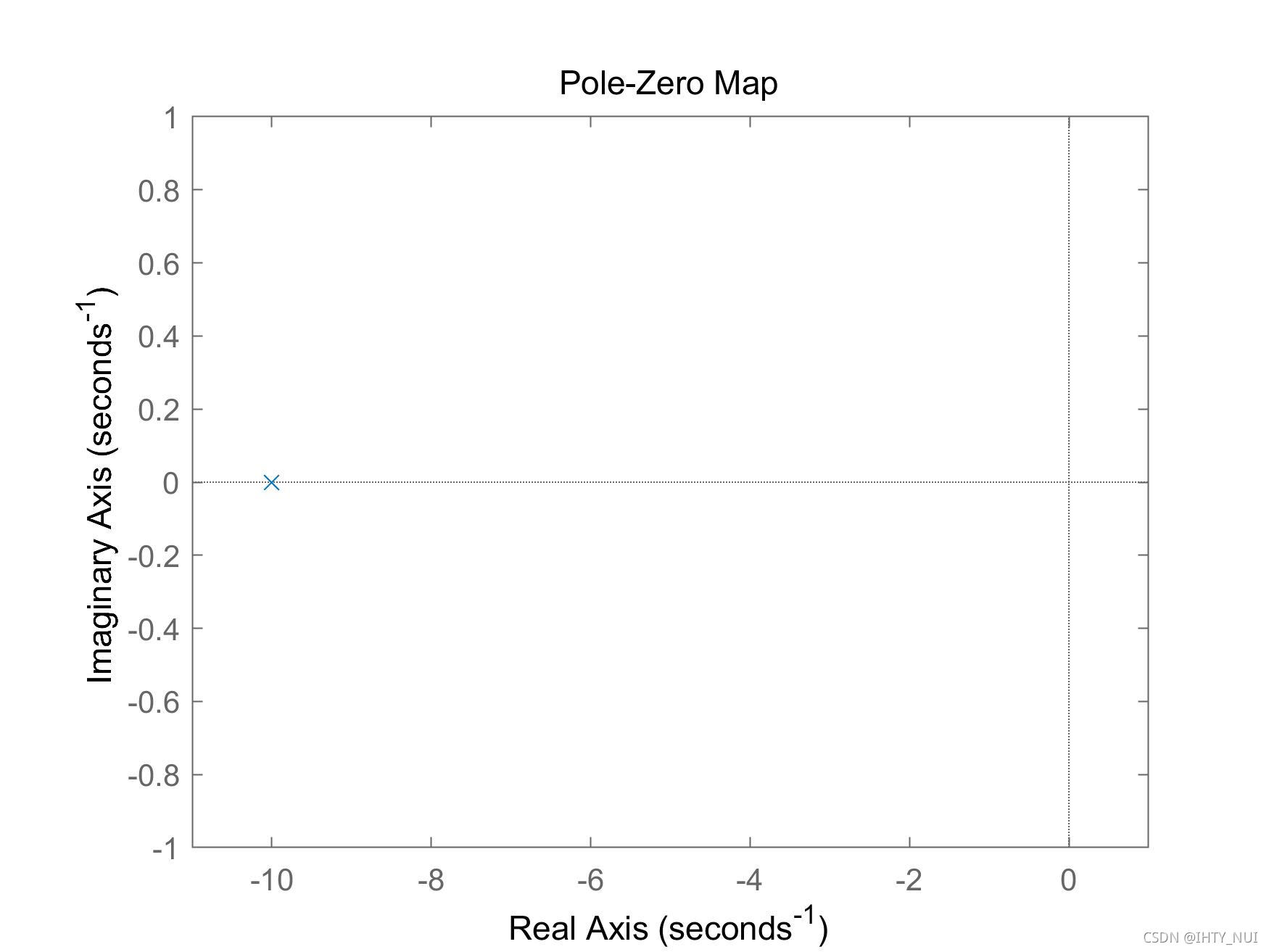
在这里插入图片描述

临界阻尼系统
如果 $\zeta =1$ ，则系统是临界阻尼系统，两个极点相等并都在实轴上，对于规范的二阶系统，当系统处在临界阻尼时，可实现最快的建立时间。现在，将阻尼比设置为1，然后重新绘制阶跃响应曲线和零极点图：

zeta = 1;

G3 = k_dc*w_n^2/(s^2 + 2*zeta*w_n*s + w_n^2);

pzmap(G3)
axis([-11 1 -1 1])

零极点图：
在这里插入图片描述

step(G3)
axis([0 1.5 0 1.5])

阶跃响应图：
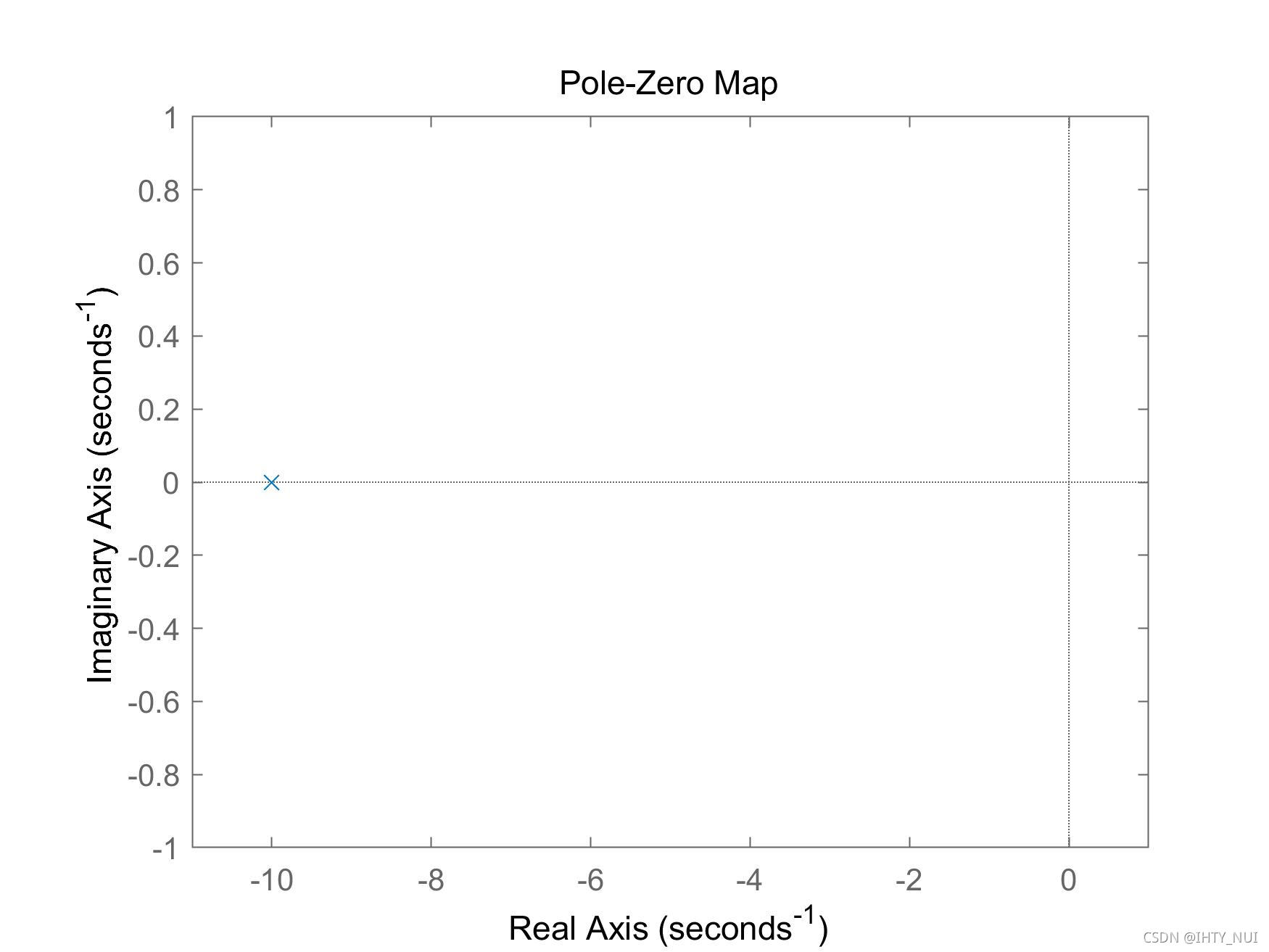
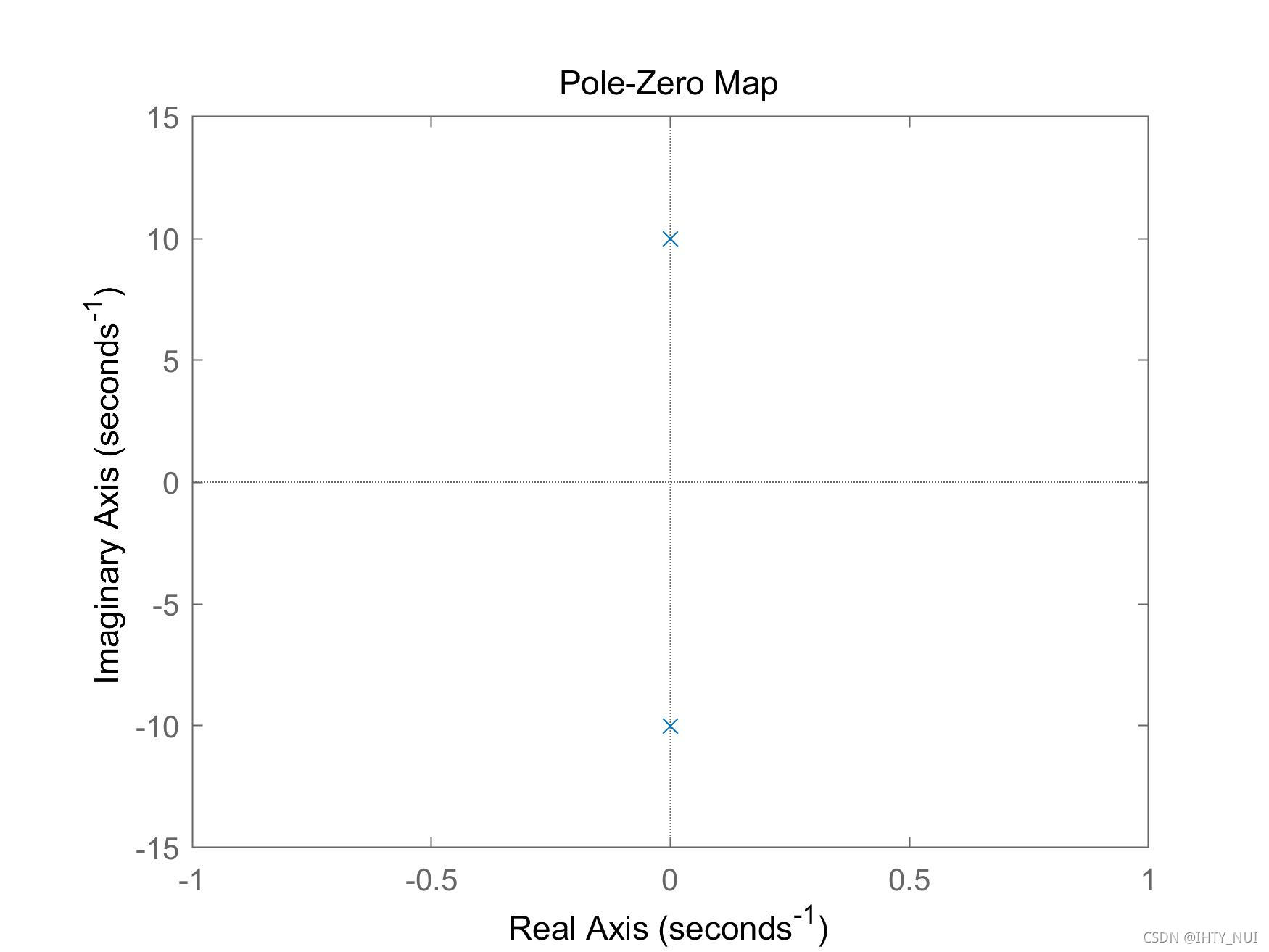
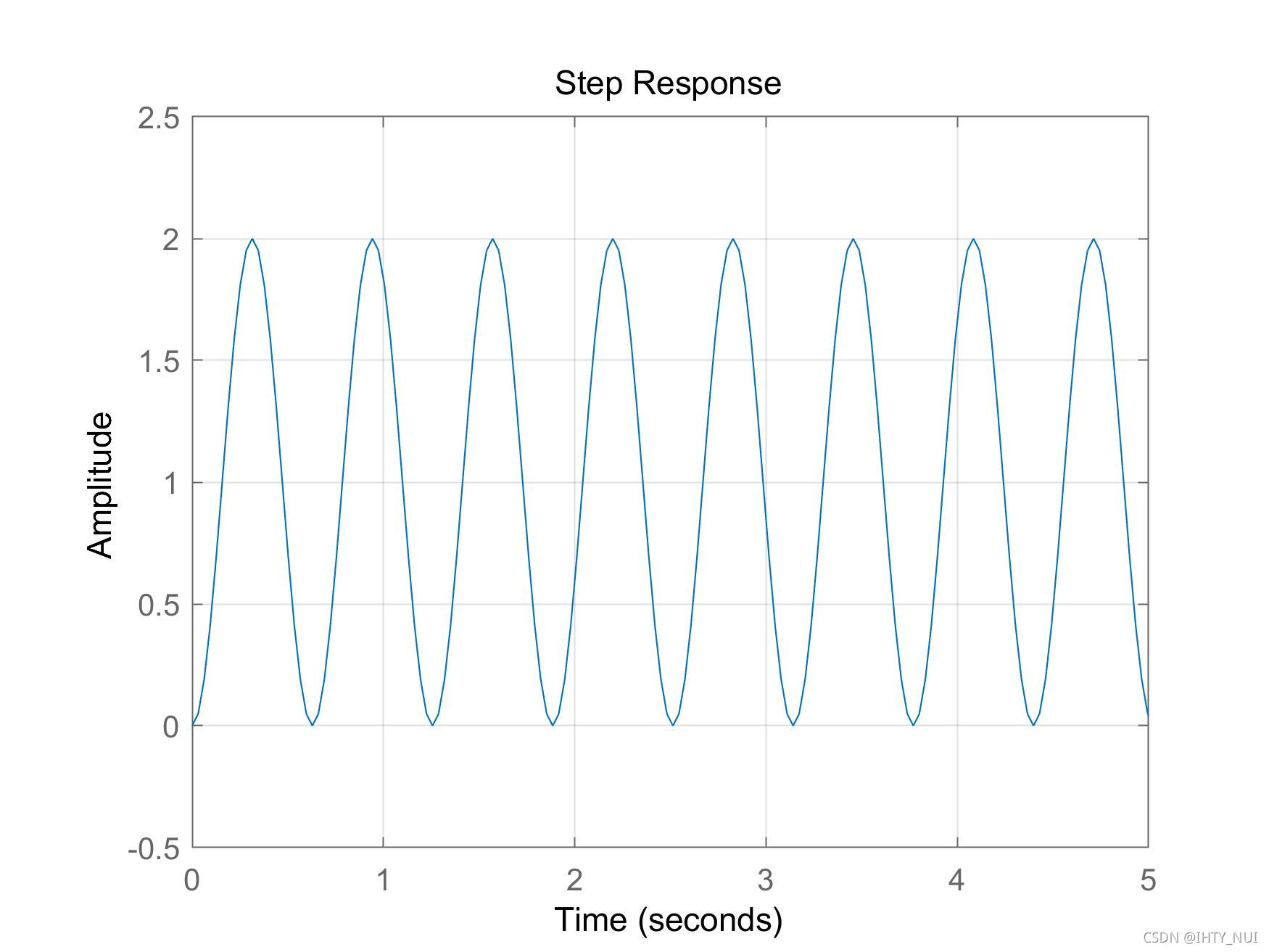
请添加图片描述

无阻尼系统
如果 $\zeta =0$ ，则系统是无阻尼系统，在这种情况下，极点都在虚轴上，因此，系统是稳定的，阶跃响应会无限振荡。

zeta = 0;

G4 = k_dc*w_n^2/(s^2 + 2*zeta*w_n*s + w_n^2);

pzmap(G4)
axis([-1 1 -15 15])

零极点图：
请添加图片描述

step(G4)
axis([0 5 -0.5 2.5])

阶跃响应图：
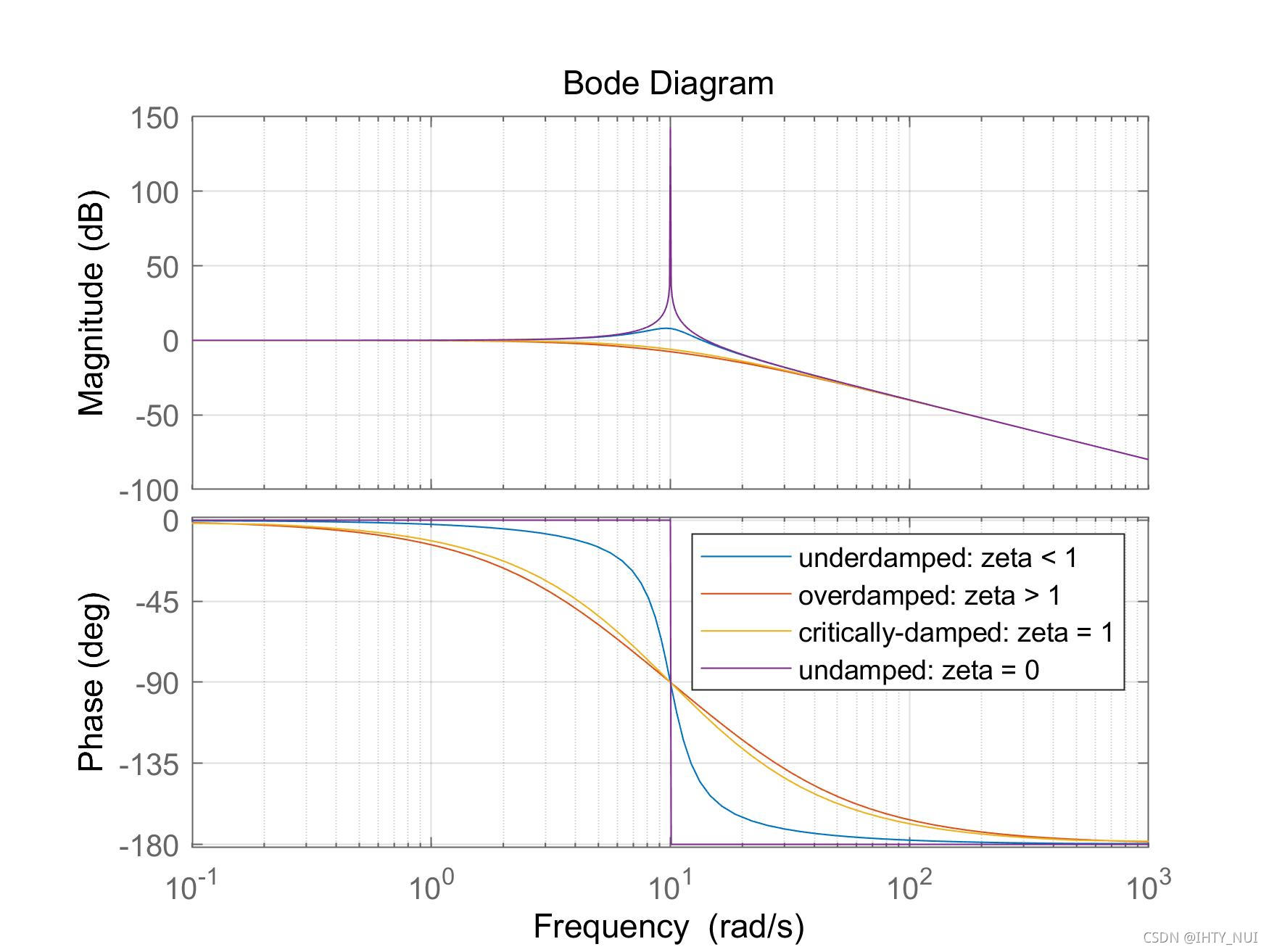
请添加图片描述
伯德图
我们在下面显示了二阶系统所有阻尼条件的伯德幅值图和相位图：

bode(G1,G2,G3,G4)
legend('underdamped: zeta < 1','overdamped: zeta > 1','critically-damped: zeta = 1','undamped: zeta = 0')

请添加图片描述

————————————————
版权声明：本文为CSDN博主「浩子_up」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/zh471021698/article/details/105844194