一.位运算基础
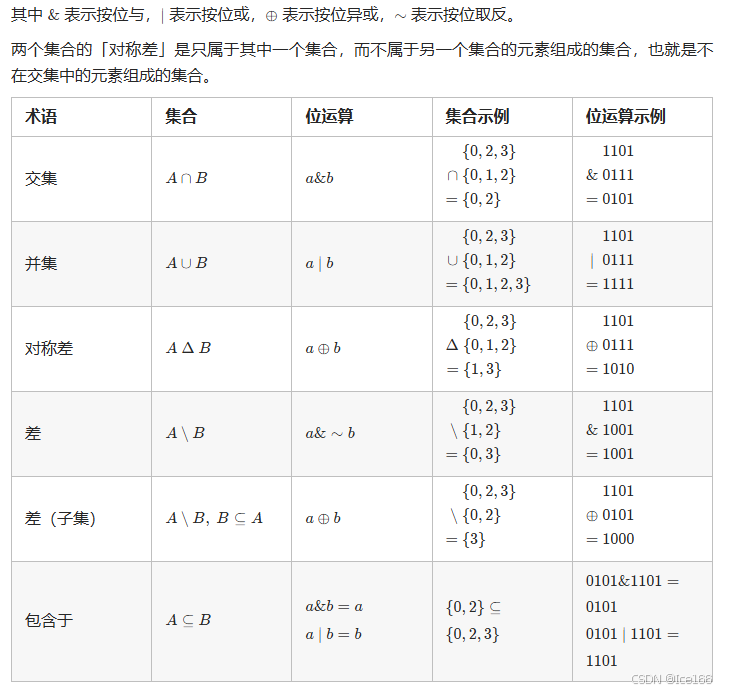
集合与集合之间的位运算
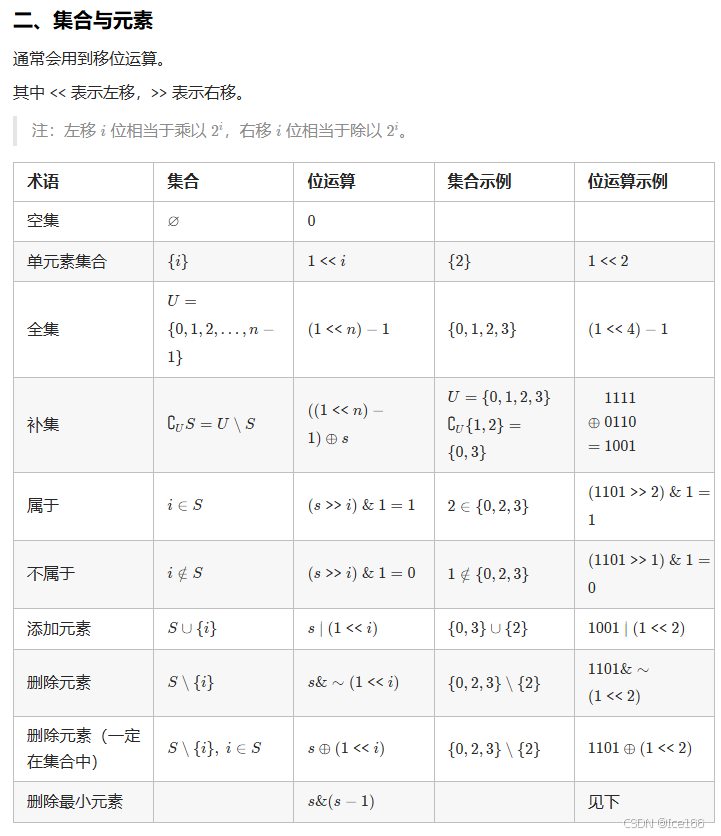
集合和元素
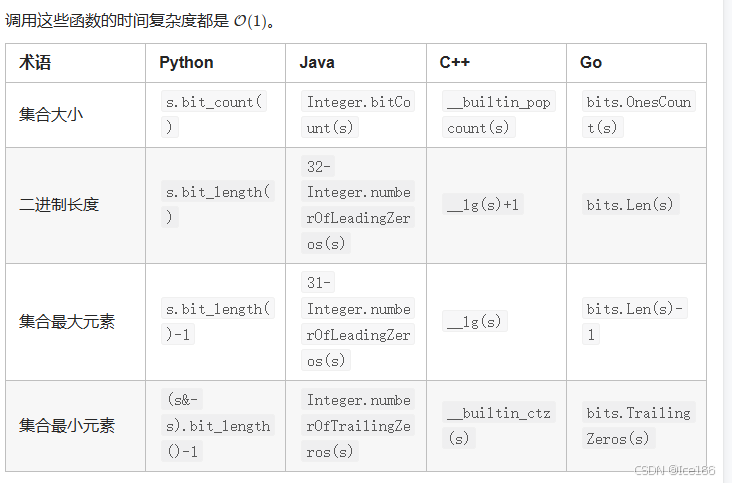
常用函数
1.使两个整数相等的位更改次数
给你两个正帧数 n 和 k,你可以选择 n 的二进制表示 中任意一个值为 1 的位,
并将其改为0,返回使得 n 等于 k 所需要的更改次数,如无法实现,返回 -1
class Solution {
public int minChanges(int n, int k) {
//怎么能这么牛逼,如果是这种题 可以将n和k都换算成二进制数组
//然后如果k不是n的子集 那么就是-1 是子集的话就去掉交集之后数组的长度就是需要操作的次数
//二进制数组取交集 就是 & 运算算
//java算二进制数组的长度有工具类 Integer.bitCount
//取数组差集 子集就是 ^运算
//答案为从 n 中去掉 k 后的集合大小,即 n^k 的二进制中的 1 的个数
return (n & k) != k ? -1 : Integer.bitCount(n ^ k);
}
}2.根据数字二进制下 1 的数目排序
给你一个整数数组 arr,请你将数组中的元素按照其二进制表示中数字 1 的数目进行升序
如果存在多个数字二进制中1的数目相同,则必须按照它们原数值大小升序排序
请你返回排序后的数组
class Solution {
public int[] sortByBits(int[] arr) {
//脑子不好使 确实,因为元素的大小是< 10^4
//那么为了保证相同前提下用原元素大小来作为比较
//可以用结果*100000(防止数据冲突) + 原始数据
//这样在相同情况下原始数据大的肯定在前面
//主要还是本题是返回排序后的数组
//所以最后再%=100000jiu haol
for (int i = 0; i < arr.length; i ++) {
arr[i] += Integer.bitCount(arr[i]) * 100000;
}
Arrays.sort(arr);
for (int i = 0; i < arr.length; i++) {
arr[i] %= 100000;
}
return arr;
}
}3.汉明距离
两个整数之间的 汉明距离 指的是这两个数字对应二进制位不同的位置的数目
给你两个整数 x 和 y,计算并返回他们之间的汉明距离
class Solution {
public int hammingDistance(int x, int y) {
//是不是取对称差?
// return Integer.bitCount( x ^ y);
//用右移实现 每次取不同偏移位的二进制位 不同+1
int count = 0;
for (int i = 0; i < 32; i++) {
//&运算相当于是取最右地位的二进制位数 因为&1=本身
int a = (x >> i) & 1;
int b = (y >> i) & 1;
//^运算是相同为0,不同为1 那么如果是不同直接+1
count += (a ^ b);
}
return count;
}
}4.转换数字的最少位翻转次数
一次 位翻转 定义为将数字 x 二进制中的一个位进行 翻转操作,即将 0-->1,1 -->0
比方说,x = 7,二进制表示为 111,我们可以选择任意一个位(包含没有显示的前导0)
并进行翻转,比方说我们可以翻转最右边一位得到110,或者翻转右边起第二位得到101,
获取翻转右边起第五位(这一位是前导0)得到10111等等操作
给你两个整数start 和 goal,请你返回将 start 转变为 goal 的最少位翻转次数
class Solution {
public int minBitFlips(int start, int goal) {
//这一题应该是根上一题一样,求两个数之间二进制位不相同的个数
//方法一 直接用Java api计算两个数的子集二进制数个数
// return Integer.bitCount(start ^ goal);
//方法二 还是用右移偏移位来计算每个位置的不同
int count = 0;
for (int i = 0; i < 32; i++) {
int x = (start >> i) & 1;
int y = (goal >> i) & 1;
count += (x ^ y);
}
return count;
}
}二.异或 XOR (^)
亦或的性质:
- 相同异或为0,不同为1
- 任意数值与0异或,结果为数值本身
- 异或本身满足交换律,比如:
a = b ^ c ,
a ^ c = b ^ c ^ c
a ^ c = b ^ 0
a ^ c = b
1.数组亦或操作
给你两个整数 n 和 start
数组 nums 定义为:nums[i] = start + 2 * i(下标从0开始),且 n == nums.length
请返回 nums中所有元素按位异或后得到的结果
class Solution {
public int xorOperation(int n, int start) {
int[] ans = new int[n];
for (int i = 0; i < n; i++) {
ans[i] = start + 2 * i;
}
int num = 0;
for (int x : ans) {
num ^= x;
}
return num;
}
}2.解码亦或后的数组
未知整数素组 arr由 n个非负整数组成
经编码后变为长度为 n - 1 的另一个整数数组encoded,其中encoded[i] = arr[i] ^ arr[i + 1]
例如:arr = [1, 0 , 2, 1]编码后得到encoded = [1, 2, 3];
给你编码后的数组 encoded 和原数组arr的第一个元素 first
请解码返回原数组 arr,可以证明答案唯一并存在
class Solution {
public int[] decode(int[] encoded, int first) {
int len = encoded.length + 1;
int[] arr = new int[len];
/**
由题目可知
encoded[i] = arr[i] ^ arr[i + 1]
那么根据异或性质可知
encoded[i - 1] = arr[i - 1] ^ arr[i]
encoded[i - 1] ^ arr[i - 1] = arr[i - 1] ^ arr[i] ^ arr[i - 1]
encoded[i - 1] ^ arr[i - 1] = arr[i];
所以
arr[i] = arr[i - 1] ^ encoded[i - 1]
*/
arr[0] = first;
for (int i = 1; i < len; i++) {
arr[i] = arr[i - 1] ^ encoded[i - 1];
}
return arr;
}
}3.找出前缀异或的原始数组
给你一个长度为 n 的整数数组 pref,找出并返回满足下述条件且长度为 n 的数组 arr
pref[i] = arr[0] ^ arr[1] ^ arr[2] ^ ..... ^ arr[i]
可以保证答案唯一
class Solution {
public int[] findArray(int[] pref) {
/**
根据异或性质
pref[0] = arr[0]
pref[1] = arr[0] ^ arr[1]
pref[1] ^ arr[0] = arr[0] ^ arr[1] ^ arr[0] = arr[1]
那么
pref[2] = arr[0] ^ arr[1] ^ arr[2]
pref[2] ^ arr[0] = arr[1] ^ arr[2]
pref[2] ^ arr[0] ^ arr[1] = arr[2]
而arr[0] ^ arr[1] 是=pref[1]的由上面可知
所以
pref[2] ^ pref[1] = arr[2]
所以
arr[0] = pref[0]
arr[1] = pref[1] ^ arr[0] = pref[1] ^ pref[0]
arr[i] = pref[i] ^ pref[i - 1]
*/
int[] arr = new int[pref.length];
arr[0] = pref[0];
for (int i = 1; i < pref.length; i++) {
arr[i] = pref[i] ^ pref[i - 1];
}
return arr;
}
}4.只出现一次的数字
给你一个非空整数数组 nums,除了某个元素只出现一次外,其余每个元素均出席那两次
找出那个只出现一次的元素
你必须设计并实现线性时间复杂度的算法来解决此问题,且只使用常量额外空间
class Solution {
public int singleNumber(int[] nums) {
// ^运算
/**
2 ^ 2 ^1 = (2 ^ 2) ^ 1 = 1
4 ^ 1 ^ 2 ^ 1 ^ 2 = 4 ^ (1 ^ 1) ^ (2 ^ 2) = 4 ^ 0 ^ 0 = 4
直接用异或就是了 因为根据异或的性质 异或本身 = 0
*/
int ans = 0;
for (int num : nums) {
ans ^= num;
}
return ans;
//用哈希咯?
// Map<Integer, Integer> map = new HashMap<>();
// //额外常量空间 那么就还可以用二进制来表示了
// //
// for (int i = 0; i < nums.length; i++) {
// int num = map.getOrDefault(nums[i], 0) + 1;
// map.put(nums[i], num);
// }
// for (int key : map.keySet()) {
// if (map.get(key) == 1) return key;
// }
// return -1;
}
}三. 与或(&、|)
&的数越多,结果越小,|的数越多,结果越大
&:遇0则0
|:遇1则1
1. 检查按位或是否存在尾随零
给你一个正整数数组nums
你需要检查是否可以从数组中选出两个或更多元素,满足这些元素的按位或运算结果的二进
制表示中至少存在一个尾随零
例如:数字5的二进制表示为101,不存在尾随零,数字4是100,存在两个尾随零
如果可以选择两个或更多元素,其按位或运算结果存在尾随零,返回true,否则返回false
class Solution {
public boolean hasTrailingZeros(int[] nums) {
//草 真牛逼 | 是遇1则1 尾随0 那么最低为如果要为0则肯定不能是1
//也就是说不能是奇数,因为奇数的最低位肯定是1 那么|的结果肯定最低位都是1
//所以要用用& 如果存在尾随0,那么结果肯定=0
//也就是说只要找出有两个及以上的偶数就满足
int count = 0;
for (int num : nums) {
if ((num & 1) == 0) count++;
}
return count >= 2;
}
}4.其他
1.质数的最大距离
给你一个整数数组nums
返回两个(不一定不同的)质数在nums中下标的最大距离
class Solution {
public int maximumPrimeDifference(int[] nums) {
//质数是只能被1和本身整除,在一定范围内 如果能被10以内的某个数整除(1除外)这个就不就是质数 反之就是质数
//所以写一个判断质数的方法
//然后一个从前遍历 找到第一个质数 一个从后遍历找到最后一个质数
//两者下标就是最大距离
int i = 0;
while (!isPrime(nums[i])) {
i++;
}
int j = nums.length - 1;
while (!isPrime(nums[j])) {
j--;
}
return j - i;
}
private boolean isPrime(int n) {
for (int i = 2; i * i <= n; i++) {
if (n % i == 0) return false;
}
return n >= 2;
}
}