Introduction

激活函数（activation function）层又称 非线性映射 (non-linearity mapping) 层，作用是 增加整个网络的非线性（即 表达能力 或 抽象能力）。

深度学习之所以拥有 强大的表示能力 ，法门便在于 激活函数 的 非线性 。 否则，就算叠加再多的线性卷积，也无法形成复杂函数。

然而物极必反。由于 非线性设计 所带来的一系列 副作用（如 期望均值不为0、死区），迫使炼丹师们设计出种类繁多的激活函数来 约束 非线性 的 合理范围 。

由于激活函数接在bn之后，所以激活函数的输入被限制在了 (-1, 1) 之间。因此，即使是relu这种简易的激活函数，也能很好地发挥作用。

激活函数类型

激活函数中，常用的有Sigmoid、tanh(x)、Relu、Relu6、Leaky Relu、参数化Relu、随机化Relu、ELU。

其中，最经典的莫过于 Sigmoid函数 和 Relu函数 。

Sigmoid

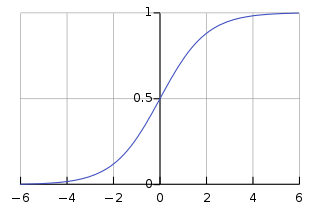
Sigmoid函数，即著名的 Logistic 函数。

被用作神经网络的阈值函数，将变量映射到 (0，1) 之间：

$$S(x)=\frac{1}{1+e^{-x}}$$

其导数为：

$$S^{\prime }(x)=S(x)[1-S(x)]$$

缺陷：

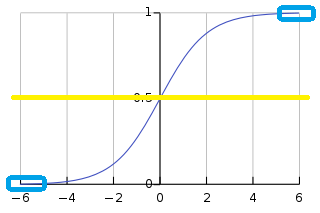
1. 输出值落在(0, 1)之间，期望均值为 0.5 [黄线]，不符合 均值为 0 的理想状态。
2. 受现有的梯度下降算法所限（严重依赖逐层的梯度计算值），Sigmoid函数对落入 (-∞，-5) ∪ (5，+∞) 的输入值，梯度 计算为 0，发生 梯度弥散。因此该函数存在一正一负 两块“死区”[蓝框区域]：

tanh(x)

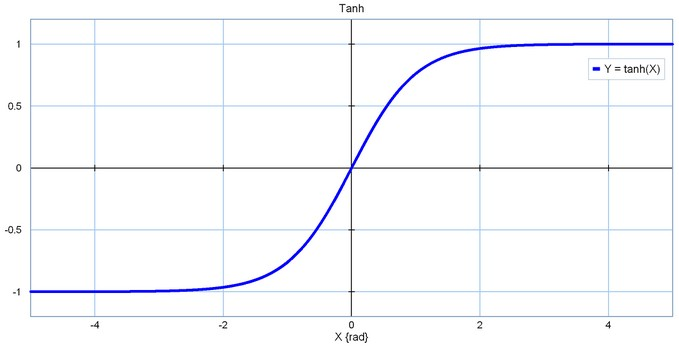
tanh是双曲函数中的一种，又名 双曲正切 ：

$$\tanh (x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}=2S(2x)-1$$

贡献

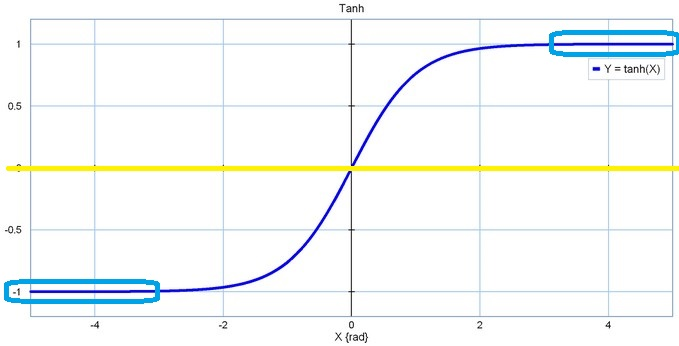
1. 将 期望均值 平移到了 0[黄线]这一理想状态。

缺陷

1. 本质上依然是Sigmoid函数，依然无法回避一左一右两块 “死区”[蓝框区域]（此时“死区”甚至还扩张了区间范围）：
   

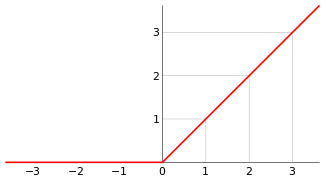
Relu

Relu函数，Rectified Linear Unit，又称 修正线性单元 ：

$$f(x)=\max (0,x)$$

Relu设计已成为了当下的标配。

当下和relu相关的两大标配：

• He初始化 (对relu网络有利)；
• conv->bn->relu (默认采用relu)。

贡献

1. 彻底 消灭 了 正半轴上 的 死区；
2. 计算超简单；
3. 正是因为AlexNet中提出了Relu，在当时很好地缓解了梯度弥散，使得网络深度的天花板第一次被打破；
4. 该设计有助于使模型参数稀疏。

缺陷

1. 期望均值 跑得离 0 更远了；
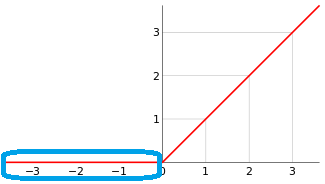
2. 负半轴上 的 死区[蓝框区域]直接蚕食到了 0点 。
   

Relu6

由于 Relu 函数 的 正半轴 不施加任何非线性约束，因此当输入为 正大数 时，易引起 正半轴上 的 梯度爆炸 。因此，Relu6 应运而生：

$$f(x)=\min (\max (0,x),6)$$

贡献

1. 对 正半轴 施加了 非线性约束；
2. 计算超简单。

缺陷

1. 期望均值 依然不为 0 ；
2. 正半轴上 的 死区 死灰复燃，从Relu的 (-∞，0) 蚕食至 Relu6的 (-∞，0) ∪ (6，+∞) 。

但是15年bn出来之后，输入被归一化到了 (-1, 1) 之间。因此，relu6的设计就显得没有必要了。

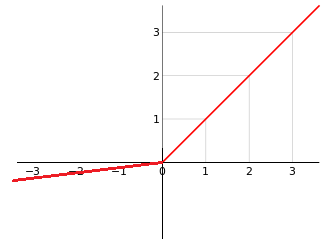
Leaky Relu

对 Relu 函数 新增一 超参数 $\lambda$ ，以解决负半轴的死区问题：

KaTeX parse error: Undefined control sequence: \mbox at position 33: …n{array}{ll}x &\̲m̲b̲o̲x̲{当x≥0时;}\\\lamb…

其中，超参数 $\lambda$ 常被设定为 0.01 或 0.001 数量级的 较小正数 。

贡献

1. 把 负半轴上 的 死区 也端了，从此再无死区；

缺陷

1. 期望均值 依然不为 0 ；
2. 合适的 $\lambda$ 值 较难设定 且较为敏感，导致在实际使用中 性能不稳定 。

参数化Relu

将 Leaky Relu 函数 中的 超参数 $\lambda$ 设置为 和模型一起 被训练到 的 变量，以解决$\lambda$ 值 较难设定 的问题。

贡献

1. 更大自由度。

缺陷

1. 更大的过拟合风险；
2. 较为麻烦。

随机化Relu

将 Leaky Relu 函数 中的 超参数 $\lambda$ 随机设置 。

ELU

ELU函数，Exponential Linear Unit，又称 指数化线性单元 ，于2016年提出。

KaTeX parse error: Undefined control sequence: \mbox at position 33: …n{array}{ll}x &\̲m̲b̲o̲x̲{当x≥0时;}\\\lamb…

其中，超参数 $\lambda$ 常被设定为 1 。

贡献

1. 完美解决了死区问题。

缺陷

1. 期望均值 依然不为 0 ；
2. 计算较复杂。

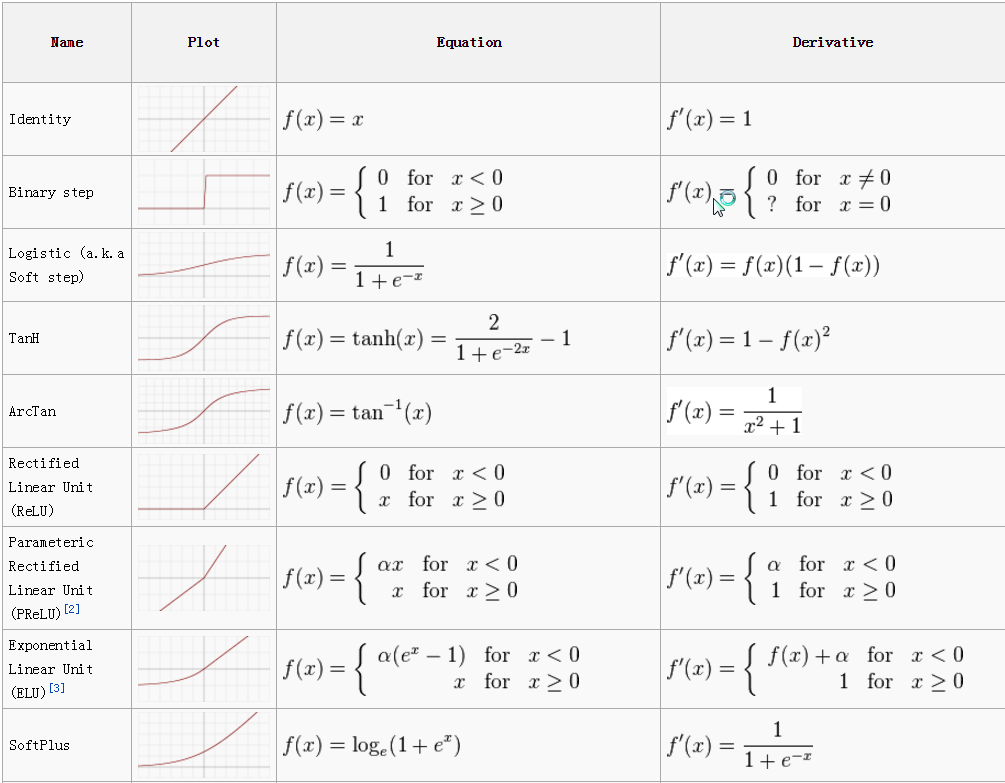
其他函数

下图摘自：【机器学习】神经网络-激活函数-面面观(Activation Function)

Summary

• Every coin has two sides.
• Sigmoid 和 tanh(x) 不建议使用；
• Relu最常用；
• 为了进一步提高模型精度，Leaky Relu、参数化Relu、随机化Relu 和 ELU 均可尝试（但四者之间无绝对的高下之分）。
• “ conv -> bn -> relu ” 套件目前早已成为了CNN标配module。

Test

Tensorflow中激活函数的 API使用 参见我的另一篇文章：tensorflow: 激活函数(Activation_Functions) 探究