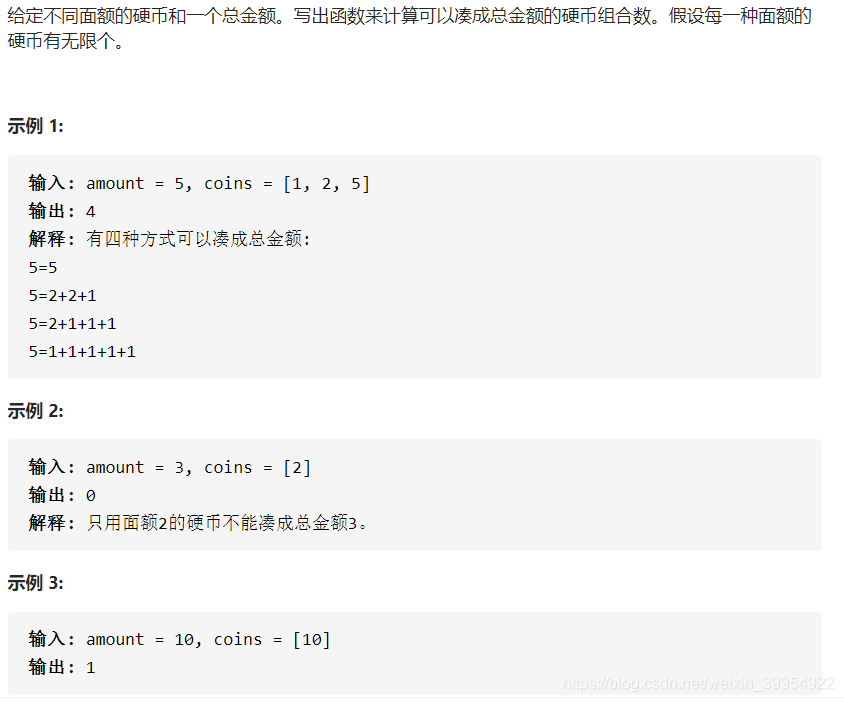
针对动态规划求方案数的题目，有两种题目容易混淆：

题目一：零钱兑换II（https://leetcode-cn.com/problems/coin-change-2/）

题目二：爬楼梯问题(https://leetcode-cn.com/problems/climbing-stairs/)

题目二中，通过分析，可以得知子问题是最后一步是通过跨两个台阶，还是一个台阶上来的。所以动态转移方程为：

dp[i] = dp[i-1] + dp[i-2]

一、注意：以下是错误思路：

通过题目二，我们可以推断出题目一的动态转移方程，无非就是把台阶数换成了硬币面额，而且硬币的种类比较多而已，所以

dp[i] += dp[i-coins[j]]，j = 0~coins.size()-1

所以写出代码：

int dp[amount + 1];//amout是目标面额
dp[0] = 1;
for(int i = 1;i<=amount;i++)//外层是面额
{
	for(int j = 0;j<coins.size();j++)//里面是硬币
	{
		if(i >= coins[j])
			dp[i] += dp[i - coins[j]];
	}
}
return dp[amount];

但是，算出来的结果比真正的结果要多，为什么？因为这么算出来的结果是排列数，而不是组合数，也就是说它把2+2+1和1+2+2认为是不同的两种方案，本质上其实是把子问题搞错了。

二、正确思路：

上面把子问题搞成了凑成一个面额，总共有几种不同的硬币排列方式，而我们想要的真正问题是凑成一个面额，有几种不同的方案。

所以真正的子问题是

dp[i][j] = dp[i-1][j] + dp[i][j-coins[i]]

这里dp[i][j]代表前i个硬币凑成面额j有几种方案，dp[i-1][j]表示当面额j >= coins[i]时，不用当前i去凑面额j的方案数，dp[i][j-coins[i]]表示当j >= coins[i]时，用i去凑面额j的方案数，两者合在一起就是j的方案数。也就是说这道题的一维动态规划的组合数问题其实是二维完全背包问题。

所以动态转移方程为：

如果j >= coins[i]，dp[i][j] = dp[i-1][j] + dp[i][j-coins[j-1]]；
如果j < coins[i]时，dp[i][j] = dp[i-1][j]；

所以代码应该为：

vector<vector<int>> dp(n+1,vector<int>(amount+1,0));
for(int i = 0;i<=n;i++)
dp[i][0] = 1;
for(int j = 1;j<=amount;j++)
dp[0][j] = 0;
if(amount == 0) return 1;
for(int i = 1;i<=n;i++)
{
	for(int j = 1;j<=amount;j++)
    {
     	if(j >= coins[i-1])
        	dp[i][j] = dp[i-1][j] + dp[i][j - coins[i-1]];
        else
            dp[i][j] = dp[i-1][j];
    }
}
return dp[n][amount];

如果用一维数组的话，其子问题应该是：

对于硬币从 0 到 k，我们必须使用第k个硬币的时候，当前金额的组合数

所以如果用一维动态来计算，只需要把那个错误思路的内外循环调换一下顺序即可

for(int i = 0;i<coins.size();i++)//硬币在外层
{
	for(int j = 1;j<=amount;j++)//面额在里层
   	{
         if(j>=coins[i])
         	dp[j] += dp[j-coins[i]];
    }
}
return dp[amount];

二维与一维数组对比：

时间复杂度相同O(M*N)，一维可以降低空间复杂度。

参考：https://leetcode-cn.com/problems/coin-change-2/solution/ling-qian-dui-huan-iihe-pa-lou-ti-wen-ti-dao-di-yo/