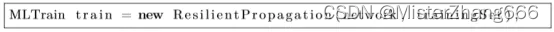回归，分类和聚类在机器学习问题上是三种最主要的数据评估方式，这三种模式是最常见的，也是本节的重点，下面将为你介绍分类，回归和聚类。

一、数据分类

分类尝试确定输入数据所属哪个类别，分类通常是一个监督训练操作，这意味着是用户向神经网络提供数据和期望的结果。对于数据分类，期望结果是确定这个数据类。

监督神经网络总是训练知道的数据，在训练期间，神经网络评估怎样更好地分类已知的数据，一旦训练完成，神经网络期望将能够更好地去分类未知的数据。

Fisher’sIris 数据集是个分类的例子，这个数据集包含了Iris花的测量数据，这是一个最著名的数据集，它经常用来评估机器学习方法，点击下载Iris数据集。

Iris部分示例：

下载下来的数据为一个CSV文件，CSV是一种很常见的神经网络输入数据格式，第一行通常是定义为每个文件的列，如图所示，每种花提供了五种信息：

• Sepal Length (萼片长度) • Sepal Width (萼片宽度) • Petal Length (花瓣长度) • Petal Width (花瓣宽度) • Species (种类)

对于分类，神经网络要求给萼片和花瓣的长/宽, 神经网络就能够识别这个花所属的类别。

一个分类属性通常是一个非数字数据，因此，类中的成员必须是明确定义的，对于这个Iris数据集，有三个不同的Iris类别，如果一个神经网络训练的是这三种Iris类别，那就不能期望它能够识别出除这三个类别外的其他类别。分类的所有成员必须在训练前就已知。

二、回归分析

在上一节，我们学习了怎样分类数据，通常想要的输出不是一个简单的类，而是一个数值，考虑一下这个汽车的每加仑英里 (MPG)的计算，提供的数据，如发动机尺寸和汽车重量，这个汽车也许就能够计算出它的MPG。

考虑以下五辆汽车数据示例：

对于更多的信息，完整的数据集可以在这个网站上找到：

http://www.heatonresearch.com/wiki/MPG_Data_Set

回归的思想是用车辆的输入数据训练神经网络，但是，使用回归时，网络不会生成类，神经网络预计能提供每加仑汽油的里程数。

同样重要的是要注意，并不是上述文件中的每一个数据都将被使用，如“汽车名称”和“原产地”不使用，汽车的名称与燃油效率无关，因此被排除在外。同样，原产地也不利于这个方程，原产地是一个数值，它指定汽车的地理区域。虽然有些地区确实注重燃料效率，但这一数据范围太广，不起作用。

三、聚类

另外一个常用的分析是聚类，不像前两个分析类型，聚类是一个典型的无监督，前两节中的数据集可以应用于聚类，不同的是聚类分析将不要求用户像在Iris数据集的情况下提供物种，或者MPG数据集提供MPG，聚类算法预计将数据元素放置到与物种或者MPG相对应的集群中。

对于聚类，这种机器学习方法简单地查看数据，并试图将这些数据放入多个集群中，预计的集群数量必须提前定义，如果集群数量变化，集群机器学习方法将需要再次训练。

聚类和分类非常相似，它的输出是一个集群，这类似于一个分类，然而，集群不同于回归，因为它不提供一个数字，所以，如果将聚类与MPG数据集一起使用，那输出将是一个汽车可以归入到其中的某个集群，也许每个集群会指定不同级别的车辆燃料效率，也许聚类会把汽车分为几组，显示出一些尚未被注意到的关系。

四、理解神经网络的各层

现在已经对神经网络三个主要模型问题有了了解，是时候来考察数据是怎样提供给神经网络的了，这节将重点主要是在怎样构造一个神经网络接受数据项并提供输出，随后的章节将详细说明数据在提供给神经网络之前如何标准化数据。

神经网络通常是分层的，至少有一个输入和输出层，也许还有隐藏层，某些神经网络类型不会再输入和输出层之外分解成任何形式层，然而，这个输入层和输出层将永远存在，也许可能被整合在同一层，我们现在将考察输入层，输出层和隐藏层。

1 理解输入层
输入层是神经网络的第一层，和其他层一样，这一层包括了一个指定数字的神经元，同一层的神经元都含有相似的属性，通常，对于神经网络将用于分类，回归或聚类的每个属性，输入层将有一个神经元与之对应。

考虑之前的示例，Iris数据集有四个输入神经元，这些神经元指定花瓣的宽度和长度，萼片的宽度和长度，MPG数据集有更多的输入神经元，输入神经元的数目并不总是直接对应于属性的数量，而一些属性的数量将需要不止一个神经元编码，这个编码过程，称为标准化，将在下一章中介绍。

神经元的数量决定了一层的输入结构，对于每个输入神经元，存储为一个double值，例如，以下的数组能够被输入到包含五个神经元的层:

double[]input = new double[5];

这个输入到一个神经网络总是为一个double类型的数组，重要的是这个数组直接对应于输入层神经元的数目，Encog使用MLData接口定义类来持有这些数组，上面的数组能够简单的转换为一个MLData 对象，代码如下:

MLDatadata = new BasicMLData(input);

可提供给encog的数据，是由MLData接口定义任何“array like”数据，输入必须总是使用MLData对象传递给神经网络内部，BasicMLData类实现了MLData接口，然而，BasicMLData类不仅仅是为Encog提供数据的唯一方法，其他实现了MLData的也可以为Encog提供数据。

BasicMLData类仅仅提供了一个基于内存的数据对于神经网络，一旦神经网络处理输出，一个基于MLData类将从神经网络输出层返回，输出层将在下节讨论。

2 理解输出层
输出层是神经网络的最后一层，这层提供了前面那些层处理完的输出，输出层的输出格式非常类似于输入层提供的数据，神经网络的输出是一个double数组。

神经网络输出一个基于MLData接口的类，大多数构建的神经网络返回的输出类型是一个BasicMLData，然而，未来或者第三方神经网络也许会返回其他实现了MLData接口的类型。

神经网络设计接受输入(一个double数组) 和产生一个输出(也是一个double数组)，对于一个神经网络擅长的问题，确定怎样构造输入数据和有意义的输出是两个主要的挑战，神经网络的正真力量来自其模式识别能力，神经网络应该有能力产生想要的输出即使已经发生了扭曲。

回归神经网络通常产生一个输出神经元，他提供神经网络产生的数值，如果相同的神经网络预测到两个或两个以上给定输入的数字，那多输出神经元可能存在。

分类产生一个或多个输出神经元，这取决于输出类怎样编码的，在这里有几个不同的编码方式，将在下一章作详细的讨论。

聚类的设置类似，它的输出神经元确定数据属于哪个集群。

3 隐藏层
在前面的讨论中，神经网络包含了输入层和输出时，有时候，输出层和输入层是相同的，但是大多数通常是两个单独的层，此外，在输入层和输出层之间也许存在其他的层，这层被称为隐藏层，隐藏层在输入层和输出层之间插入，隐藏层也可以承担更多复杂的结构。

隐藏层唯一的目标是让神经网络更好的为给定的输入产生预期的输出，神经网络编程首先涉及到的是定义输入层和输出层神经元个数，一旦确定了如何将编程问题转换为输入和输出神经元数，那是时候来定义隐藏层了。

隐藏层是一个非常大的“黑盒子”，这个问题是根据隐藏层和输出层的神经元数定义的。神经网络如何产生正确的输出部分是通过隐藏层执行的。一旦定义了输入和输出层的结构，就必须定义最佳学习的隐藏层结构。

避免创建一个太简单或者是太复杂的隐藏层结构是一个挑战，太复杂的隐藏层结构将要花太多时间去训练，太简单的隐藏层结构将学习不到这个问题，一个好的起点是一个单一的隐藏层神经元数目等于输入层的两倍，在根据这个网络的性能，隐藏层神经元的数量在适当增加或者减少。

开发者经常想知道该使用多少层隐藏层，一些研究表明，第二个隐藏层是很少的任意值，

Encog是一个很好的方法执行一个实验和错误搜索最优的隐藏层配置，更多的信息，请查看以下的URL：

http://www.heatonresearch.com/wiki/Hidden_Layers

有一些神经网络没有隐藏层，输入层直接连接到输出层，进一步，一些神经网络仅仅只有一个单一的层，那些单一的层是自连的，这些连接允许网络学习，包含在这些连接，成为突触，是一个个体权重矩阵。

五 构造神经网络

这一节将详细地怎样为一个简单的问题构造一个神经网络，设计这样的一个神经网络，它能够模拟一个XOR运算操作，学习XOR运算是神经网络示例中的第一个例子，就像大多数的编程语言的第一个示例是一个简单的“Hello World”显示程序，神经网络时常用这个XOR运算符来做示例，学习XOR运算符是一个神经网络中的”Hello World”程序。

1 XOR操作和神经网络
XOR运算是一种常见布尔逻辑运算符，其他两个是AND和OR运算符，对于每个这些逻辑运算符，有四种不同的组合，AND所有可能的组合如下显示：

0 AND 0 = 0 1 AND 0 = 0 0 AND 1 = 0 1 AND 1 = 0

这应该符合你学习的计算机编程的操作符，正如它的名字所暗示的，仅仅当两个输入都为true的时候，它的运算才返回ture。

OR运算符如下：

0 OR 0 = 0 1 OR 0 = 1 0 OR 1 = 1 1 OR 1 = 1

这也应该和你在计算机编程里学习到的OR运算符是一致的，当输入两个中的其中之一必须为true, OR运算才为true.

“异或”（XOR）运算符不太经常用于计算机编程，XOR运算符的可能组合如下：

0 XOR 0 = 0 1 XOR 0 = 1 0 XOR 1 = 1 1 XOR 1 = 0

正如你看见的，XOR运算仅仅当两个输入都不同时才返回true, 下一节说明怎样为XOR运算构造输入，输出和隐藏层。

2 为XOR构造一个神经网络
这里XOR运算符是两个输入和一个输出，将构造相应的输入和输出结构，给输入神经元喂以下的double值:

上面显示的这些值对应到输入XOR运算符，输出神经元期望的输出为以下的double值:

这是一种神经网络能够构造的而一种方式，这是一种允许一个简单前馈神经网络学习XOR运算符的一种方式，前馈神经网络，也称为感知器，是我们将要学习的第一个神经网络架构。

在这里还有其他的方式将XOR数据传递给神经网络，在本书后面，有两个循环神经网络的示例，探索包括Elman和jordan样式神经网络，这些方法将XOR数据视为一个长序列，基本上连接一起XOR的真值表，结果为一个长的XOR序列：例如：

这里的换行符仅仅是为了可阅读，这种神经网络视XOR为一个长序列，通过使用上面的数据，该神经网络有一个单一的输入神经元和一个单一的输出神经元，输入神经元从上面的列表中得到一个值，输出神经元期望返回这个值的下一个值。

这表明通常有多种方式为一个神经网络提供模型数据，如何为数据建模将大大影响神经网络的成功，如果一个特定的模式不工作，那应该考虑另外一种，下一步就是为前馈神经网络标准化XOR数据。

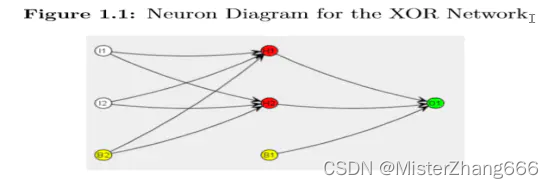
因为XOR运算符有两个输入和一个输出，所以神经网络也跟随这种结构，此外，神经网络有一个单一的隐藏层有两个神经元来帮助处理数据，两个神经元的选择是任意的，经常导致实验和错误，XOR问题是简单的，两个隐藏层神经元足以解决它，这个网络的图入图1.1所示:

在上面网络图中有四个不同的神经元，如下说明：

输入神经元:I1, I2

输出神经元:O1

隐藏神经元:H1, H2

偏执神经元:B1, B2

输入，输出和隐藏神经元在前面已经讨论了，在这个图中看到的新的神经元是偏执神经元，一个偏执神经元总是输出一个为1的值和从不接受从前面层的输入。

简而言之，偏执神经元允许神经网络更有效的学习模式，他们类似隐藏层功能，没有偏执神经元，很难对一个输入值为0的神经网络产生输出，与其说这是XOR数据的一个问题，但它其他数据集也有这个问题，更多有关它功能的详细介绍，可以访问以下URL：

http://www.heatonresearch.com/wiki/Bias

现在看看使用来解决XOR运算符的神经网络代码，完整的代码包含在Encog示例中，位置如下:

Org.encog.examples.neural.xor.XORHelloWorld

示例开始创建一个神经网络如下图1.1.，所需的代码来创建这个网络是相对简单的:

在上面的代码中，一个BasicNetwork被创建，三个层添加到这个网络中，第一层，为输入层，有两个神经元，第二层是隐藏层，也有两个神经元，最后为输入层，有一个神经元，最后，调用finalizeStructure方法通知网络没有层被添加了，调用reset随机初始化这三个层之间的连接权重。

神经网络总是以随机权重值开始。一个训练过程将这些权重调整到提供期望输出的值。由于神经网络总是以随机值开头，所以同一程序的两次运行会产生非常不同的结果。一些随机权重提供了比其他更好的起点。有时随机权重相距太远，网络将无法学习。在这种情况下，权重应该再次随机化，进程重新启动。

你也要注意在上面代码中ActivationSigmoid类，这指定了神经网络使用sigmoid激活函数，激活函数将在第四章中学习，仅仅隐藏层和输出层使用激活函数，输出层没有激活函数，如果一个输入层指定了激活函数，它将没有影响。

每一层都指定了一个boolean 值，boolean值指定了在这个层中是否有偏执神经元，输出层，如图1.1所示，相对于输入层和隐藏层没有偏执神经元，这是因为一个偏执神经元仅仅连接到下一层，输出层是最后一层，所以在这里不需要有偏执神经元，如果一个输出层指定了偏执神经元，他将不起作用。

这些权重构成了长期记忆的神经网络，一些神经网络也包含了上下文层给神经网络的短期记忆，神经网络的学习通过修改这些权重值，这也是真真的Elman和Jordan神经网络。

现在这个神经网络已经被创建，现在应该训练它，训练是一个随机权重被调整到接近输出的过程，训练将在下一节讨论。

3 训练一个神经网络
训练这个神经网络，构造了一个MLDataSet对象，这个对象包括了输入和预期的输出，构造这个对象，有两个数组被创建，第一个数据是XOR运算的输入，第二个是预期的输出，这些将对应于XOR的可能值，回顾一下，四种可能值如下所示:

首先，为XOR构造一个四个输入值的数组，使用了一个两维的double数组，如下:

同样的，也构造一个期望输出的数组，如下:

即使这里仅仅是一个输出值，仍然也需要传递一个二维的数组，如果有多个输出神经元，则像数组额外添加列。

现在构造两个输入数组，必须创建一个MLDataSet对象训练集，这个对象创建如下:

现在训练集已经创建，神经网络能够训练，训练程序调整神经网络权重到最好产生期望输出，训练将继续更多次的迭代指导错误率低于网络可接受的程度，首先，必须创建一个训练对象，Encog支持多种不同类型的训练。

这个例子使用弹性传播训练(RPROP),RPROP也许是encog所支持的最好的训练算法，还提供了其他训练技术，并通过一定的训练技术较好地解决了某些问题，RPROP训练代码构造如下:

所有的训练类实现了MLTrain接口，RPROP算法通过ResilientPropagation类实现，构造如上。

一旦构造了训练器，就应该训练神经网络了，训练神经网络调用的是MLTrain中的iteration方法，直到错误率低于指定的值为止，误差是神经网络输出与期望输出匹配的程度:

上面的代码循环通过更多次的迭代，因为要使神经网络的错误率低于1%，一旦神经网络训练结束，他就真正的使用了，下一节将介绍怎样使用一个神经网络。

4 执行一个神经网络
运用神经网络是调用BasicNetwork类的compute方法，在这里，我们遍历每个训练集值，并显示神经网络的输出:

Compute方法接受一个MLData类和返回另外的MLData对象，返回对象里包含了从神经网络的输出，向用户显示，运行这个程序，每一次迭代的训练结果，当前的错误率首先显示:

第一次迭代的时候错误率为56%，到了107次的时候下降到了1%以下，因为神经网络随机初始化权重，因此有可能每次运行这个程序迭代训练会得到不同的数值，此外，尽管最后错误率也许不同，他也应该总是在1%以下结束。

最终，程序显示每个训练项目的结果如下：

正如你所看见的，这个网络还没有被训练给出准确的结果，这是正常的，因为网络训练为1%的错误率，所以每个结果也将存在一般的1%的预期值。

因为神经网络被初始化随机值，第二次运行这个程序最终的输出也将有差异：

第二次运行输出轻微的不同，这是正常的。

这是第一个Encog示例，在这本书中所有包含的示例能后下载，怎样下载这些示例，更多的信息参考附录A “安装Encog”。

六、总结

Encog是一个先进的机器学习框架，使用来创建神经网络，这章重点在回归，分类和聚类，最后，这章也展示了怎样创建一个能够学习XOR操作的Encog应用程序。

回归神经网络接受输入和产生一个数值型输出，分类神经网络接受输入和预测输入属于哪个类，聚类不要求期望输出，当然，聚类的输入数据和集群输入情况下尽其所能。

Encog支持机种不同的层类型，然而，这些层分为三组，这取决于它们在神经网络中的位置，取决它们在神经网络中的位置，输入层从外部接受输入，隐藏层从输入层接受数据作进一步的处理，输出层从输入或者最后一个隐层得到数据，并输出到外部世界。

XOR运算符是这章中使用的例子，XOR运算符时常使用作为神经网络的简单的“Hello World”应用程序，XOR运算符提供了一个非常简单模式，大多数神经网络能够简单学习，他是重要的知道为一个神经网络怎样构造数据，神经网络接受和返回一个float型数组。

最后，这章详细说明怎样发送数据到一个神经网络，XOR数据示例很容易提供给一个神经网络，没有必要标准化或者编码，然而，大多数真实世界数据将需要标准化，标准化将在下一章介绍。