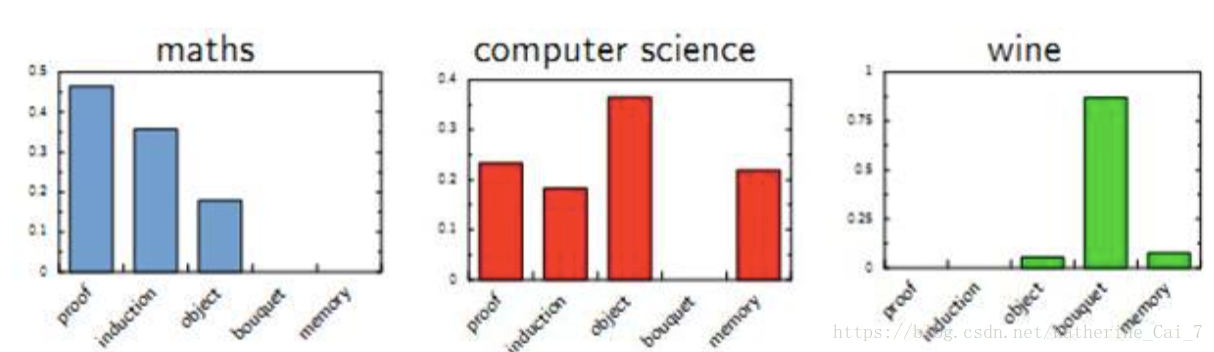
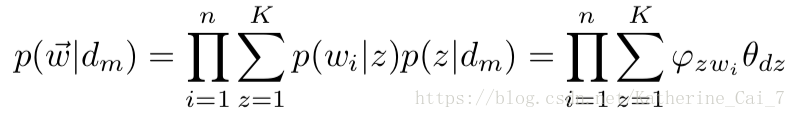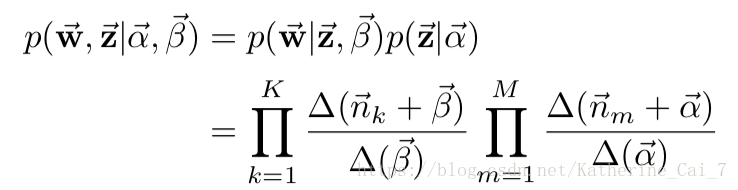LDA是自然语言处理中非常常用的一个主题模型,全称是隐含狄利克雷分布(Latent Dirichlet Allocation),简称LDA。作用是将文档集中每篇文档的主题以概率分布的形式给出,然后通过分析分到同一主题下的文档抽取其实际的主题(模型运行结果就是一个索引编号,通过分析,将这种编号赋予实际的意义,通常的分析方法就是通过分析每个topic下最重要的term来进行总结归纳),根据主题分布进行主题聚类或文本分类。这里需要了解的一个事实是,一篇文档可以包含多个主题,所以会有主题分布这个概率。可以认为文档中的每个词都由其中的一个主题生成。可以这么理解一篇文章的生成:先以一定的概率选取某个主题,然后再以一定的概率选取该主题下的某个词,不断重复这两步,直到完成整个文档。LDA解决的问题就是,分析给定的一篇文章都有什么主题,每个主题出现的占比大小是多少(需要注意的是,为给这个模型的数据是词袋构成的向量,没有考虑词与词的先后关系,对这个问题的改进可以用bi-gram来解决)。p.s.LDA对短文本的主题分类效果比较差。
看过很多LDA相关的模型解释类文档,几乎都是上来先介绍gamma函数,然后4个分布blahblah的一堆很晦涩的数学概念和定义,经常看着一头雾水,没耐心看到最后。这里换个写法,先大致介绍模型整体,然后再去揪那些数学细节。
插个题外话:如果没记错的话,概率论里有两大学派——频度派和贝叶斯派。贝叶斯派的整个的思想过程:先验分布 + 样本信息 => 后验分布。这里涉及到三个概念:先验概率、似然函数和后验概率。其中先验概率是当事情未发生时对事情的判断,可以理解为人类对某些事情认知的固有猜测,很可能是不准的,不符合当时情况的。后验分布就是在经过样本观察后对先验知识的修正后的真实值。而其中的似然函数就是就当于生成函数一样的存在,是先验函数的一个调整函数。贝叶斯学派的思想很像机器学习的一个训练过程,机器学习的权重,或者参数的初始化相当于这里的先验概率,通过样本训练,最终得到真实的后验概率。
回归正题,从宏观上来看,在LDA模型中,以topic作为中间层,问题可以用如下形式进行表示:P(单词|文档) = P(单词|主题) × P(主题|文档),即P(w|d) = P(w|t)×P(t|d),其中的P(单词|文档)是已知的,直接从给定的文档中就可以计算得出的,P(单词|主题)和P(主题|文档)是用来进行拟合的,调整这两个分布,直至符合单词文档的实际分布。也就是说,最终需要求的是P(单词|主题)和P(主题|文档)这两个分布,而真正对文档主题分布有用的,是P(主题|文档)这个分布,即P(t|d)。
下面介绍整个模型的一个标准流程,整个模型可以抽象成以下几个步骤:
1)对于语料库中的每篇文档,从主题分布中抽取一个主题
2)从上述被抽到的主题所对应的单词分布中,抽取一个单词
重复上述过程,直至遍历文档中的每一个单词。
需要反复调整那两个待调分布,比如说,随机先选了一个主题:体育,如果说以体育为主题时对应最终的词频分布和真实文档中的词频分布很像,则体育这个主题对应的P值应该调高一点,否则就低一点,一次往复。对于单词主题的分布也是这么调。
再稍微具体一点:w代表单词,d代表文档,t代表主题;大写代表总集合,小写代表个体
D中每个文档d看做一个单词序列,其中wi表示第i个单词。D中涉及的所有不同单词组成一个词汇表大集合V,LDA以文档集合D作为输入,希望训练出的两个结果向量,即P(单词|主题)和P(主题|文档)这两个概率分布。假设形成k个主题,V中一共有m个词,对每个D中的文档d,对应到不同主题的概率
,其中pti表示d对应T中第i个主题的概率。计算方法是直观的,
,其中nti表示d中对应第i个topic的词的数目,n是d中所有词的总数。对于T中的主题topict,生成不同单词的概率
,其中,pwi表示t生成V中第i个单词的概率。计算方法也很直观,
,其中Nwi表示对应到topict的V中第i个单词的数目,N表示所有对应到topict的单词总数。也就是说,p(t|d)用
计算得到,p(w|t)用
计算得到。
LDA的学习过程如下:
开始时,先随机给和
赋值(对所有的d和t),相当于是先验值。然后:
1.针对一个特定的文档ds中的第i个单词wi,如果令该单词对应的topic为tj,可以把上述公式改写为Pj(wi|ds) = P(wi|tj)*P(tj|ds)
2)枚举T中的topic,得到所有的Pj(wi|ds)。然后可以根据这些概率值结果为ds中的第i个单词wi选择一个topic。最简单的方法是取令Pj(wi|ds)最大的tj(注意,这个式子里只有j是变量)
3)然后,如果ds中的第i个单词wi在这里选择了一个与原先不同的topic(也就是说,这个时候i在遍历ds中所有的单词,而tj理当不变),就会对和
有影响了,它们的影响又会反过来影响对上面提到的P(w|d)的计算。对D中所有的d中的所有w进行一次P(w|d)的计算并重新选择topic看做一次迭代。这样进行n次循环迭代后,就会收敛到LDA所需要的结果了
***********************************************************华丽丽的分界线***********************************************************
上面是整个LDA的大体流程以及具体解决问题的思路。下面进入尿点时刻,开始进行数学推导(就是gamma函数那一堆乱码七糟的玩意儿)。
先介绍几个概念:
1.共轭分布和共轭先验:前边说贝叶斯派中,后验概率 ∝ 先验概率 × 似然函数。如果说,先验概率和后验概率在形式上是相同的,那么就可以说二者是概率共轭的关系。比如说:
先验概率为:
后验概率为:
这两个概率形式形式一致,只有参数不同,则这二者是概率共轭的关系,其中前者为后者的共轭先验函数。为啥要有共轭这么个东西呢?是为了计算的简便,概率的形式定了,只需要调参,所以会极大简化运算量。
2.gamma函数:这个函数本质上就是阶乘函数在实数上的推广。
对于整数而言,阶乘函数:,形式如1×2×3×4×...n-1
对于实数而言,不能用上述公式进行计算,阶乘函数为:
3.二项分布:对于结果的取值只有两种情况,可以认为这两种情况就是0-1。其中取值为0的概率为p,取值为1的概率为1-p。那么对于n次独立实验来说,
p.s.只做一次实验,是伯努利分布;重复做n次,就是二项分布。
4.多项分布:把二项分布扩展到多维的情况,也就是说对结果的取值不是只有两种,而是有n多种可能的取值。
5.Beta分布:二项分布的共轭先验分布,其形式和二项分布特别像。
6.狄利克雷分布:Beta分布在高维上的扩展。
几个主题模型:
1.unigram:这个是最简单的主题模型,可是最粗糙,效果最烂的主题模型,效果和模型复杂度远远小于LDA。
思想如下:对于文档w = ,这里做了一个假设,一个单词出现的概率只和其自身有关,用
表示词wn的先验概率,即这个单词可能出现的概率。这个模型可以理解为是掷一个骰子,这个骰子有V个面,每个面对应一个词,各个面的概率不一样。那么一个由N个单词组成的文档就相当于是独立地掷了N次骰子,满足多项分布。用数学公式的方式表示为
。也就是说,用本身来观测本身,这种模型时最弱鸡的。
2.mixture of unigram models:unigram模型的升级版。给某个文档先选择一个主题z,再根据该主题生成文档, 该文档中的所有词都来自一个主题,也就是说引入了一个topic变量,相当于是说有很多个骰子,骰子的个数就是topic的数量。最后算出生成文档的概率。整个过程就变成了,先随机选一个骰子,然后独立掷N次这个骰子产生N个单词,组成整个文档。这里一个文章只有一个主题。
3.pLSA:前边的模型其实是不符合人类正常的文档构思的,也就是说,正常人写一个文档,这个文档很可能会属于多个主题,而不是一个主题,各个主题的占比会不一样。每个topic都是词汇上的概率分布,文章中的每个词都是由一个固定的topic生成的。举个例子如下:
这里还是拿骰子来进行说明,有两个骰子:topic骰子和word骰子。一共有K个topic骰子,每个topic都有一个对应的word骰子,每个word骰子有V个面。那么整个文档的生成过程就是先投掷topic骰子,得到topici,然后投掷topici对应的word骰子,得到单词。则整篇文档的生成概率为:
模型中的参数求解可以用EM算法来进行求解。
4.LDA:就是将pLSA的基础上加了层贝叶斯框架,即LDA就是pLSA的贝叶斯版本。这个贝叶斯框架就体现在狄利克雷先验分布上。
在前边的pLSA模型中,没用什么先验分布,直接认为是个随机过程。这贝叶斯派那帮人简直不能忍啊,这不科学啊,应该有先验分布的啊,不能不按套路啊,所以这帮人就在那两个骰子参数上加上个先验分布,把这个pLSA改造成一个贝叶斯过程。这里用到的先验分布就是狄利克雷分布。根据前边说的文档的生成过程,现在可以把文档的生成抽象成如下几个问题:
1)从狄利克雷分布α中抽样,生成文档d的主题分布θ
2)从主题的多项式分布θ中抽样,生成文档d的第i个词的主题zi
3)从狄利克雷分布β中抽样,生成主题zi对应的词语分布φi
4)从词语的多项式分布φi中采样,最终生成词语wi
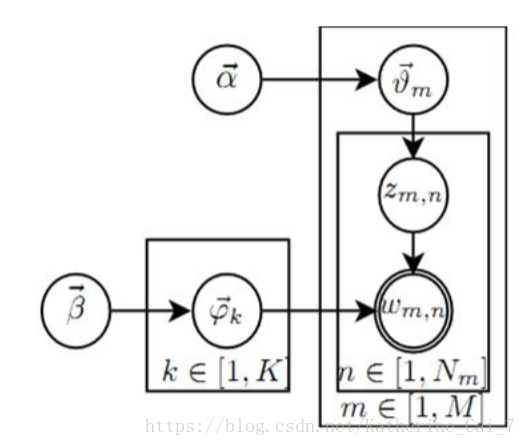
这里一共涉及到4个分布,为啥要用狄利克雷分布呢?这个分布存在的意义在于约束不确定的变量值应该在哪个区间变化,最后得出的参数别太离谱。这个狄利克雷分布是一个指数族分布,是多项分布的共轭先验,这些性质保证了学习的便利。LDA的过程可以用如下图来进行表示:
这个模型图的解释如下:
1.:这个过程表示生成第n个词对应的topic。在生成第m篇文档的时候,先从topic骰子中抽了一个骰子
,然后投掷这个骰子,得到文档中第n个词的topic编号
2.:这个过程表示生成文档中的第n个词。在手里的K个word骰子中,选编号为
的那个骰子进行投掷,生成
这里需要提一下狄利克雷分布的问题:对于一个3维狄利克雷参数向量(α, α, α)来说,当α小于1时,生成的概率向量偏向于某几维,值越小,偏得越厉害;当α大于1时,生成的概率向量倾向于中间,值越大,趋中越厉害。
经过一堆的数学推导之后,最后的形式是这个样子的:
其中的α和β就是狄利克雷分布的两个参数,K是语料中的topic数,是个超参,M是语料集中的文档数,,其中
表示第k个topic产生的词中word t的个数。
得到了p(w,z)这个干净的表达式之后,就可以用gibbs sampling算法对这个分布进行采样。为什么要进行采样呢?当我们在面对一个未知或者复杂的分布时,积分、期望或者说联合分布很难算出来,是个NP难问题,但是条件概率很容易算出来,这时候就要进行采样。采样的目的是得到这个分布的样本,通过这些样本明确出该分布的具体结构,常用MCMC来进行分布采样。MCMC本身解决的是无法直接采样或理解的分布问题的,不是对已知分布进行采样。gibbs是对MCMC的一种改进。在LDA中,后验概率无法直接获得,我们通过gibbs采样的方法去采样该分布,从而得到模型结构。
我们现在需要求的是p(z|w),需要采样的也是p(z|w)这个分布,就是求某个单词应该属于什么topic。gibbs采样采的是(w, z),即联合分布的样本。收敛后在联合分布的样本空间,统计出各个参数。LDA是个生成模型,但是直接求联合分布概率,分母计算量比较大,只能通过gibbs采样,采样出联合分布的样本,执行多次之后产生的样本服从真实样本的分布,然后在联合样本空间计算出统计特性。gibbs采样做LDA的好处是简单,速度快,收敛结果也不错。
以上就是整个LDA的大致过程,通俗版以及公式版。简而言之,pLSA贝叶斯化就变成了LDA,对LDA模型进行改进有很多种方式,LDA的非参数化就变成了HDP(这个模型的优点就是自动确定topic的个数)