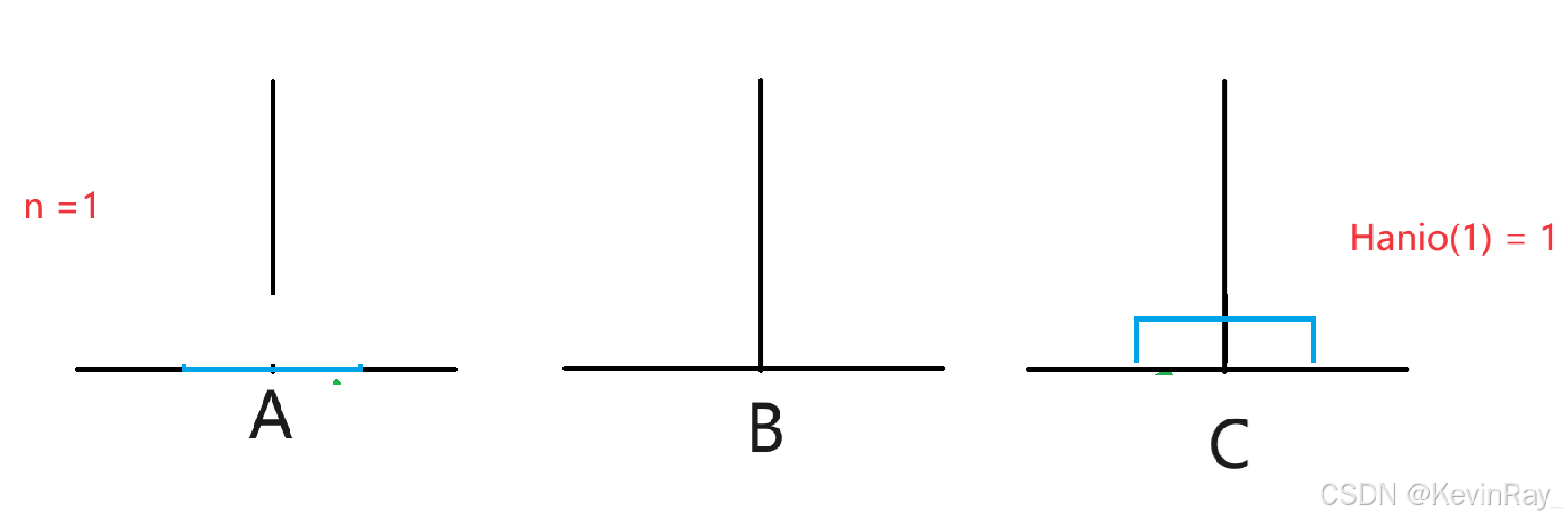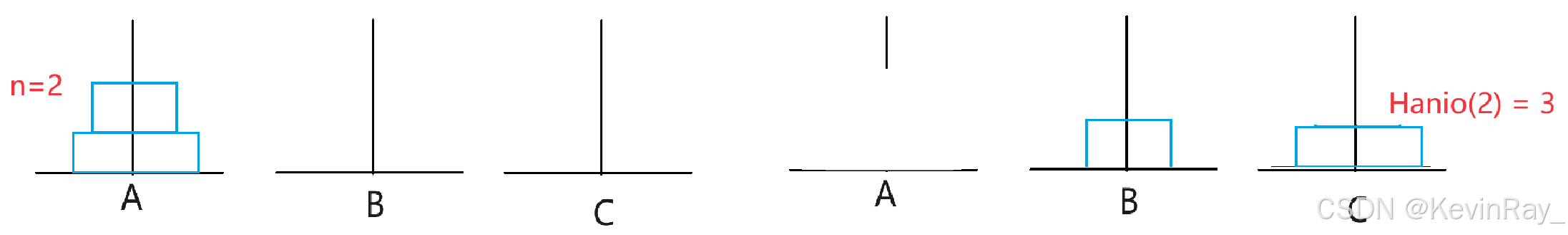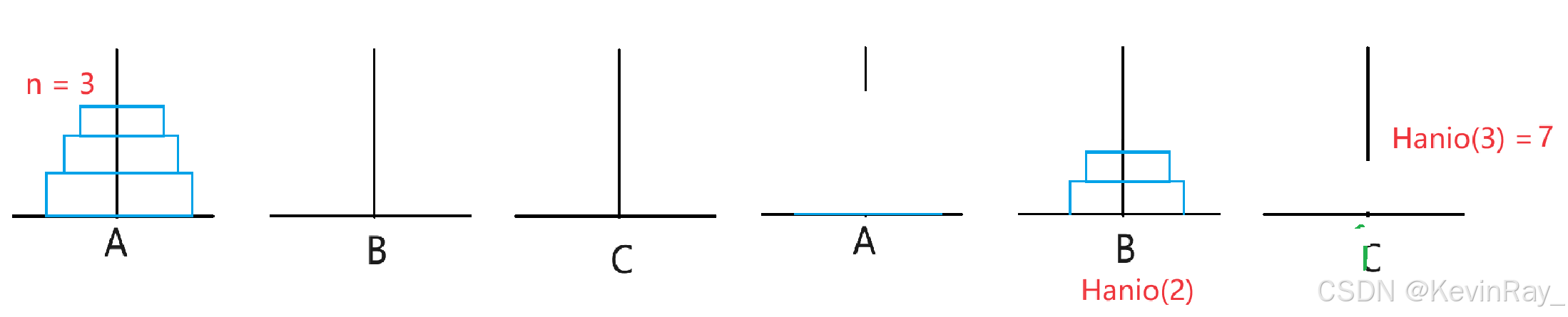前言
递归广泛应用于计算机科学中的许多领域,例如数学,排序算法,树和图的遍历等。在实际编程中,递归可以帮助简化问题的解决方案,使代码更简洁和可读。
一、递归的概念
递归是一种算法或函数的编程技巧,它允许函数在其定义中调用自身。
递归中的递就是递推的意思,归就是回归的意思。
1. 递归举例
例如:
#include <stdio.h>
int main()
{
printf("hehe\n");
main();//main函数中⼜调⽤了main函数
return 0;
}上述就是⼀个简单的递归程序,只不过上⾯的递归只是为了演⽰递归的基本形式,不是为了解决问 题,代码最终也会陷⼊死递归,导致栈溢出(Stack overflow)。
栈溢出指的是当一个程序在执行过程中,向栈空间中写入的数据超过了栈的容量限制,导致覆盖了其他变量或重要数据的情况。这通常是由于递归函数调用过深、局部变量过多等原因引起的。栈溢出可能导致程序崩溃、异常或者安全漏洞。
2. 递归的思想
把⼀个⼤型复杂问题层层转化为⼀个与原问题相似,但规模较⼩的⼦问题来求解;直到⼦问题不能再 被拆分,递归就结束了。所以递归的思考⽅式就是把⼤事化⼩的过程。
3. 递归的关键
递归通常用于解决需要重复执行相同或相似任务的问题,其中每个任务的解决方案取决于更简单版本的相同任务。
递归的关键是找到基本情况和递归情况。
- 基本情况是问题的最简单形式,通常是没有更多递归调用的情况。在基本情况下,递归函数直接返回结果。
- 递归情况是问题的一般情况,其中递归函数调用自身以解决更简单的子问题,并将这些子问题的结果组合成原始问题的解决方案。
二、递归的理解
递归的限制条件
递归需要函数调用自身,所以必须要有一定的限制条件,让函数的调用在某种条件下停下来,这里所说的某种条件也就是基本情况。
-
结束条件:为了避免无限递归,必须保证在一定条件下递归终止。这通常是在基本情况下,即不能再进一步使用递归解决问题的情况。
-
问题的规模缩小:递归函数必须能够将原始问题拆分成更小的子问题,以便递归调用可以解决。否则,递归将无法完成,并可能导致无限递归。这里所说的规模缩小也就是递归需要不断逼近约束条件,直至约束条件开始返回,才可以解决问题。
那么具体如何理解呢?让我们从下面的例子中去慢慢理解,相信你在学习完下面的例子之后会对递归有一定的理解。
三、递归与数学模型
进入这部分之后我们开始考虑如何解决问题,这里容我定义两个概念方便之后的理解。
我们将上面的第一条结束条件定义为基本条件,也就是说什么时候递归停止;将问题规模缩小定义为逼近条件,非常形象,也就是说怎么逼近基本条件。在实际解决问题时我们需要先从基本条件入手开始考虑。
为了更好的理解递归我将引入两个模型有助于更好的学习递归:一个是这个部分的数学模型,一个是下部分的生活模型,我会从这两个模型出发,带大家理解递归,并帮助你写出递归。
1. 递归与数列
看到小标题,你应该知道了,这里我引入数列帮助你理解递归,我认为数列在解决数学类问题上和递归思想是高度重合的,即使你没学过数列也不要紧,我们只引入简单的递推数列。
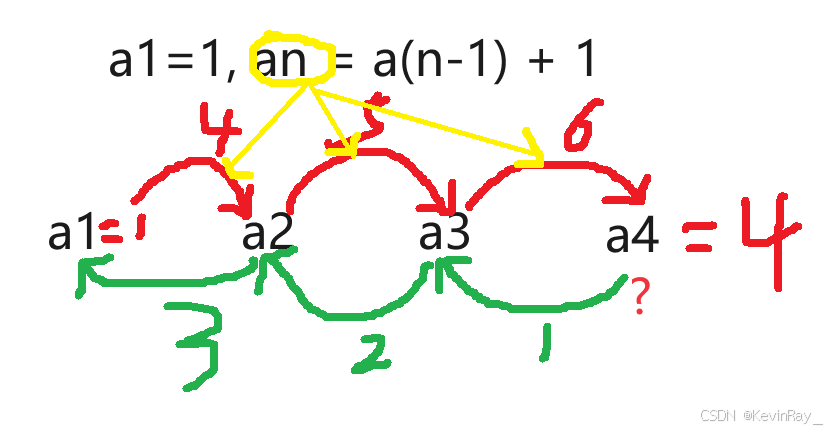
下面是一个简单的递推数列,首项为1,前项与后项之间差1:
根据递推的概念,首项为1就是基本条件,那么后项等于前项加1就是基本条件。想想,假设我们要求第4项,也就是
,那么我们只需要知道
再加1就好;但是
我们也不知道,那么我们需要
;
我们也不知道,那么我们需要知道
;很好,我们知道
是1,然后我们只需要倒着往上计算,一次一次加就可以知道第4项为4。
如果你明白这个,那么很好,你已经懂递归了。
我们回过来看一下,首先,我们知道了首项也就是基本条件,在后面的推导中,我们知道它非常重要,没有它递归永远也停不下来;其次,我们需要一个递推条件,也可以说是递推式,也就是递归里的逼近条件,有了这个条件,我们可以不断往回去找,直到找到我们的已知条件;最后,我们开始返回,带着已知条件,在往后走,返回我们需要的第某项的值。
经过这三步,我们就可以完成一次递归了,可以发现,递归需要先倒着往回找,然后再正着返回,这意味这它需要很多的空间,所以也容易造成栈溢出。那么,理解了简单的递归,我们做几个题练练手。
2. 利用递归解决数学类问题
题目1:求n的阶乘
⼀个正整数的阶乘(factorial)是所有⼩于及等于该数的正整数的积,并且0的阶乘为1。⾃然数n的阶乘写作n!。计算n的阶乘(不考虑溢出),n的阶乘就是1~n的数字累积相乘。
2.1.1 分析与代码实现
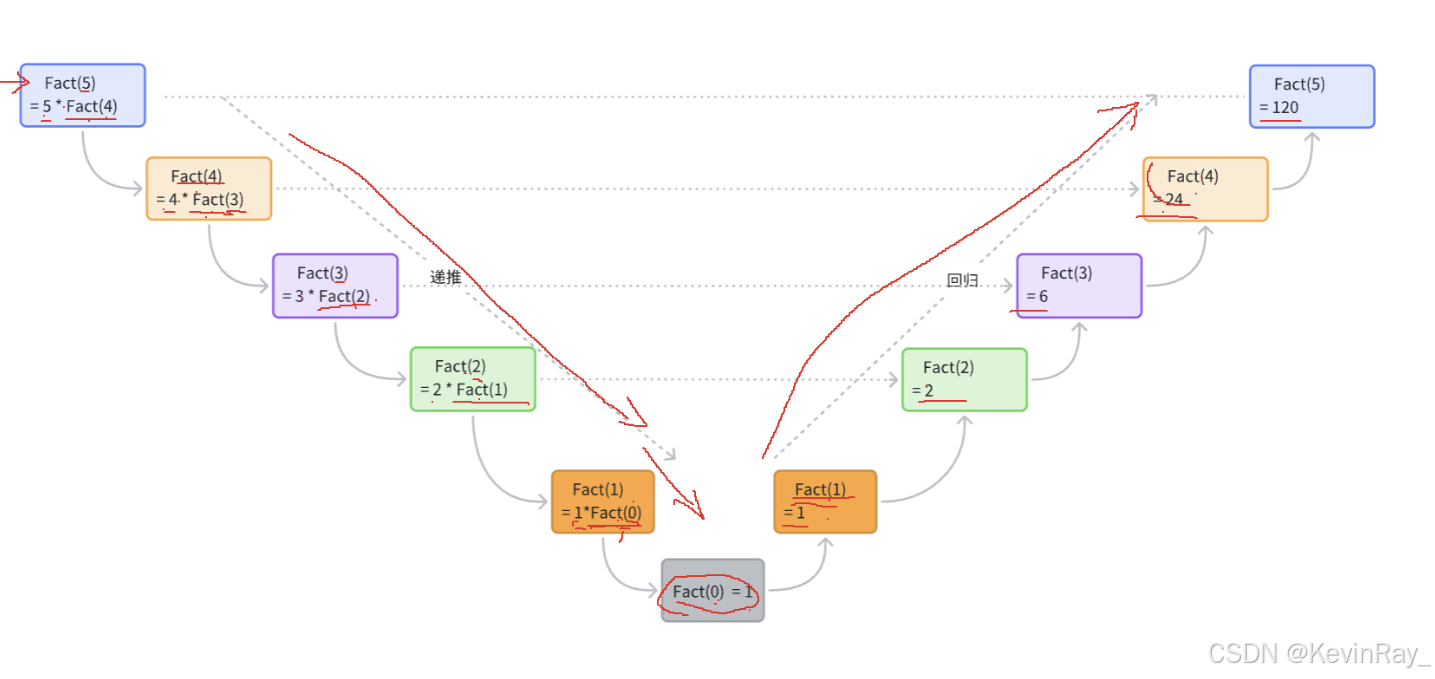
我们知道n的阶乘的公式:n! = n ∗ (n − 1)!
举例:
5! = 5*4*3*2*1
4! = 4*3*2*1
所以:5! = 5*4!
基本条件:n=0时,0!= 1;
逼近条件:n! = n ∗ (n − 1)!
代码实现:
int Fact(int n)
{
if(n==0)
return 1;
else
return n*Fact(n-1);
}
2.1.2 画图推演
题目2:求第n个斐波那契数
斐波那契数列是指这样一个数列:1,1,2,3,5,8,13,21,34,55,89……这个数列从第3项开始 ,每一项都等于前两项之和。
2.2.1 分析与代码实现
基本条件:Fib(0) =1;Fib(1) =1
逼近条件:Fib(n) = Fib(n-1) + Fib(n-2)
代码实现:
int Fib(int n)
{
if (n <= 2)
{
return 1;
}
else
{
return Fib(n - 1) + Fib(n - 2);
}
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret = Fib(n);
printf("%d\n", ret);
return 0;
}2.2.2 运行结果
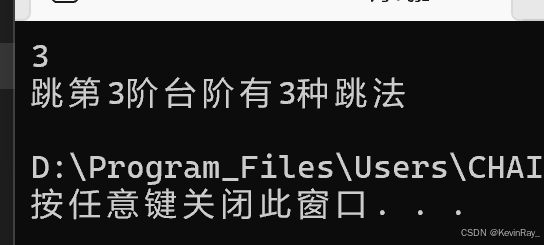
题目3:青蛙跳台阶问题
一只青蛙一次最少可以跳 1层 台阶,一次最多可以跳 2层 台阶,求:该青蛙跳上n 层 的台阶总共有多少种跳法
2.3.1 分析与代码实现
青蛙跳台阶问题事实上也是一个斐波那契数列问题。
1个台阶 1种跳法
2个台阶 2种跳法
3个台阶 3种跳法
4个台阶 5种跳法
5个台阶 8种跳法
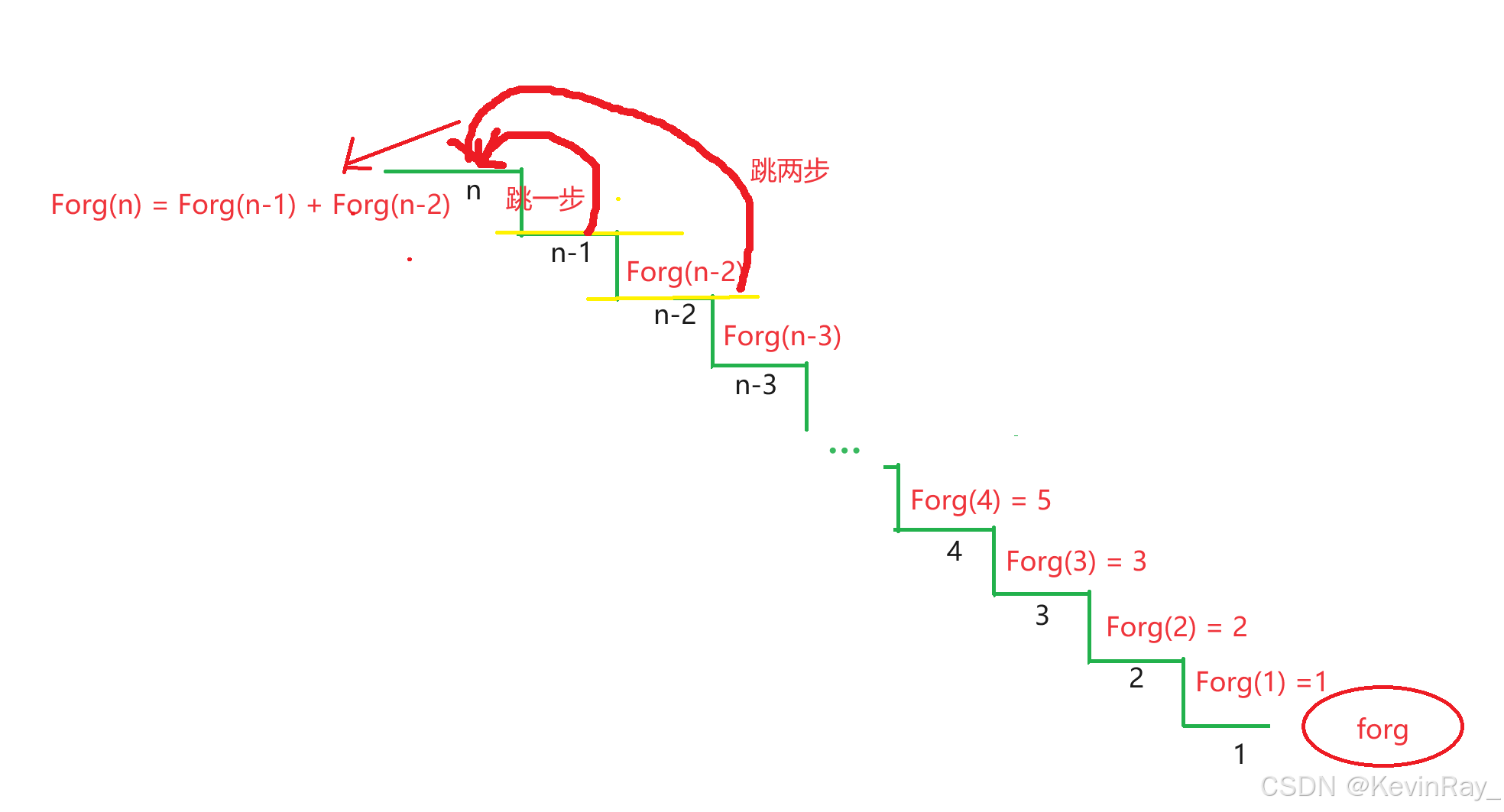
当前台阶数下的跳法等于前两台阶数的跳法数之和,这是由于当青蛙想跳上第n层的台阶时,它必须先跳到第n-1阶或者第n-2阶,然后才能在跳一步或两步跳到第n阶。同样的要是它想跳到第n-1阶,它需要先跳到第n-2阶或者第n-3阶,这样就形成了一个递归。
基本条件:Forg(1) = 1, Forg(2) = 2
逼近条件:Forg(n) = Forg(n-1) + Forg(n-2)
图示如下:
代码实现:
int Forg(int n)
{
if (n == 1)
{
return 1;
}
else if (n == 2)
{
return 2;
}
else
{
return Forg(n - 1) + Forg(n - 2);
}
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret = Forg(n);
printf("跳第%d阶台阶有%d种跳法\n", n, ret);
return 0;
}2.3.2 运行结果
四、递归与生活模型
学完了数学模型,这类问题的特点是你可以很容易的用具体的递推式将他们表达出来,但是要解决具体生活中的问题这显然不现实,不是所有的生活中的问题都可以用数学公式来表达。
我们需要对他们进行抽象,再用生活化模型去去表达。
1.递归与冰箱装大象问题
世纪之交那年的春晚,在一个叫做《钟点工》的小品中,宋丹丹老师告诉全国观众把大象放进冰箱拢共需要三步:
第一步:把冰箱门打开;
第二步:把大象放进去;
第三步:把冰箱门带上。
这看上去似乎很荒谬,但是我们忽略细小的步骤来看确实是这样。没有知道把大象放进冰箱的过程中还需要多少步,但是我们对它进行抽象,只看重点,也可以这样来理解。
假设我们要把这个问题写成一个递归,那么我们需要关注什么呢?
我们要完成第三步,肯定要完成第二步,我们现在不关心第二步之前还有什么,也不关心第二步内部具体需要做什么,我们只关注第二步的结果传递过来,那么我们就可以做第三步了。
假设我们有这样Elephant()可以实现这个功能,那么我们可以这样表示:
Elephant(3) = Elephant(2) + 第三步
但是我们并不知道第二步需要什么,所以我们需要知道前一步,也就是第一步,我们清楚只要第一步做完了,然后把结果传过来我们就可以做第二步了。好的,那么同样的:
Elephant(2) = Elephant(2) + 第二步
很完美,现在我们知道第一步是要打开冰箱门了,那么再做第二步、第三步就可以完美的完成这个函数!!!
这个函数当然无法运行,但是我们表达一下这个思想,它可以将生活中的问题转化为一个递归,这个思想是没问题的。
void Elephant(int n)
{
if(n == 1)
{
把冰箱门打开;
}
else if(n ==2){
Elephant(1) + 把大象放进去;
}
else
{
Elephant(2) + 把冰箱门带上;
}
}
2. 利用递归解决生活类问题
题目1其实也是一个数学类问题,但是我觉得这里用生活类的理解更方便。
题目1:顺序打印⼀个整数的每⼀位
输⼊⼀个整数m,按照顺序打印整数的每⼀位。
⽐如:
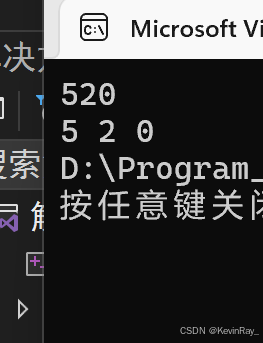
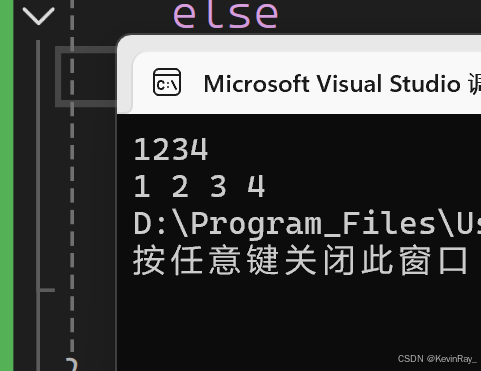
输⼊:1234 输出:1 2 3 4
输⼊:520 输出:5 2 0
2.1.1 分析与代码实现
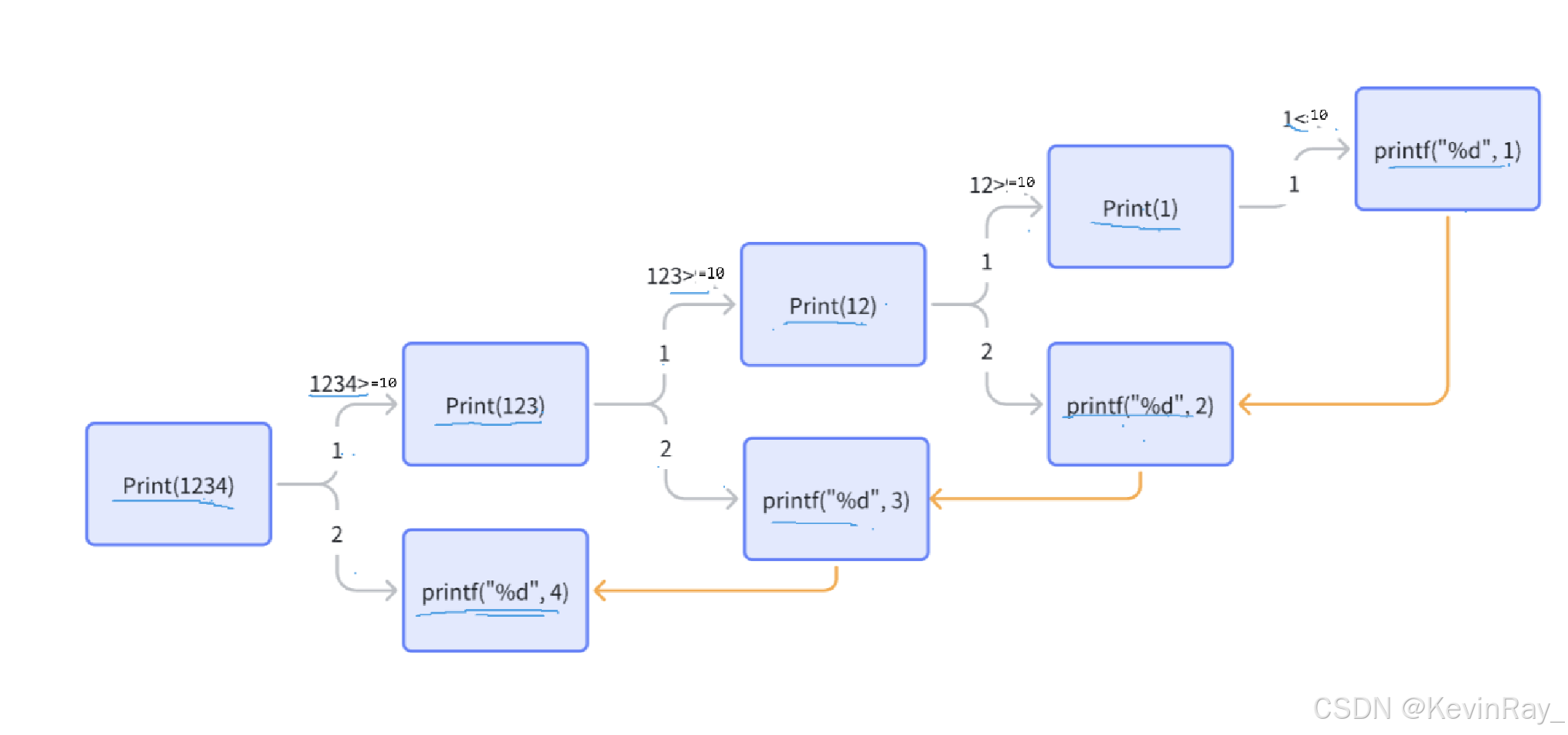
打印的数据不同主要是数位多少的差别,如果只有一位数,就可以直接打印;如果是两位数,那么需要先打印打印先一位,再打印个位数;如果是n位数呢?需要先一直寻找到只剩一位,再一直返回加一位,直到n位。
我们不必关心之前的有多少位数,我们只关心,如果要打印所有数字就必须先打印第一位数字,第一位数字被打印以后,才开始打印后面的数字;要打印剩下的n-1位数,又需要打印第一位数,依次类推。
基本条件:Print(只有一位数) = 一位数本身
逼近条件:Print(n位数) = Print(后n-1位) + Print(第一位)
代码实现:
#include <stdio.h>
void Print(int n)
{
if (n < 10)
{
printf("%d ", n);
}
else
{
Print(n / 10);
Print(n % 10);
}
}
int main()
{
int n = 0;
scanf("%d", &n);
Print(n);
return 0;
}2.1.2 运行结果
2.1.3 画图推演
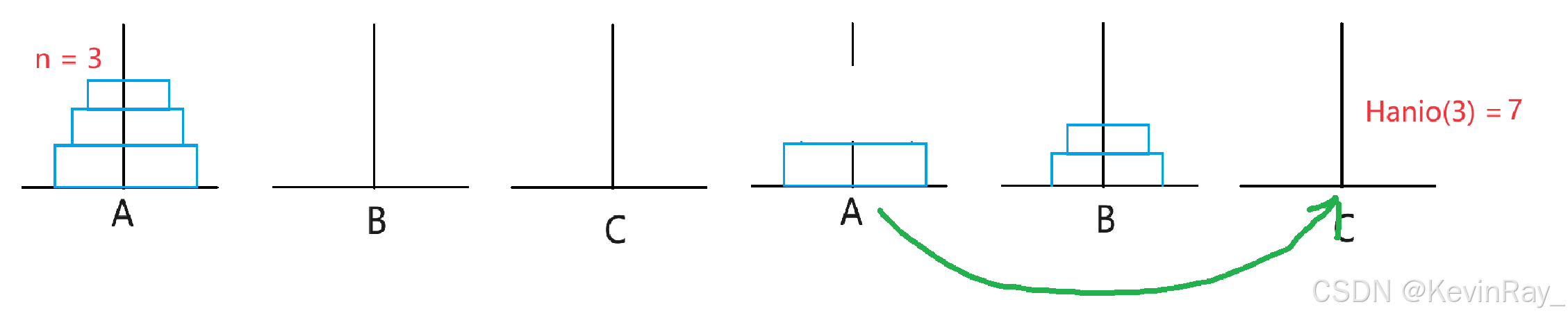
题目2:汉诺塔问题
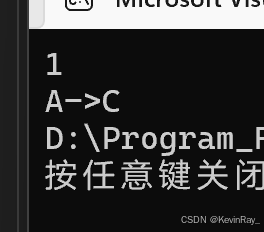
给定三根柱子,记为 𝐴,𝐵,𝐶 ,其中 𝐴 柱子上有 𝑛 个盘子,从上到下编号为 0 到 𝑛−1 ,且上面的盘子一定比下面的盘子小。问:将 𝐴 柱上的盘子经由 𝐵 柱移动到 𝐶 柱最少需要多少次?
移动时应注意:① 一次只能移动一个盘子
②大的盘子不能压在小盘子上
2.2.1 分析与代码实现
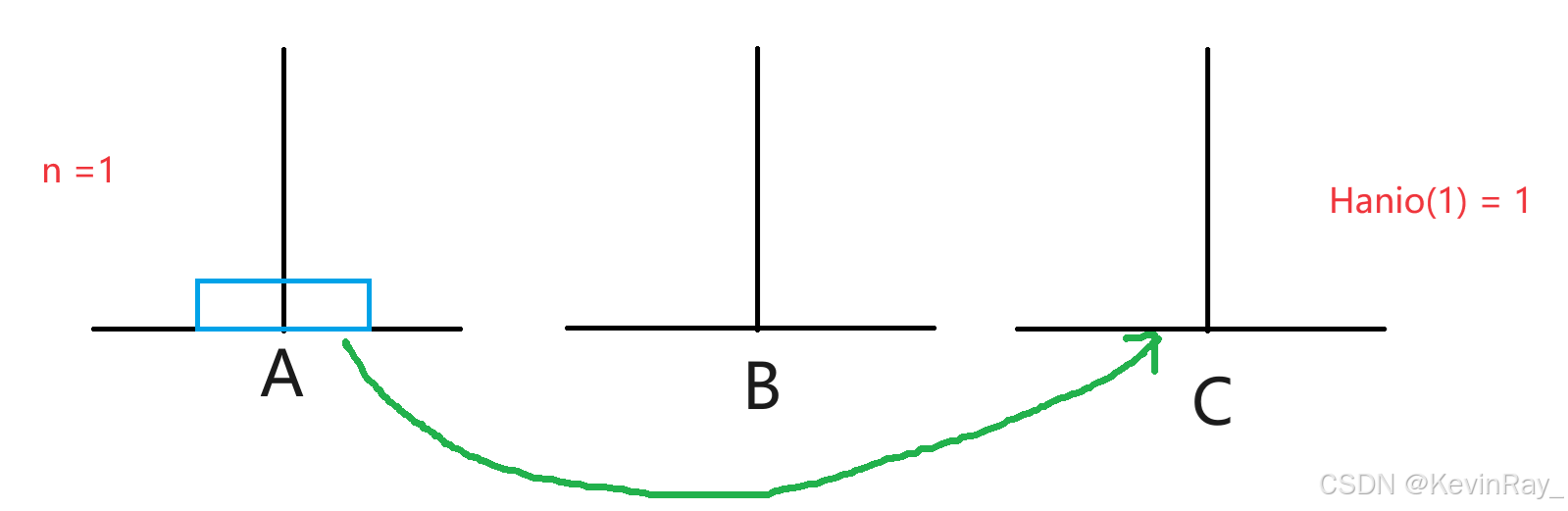
当n = 1时:
只有一步:A->C
当n = 2时:
有三步:A->B, A->C, B->C
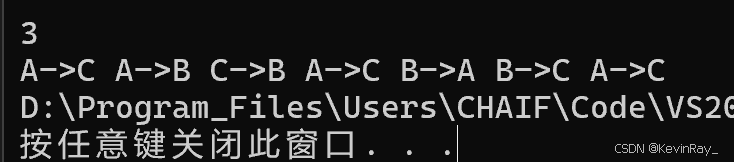
当n = 3时:
有七步:A->C, A->B, C->B, A->C, B->A, B->C, A->C
在移动过程过,似乎很难找到什么规律,但是我们可以发现不管有几个盘子,总有一次移动会呈现如右图这个情况。似乎这一步还是没有什么规律,我们不知道它之前需要移多少步,也不知道它之后移多少步。但是,我们继续进行下一步呢?
现在我们发现:
n=1时,下一步就是最后一步;
n = 2时,现在最大的盘子已经到了目标C柱,C柱其实可以等价为一个空柱了。因为现在任意一个盘子都可以移动到该柱子上,之后操作没有任何影响,那么现在这种情况跟n=1时好像没太大区别,唯一的区别就是n=1情况下,A柱上只有一个盘子,而现在的一个盘子在B柱上;
n = 3时,同样的C柱也可以等价为一个空柱了,现在任意一个盘子都可以移动到该柱子上,对之后操作没有任何影响,那么现在这种情况跟n=2也没太大区别,唯一的区别就是n=2情况下,A柱上有两个盘子,而现在的两个盘子在B柱上;
抽象如下图:
到这里,你应该已经有所发现了。
现在我们不关心别的,只需要像把大象装进冰箱一样做三件事:
1. 打开冰箱门 —— 把n-1个盘子移到B上,A上只剩一个最大的
2. 把大象放进冰箱 —— 把最大的盘子移动到C上,继续让n-1个盘子执行Hanio(n-1)
3. 关上冰箱门 —— 直到执行到Hanio(1), 将最后一个盘子移到C上去
基本条件:n =1时,Hanio(1) = 1
逼近条件:
Hanio(n) = Hanio(n-1)(以A为起始杆,B为终止杆,将n-1个盘子移到B上) + (A->C)+ Hanio(n-1)(以B为起始杆,C为目标杆,将n-1个盘子移到C上)
代码实现:
void Move(char begin, char end)
{
printf("%c->%c ", begin, end);
}
void Hanio(int n, char begin, char tmp, char end)
{
if (n == 1)
{
Move(begin, end);
}
else
{
Hanio(n - 1, begin, end, tmp);
Move(begin, end);
Hanio(n - 1, tmp, begin, end);
}
}
int main()
{
int n = 0;
scanf("%d", &n);
Hanio(n, 'A', 'B', 'C');
return 0;
}2.2.2 运行结果
总结
递归的核心是定义递归函数和停止条件。递归函数将问题分解为更小的子问题,然后通过调用自身解决这些子问题。停止条件是指当达到一定条件时,递归函数不再调用自身,从而避免无限递归。
使用递归的优势之一是简化问题的复杂度。通过将问题分解为更小的子问题,可以减少问题的规模,从而使得解决问题变得更加容易和直观。此外,递归也能够提高代码的可读性和可维护性,因为它可以更好地表达问题的本质和逻辑结构。
然而,递归也有一些限制和注意事项。首先,递归可能会导致性能问题,特别是当递归深度过大时。其次,递归可能会消耗大量的堆栈空间,因为每次递归调用都会在堆栈中创建一个新的函数帧。此外,递归还可能存在无限递归的风险,如果没有正确地定义停止条件,递归函数可能会无限循环。
总的来说,递归是一种强大而有用的解决问题的方法。通过将复杂问题分解为更小的子问题,递归能够简化问题的复杂度,提高代码的可读性和可维护性。但是,使用递归时需要注意性能和内存的消耗,并确保正确地定义停止条件,以避免无限递归的问题。