了解VGGNet卷积网络模型

2014年ILSVRC图像分类竞赛的第二名就是VGGNet网络模型。我们为什么要研究第二名的模型？因为在讲网络迁移到其他图片数据上进行应用时，VGGNet比第一名的GoogleNet有着更好的泛化性，尽管它有很多缺陷。
那么VGG网络长啥样呢？我们还是老规矩，先上一波图再说！

模型结构

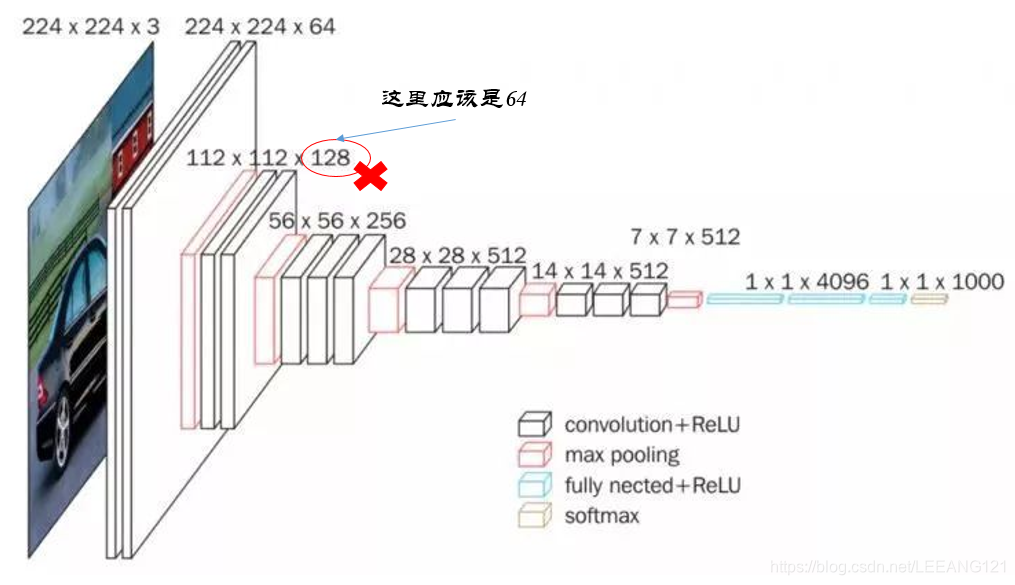
上面两幅图就是关于VGG网络结构的一个传播过程，详细解释如下：
观察图片得知，我们一共使用了5层卷积。具体分析如下：
第一层卷积

1，首先我们输入一副图片，这个图片的像素尺寸是224x224，由于是彩色图片，有3个通道，因此实际输入尺寸为224x224x3

2，我们引入卷积核，卷积核的大小为3x3，根据我们对卷积核的了解，由于输入是一个3通道的张量，因此卷积核的深度也是3.所以卷积核的实际尺寸为3x3x3

3，根据图例，我们的第一层卷积为22422464，这个大小是如何得到的？

根据问题2，我们知道我们引入的卷积核尺寸为3x3，根据上面的表，我们知道步长为1，此时卷积后得到的张量维度应该为（224-3+1）/1=222，因此不难推测，我们对原始输入模型增加了padding：（224-3+1+2）/1=224. 我们知道，通过3x3x3的卷积核对原始输入进行卷积后得到的张量深度为1，因此，我们采用了64个这样的卷积核，最后得到了深度为64的张量。

4，我们引入2x2的最大池化层，缩小数组的维度，由224x224x64变为112x112x64（注意，池化层紧紧是缩小模型的长和宽，不会改变模型的深度，因此这里深度依然为64，而非128）

第二层卷积

1，现在我们的输入从原始图像变成了由第一层卷积之后的输出数组：112x112x64. 我们再次引入和之前相同尺寸的卷积核，但是深度由原来的3变成了64（3x3x64），并且引入了128个这个卷积核，因此经过这一轮卷积运算，数组变成了112x112x128.

2，我们引入2x2的池化层，将数组降维变成56x56x128的数组

第三层卷积
1，根据上面的思想，我们现在的输入是56x56x128的数组，我们引入尺寸为3x3x128的卷积核，并且引用了256个，此时数组的大小变为56x56x256

2，我们依然引入2x2的池化层，模型降维成28x28x256

第四层卷积

1，我们按照上面的思路，首先把模型变为28x28x512的数组

2，通过池化层，将模型降维变成14x14x512的数组

第五层卷积
1，我们引入3x3x512的卷积核，但是不改变输入模型的深度，这句话的意思是这种卷积核我们引入512个。

2，通过2x2的池化操作，我们将模型降维变成7x7x512

全连接层
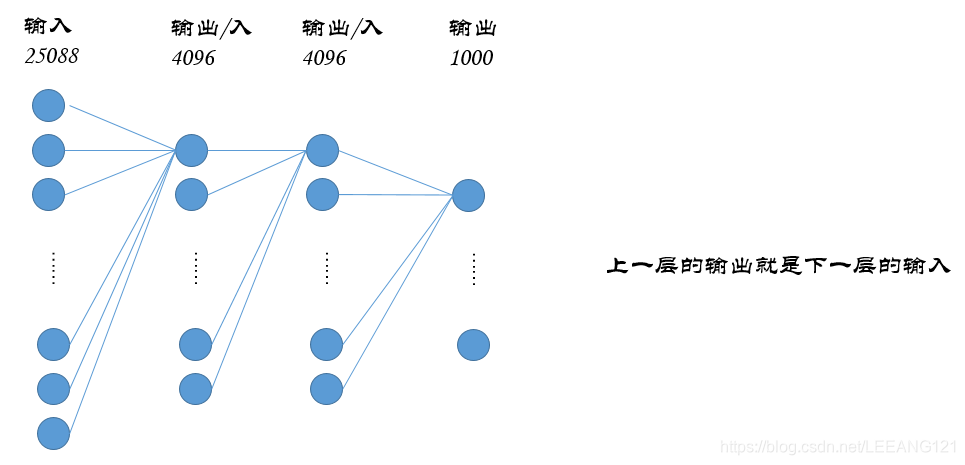
这里要注意一下，我们引入了全连接层，那么对于全连接层而言，输入不再是一个7x7x512的矩阵，现在输入可以想象为一个25088的向量（这个25088就是7x7x512的结果），整个全连接层如下图所示：

以上就是VGG16网络的结构。

关于这个网络模型的一些思考

关于这个网络模型，网上也有很多讲解，但是有些讲述，可能不够细致，大家不易于理解，这里我抛砖引玉，对其中的一些概念做一些补充：

1，为什么使用2个3x3的卷积核代替一个5x5的卷积核？
首先很明显，2个3x3的卷积核包含的参数数量为18个（2x3x3），而一个5x5的卷积核包含的参数数量为25个。所以可以有效降低参数数量。

2，那么问题来了，2个3x3的卷积核可以替代一个5x5的卷积核吗？
当然可以，我们举一个最简单的栗子：
假设我们卷积核的步长为1，padding为0，输入的图形高度为n，那么我们用5x5的卷积核做一轮卷积运算，得到的图形高度为$（（n-5+1）/1=n-4）$
现在我们用3x3的卷积核对这个相同的输入进行卷积运算：1，第一次卷积得到的高度为$（（n-3+1）/1=n-2）$，现在我们对这个结果再进行一次卷积运算，卷积核依然为3x3，此时得到的卷积高度为：$（（n-2-3+1）/1=n-4）$ 显然，两次卷积结果是一样的。完美

3，为什么有时候会使用1x1的卷积核？
为了在输入和输出通道数不改变（不发生降维）的情况下实现线性变换。

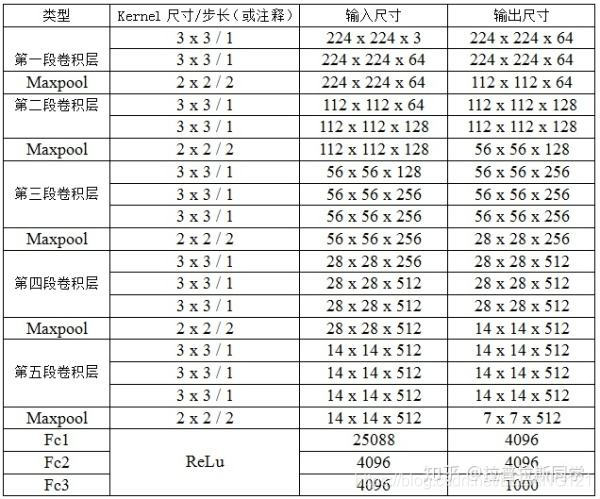
4，最后附上VGGNet各级别的网络结构表

本文仅为帮助初学者了解VGG网络的工作原理，文章写作较为仓促，若有不对的地方，欢迎大家指正。