问题  

近日，一位朋友拿着两个模型预测效果比较的结果来咨询，当然是遇到了一个好像不太正常的现象才来咨询的。两个模型都是二分类结局的，应用常见的Logistic回归模型得到结果如下：模型A的正确率为85%，AUC为0.98；模型B的正确率为93%，AUC为0.92。那么选择哪个模型呢？

很多朋友首先应该会质疑方法使用的正确性，不过出现这个问题的可能性很小，我们假设方法是正确的，主要探讨AUC和正确率矛盾的问题。

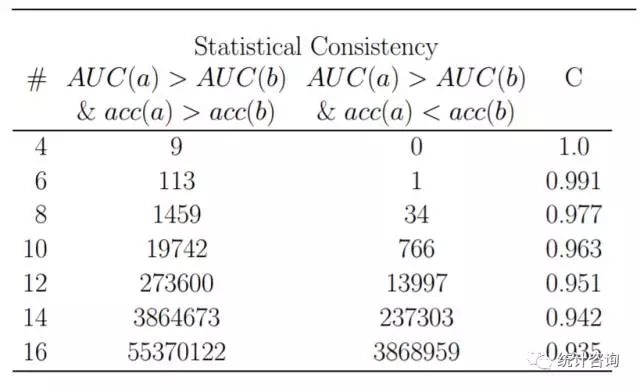
查阅文献，发现不少朋友也遇到同样的问题，更巧的是已有学者通过模拟研究证实矛盾的存在。下面图表中的最后一列展示的正是AUC和正确率结论的一致比例，较低可达93.5%。

解释  

接着我们从简单的理论出发解释一下，两者出现矛盾的可能原因。正确率是基于较佳的截断值计算的，所以很多朋友觉得他应该可靠。但是他们可能不知道，AUC是基于所有可能的截断值计算的，他应该更加稳健。

怎么理解“稳健”这个词呢？我们可以理解为计算正确率时所基于的较佳截断值并不是总体分布中的较佳截断值，正确率只是某个随机样本的一个属性指标。而AUC不关注某个截断值的表现如何，可以综合所有截断值的预测性能，所以正确率高，AUC不一定大，反之亦然。

“The implicit goal of AUC is to deal with situations where you have a skewed sample distribution, and don't want to over-fit to a single class.”，这是文献中的一句话，他想表达的是AUC在偏态的样本中更稳健。比如，一份偏态的样本，包含九十九个0和一个1，如果我们瞎预测全都是0，也有99%的正确率。但是没有考虑到此时的特异度为0。

所以，回到文章开头那位朋友提出的问题，“模型A的正确率为85%，AUC为0.98；模型B的正确率为93%，AUC为0.92”，我们应该根据AUC较大的原则选择模型A作为较佳模型进行后续的分析。

结论  

在模型比较的问题上，正确率和AUC之间，应该选择AUC。引用参考文献中的两点结论：

AUC is a better measure than accuracy based on formal definitions of discriminancy and consistency

The paper recommends using AUC as a “single number” measure to over accuracy when evaluating and comparing classifiers

reportROC包  

最后给大家介绍一个R程序包，一行代码可以轻松输出多个诊断试验评价指标，包括截断值、灵敏度、特异度、AUC、阳性似然比、阴性似然比、阳性预测值、阴性预测值等，最重要的是可以获得上述各个指标的置信区间(据说很多朋友不知道怎么算哦)。

library(reportROC)

data(aSAH)

reportROC(gold=aSAH$outcome,predictor=aSAH$s100b)

参考文献  

Ling CX. AUC: a Better Measure than Accuracy in Comparing Learning Algorithms. http://site.uottawa.ca/~stan/csi7162/presentations/William-presentation.pdf