Bootstrap

数字信号处理（Digital Signal Procession）总结

0、导入库

import numpy as np
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import pyplot as plt
from scipy.signal import find_peaks

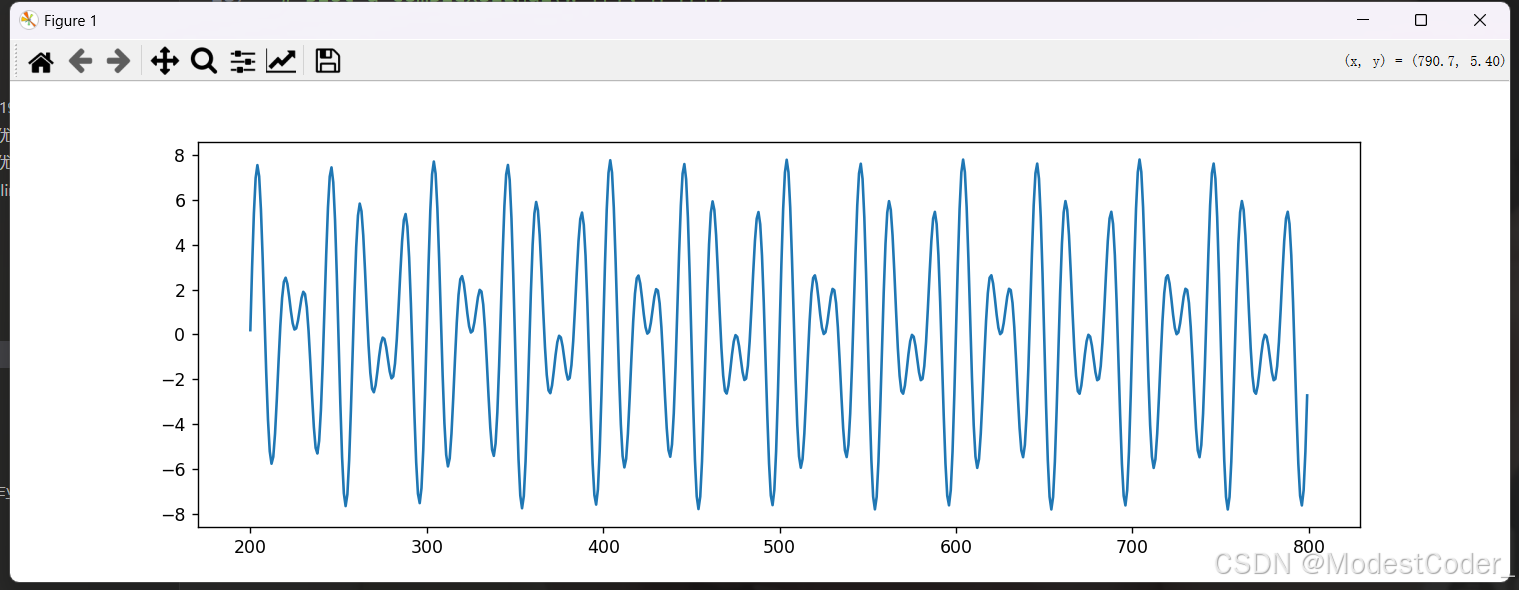
1、创建时域信号

创建时间序列
T = 0.01 # 采样间隔
fs = 100 # 采样频率
L = 1000 # 采样点数
tl = 0 # 起始时间
tr = tl + (L - 1) * T # 终止时间
t = np.linspace(tl, tr, L)
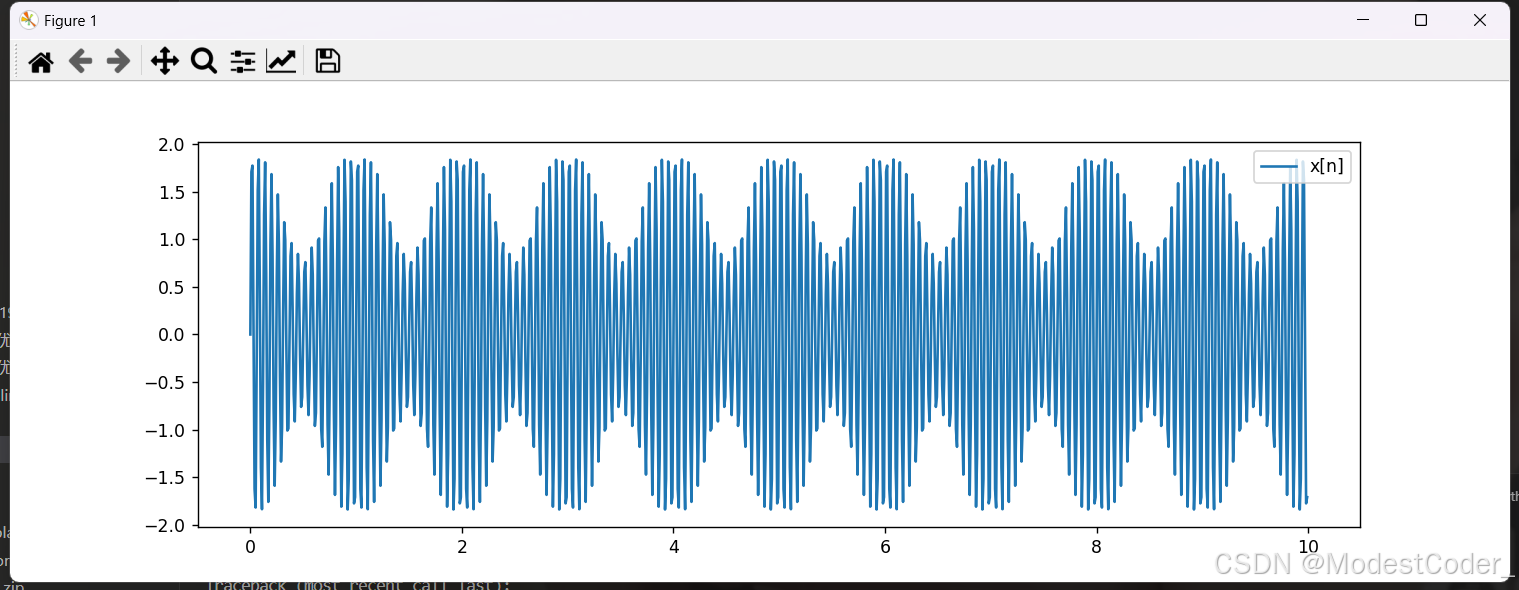
创建时域信号

以正弦信号为例

def generate_time_domain_sin_signal(t, A, f):
    pi = np.pi
    x = A * np.sin(2 * pi * f * t)
    return x

A1 = 1.4
A2 = 0.6
f1 = 16
f2 = 17
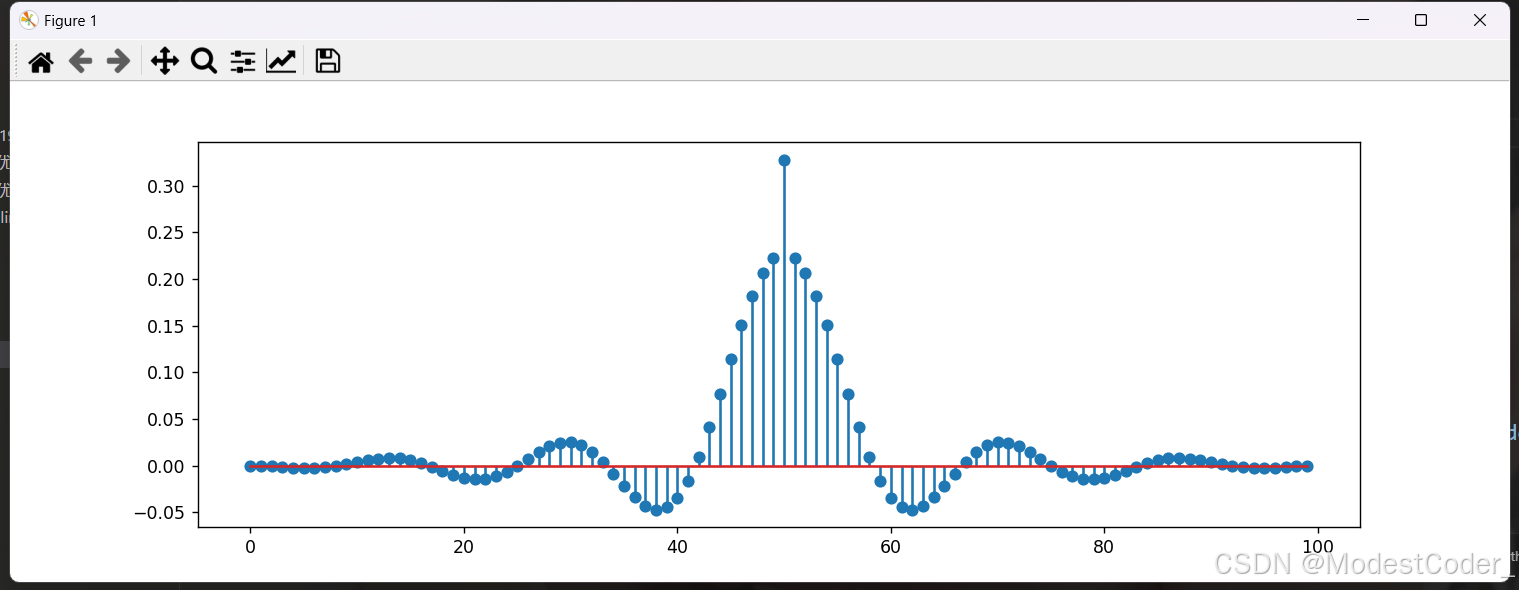
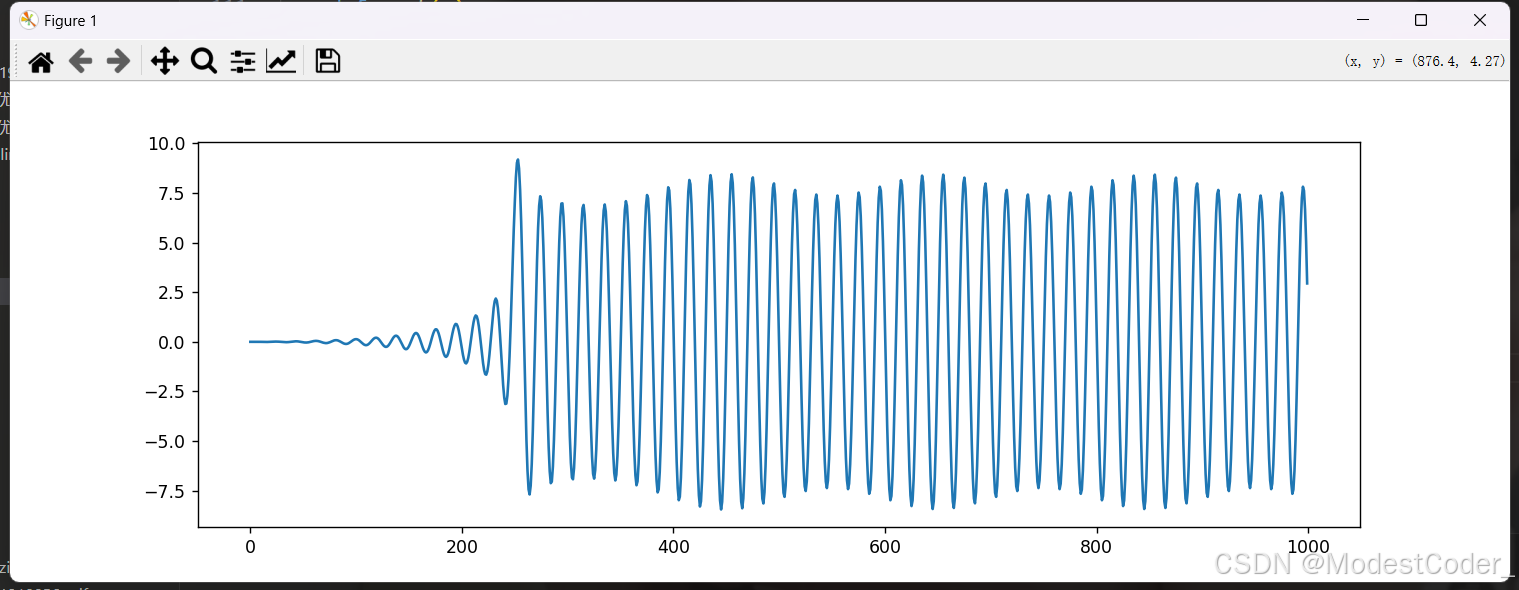
x = generate_time_domain_sin_signal(t, A1, f1) + generate_time_domain_sin_signal(t, A2, f2)

画一下，看看效果
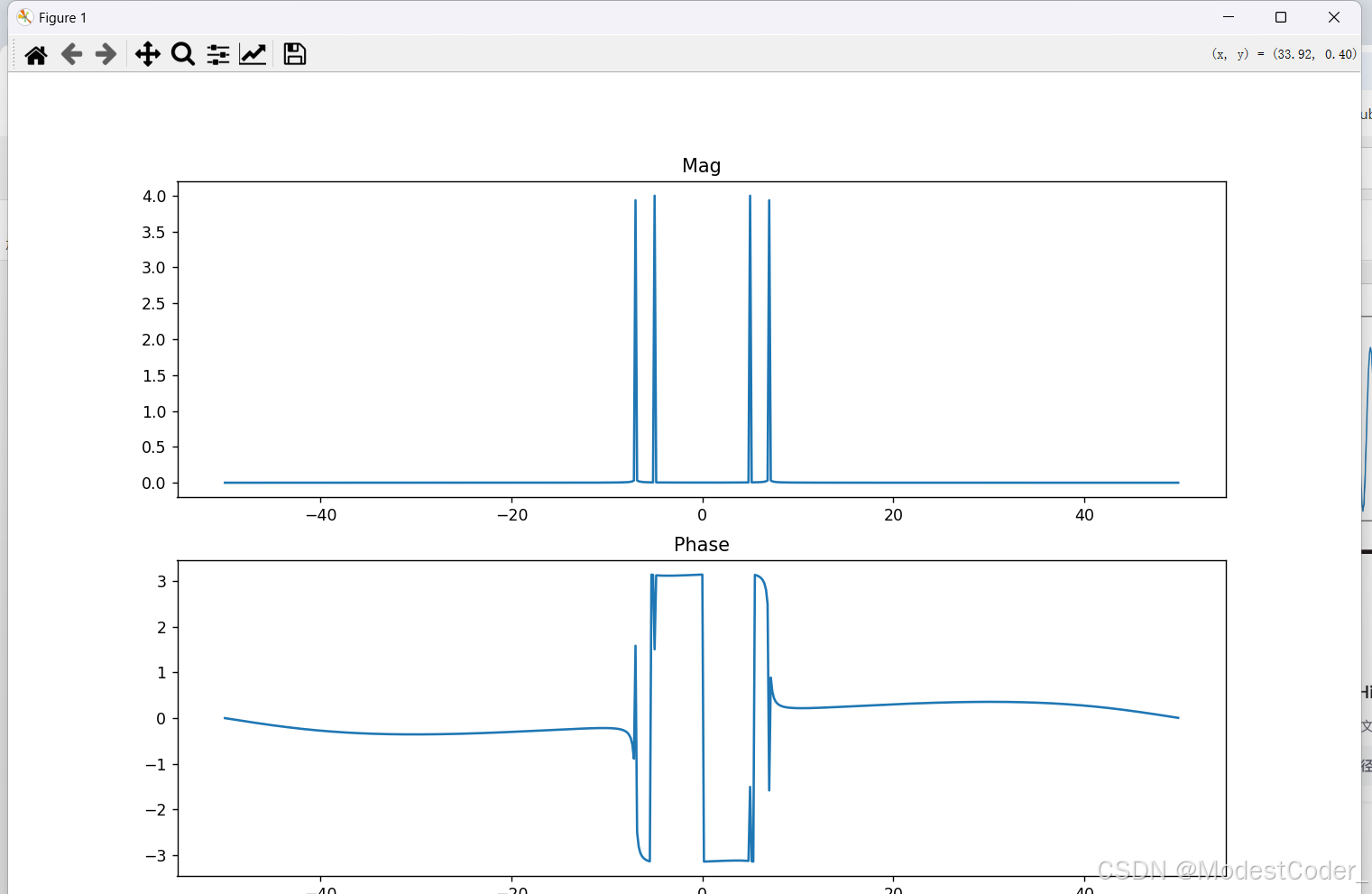
在这里插入图片描述

2、傅里叶变换

理论分析
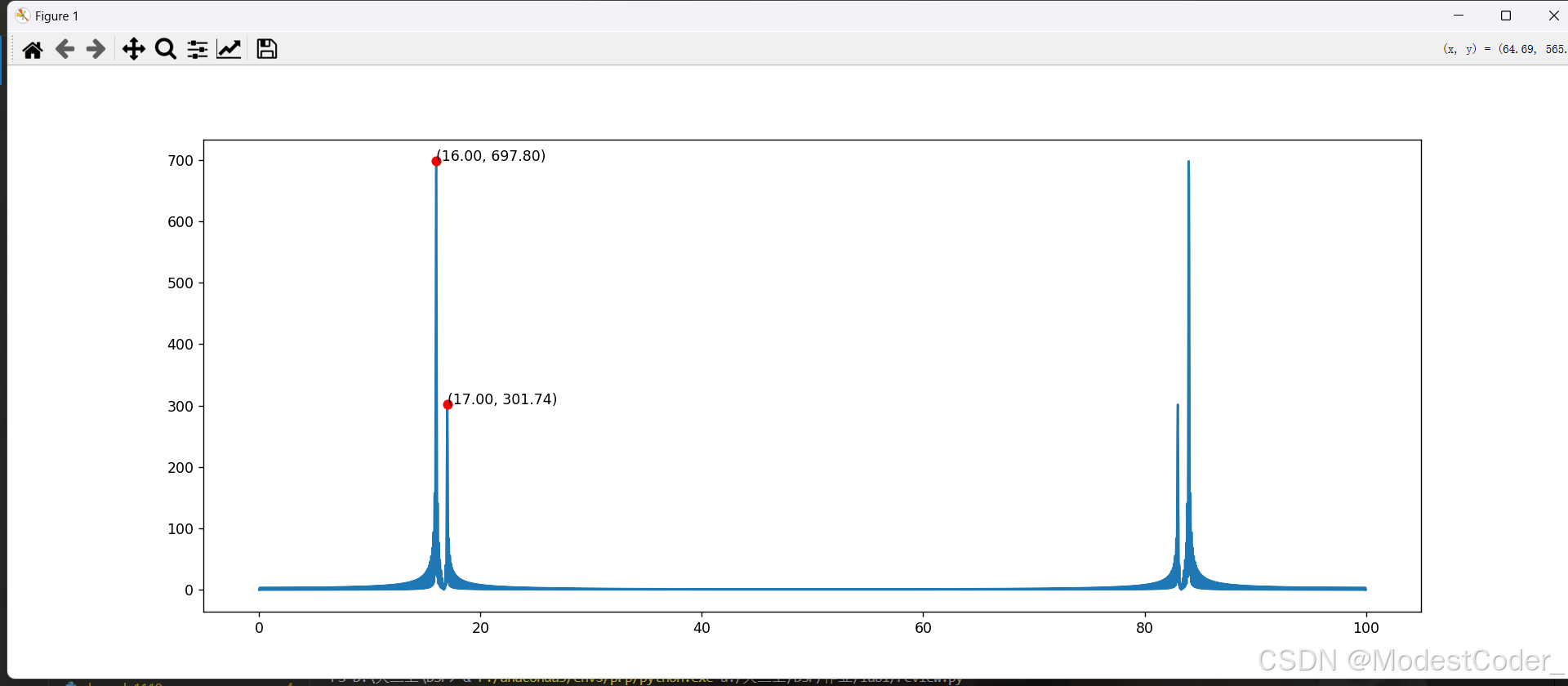
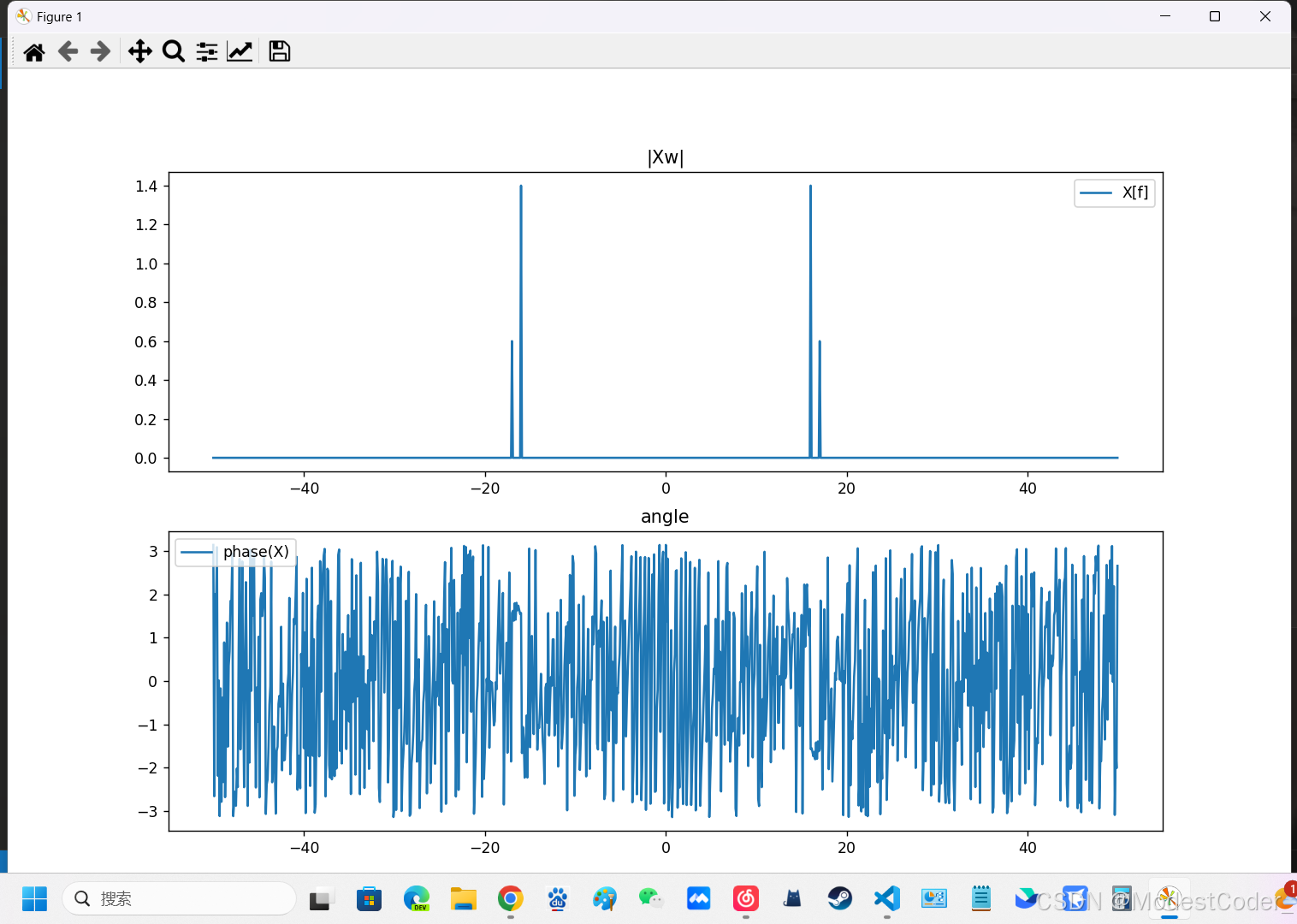
  • 原信号为正弦信号，假设频率为 f 0 f_0 f0​的分量幅值为 A 0 A_0 A0​，则傅里叶变换后，在f域中，在 f = ± f 0 f=±f_0 f=±f0​处的幅值应为 A 0 2 \frac{A_0}{2} 2A0​​;相角在 f 0 f_0 f0​处为 − 90 ° -90° −90°，在 − f 0 -f_0 −f0​处为 + 90 ° +90° +90°
  • 采样频率为 f s = 100 H z fs=100Hz fs=100Hz，相当于频域卷积梳状函数 f s δ f s ( f ) fs \delta_{fs}(f) fsδfs​(f)，体现在幅值上，应乘 f s f_s fs​
  • 原信号其实是无限信号，但是只采样了 L L L个点，相当于在 t = L ∗ T = 10 s t=L *T=10s t=L∗T=10s处截断了，相当于乘上了一个 门宽为10，门高为1的矩形窗，相当于频域卷积了一个峰值为10的sinc函数，幅值应乘 L ∗ T L * T L∗T
  • 综合以上，幅值应乘 L 2 \frac{L}{2} 2L​
  • 假如再在原信号的基础上加个别的窗，以hamming窗为例，幅值应乘hamming窗的积分，设积分为 I = ∑ h a m m i n g [ t ] d t I=\sum {hamming[t]dt} I=∑hamming[t]dt，总幅值的变化倍数为 f s 2 ∗ I = ∑ w i n d o w F u n c t i o n [ i ] 2 \frac{fs}{2}*I=\frac{\sum windowFunction[i]}{2} 2fs​∗I=2∑windowFunction[i]​
创建频率序列

在数字信号处理当中，任何信号的傅里叶变换都以奈奎斯特区间为周期，奈奎斯特区间为 [ 0 , f s ] [0, f_s] [0,fs​]，对应角频率为 w = [ 0 , 2 p i ] ∗ f s w=[0, 2pi] * fs w=[0,2pi]∗fs

批注：

奈奎斯特区间对应关系：

  • [ 0 , 1 ] [0,1] [0,1]
  • [ − 0.5 , 0.5 ] [-0.5,0.5] [−0.5,0.5]
  • [ 0 , 2 π ] [0,2 \pi] [0,2π]
  • [ − π , π ] [-\pi, \pi] [−π,π]
  • [ 0 , f s ] [0, fs] [0,fs]
  • [ − f s 2 , f s 2 ] [-\frac{fs}{2}, \frac{fs}{2}] [−2fs​,2fs​]
  • [ 0 , 2 π f s ] [0, 2 \pi fs] [0,2πfs]
  • [ − π f s , π f s ] [-\pi fs, \pi fs] [−πfs,πfs]
w = np.linspace(0, 2 * pi, SAMPLE_N) * fs
f = w / 2 / pi
做DTFT
def DTFT(nT, xn, w):
    Xw = np.zeros(len(w), dtype=complex)
    for i, wi in enumerate(w):
        Xw[i] = np.sum(xn * np.exp(-1j * wi * nT))
  #  Xw = np.fft.fft(xn)
    return Xw
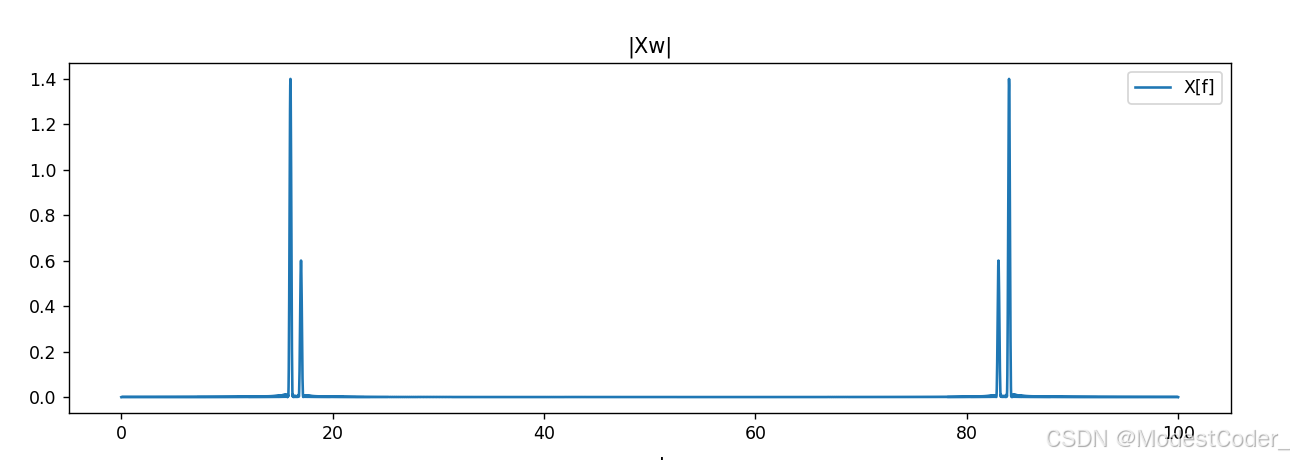
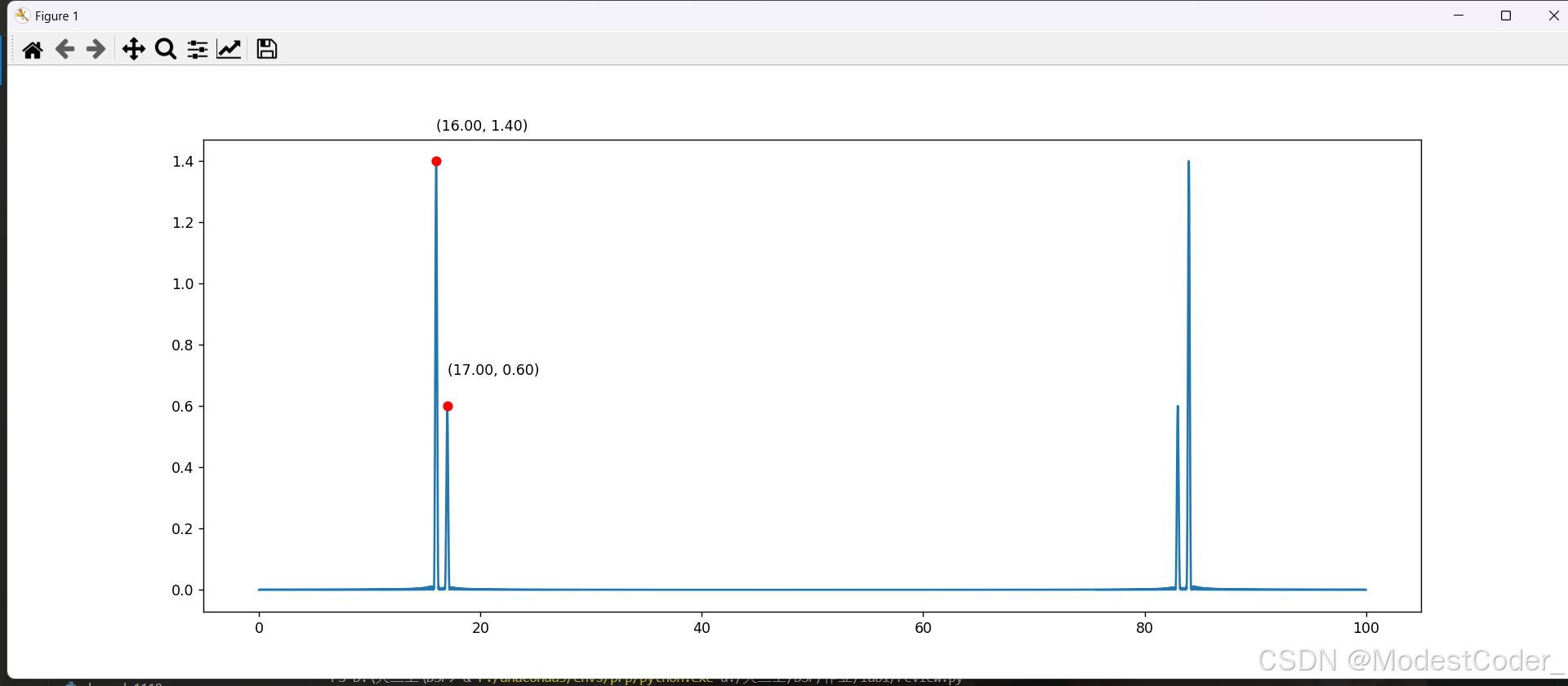
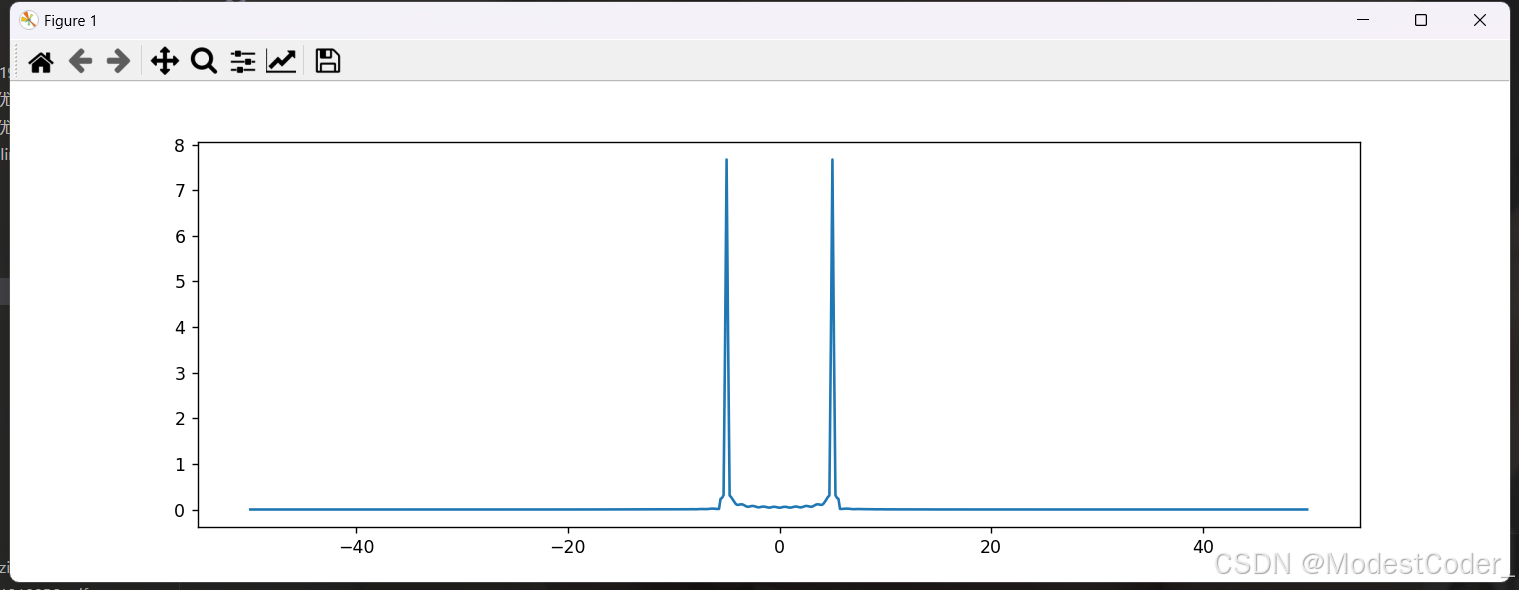
Xw = DTFT(t, x, w)

画一下，看看效果

在这里插入图片描述
幅值也满足我们的推导。

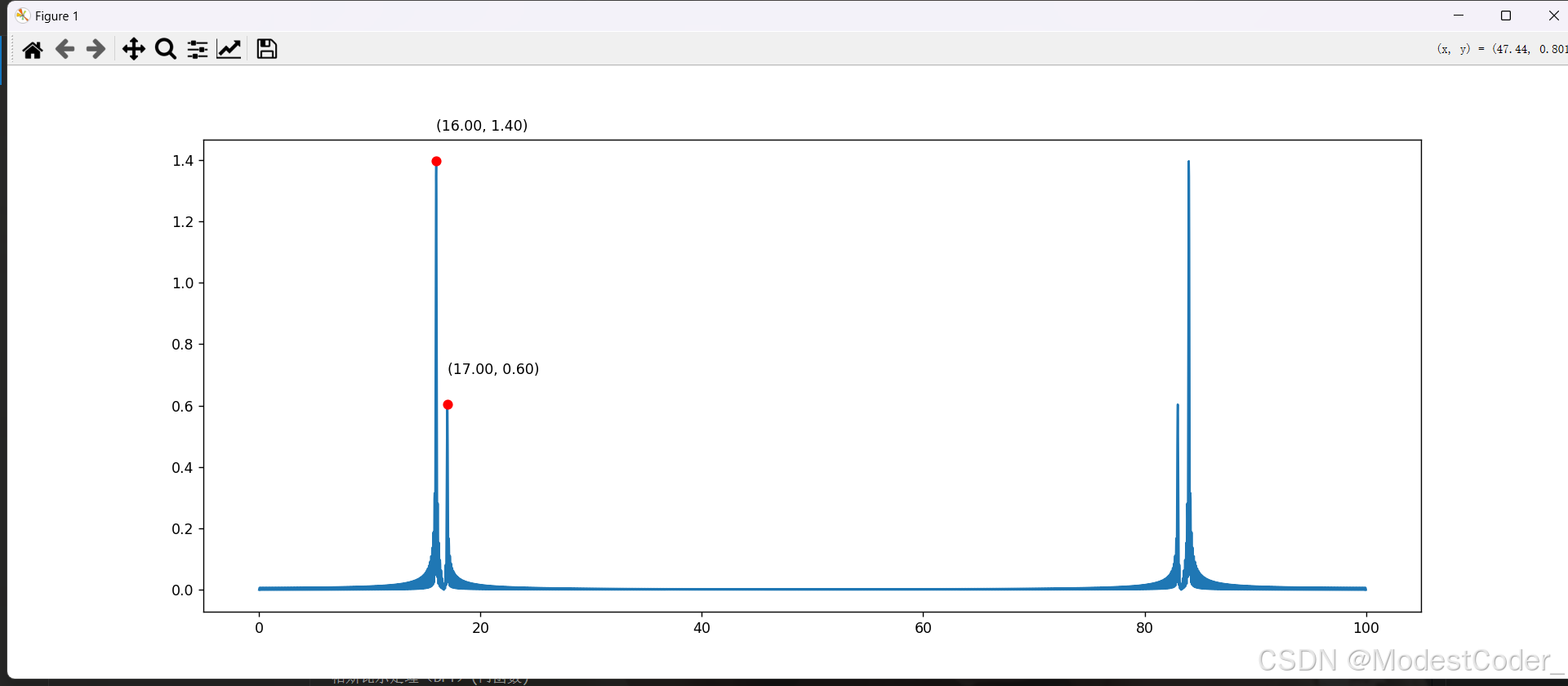
归一化

对结果乘 2 L \frac{2}{L} L2​进行归一化
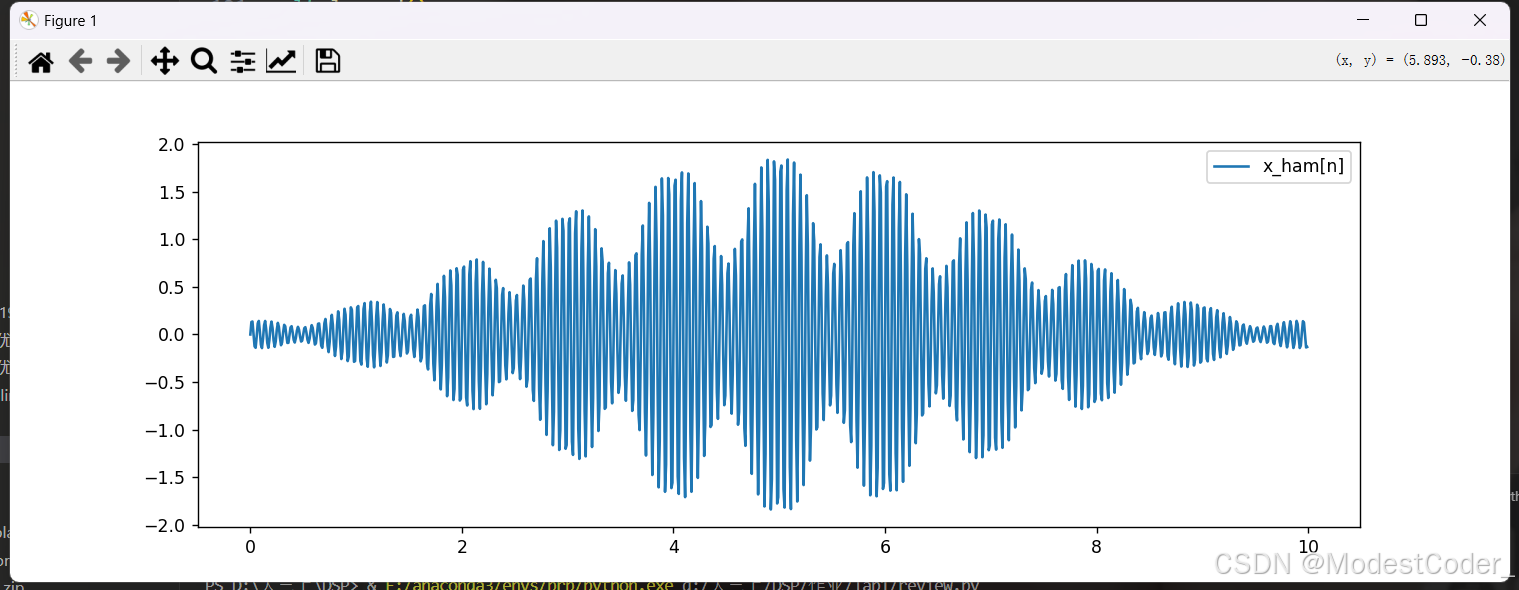
在这里插入图片描述

加窗

加个长度为 L L L和hamming窗

def hamming_window(L):
    a0 = 0.53836
    return a0 - (1 - a0) * np.cos(2 * np.pi * np.arange(L) / (L - 1))

同时要准备好hanmming窗函数的积分，用于观察幅值变换

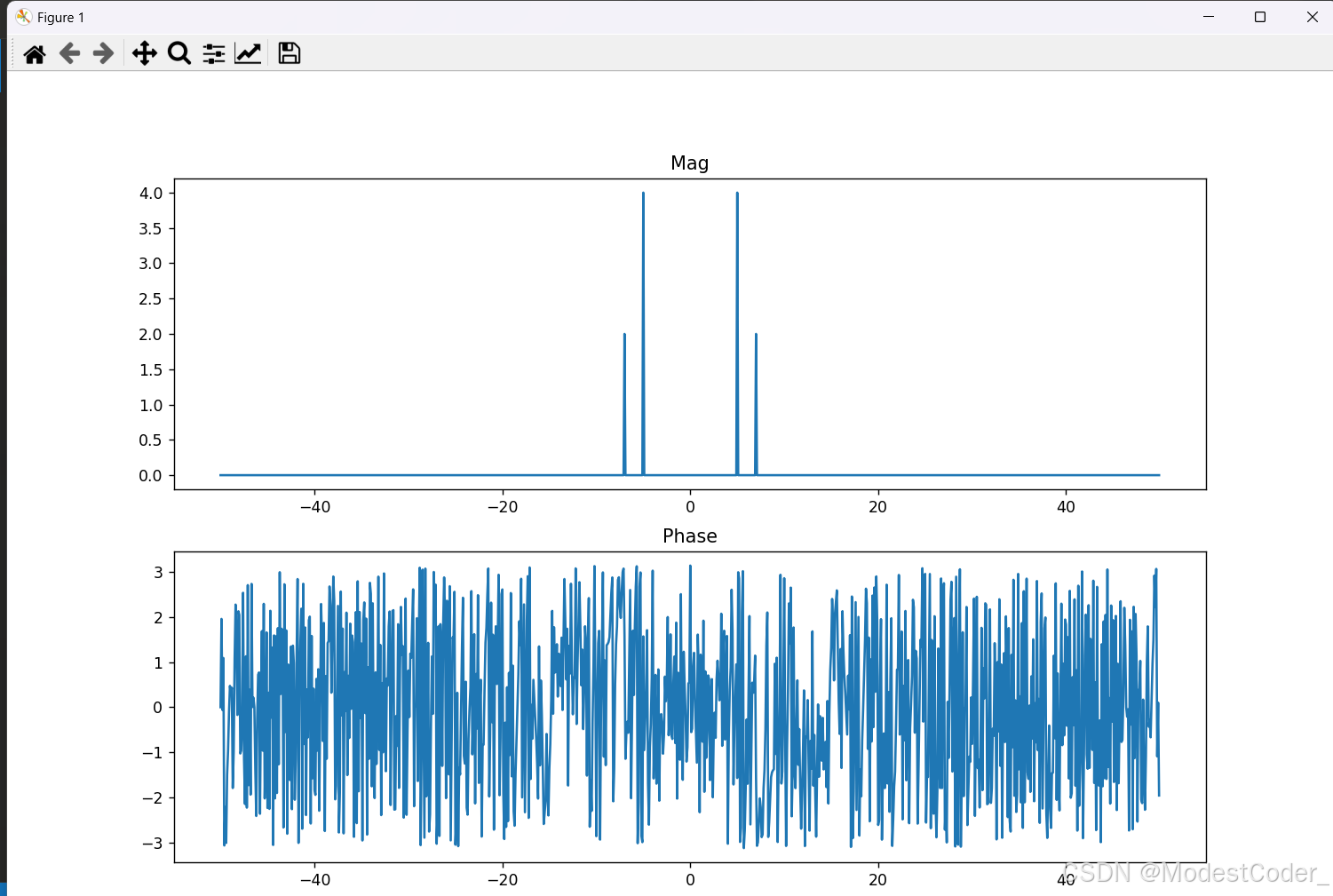
画个图，看看效果

时域
在这里插入图片描述
频域
在这里插入图片描述
在这里插入图片描述
非常nice

3、不同傅里叶变换的比较

1）CTFT
def CTFT(x, t, w):
    """
    x[i] and t[i] is the i-th sample of the signal and time,
    for each w[i], this function will calculate the CTFT of x(t) at w[i].

    ## Examples

    ```py
    def g(t):
        return np.where((t >= -4) & (t <= 4), 2, 0)

    t_values = np.linspace(-5, 9, SAMPLE_N)
    g_values = g(t_values)

    maxw = 10 * np.pi
    w_values = np.linspace(-maxw, maxw, SAMPLE_N)
    Gw = CTFT(g_values, t_values, w_values)
    ```
    """
    Xw = np.zeros_like(w, dtype=complex)
    dt = t[1] - t[0]
    for i, wi in enumerate(w):
        # Two iterators here, x and t
        Xw[i] = np.sum(x * np.exp(-1j * wi * t) * dt)
    return Xw

正弦谐波做完CTFT的结果：

在这里插入图片描述

相比于DTFT，CTFT在计算机当中的做法就是用DTFT实现CTFT的效果，但是多乘了个 d t dt dt

2）DTFT

已做过

3）DFT
def DFT(ys):
    """
    Calculate the Discrete Fourier Transform of the signal `ys`,
    which is an N-point sampling of the DTFT of the signal. 

    ## Examples

    ```py
    y = np.array([-1, 2, 3, 0, -2, 1, 4, -3, 0, -2])
    dft_w_vec, dft_vec = DFT(y)
    debug_draw(dft_w_vec, np.abs(dft_vec))
    ```
    """
    n = len(ys)
    ns = np.arange(n)

    def omega_k(k):
        return 2 * np.pi * k / n
    w_vec = np.array([omega_k(k) for k in range(n)])
    dft_vec = np.array([sum(ys * np.exp(-1j * w * ns)) for w in w_vec])
    return w_vec, dft_vec

其中w_vec为数字角频率，范围为 [ 0 , 2 p i ] [0,2pi] [0,2pi]，若要映射到范围 [ 0 , f s ] [0,fs] [0,fs],则需变换一下

w_dft, Xw_dft = DFT(x)
f_dft = w_dft / 2 / pi * fs

画一下，看看效果
在这里插入图片描述

同时我们还可以使用FFT实现

n_dft = len(x)
Xw_dft = np.fft.fft(x)
Xw_dft = np.fft.fftshift(Xw_dft)
f_dft = np.fft.fftfreq(n_dft, T)
f_dft = np.fft.fftshift(f_dft)

画一下，看看效果

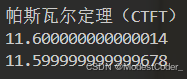
在这里插入图片描述

4、帕斯瓦尔定理的验证

CTFT
print("帕斯瓦尔定理（CTFT）")
energy_time_domain = np.sum(np.abs(x) ** 2) * (t[1] - t[0])
energy_freq_domain = np.sum(np.abs(Xw) ** 2) * (f[1] - f[0])
print(energy_time_domain)
print(energy_freq_domain)
print("-------------")

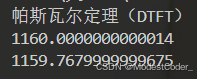
在这里插入图片描述

DTFT
print("帕斯瓦尔定理（DTFT）")
energy_time_domain = np.sum(np.abs(x) ** 2)
energy_freq_domain = np.sum(np.abs(Xw) ** 2) / len(Xw)
print(energy_time_domain)
print(energy_freq_domain)
print("-------------")

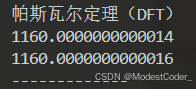
在这里插入图片描述

DFT
print("帕斯瓦尔定理（DFT）")
energy_time_domain = np.sum(np.abs(x) ** 2)
energy_freq_domain = np.sum(np.abs(Xw_dft) ** 2) / n_dft
print(energy_time_domain)
print(energy_freq_domain)
print("-------------")

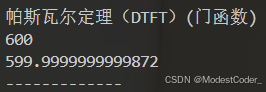
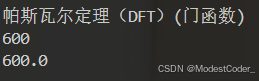
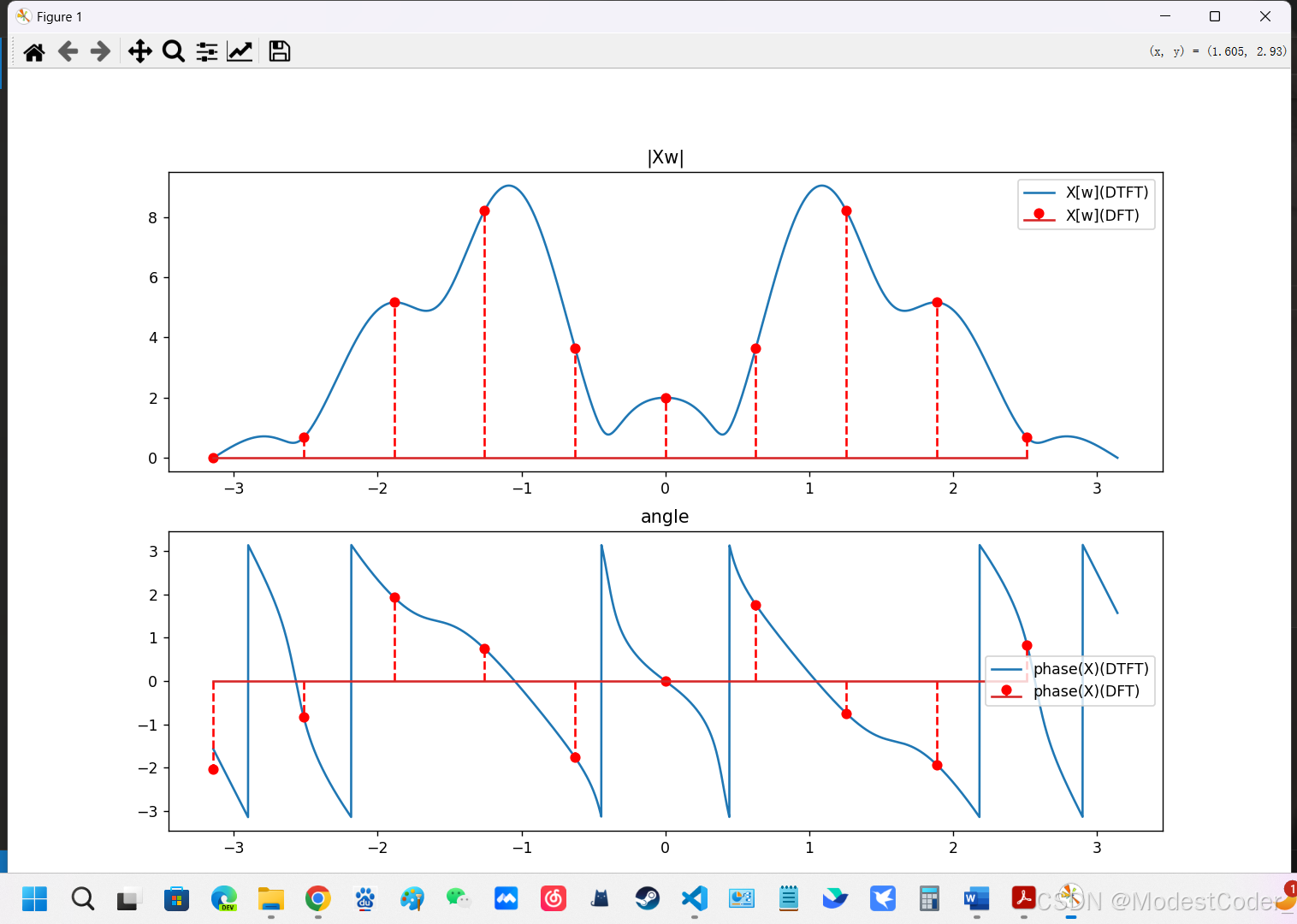
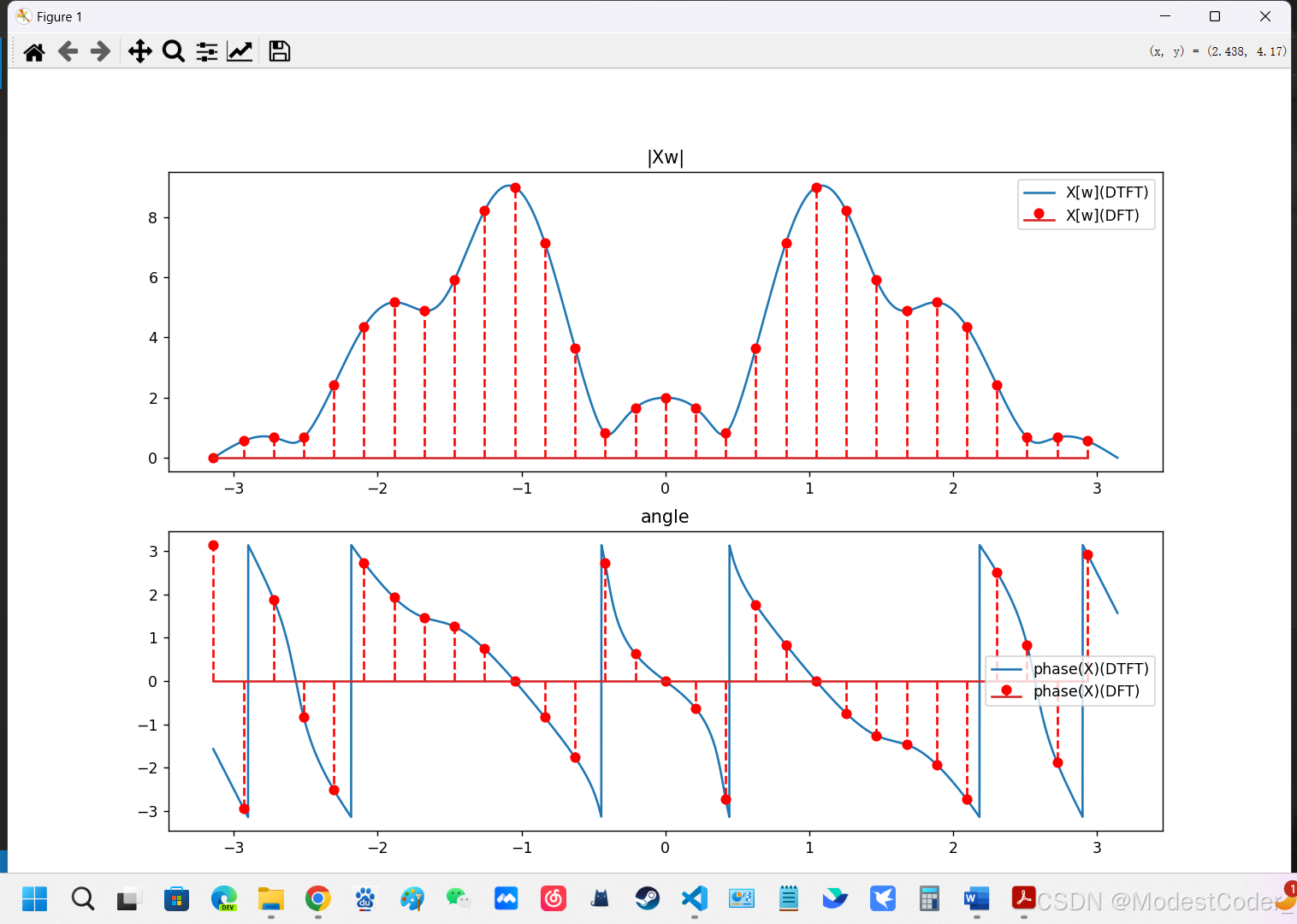
在这里插入图片描述

门函数的帕斯瓦尔定理

换一个信号，这次选择门函数，验证帕斯瓦尔定理是否正确

tl1 = 0
tr1 = 10
T = 0.01
fs = 100
L = 1000
t1 = np.linspace(tl1, tr1, L)
t1 = np.around(t1, 2)
x1 = np.where((t1 >= 2) & (t1 <= 8), 1, 0)

w = np.linspace(0, 2 * pi, SAMPLE_N, endpoint=False) * fs
DTFT
Xw1 = DTFT(t1, x1, w)
print("帕斯瓦尔定理（DTFT）(门函数)")
energy_time_domain = np.sum(np.abs(x1) ** 2)
energy_freq_domain = np.sum(np.abs(Xw1) ** 2) / len(Xw1)
print(energy_time_domain)
print(energy_freq_domain)
print("-------------")

在这里插入图片描述

CTFT
Xw1 = CTFT(x1, t1, w)
print("帕斯瓦尔定理（CTFT）(门函数)")
energy_time_domain = np.sum(np.abs(x1) ** 2) * (t[1] - t[0])
energy_freq_domain = np.sum(np.abs(Xw1) ** 2) * (f[1] - f[0])
print(energy_time_domain)
print(energy_freq_domain)
print("-------------")

在这里插入图片描述

DFT
n1_dft = len(x1)
Xw1_dft = np.fft.fft(x1)
Xw1_dft = np.fft.fftshift(Xw1_dft)
f1_dft = np.fft.fftfreq(n1_dft, T)
f1_dft = np.fft.fftshift(f1_dft)
print("帕斯瓦尔定理（DFT）(门函数)")
energy_time_domain = np.sum(np.abs(x1) ** 2)
energy_freq_domain = np.sum(np.abs(Xw1_dft) ** 2) / n_dft
print(energy_time_domain)
print(energy_freq_domain)
print("-------------")

在这里插入图片描述

5、FFT

基本操作

对一个离散时间序列 x [ n ] x[n] x[n]

SAMPLE_N = 5000
pi = np.pi

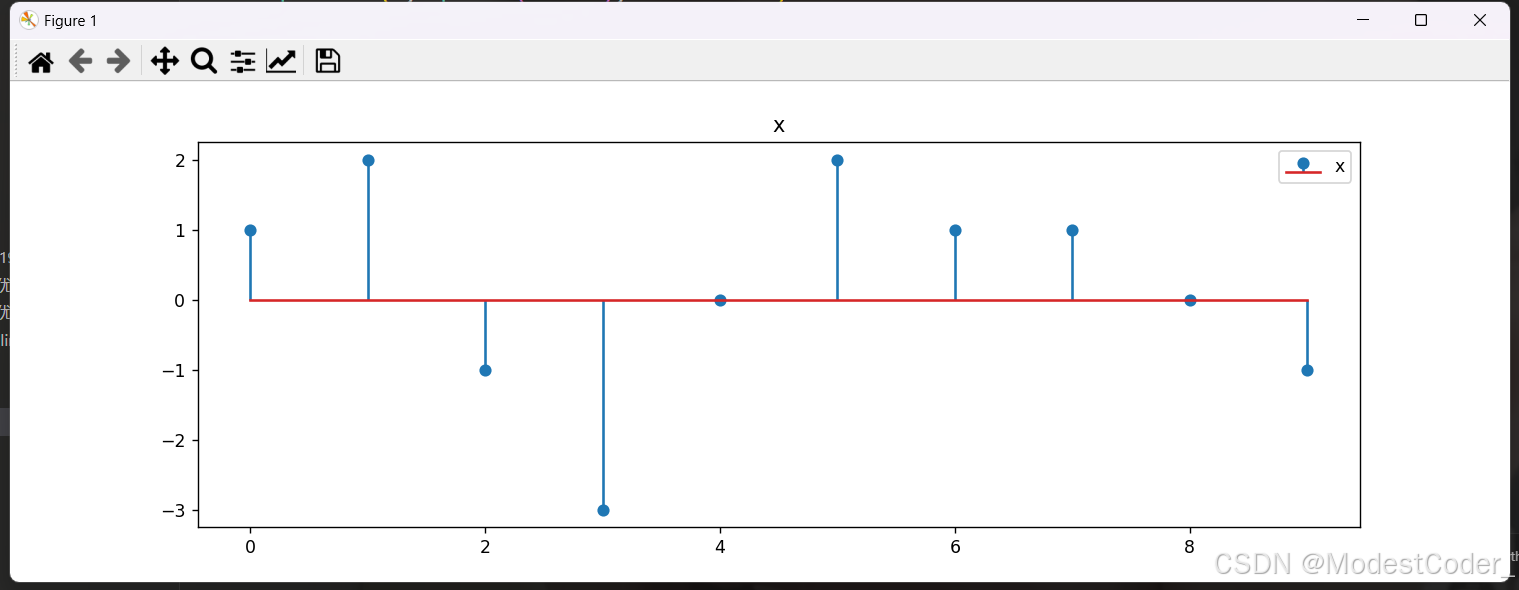
x = np.array([1, 2, -1, -3, 0, 2, 1, 1, 0, -1])
N = len(x)
n = np.arange(N)

做FFT，做完之后，通过fftshift将零频率移到数组的中间

Xw_dft = np.fft.fft(x)
Xw_dft = np.fft.fftshift(Xw_dft)
w_dft = np.fft.fftfreq(N, 1)
w_dft = np.fft.fftshift(w_dft)

比较DTFT与FFT的结果
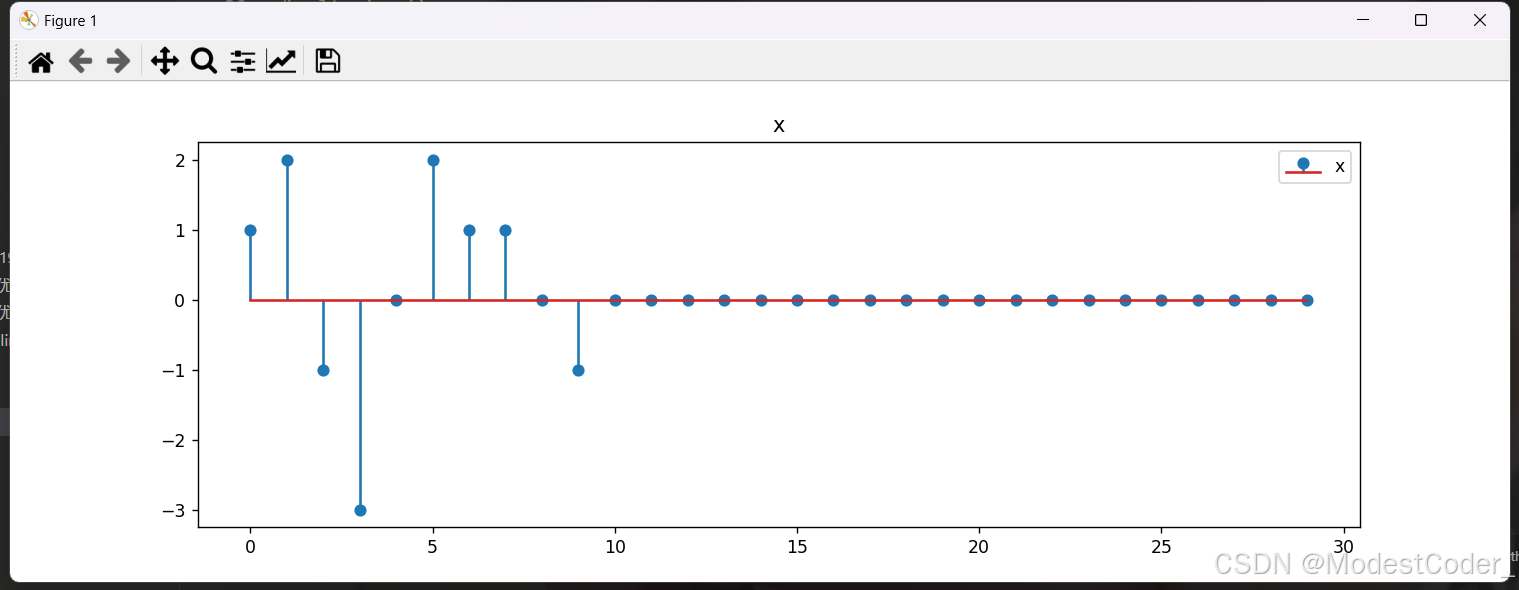
在这里插入图片描述

zero-padding

在时间序列的最后进行zero_padding，可以增加点数且不改变频率信号的形状

x = np.append(x, np.zeros(20))
N = len(x)
n = np.arange(N)

再次画图
在这里插入图片描述

ifft

n p . f f t . i f f t np.fft.ifft np.fft.ifft使用时需要注意：传进去的数组必须是[零频率项，正频率项，负频率项]
不能将fftshift过的数组传进去
画一下

在这里插入图片描述

跟原数组一样

在这里插入图片描述
zero-padding后也一样

6、FIR滤波器-频率采样法设计滤波器

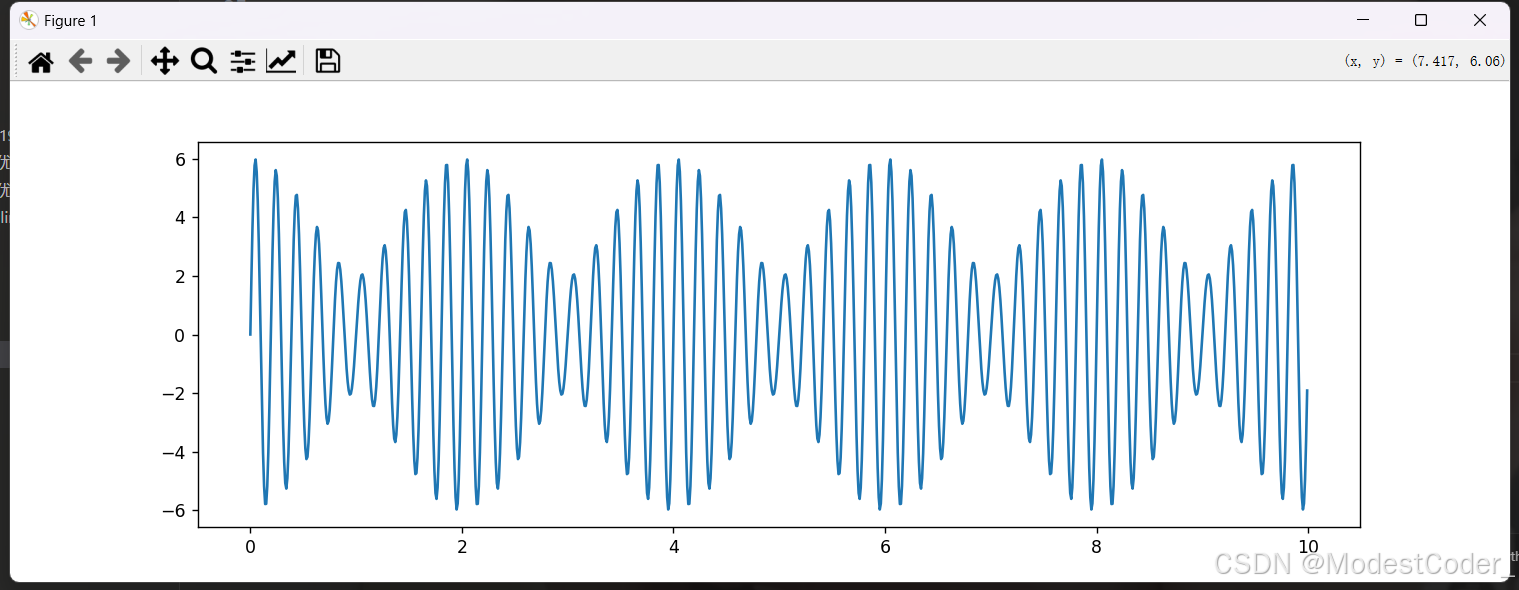
创建时域信号

先准备一个时域信号，简单包含不同幅值，频率分别为 f 1 = 5 H z , f 2 = 5.5 H z f1=5Hz,f2=5.5Hz f1=5Hz,f2=5.5Hz的两个正弦波叠加，采样频率为 f s = 100 H z fs = 100Hz fs=100Hz，采 L = 1000 L = 1000 L=1000个点

T = 0.01
fs = 100
A1 = 4
A2 = 2
f1 = 5
f2 = 5.5
L = 1000
t = np.linspace(0, (L - 1) * T, L)
t = np.around(t, 2)
x = generate_time_domain_sin_signal(t, A1, f1) + generate_time_domain_sin_signal(t, A2, f2)

画一画x[n]与X[f]

在这里插入图片描述
在这里插入图片描述

可以发现，频谱中有5Hz与5.5Hz两个分量

频域采样

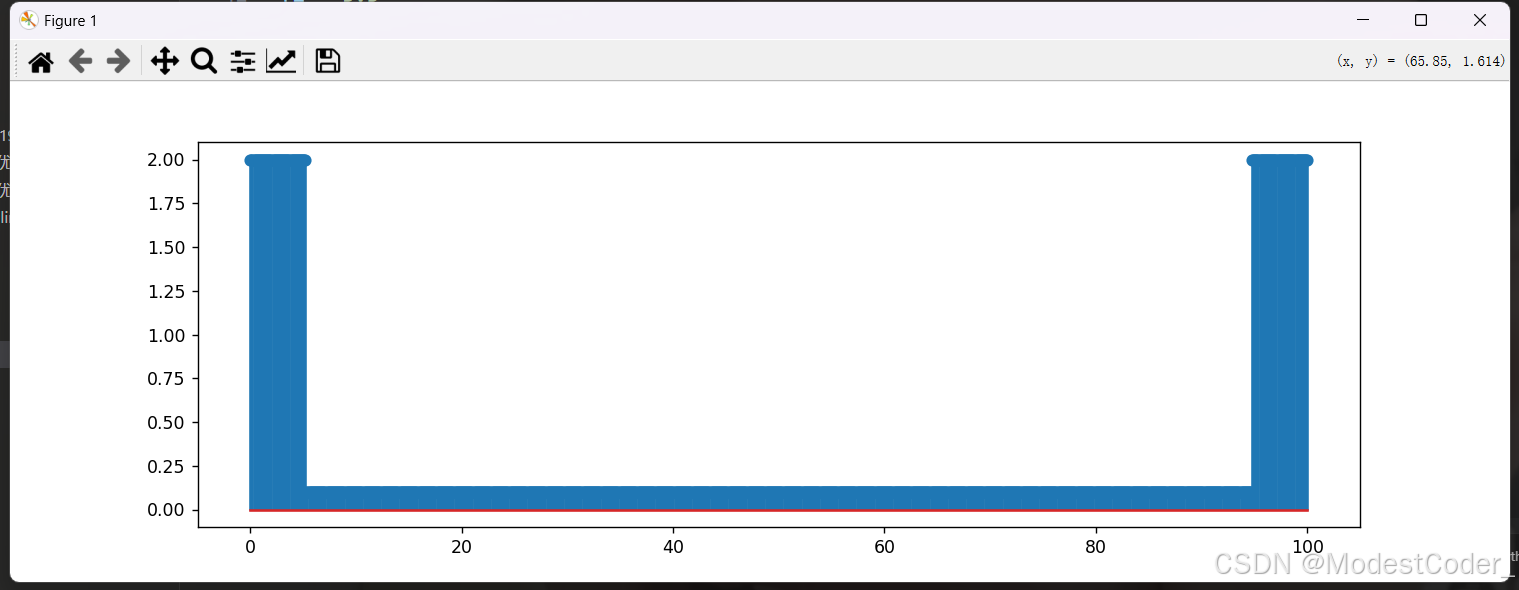
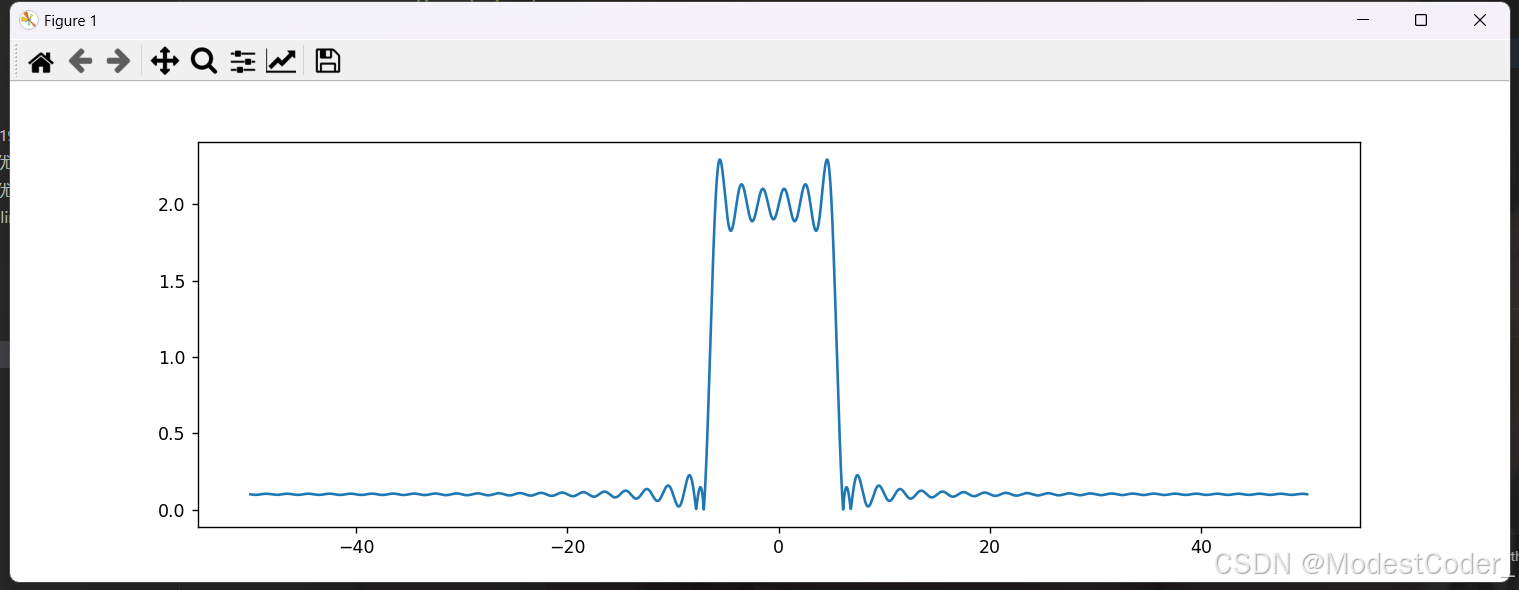
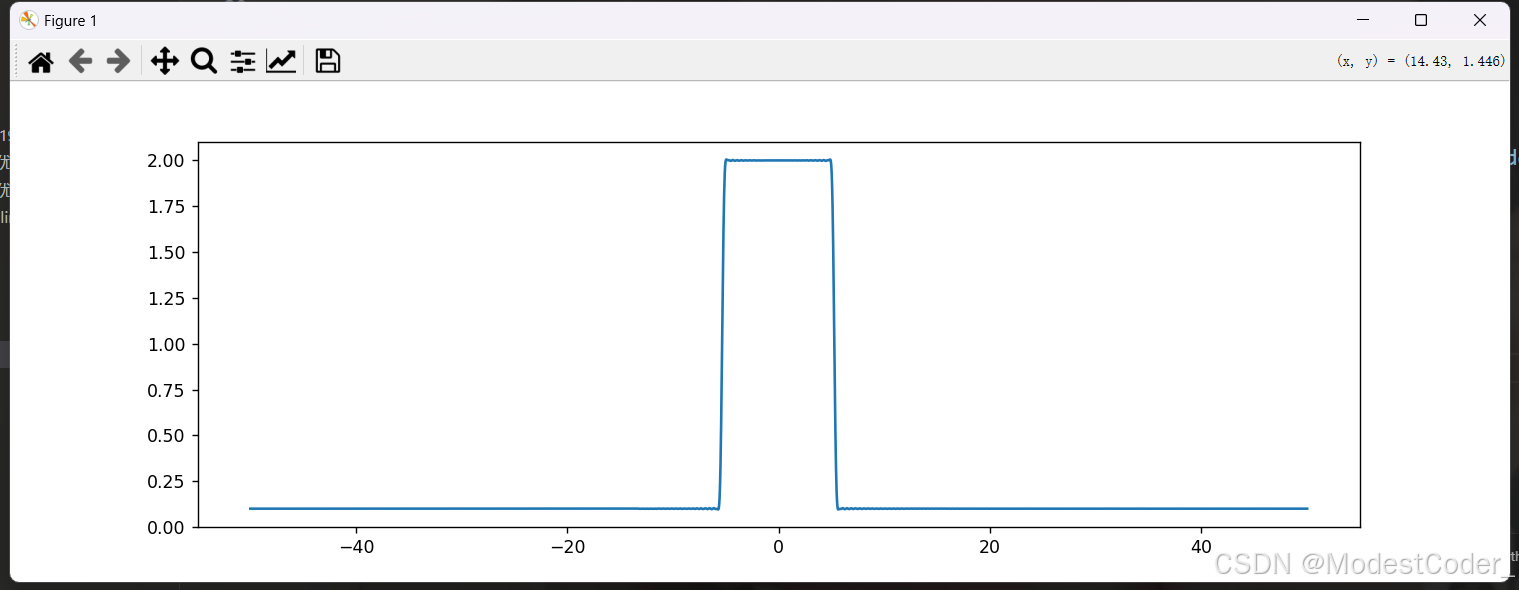
设计一个低通滤波器，把5.5Hz滤掉。
在一个ideal的低通滤波器上采样，设置截止频率为5.25Hz，通带增益为2，阻带增益为0.1

def generate_lowpass_signal(fc, n_samples, passband, stopband):
    w = np.linspace(0, 2 * pi, n_samples)
    h = np.zeros(n_samples, dtype=complex)
    for i, wi in enumerate(w):
        if (wi <= fc or wi >= 2 * pi - fc):
            h[i] = passband
        else:
            h[i] = stopband
    return h, w

orders = 1000
H, wh = generate_lowpass_signal(5.25 / (fs / 2) * pi, orders, 2, 0.1)

画一画
在这里插入图片描述
画出来也是挺ideal的！

反傅里叶变换

对采出来的滤波器数组进行 i f f t ifft ifft
要注意传进去的数组 遵循【零频率，正频率，负频率】顺序，我们是 [ 0 , 2 π ] [0,2\pi] [0,2π]，刚刚好！
做了 i f f t ifft ifft之后也要将零频率移到数组中间

h = np.fft.ifft(H)
h = np.fft.ifftshift(h)
n = np.arange(orders)

画一画，这里将阶数改为100了，因为1000太丑了
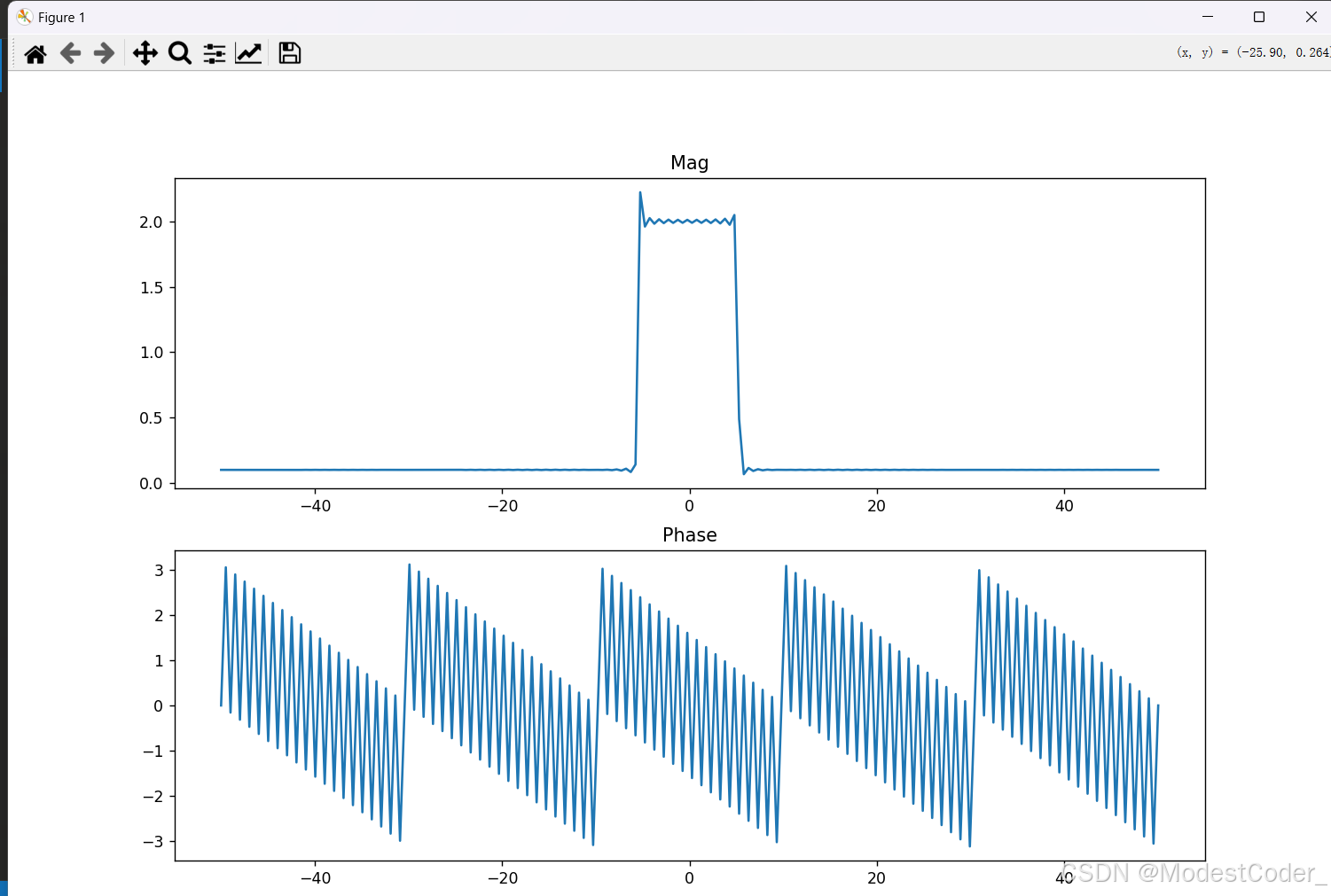
在这里插入图片描述

求滤波器的频率响应

先准备一个频率序列 w w w，在 [ − π , π ] [-\pi, \pi] [−π,π]中取几千个点

  • 对于FIR滤波器， h [ n ] = b [ n ] , a [ n ] = [ 1 , 0 , 0... ] h[n]=b[n],a[n]=[1,0,0...] h[n]=b[n],a[n]=[1,0,0...]
  • 对于IIR滤波器，也不需要用频率采样哈哈哈
def freqz(bz, az, w):
    def cap_h_value(bz, az, z: complex):
        num = sum([bz[i] * z ** (-i) for i in range(len(bz))])
        den = sum([az[i] * z ** (-i) for i in range(len(az))])
        return num / den
    cap_hs = np.array([cap_h_value(bz, az, np.exp(1j * omega)) for omega in w])
    return cap_hs  # values of H(w)


w_frf = np.linspace(-pi, pi, SAMPLE_N)
H_frf = freqz(h, [1], w_frf)

画一画

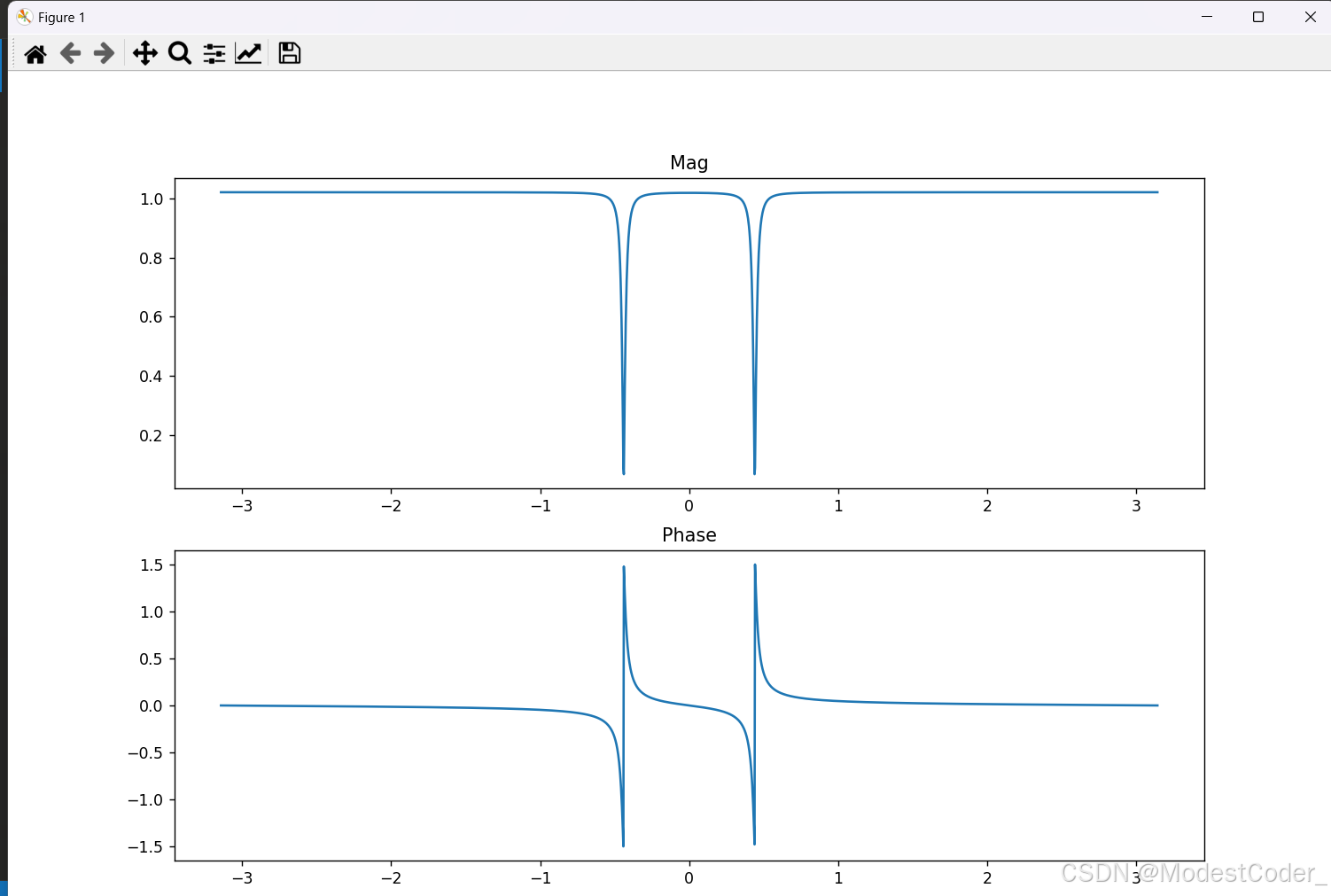
在这里插入图片描述
发现还是频谱泄露了很多

缓解频谱泄漏：加个窗

对于一个滤波器序列，序列长度为 o r d e r s orders orders，其零频率在序列中间
加个窗， 长度为 w i n d o w O r d e r windowOrder windowOrder，通常加窗还有一个功能就是减少阶数，所以 w i n d o w O r d e r < o r d e r s windowOrder<orders windowOrder<orders
巧的是，窗函数序列的零频率也在中间

所以有

def hamming_window(L):
    a0 = 0.53836
    return a0 - (1 - a0) * np.cos(2 * np.pi * np.arange(L) / (L - 1))

h = h[orders // 2 - window_order // 2 : orders // 2 + window_order // 2] * hamming_window(window_order)

这里以hamming窗为例了

加了窗之后再画一下频响，简直眉清目秀！

在这里插入图片描述
FIR滤波器的相位谱为线性相位，专门只取了200个点，看看相位：
在这里插入图片描述

滤波
def filter(bz, az, x, L):
    def expand(arr, n):
        return np.pad(arr, (0, n - len(arr)), 'constant')
    xs = expand(x, L)
    ys = np.zeros_like(xs)

    def y_at(n):
        return 0 if n < 0 else ys[n]

    def x_at(n):
        return 0 if n < 0 else xs[n]
    for n in range(L):
        ys[n] = sum([bz[i] * x_at(n - i) for i in range(len(bz))]) - \
            sum([az[i] * y_at(n - i) for i in range(1, len(az))])
    return xs, ys

x, y = filter(h, [1], x, L)

这里的阶数设置为500
滤波结果存在y里面

滤波结果分析

滤完之后，首先y的结果，需要把暂态的部分去掉，只看稳态部分
在这里插入图片描述
发现大概300~1000为稳态
把这一部分取出，再加窗缓解频谱泄漏

y = y[300 : 1000] * hamming_window(700)

画一画y的频谱

Yw = np.fft.fft(y)
Yw = np.fft.fftshift(Yw)
w = np.fft.fftfreq(700, T)
w = np.fft.fftshift(w)

plot_a_signal(w, np.abs(Yw) * 2 / hamming_intergal(700))

在这里插入图片描述

发现5.5Hz的成分已经被消灭了，且幅值满足增益为2的设定。

7、零极点设计滤波器

1）陷状滤波器

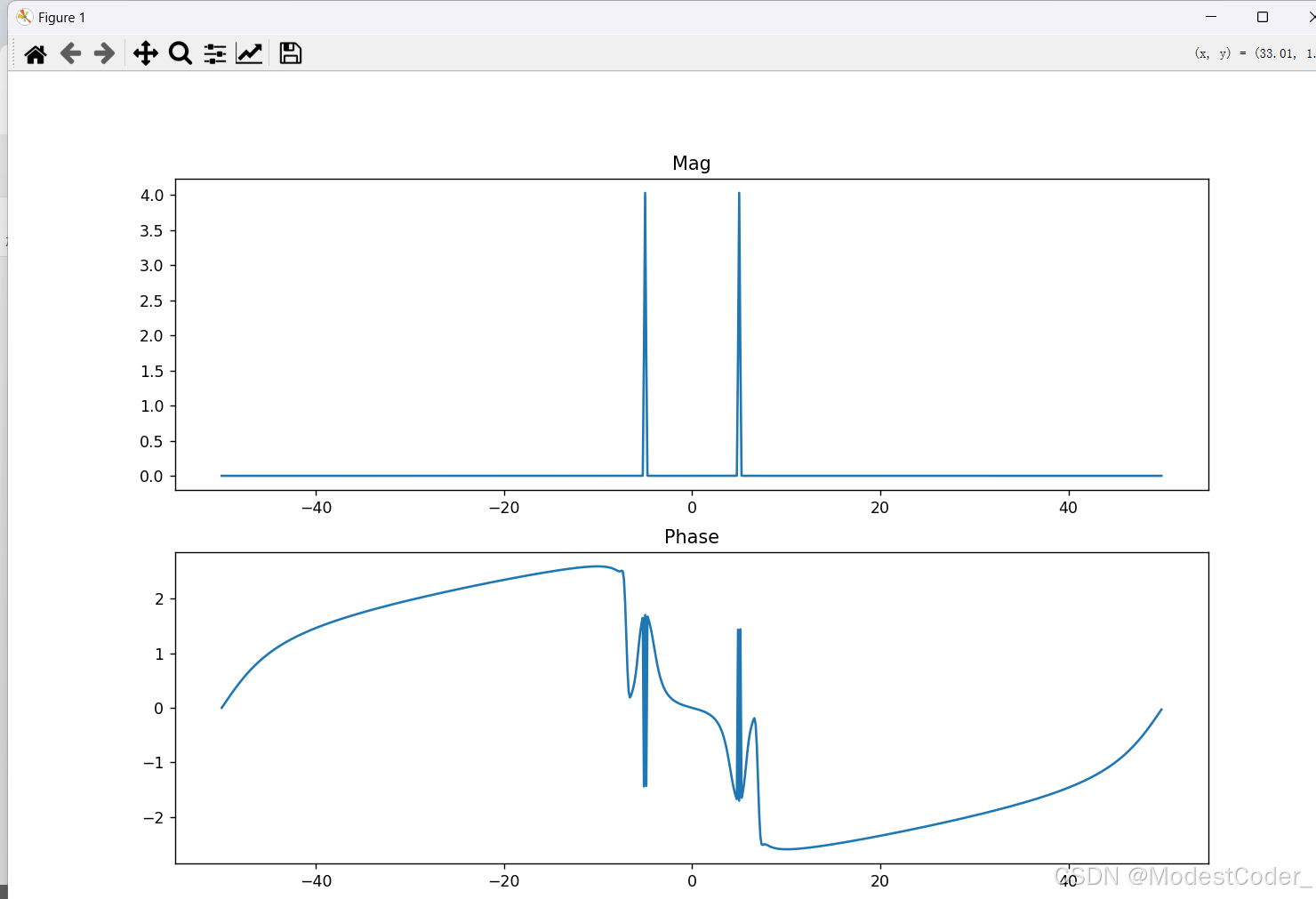
假如说一个 f s = 100 H z fs=100Hz fs=100Hz,包含两个频率分量 f 1 = 5 H z , f 2 = 5.5 H z f1=5Hz,f2=5.5Hz f1=5Hz,f2=5.5Hz的正弦叠加信号，要设计一个陷状滤波器把5.5Hz分量滤掉

分析

被滤掉的频率为 f 0 , 对应角度为 ω 0 = f 0 f s 2 π 被滤掉的频率为f0,对应角度为\omega _0 = \frac{f0}{\frac{fs}{2}}\pi 被滤掉的频率为f0,对应角度为ω0​=2fs​f0​π
H ( z ) = ( z − z 1 ) ( z − z 2 ) ( z − p 1 ) ( z − p 2 ) = 1 − ( z 1 + z 2 ) z − 1 + z 1 z 2 z − 2 1 − ( p 1 + p 2 ) z − 1 + p 1 p 1 z − 2 = b 0 z 0 + b 1 z − 1 + b 2 z − 2 a 0 z 0 + a 1 z − 1 + a 2 z − 2 H(z)=\frac{(z-z1)(z-z2)}{(z-p1)(z-p2)}=\frac{1-(z1+z2)z^{-1}+z1z2z^{-2}}{1-(p1+p2)z^{-1}+p1p1z^{-2}}=\frac{b0z^0+b1z^{-1}+b2z^{-2}}{a0z^0+a1z^{-1}+a2z^{-2}} H(z)=(z−p1)(z−p2)(z−z1)(z−z2)​=1−(p1+p2)z−1+p1p1z−21−(z1+z2)z−1+z1z2z−2​=a0z0+a1z−1+a2z−2b0z0+b1z−1+b2z−2​
其中 z 1 = e j ω 0 , z 2 = e − j ω 0 , p 1 = Q z 1 , p 2 = Q z 2 ( 0 < Q < 1 ) 其中z1=e^{j\omega _0}, z2 = e^{-j \omega _0},p1 = Qz1, p2 = Qz2(0<Q<1) 其中z1=ejω0​,z2=e−jω0​,p1=Qz1,p2=Qz2(0<Q<1)
b 0 = 1 , b 1 = − 2 c o s ω 0 , b 2 = 1 , a 0 = 1 , a 1 = − 2 Q c o s ω 0 , a 2 = Q 2 b0=1,b1=-2cos \omega _0, b2 = 1, a0 = 1, a1 = -2Qcos \omega _0, a2 = Q^2 b0=1,b1=−2cosω0​,b2=1,a0=1,a1=−2Qcosω0​,a2=Q2

创建时域信号

先创建一个时域信号

T = 0.01
fs = 100
A1 = 4
A2 = 2
f1 = 5
f2 = 7
f0 = 7
L = 1000

t = np.linspace(0, T * L, L, endpoint=False)
t = np.around(t, 2)
x = generate_time_domain_sin_signal(t, A1, f1) + generate_time_domain_sin_signal(t, A2, f2)

画一画
在这里插入图片描述

频域分析

分析原始信号的频域

Xw = np.fft.fft(x)
Xw = np.fft.fftshift(Xw)
w = np.fft.fftfreq(L, T)
w = np.fft.fftshift(w)

在这里插入图片描述

跟想的一样

构造滤波器
a = [1]
b = [1]
w0 = f0 / (fs / 2) * pi
Q = 0.98

a = np.array([1, -2 * Q * np.cos(w0), Q ** 2])
b = np.array([1, -2 * np.cos(w0), 1])

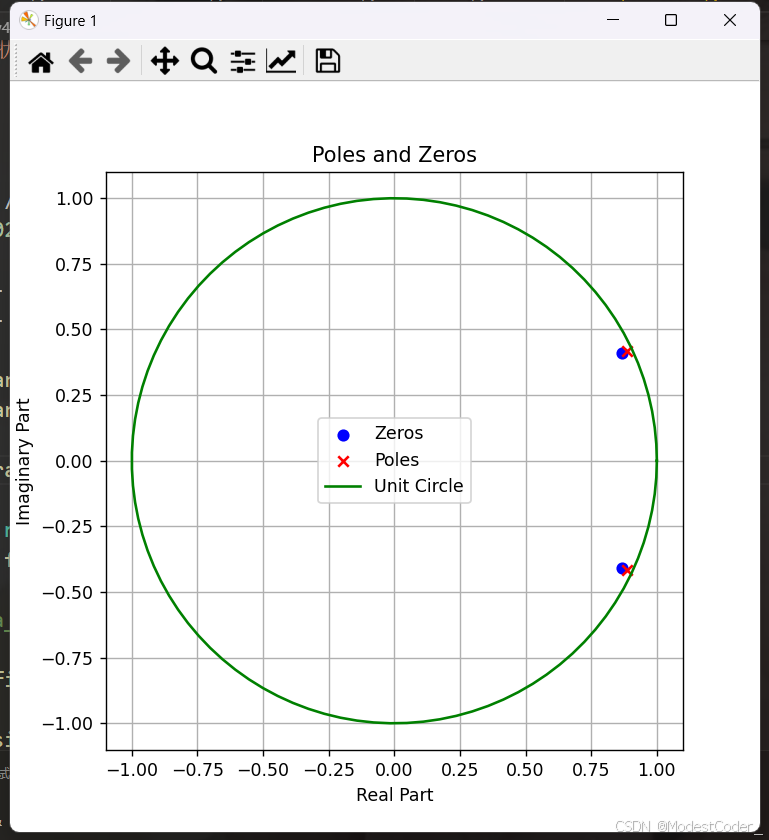
构造完了之后画一下：

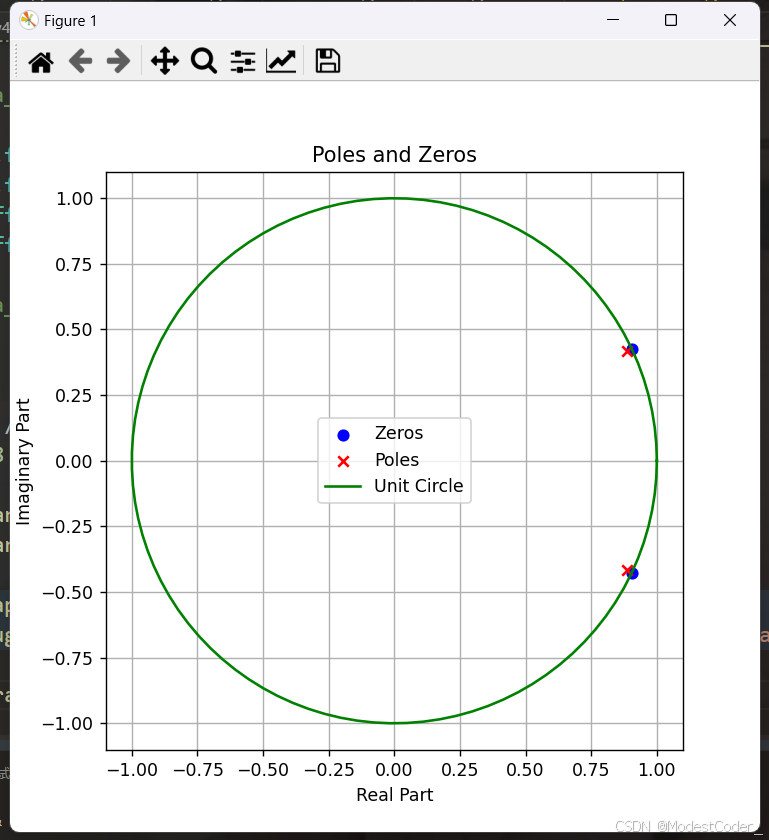
def pzmap(bz, az):
    """
    Get the poles and zeros of the filter with the given difference equation coefficients.

    ## Examples

    ```py
    bz = [2, 3]
    az = [1, -0.5]
    debug_draw_poles_and_zeros(*pzmap(bz, az))
    ```
    """
    def expand(arr, n):
        return np.pad(arr, (0, n - len(arr)), 'constant')
    m = len(bz)
    n = len(az)
    level = max(m, n)
    pad_bz = expand(bz, level)
    pad_az = expand(az, level)
    return [np.roots(pad_bz), np.roots(pad_az)]
def debug_draw_poles_and_zeros(bz, az, xlabel="Real Part", ylabel="Imaginary Part", figsize=(6, 6), title="Poles and Zeros"):

    """
    Easily plot the poles and zeros of the filter.
    """
    plt.figure(figsize=figsize)
    real_parts1 = [z.real for z in bz]
    imaginary_parts1 = [z.imag for z in bz]
    real_parts2 = [z.real for z in az]
    imaginary_parts2 = [z.imag for z in az]
    plt.scatter(real_parts1, imaginary_parts1,
                marker='o', color='b', label='Zeros')
    plt.scatter(real_parts2, imaginary_parts2,
                marker='x', color='r', label='Poles')
    theta = np.linspace(0, 2 * np.pi, 100)
    x_circle = np.cos(theta)
    y_circle = np.sin(theta)
    plt.plot(x_circle, y_circle, color='green', label='Unit Circle')
    plt.gca().set_aspect('equal', adjustable='box')
    plt.xlabel(xlabel)
    plt.ylabel(ylabel)
    plt.title(title)
    plt.legend()
    plt.grid(True)
    plt.show()

debug_draw_poles_and_zeros(*pzmap(b, a))

在这里插入图片描述

滤波器构造完成

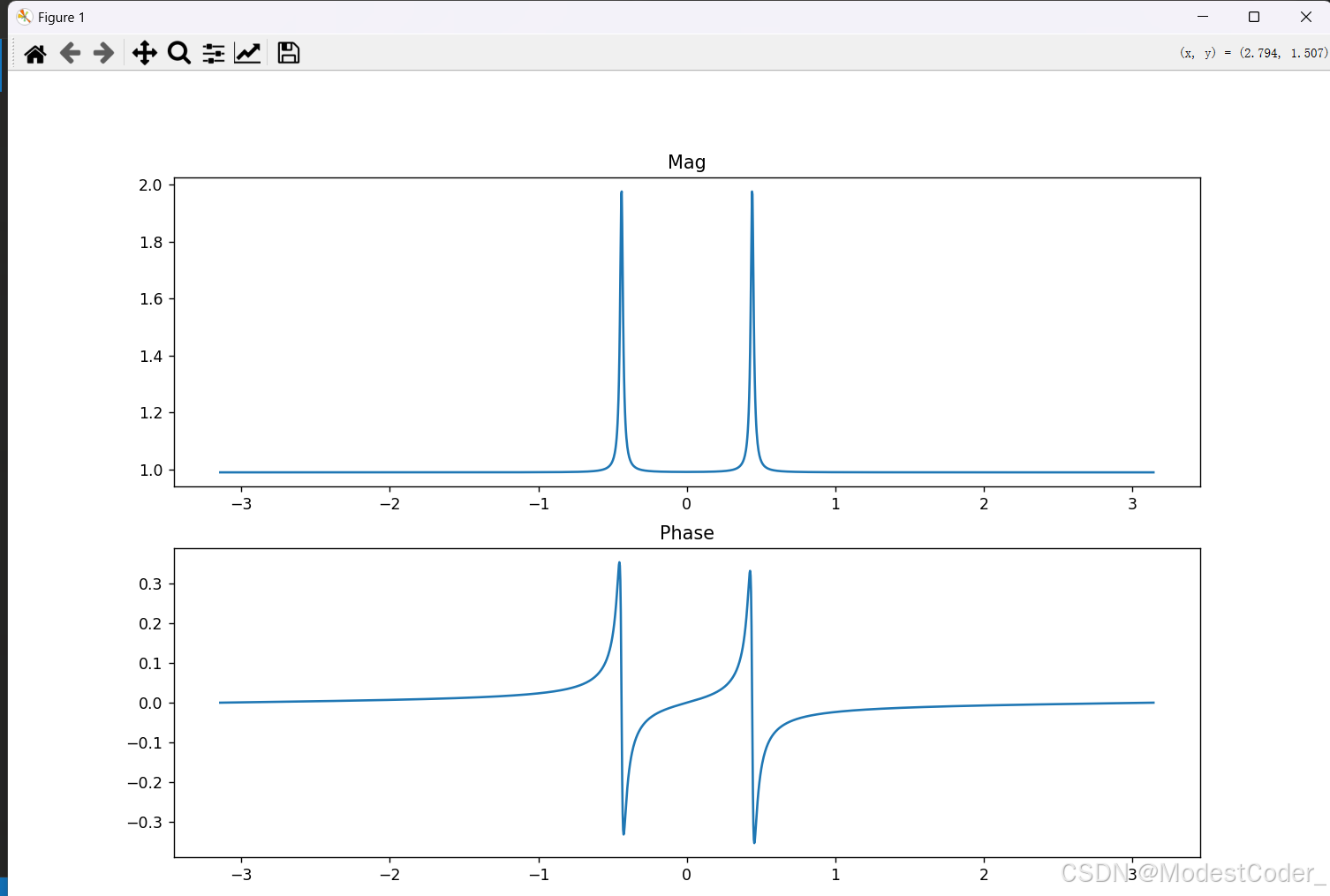
频率响应

画一个频响

w_frf = np.linspace(-pi, pi, 2000)
H_frf = freqz(b, a, w_frf)

在这里插入图片描述

滤波

把x给滤了！

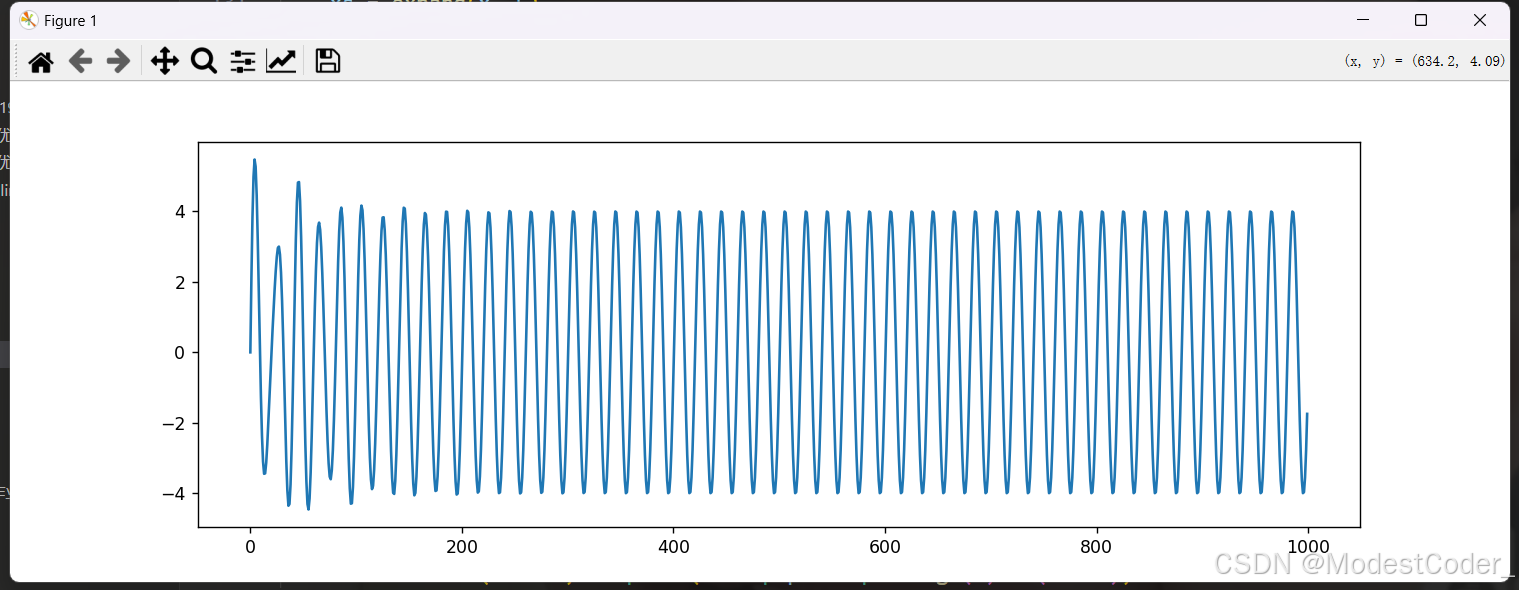
x, y = filter(b, a, x, L)

先画一下y的结果，找一下稳态部分
在这里插入图片描述

大概200~1000为稳定部分，把他取出来，加个窗

y = y[200 : 1000] * hamming_window(800)

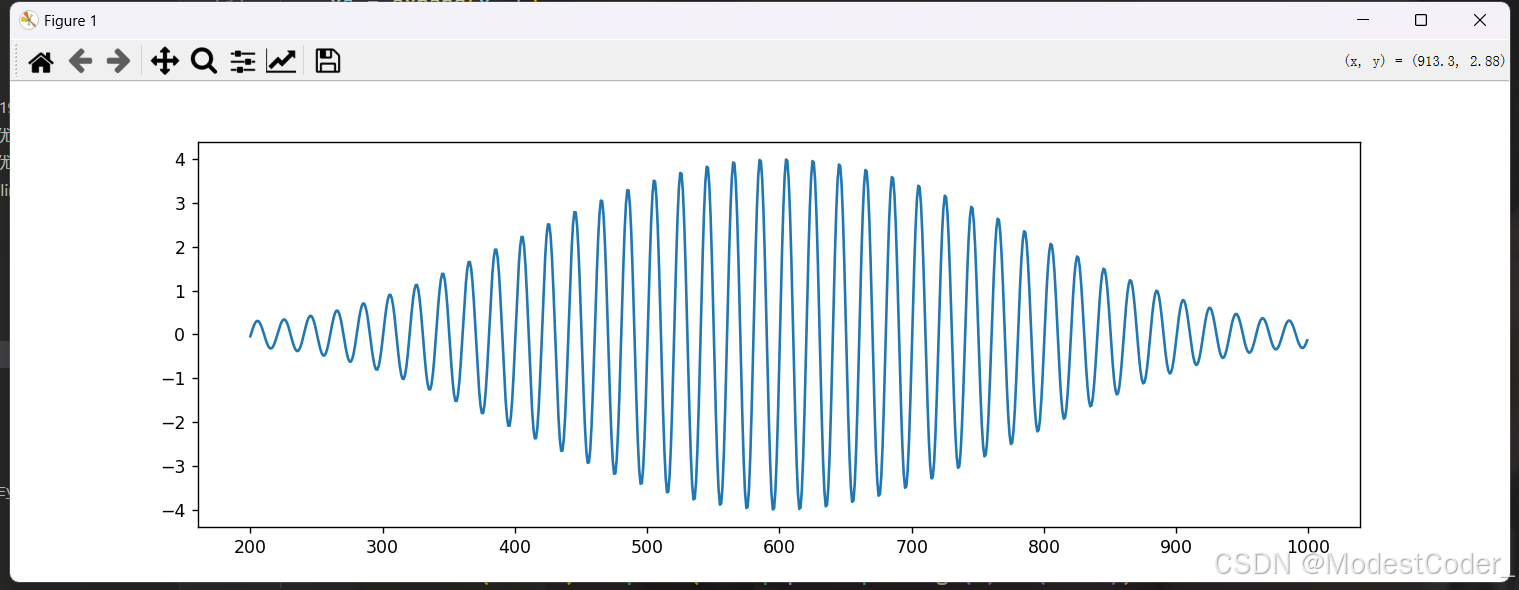
在这里插入图片描述

做FFT，查看频谱

Yw = np.fft.fft(y)
Yw = np.fft.fftshift(Yw)
w = np.fft.fftfreq(800, T)
w = np.fft.fftshift(w)

在这里插入图片描述

5.5Hz 已被滤掉

2） 梳状滤波器

再搞一个梳状滤波器

a = [1]
b = [1]
w0 = f0 / (fs / 2) * pi
dl = 0.02
K = 2
Qp = 1 - dl
Qz = 1 - dl * K

a = np.array([1, -2 * Qp * np.cos(w0), Qp ** 2])
b = np.array([1, -2 * Qz * np.cos(w0), Qz ** 2])

在这里插入图片描述
画个频响
在这里插入图片描述

滤波
x, y = filter(b, a, x, L)

先滤
然后先观察波形
在这里插入图片描述
中间挺稳定，就取200~800吧，也不想加窗了
在这里插入图片描述

Yw = np.fft.fft(y)
Yw = np.fft.fftshift(Yw)
w = np.fft.fftfreq(600, T)
w = np.fft.fftshift(w)

做一个fft

在这里插入图片描述
发现7Hz成分顺利地被乘2了！

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
【操作系统入门篇】程序员的“基础五大件”之一
台式计算机usb口不识别鼠标,如何解决计算机无法识别鼠标的问题
C++编程 拷贝(复制)构造函数 案例详细解析
Linux文件系统相关知识：存储设备、文件系统、分区、挂载、块设备、部分相关简单指令。
【水下机器人建模】基于QLearning自适应强化学习PID控制器在AUV中的应用研究（Matlab代码实现）
Qt 通过objectName得到在其他函数里生成的实例
Springboot 结合 Vue 进行本地接口联调
低照度图像增强（传统方法）
【SQL】sql语句LEFT JOIN（拼接表）详解
C语言笔记（持续更新）
;