Bootstrap

C++实现图 - 02 图的遍历（DFS、BFS）

数据结构与算法专栏 —— C++实现

写在前面：
上一讲我们对图有了一个大概的了解，但是只讲了如何存储图，还没有讲如何遍历图。这一讲我们来介绍图的遍历方式，一共分为深度优先搜索（DFS）和宽度优先搜索（BFS）。

深度优先搜索

深度优先搜索 ，简称为 DFS 。事实上，我们在树的遍历中早已涉及 DFS ，层、前序遍历、中序遍历和后序遍历都属于深度优先遍历的方式，因为这些遍历方式本质上都归结于栈。

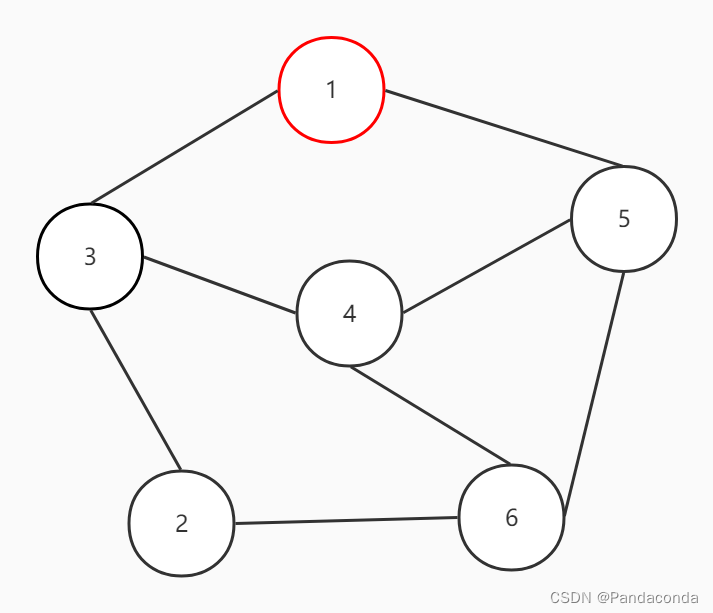
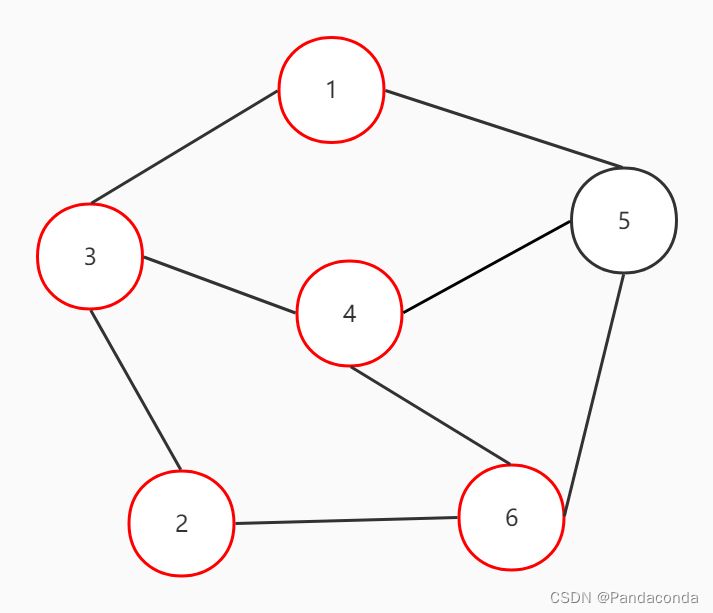
为了方便大家理解，我们还是以画图的方式来呈现（我们从结点 1 开始遍历）：
在这里插入图片描述
1、从结点 1 的第一个相邻结点即结点 2 开始遍历，先遍历哪个点一般取决于存储边的时候是以什么方式进行。
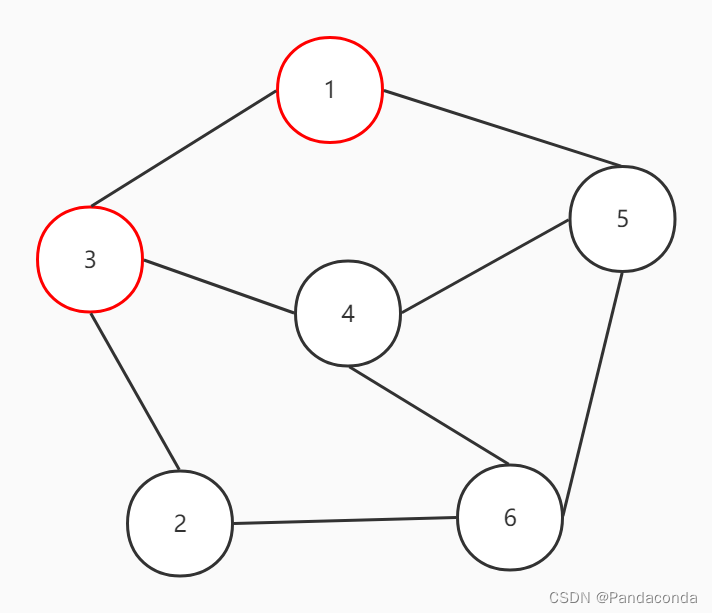
在这里插入图片描述
2、以相同的方式继续沿结点的第一个相邻结点即结点 2 遍历，就这样一直往前递归遍历直至无法继续向前。
在这里插入图片描述
3、同上，往结点 6 进行遍历。
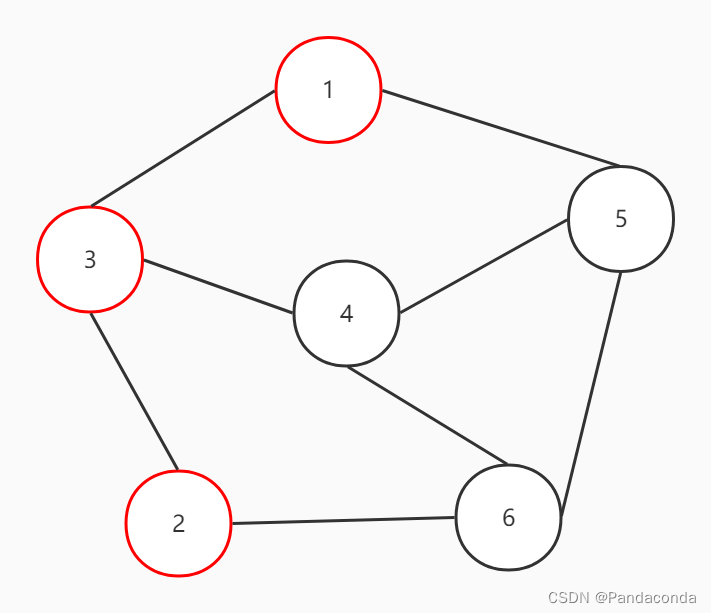
在这里插入图片描述
4、同上，往结点 4 进行遍历。
在这里插入图片描述
5、这里需要注意，结点 4 与结点 3 是相连的，所以可能会遍历到结点 3 ，但是结点 3 已经遍历过了，故直接跳到下一个结点即结点 5 进行遍历。
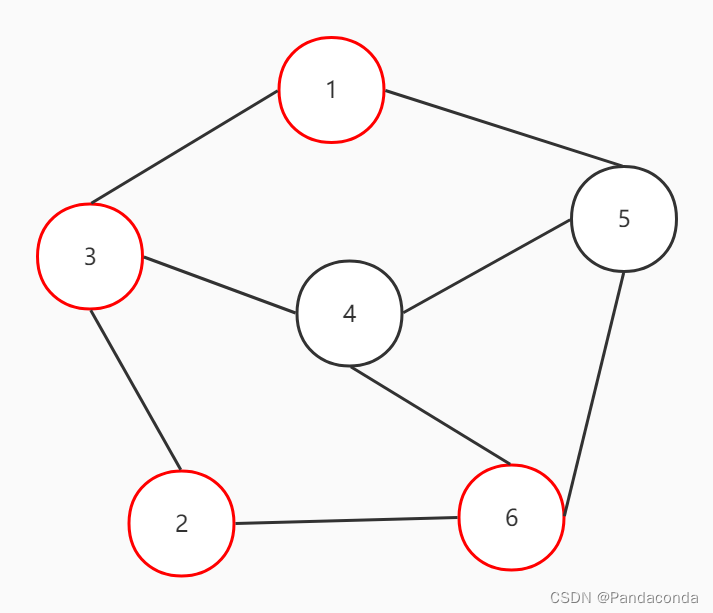
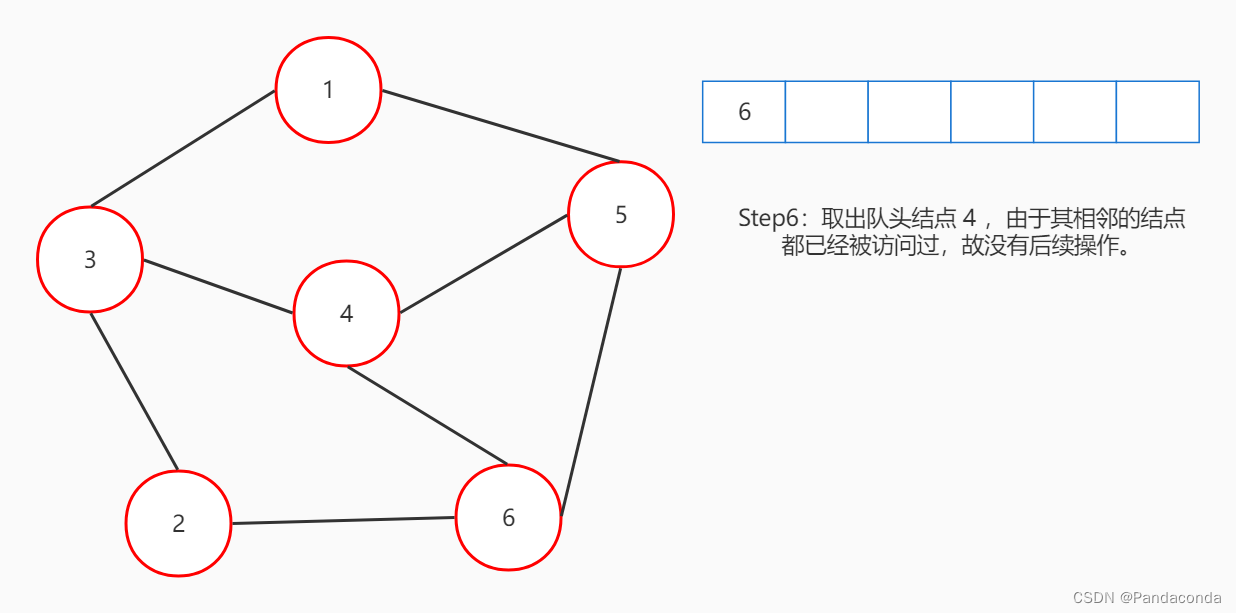
在这里插入图片描述
6、此时发现与结点 5 相邻的所有结点都已经遍历过了，故遍历结束。

其实我们通过上面的操作可以发现，深度优先搜索就是往一个方向一条路走到黑，不撞南墙不回头，没有遇到死路就不会进行回溯。

构建图

我们这里存储的是无向图，采用邻接表进行存储，还不清楚邻接表的小伙伴可以去看我上一讲的内容，这里附上传送门：

图 - 01 图的概述及实现

//定义结点
struct VertexNode
{
	int data;			//结点数据
	int weight = 0;		//边的权值
	VertexNode* next = NULL;
};

//定义图
struct GraphAdjList
{
	VertexNode* AdjList[MaxVertices];	//用邻接表存储无向图
	int numV, numE;
};

//构建图
void CreatGraph(GraphAdjList& G)
{
	int vi, vj, w;
	
	cout << "请输入顶点数：" << endl;
	cin >> G.numV;
	cout << "请输入顶点信息：" << endl;
	//初始化结点数组
	for (int i = 0; i < G.numV; i++)
	{
		cin >> vi;
		VertexNode* new_node = new VertexNode;
		new_node->data = vi;
		G.AdjList[i] = new_node;
	}
	
	cout << "请输入边的数量：" << endl;
	cin >> G.numE;
	cout << "请输入边的信息：" << endl;
	for (int i = 0; i < G.numE; i++)
	{
		cin >> vi >> vj >> w;
		//找到结点在数组中的位置，存储边 vi -> vj
		for (int j = 0; j < G.numV; j++)
		{
			if (vi == G.AdjList[j]->data)
			{
				VertexNode* temp = G.AdjList[j];
				//这里采用尾插法
				while (temp->next != NULL)
				{
					temp = temp->next;
				}
				VertexNode* newEdge = new VertexNode;
				newEdge->data = vj;
				newEdge->weight = w;
				temp->next = newEdge;
				break;
			}
		}
		
		//由于存储的是无向图，故要还要反过来存储边 vj -> vi
		int t = vi;
		vi = vj;
		vj = t;
		for (int j = 0; j < G.numV; j++)
		{
			if (vi == G.AdjList[j]->data)
			{
				VertexNode* temp = G.AdjList[j];
				while (temp->next != NULL)
				{
					temp = temp->next;
				}
				VertexNode* newEdge = new VertexNode;
				newEdge->data = vj;
				newEdge->weight = w;
				temp->next = newEdge;
				break;
			}
		}
	}
}

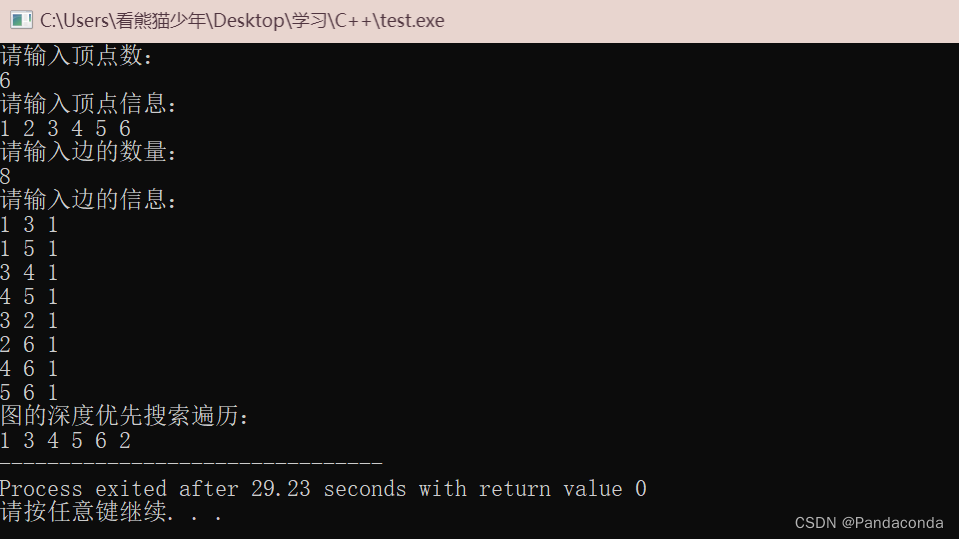
图的深度优先遍历

这里利用了两个遍历的函数，一个是主遍历一个是次遍历，因为在遍历的过程中要考虑到没有遍历全的情况，即沿着第一个结点的第一条边去遍历，结果遍历完仍有结点没有被遍历到。所以我们要对所有结点都进行深度遍历，这样就能确保所有结点都能被遍历到了。

另外需要注意的是，我在输入的时候同时输入了边的权值，但是下面代码中我没有输出它，大家可以根据情况调整想要输出的数据。

int visited[100] = { 0 };	//用来判断该结点是否有被访问过

//找到该结点在邻接表数组中的下标
int get_index(GraphAdjList& G, int key)
{
	for (int i = 0; i < G.numV; i++)
	{
		if (key == G.AdjList[i]->data)
		{
			return i;
		}
	}
}

//深度优先遍历
void DFSTraverse(GraphAdjList& G, int key)
{
	//遍历与该结点相连的每一条边
	VertexNode* temp = G.AdjList[key]->next;
	while (temp != NULL)
	{
		int vx = get_index(G, temp->data);
		if (visited[vx] == 0)
		{
			cout << temp->data << " ";
			visited[vx] = 1;
			DFSTraverse(G, vx);
		}
		temp = temp->next;
	}
}

//深度优先搜索
void DFS(GraphAdjList& G)
{
	//遍历邻接表中每一个头结点
	for (int i = 0; i < G.numV; i++)
	{
		//如果该结点没有被访问过，则遍历该结点
		if (visited[i] == 0)
		{
			visited[i] = 1;	//更新该结点状态
			cout << G.AdjList[i]->data << " ";	
			//遍历与头结点向连的每一个结点
			VertexNode* temp = G.AdjList[i]->next;
			while (temp != NULL)
			{
				int vx = get_index(G, temp->data);
				if (visited[vx] == 0)
				{
					cout << temp->data << " ";
					visited[vx] = 1;
					DFSTraverse(G, vx);
				}
				temp = temp->next;
			}
		}
	}
}

全部代码

#include<bits/stdc++.h>
using namespace std;
#define MaxVertices 100

int Size;
int maxSize = 100;

//定义结点
struct VertexNode
{
	int data;			//结点数据
	int weight = 0;		//边的权值
	VertexNode* next = NULL;
};

//定义图
struct GraphAdjList
{
	VertexNode* AdjList[MaxVertices];	//用邻接表存储无向图
	int numV, numE;
};

//构建图
void CreatGraph(GraphAdjList& G)
{
	int vi, vj, w;
	
	cout << "请输入顶点数：" << endl;
	cin >> G.numV;
	cout << "请输入顶点信息：" << endl;
	//初始化结点数组
	for (int i = 0; i < G.numV; i++)
	{
		cin >> vi;
		VertexNode* new_node = new VertexNode;
		new_node->data = vi;
		G.AdjList[i] = new_node;
	}
	
	cout << "请输入边的数量：" << endl;
	cin >> G.numE;
	cout << "请输入边的信息：" << endl;
	for (int i = 0; i < G.numE; i++)
	{
		cin >> vi >> vj >> w;
		//找到结点在数组中的位置，存储边 vi -> vj
		for (int j = 0; j < G.numV; j++)
		{
			if (vi == G.AdjList[j]->data)
			{
				VertexNode* temp = G.AdjList[j];
				//这里采用尾插法
				while (temp->next != NULL)
				{
					temp = temp->next;
				}
				VertexNode* newEdge = new VertexNode;
				newEdge->data = vj;
				newEdge->weight = w;
				temp->next = newEdge;
				break;
			}
		}
		
		//由于存储的是无向图，故要还要反过来存储边 vj -> vi
		int t = vi;
		vi = vj;
		vj = t;
		for (int j = 0; j < G.numV; j++)
		{
			if (vi == G.AdjList[j]->data)
			{
				VertexNode* temp = G.AdjList[j];
				while (temp->next != NULL)
				{
					temp = temp->next;
				}
				VertexNode* newEdge = new VertexNode;
				newEdge->data = vj;
				newEdge->weight = w;
				temp->next = newEdge;
				break;
			}
		}
	}
}

int visited[100] = { 0 };	//用来判断该结点是否有被访问过

//找到该结点在邻接表数组中的下标
int get_index(GraphAdjList& G, int key)
{
	for (int i = 0; i < G.numV; i++)
	{
		if (key == G.AdjList[i]->data)
		{
			return i;
		}
	}
}

//深度优先遍历
void DFSTraverse(GraphAdjList& G, int key)
{
	//遍历与该结点相连的每一条边
	VertexNode* temp = G.AdjList[key]->next;
	while (temp != NULL)
	{
		int vx = get_index(G, temp->data);
		if (visited[vx] == 0)
		{
			cout << temp->data << " ";
			visited[vx] = 1;
			DFSTraverse(G, vx);
		}
		temp = temp->next;
	}
}

//深度优先搜索
void DFS(GraphAdjList& G)
{
	//遍历邻接表中每一个头结点
	for (int i = 0; i < G.numV; i++)
	{
		//如果该结点没有被访问过，则遍历该结点
		if (visited[i] == 0)
		{
			visited[i] = 1;	//更新该结点状态
			cout << G.AdjList[i]->data << " ";	
			//遍历与头结点向连的每一个结点
			VertexNode* temp = G.AdjList[i]->next;
			while (temp != NULL)
			{
				int vx = get_index(G, temp->data);
				if (visited[vx] == 0)
				{
					cout << temp->data << " ";
					visited[vx] = 1;
					DFSTraverse(G, vx);
				}
				temp = temp->next;
			}
		}
	}
}

int main()
{
	GraphAdjList GA;
	CreatGraph(GA);
	DFS(GA);
	return 0;
}

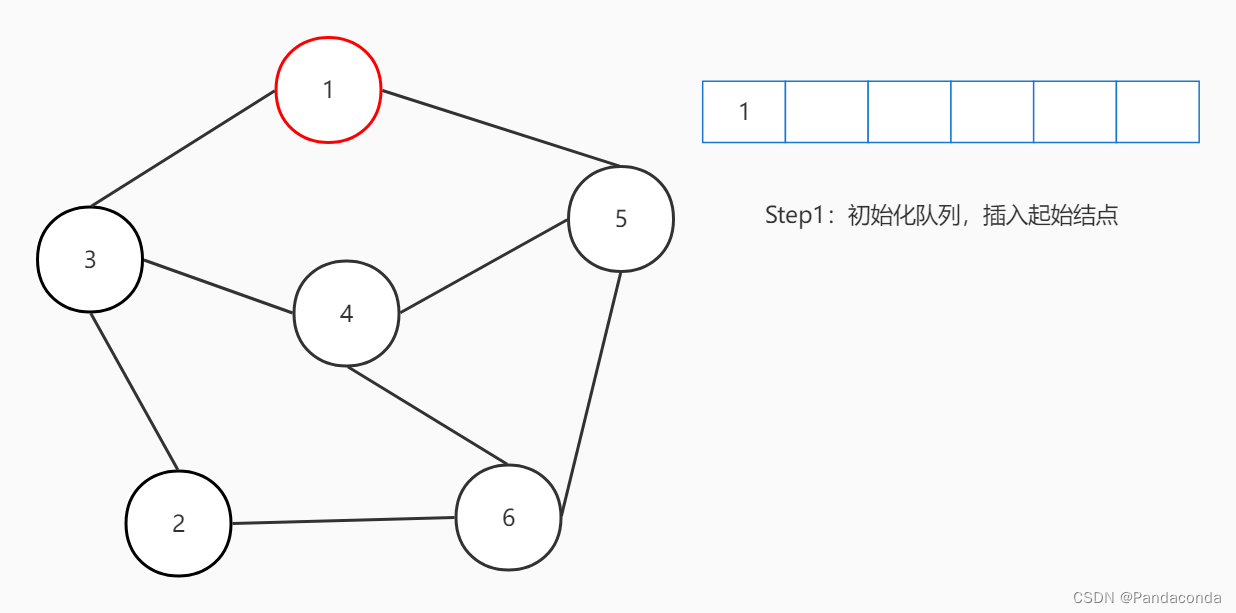
在这里插入图片描述

宽度优先搜索

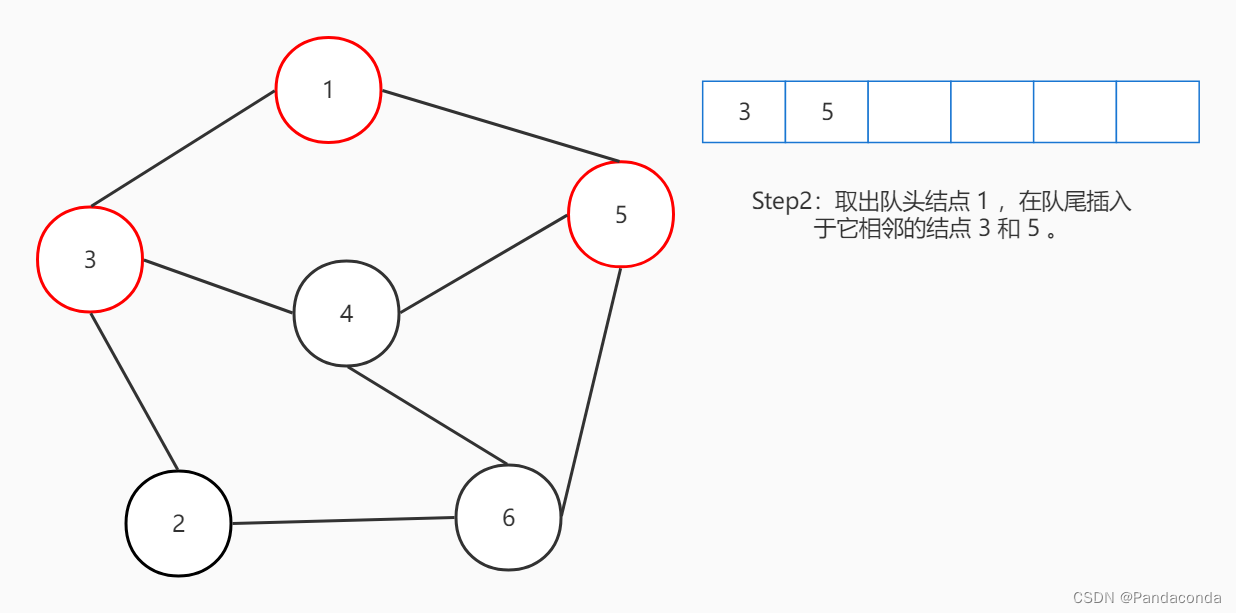
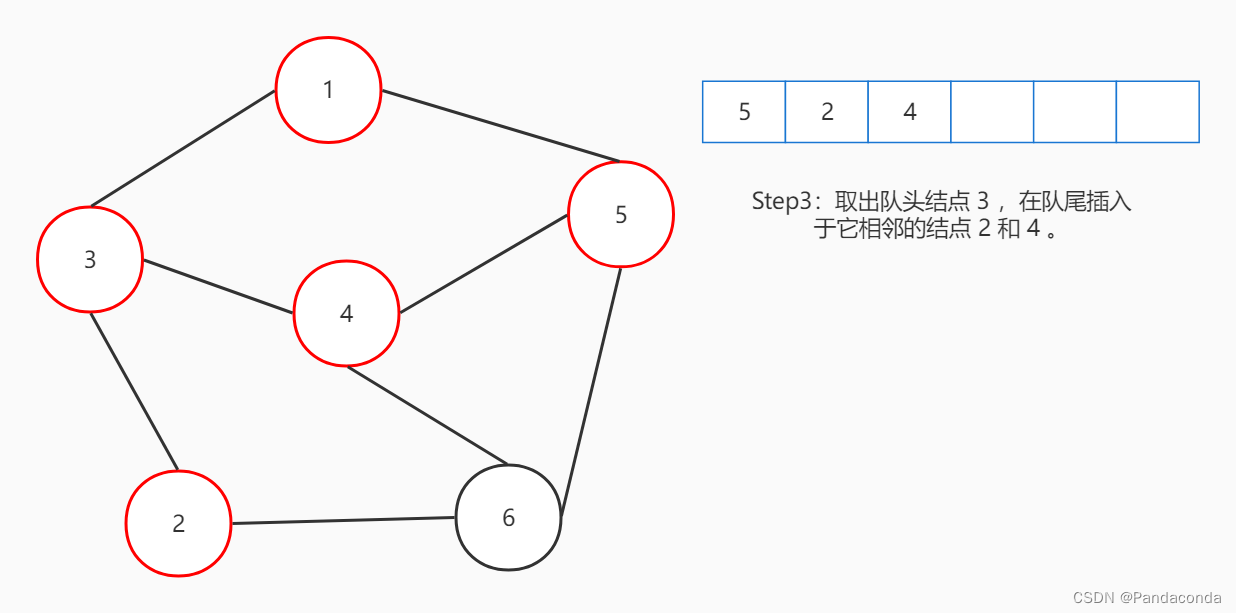
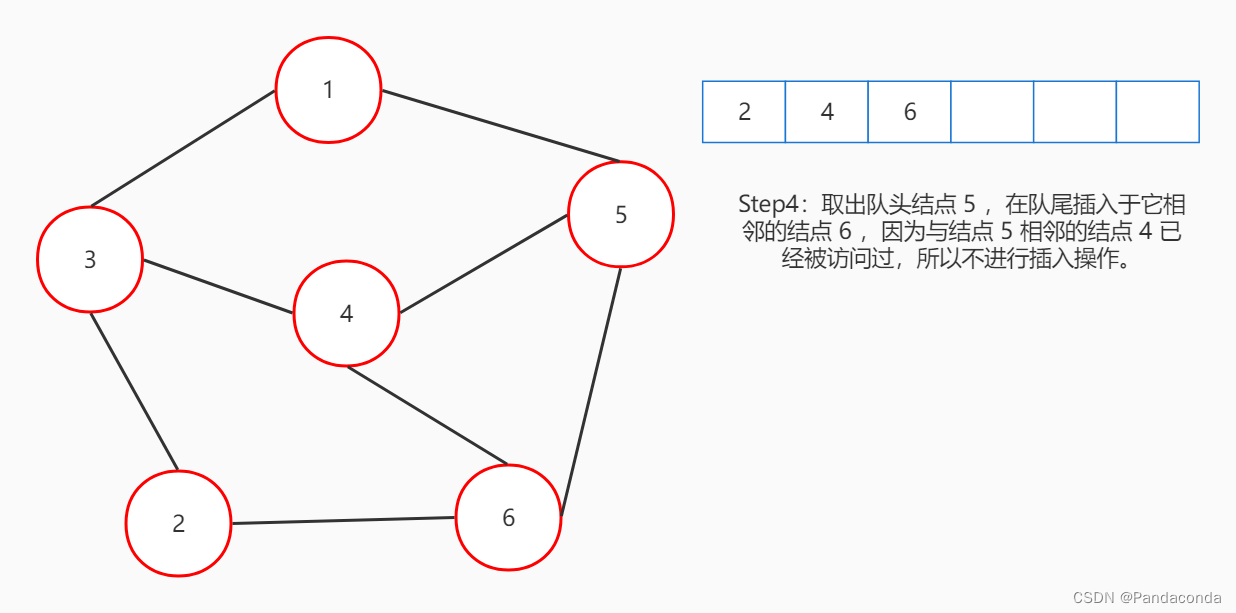
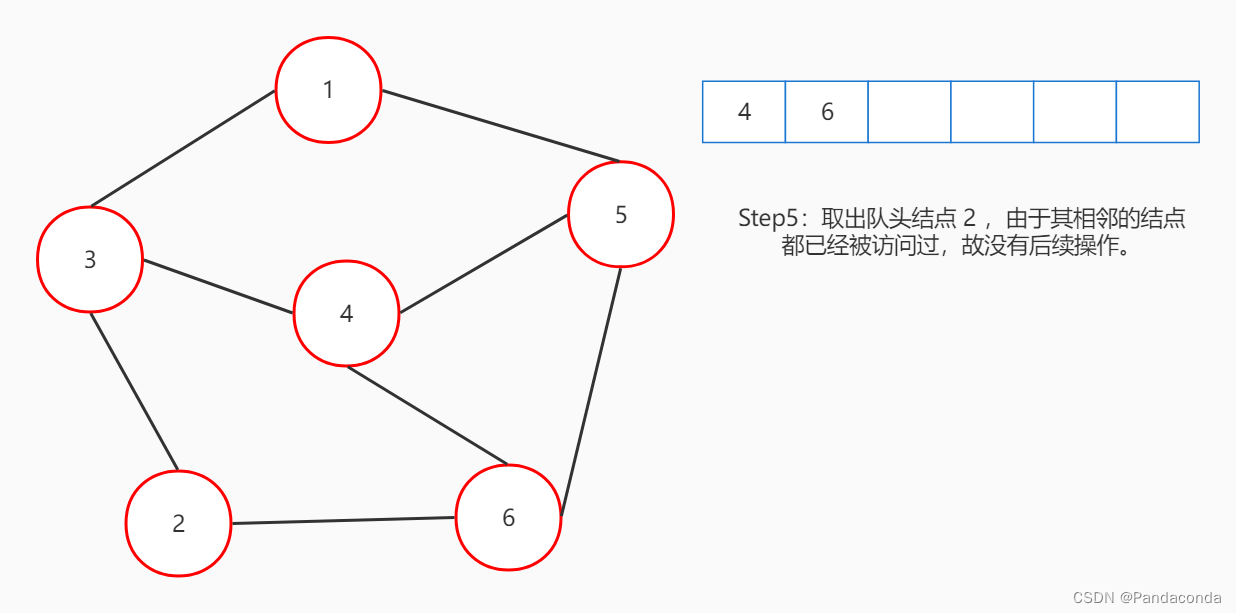
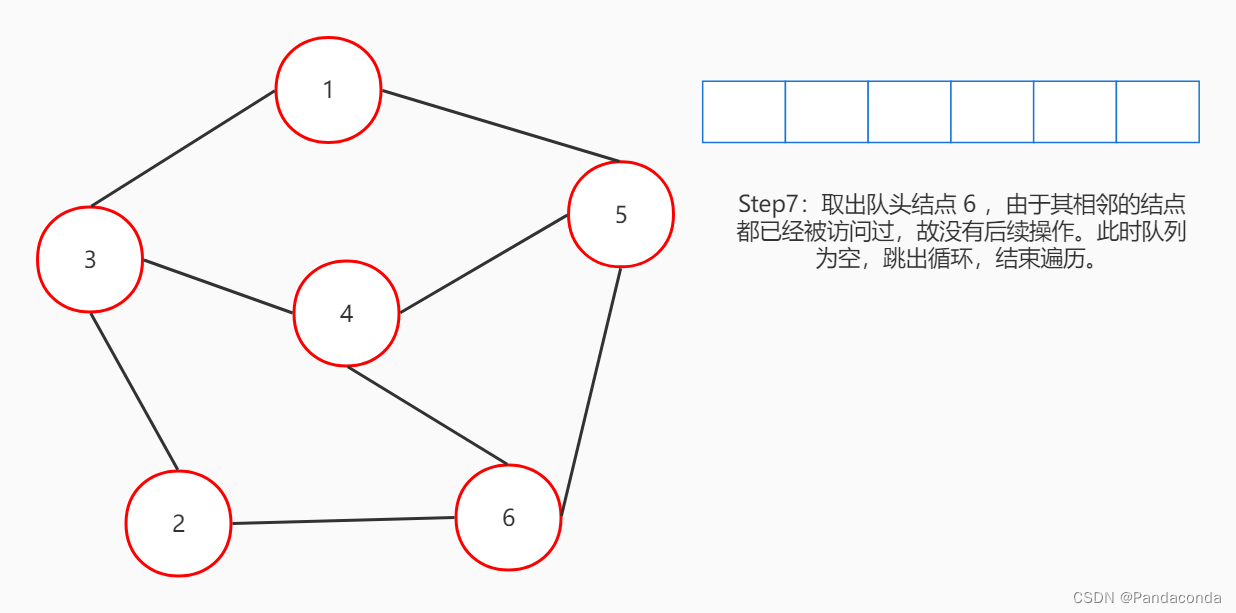
宽度优先搜索，简称 BFS 。在之前讲树的内容中，层次遍历实际上也属于宽度优先搜索。它们都用一个队列来维护元素，每次都从队头取出元素，再将与队头相邻的元素插入队尾。我们继续用图来演示：
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

构建图

宽度优先搜索我们同样可以用邻接表来存储，上面深度优先搜索我们存的是无向图，这次我们来试试有向图，比上面少了一部分操作。因为存的是有向边，所以只需要邻接表而不需要逆邻接表。由于与上面代码重复度高，所以这个部分我直接放在后面全部代码的部分了。

图的宽度优先遍历

仔细看代码可以发现，和我们层次遍历的代码有些许相似，BFS 队列的操作代码其实都是大同小异。

这里代码和上面的深搜一样没有输出权值，但是输入包含了权值，可以根据需求调整输出内容。

另外，为了方便大家更加直观的理解，我这里就没有手动实现队列了，直接调用 C++ STL 库中的 queue 。想要再复习一下手敲队列的小伙伴，可以移步到之前的文章中看看：

线性表 - 05 队列（数组实现）
线性表 - 06 队列（链表实现）

//找到该结点在邻接表数组中的下标
int get_index(GraphAdjList &G, int key) {
	for (int i = 0; i < G.numV; i++) {
		if (key == G.AdjList[i]->data) {
			return i;
		}
	}
}

//宽度优先遍历
void BFS(GraphAdjList &G) {
	int visited[100] = {0};	//用来判断该结点是否有被访问过
	queue<int> Q;	//用一个队列来保存结点

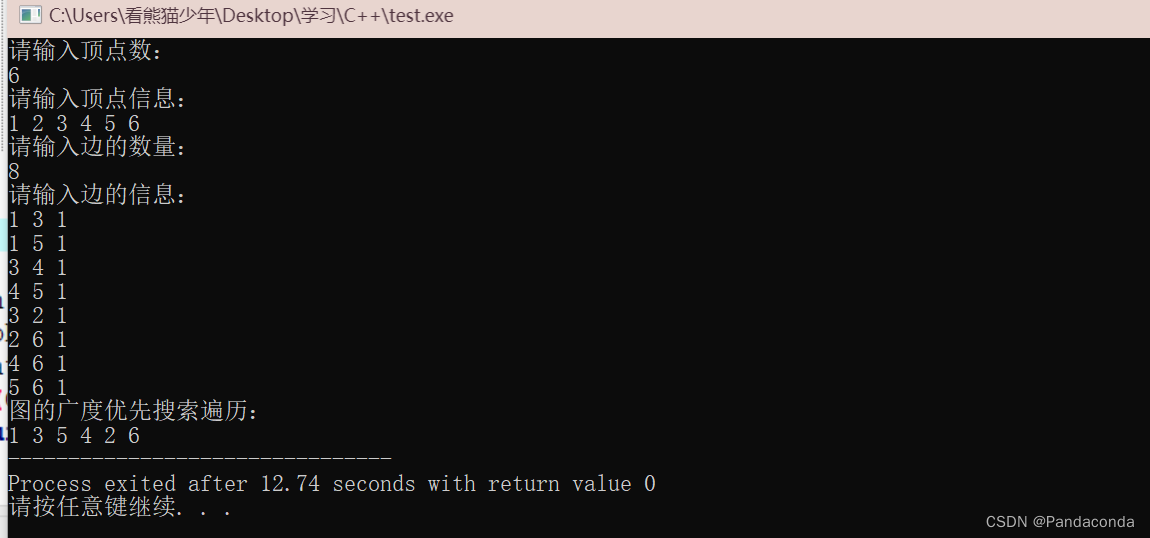
	cout << "图的广度优先搜索遍历：" << endl;
	//对每个点都进行一次BFS，考虑到图中有断边的情况
	for (int i = 0; i < G.numV; i++) {
		//如果该结点没被访问过，才继续进行操作
		if (visited[i] == 0) {
			visited[i] = 1;
			int vi = G.AdjList[i]->data;
			Q.push(vi);	//初始化队列，将起点插入队列
			//每次从队头拿出结点，再将它相邻的所有结点插入队尾，直到队列为空
			while (!Q.empty()) {
				vi = Q.front();
				Q.pop();
				cout << vi << " ";
				int vx = get_index(G, vi);
				VertexNode *temp = G.AdjList[vx]->next;
				while (temp != NULL) {
					vx = get_index(G, temp->data);
					if (visited[vx] == 0) {
						visited[vx] = 1;
						Q.push(temp->data);
					}
					temp = temp->next;
				}
			}
		}
	}
}

全部代码

#include <bits/stdc++.h>
using namespace std;
#define MaxVertices 100

//定义结点
struct VertexNode {
	int data;
	int weight = 0;
	VertexNode *next = NULL;
};

//定义图
struct GraphAdjList {
	VertexNode *AdjList[MaxVertices];	//用邻接表存储结点
	int numV, numE;
};

//构建图
void CreatGraph(GraphAdjList &G) {
	int vi, vj, w;

	cout << "请输入顶点数：" << endl;
	cin >> G.numV;
	cout << "请输入顶点信息：" << endl;
	//初始化结点数组
	for (int i = 0; i < G.numV; i++) {
		cin >> vi;
		VertexNode *new_node = new VertexNode;
		new_node->data = vi;
		G.AdjList[i] = new_node;
	}

	cout << "请输入边的数量：" << endl;
	cin >> G.numE;
	cout << "请输入边的信息：" << endl;
	for (int i = 0; i < G.numE; i++) {
		cin >> vi >> vj >> w;
		//找到结点在数组中的位置，存储边 vi -> vj
		for (int j = 0; j < G.numV; j++) {
			if (vi == G.AdjList[j]->data) {
				VertexNode *temp = G.AdjList[j];
				//这里采用尾插法
				while (temp->next != NULL) {
					temp = temp->next;
				}
				VertexNode *newEdge = new VertexNode;
				newEdge->data = vj;
				newEdge->weight = w;
				temp->next = newEdge;
				break;
			}
		}
	}
}

//找到该结点在邻接表数组中的下标
int get_index(GraphAdjList &G, int key) {
	for (int i = 0; i < G.numV; i++) {
		if (key == G.AdjList[i]->data) {
			return i;
		}
	}
}

//宽度优先遍历
void BFS(GraphAdjList &G) {
	int visited[100] = {0};	//用来判断该结点是否有被访问过
	queue<int> Q;	//用一个队列来保存结点

	cout << "图的广度优先搜索遍历：" << endl;
	//对每个点都进行一次BFS，考虑到图中有断边的情况
	for (int i = 0; i < G.numV; i++) {
		//如果该结点没被访问过，才继续进行操作
		if (visited[i] == 0) {
			visited[i] = 1;
			int vi = G.AdjList[i]->data;
			Q.push(vi);	//初始化队列，将起点插入队列
			//每次从队头拿出结点，再将它相邻的所有结点插入队尾，直到队列为空
			while (!Q.empty()) {
				vi = Q.front();
				Q.pop();
				cout << vi << " ";
				int vx = get_index(G, vi);
				VertexNode *temp = G.AdjList[vx]->next;
				while (temp != NULL) {
					vx = get_index(G, temp->data);
					if (visited[vx] == 0) {
						visited[vx] = 1;
						Q.push(temp->data);
					}
					temp = temp->next;
				}
			}
		}
	}
}

int main() {
	GraphAdjList GA;
	CreatGraph(GA);
	BFS(GA);
	return 0;
}

在这里插入图片描述

如果大家有什么问题的话，欢迎在下方评论区进行讨论哦~

【上一讲】图 - 01 图的概述及实现
【下一讲】图 - 03 最小生成树

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
Ubuntu安装mysql5.7
利用Python爬虫技术爬取京东商品评论
java基于springboot+vue的宠物用品销售商城 nodejs 前后端分离
已解决OSError: [WinError 6] 句柄无效。
解决Failed to determine a suitable driver class等bug
Au cs6怎样才能导入和导出m4a或者就是aac格式的文件呢？
MyBatis（31）MyBatis 执行查询操作时，如何避免 N+1 查询问题
matlab--pdist2(X,Y)使用方法、怎么计算的
优酷路由宝刷梅林_【荒野无灯Padavan固件】优酷路由宝L1内存卡扩展SWAP缓存+v2瑞设置详解...
CSS的background背景属性详解
;