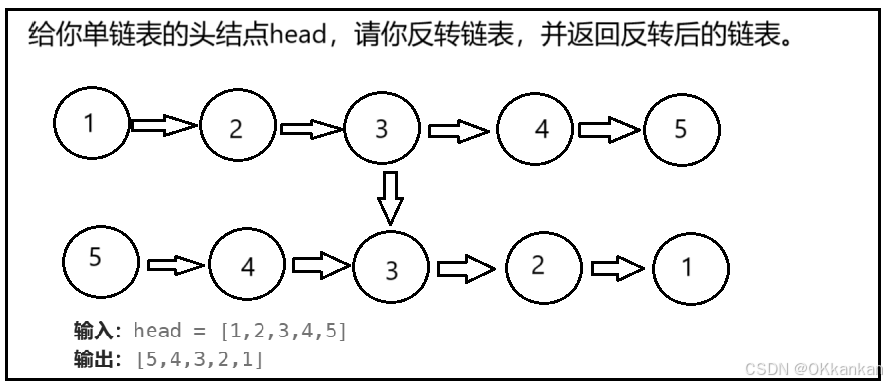
1. 反转链表
https://leetcode.cn/problems/reverse-linked-list/description/
题目:
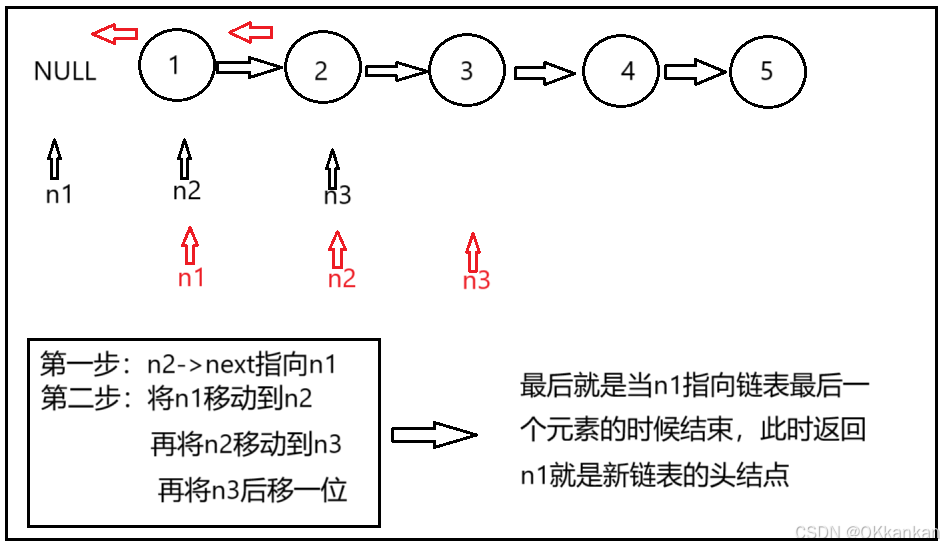
看到这个题目的时候我们怎么去想呢?如果我们反应快的话,应该可以想到我们可以从1遍历到5然后依次头插,但是其实我们还有更好的办法,就是利用三个指针,如何使用呢?
反转链表OJ
假如结构体已经给出
typedef struct ListNode SL;
SL* reverseList(SL* head)
{
//处理空链表
if (head == NULL)
{
return head;
}
else
{
//创建三个指针
SL* n1, n2, n3;
n1 = NULL, n2 = head, n3 = n2->next;
while (n2)
{
n2->next = n1;
n1 = n2;
n2 = n3;
if (n3)
{
n3 = n3->next;
}
}
return n1;
}
} 2. 链表的中间结点
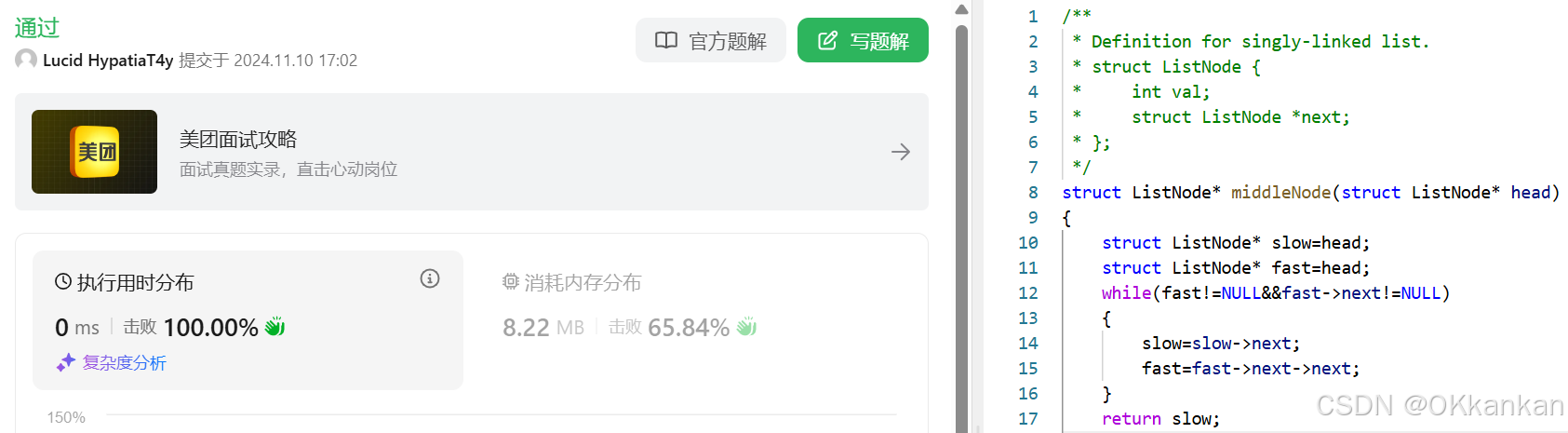
2. 链表的中间结点
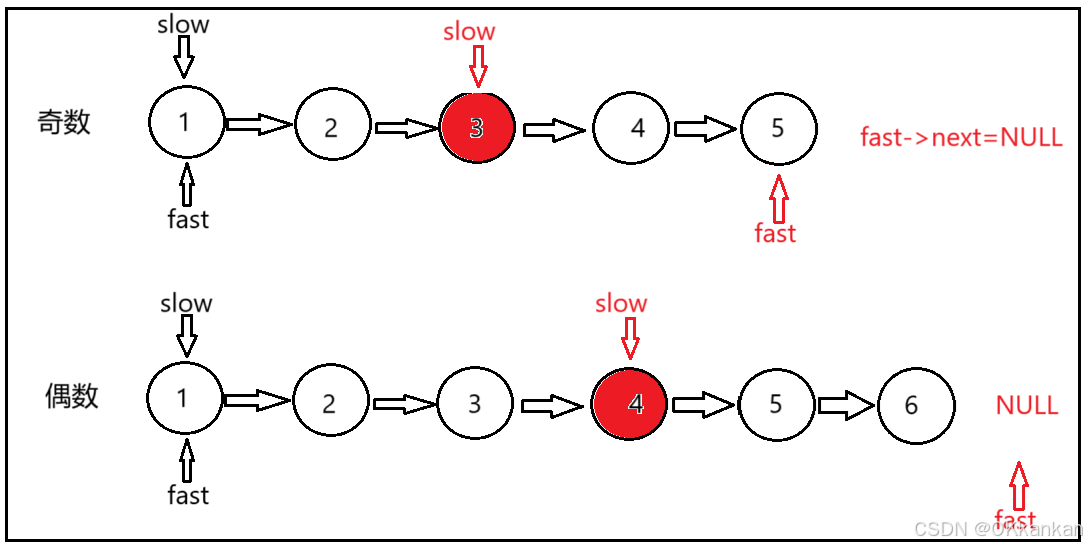
对于这个题目我们可能会想到一个简单的思路,就是遍历两边数组然后找到中间的一个结点,但是呢,今天讲一个更方便的算法叫做快慢指针,也就如上图所示,一个慢指针和一个快指针,快指针走两步慢指针走一步,最终当快指针走到终的时候慢指针刚好就在中间,让我们来实现一下:
//找链表的中间结点
//Definition for singly-linked list.
struct ListNode
{
int val;
struct ListNode *next;
};
typedef struct ListNode SL;
struct ListNode* middleNode(struct ListNode* head)
{
SL* slow = head;
SL* fast = head;
while (fast && fast->next)
{
slow = slow->next;
fast = fast->next->next;
}
return slow;
}再上一个题目中我们有一个点需要注意就是我们在写while循环的条件时候注意不能将fast&&fast->next的位置搞反,原因就是不能解引用空指针,所以顺序一定注意一下。
3. 合并两个有序链表
https://leetcode.cn/problems/merge-two-sorted-lists/description/
题目:将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。这个题目的思路也很好想出来,我们可以遍历两个升序链表,然后创建一个新的链表,将遍历的结点按升序放入新的链表中,要注意链表为空的情况。
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
typedef struct ListNode SL;
struct ListNode* mergeTwoLists(struct ListNode* list1, struct ListNode* list2)
{
//创建新的链表
SL* newhead=NULL;
SL* newtail=NULL;
//创建两个指针分别指向两个链表
SL* l1=list1;
SL* l2=list2;
//判断两个链表是否为空
if(list1==NULL)
{
return l2;
}
if(list2==NULL)
{
return l1;
}
while(l1&&l2)
{
if(l1->val<=l2->val)
{
//l1尾插到新链表中
if(newhead==NULL)
{
newhead=newtail=l1;
}
else
{
newtail->next=l1;
newtail=newtail->next;
}
l1=l1->next;
}
else
{
//l2尾插到新链表中
if(newhead==NULL)
{
newhead=newtail=l2;
}
else
{
newtail->next=l2;
newtail=newtail->next;
}
l2=l2->next;
}
}
//跳出循环有两种情况,要么l1为空,要么l2为空
if(l1)
{
newtail->next=l1;
}
if(l2)
{
newtail->next=l2;
}
return newhead;
}4. 链表的回文结构
https://www.nowcoder.com/practice/d281619e4b3e4a60a2cc66ea32855bfa
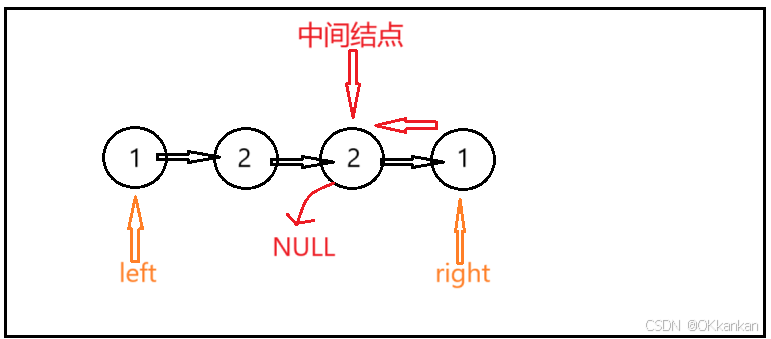
什么是回文结构?比如1221,它看起来像是对称的可以从中间重叠的感觉,叫做回文数字。像上图1->2->2->1,就是链表的回文结构。我们就是思考如何去判读一个链表是否是回文结构。我们可能会想到说这个题目需要去遍历比较是否相等,但是有一个问题就是在单链表中是不能向后遍历的,又因为这个题目是的链表长度是有限的,所以我们不妨把链表放入数组中来比较,那么如何操作呢?
/*
struct ListNode {
int val;
struct ListNode *next;
ListNode(int x) : val(x), next(NULL) {}
};*/
class PalindromeList {
public:
bool chkPalindrome(ListNode* A)
{
// write code here
//创建一个数组
int arr[900] = {0};
ListNode* pcur = A;
int i = 0;
//遍历链表,将链表中的每个结点的数值放入数组中
while(pcur)
{
arr[i++] = pcur->val;
pcur=pcur->next;
}
//找中间结点,判断是否是回文数字
int left=0;
int right=i-1;
while(left<right)
{
if(arr[left]!=arr[right])
{
return false;
}
left++;
right--;
}
return true;
}
};对于这个题目来说,它是有限制的,所以我们可以放在数组中去双向遍历,但是一旦链表没有限制,我们就不能这样来写,我们可以有另一种方法,我们的前两道题目是反转链表和找中间结点,看下面的图,如果是回文链表的话我们可以先找到中间结点,然后将其反转成为一个新的链表,再创建两个指针遍历链表,判断链表结点是否相等,最终以一个指针为NULL而结束。
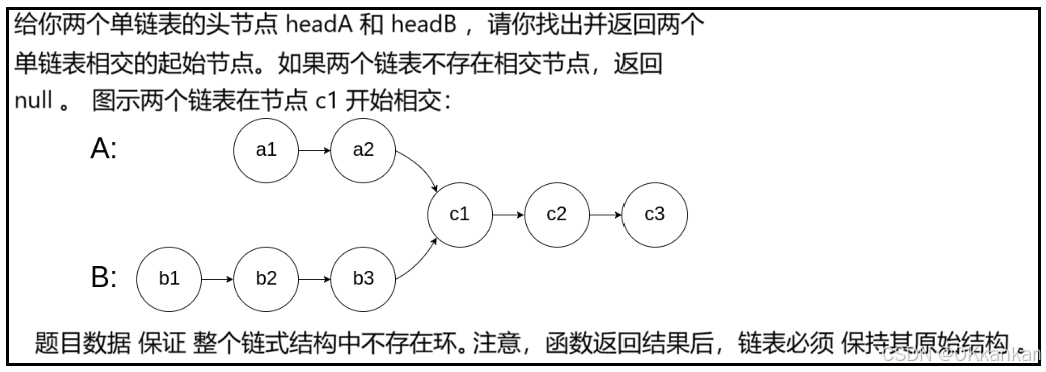
5. 相交链表
https://leetcode.cn/problems/intersection-of-two-linked-lists/description/
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
typedef struct ListNode ListNode;
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB)
{
//创建两个指针遍历链表
ListNode* l1=headA;
ListNode* l2=headB;
//先计算两个链表的长度
int sizeA=0;
int sizeB=0;
while(l1)
{
sizeA++;
l1=l1->next;
}
while(l2)
{
sizeB++;
l2=l2->next;
}//得出了两个链表的长度
//计算两数之差
int gap=abs(sizeA-sizeB);
//让长链表先走gap步
ListNode* longlist=headA;
ListNode* shortlist=headB;
if(sizeA<sizeB)
{
longlist=headB;
shortlist=headA;
}
while(gap--)
{
longlist=longlist->next;
}
//此时在同一个起点处,进行两个链表结点的比较
while(longlist&&shortlist)
{
if(longlist==shortlist)
{
return longlist;
}
longlist=longlist->next;
shortlist=shortlist->next;
}
//链表不相等
return NULL;
}6. 环形链表
https://leetcode.cn/problems/linked-list-cycle/description/
题目:给你一个链表的头节点 head ,判断链表中是否有环。如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。注意:pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。如果链表中存在环 ,则返回 true 。 否则,返回 false 。
💡 快慢指针快慢指针,即慢指针一次走一步,快指针一次走两步,两个指针从链表起始位置开始运行,如果链表带环则一定会在环中相遇,否则快指针率先走到链表的未尾。
对于这个题目我们可以使用快慢指针的方法进行解题,因为在环形链表中一个慢指针每次走一步,一个快指针每次走两步一定还会相遇,如果相遇的话那么就证明这个链表是环形链表,为什么快慢指针一定会相遇呢?当slow和fast进入环之后,此时快慢指针在环里开始进行追逐,大家会发现它们之间的距离越来越凶小,从N变成N-1变成N-2....一直到0就是指针相遇。
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
typedef struct ListNode SL;
bool hasCycle(struct ListNode *head)
{
SL* slow=head;
SL* fast=head;
while(fast&&fast->next)
{
slow=slow->next;
fast=fast->next->next;
if(slow==fast)
{
return true;
}
}
//两个指针始终没有相遇
return false;
}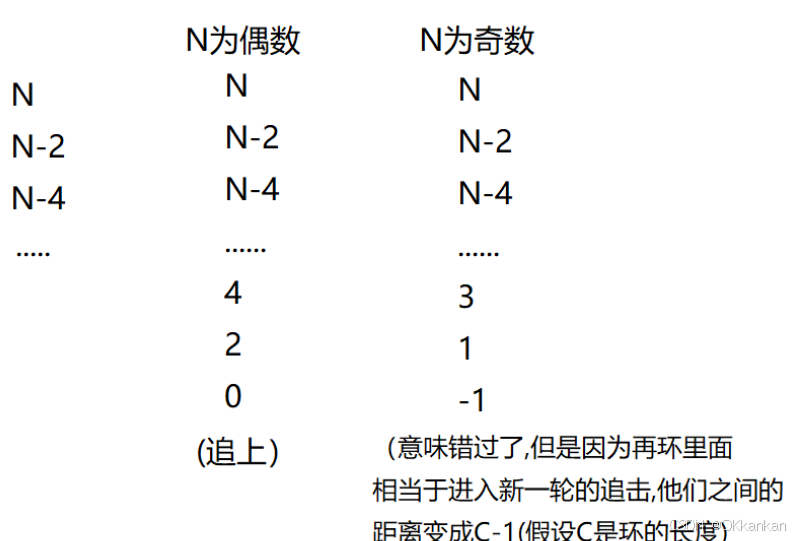
分析:1、如果N是偶数,第⼀轮就追上了2、如果 N是奇数 ,第⼀轮追不上,快追上,错过了,距离变成-1,即C-1,进⼊新的⼀轮追击a、C-1如果是偶数,那么下⼀轮就追上了b、 C-1如果是奇数, 那么就永远都追不上总结⼀下追不上的前提条件: N是奇数,C是偶数
假设:环的周长为C,头结点到slow结点的长度为L,slow走⼀步,fast走三步,当slow指针入环后,slow和fast指针在环中开始进行追逐,假设此时fast指针已经绕环x周。在追逐过程中,快慢指针相遇时所走的路径长度:fast: L+xC+C-Nslow : L由于慢指针走一步,快指针要走三步,因此得出: 3 * 慢指针路程 = 快指针路程 ,即:3 L = L + xC + C − N2 L = ( x + 1) C − N对上述公式继续分析:由于偶数乘以任何数都为偶数,因此 2L一定为偶数,则可推导出可能得情况:•情况1:偶数 = 偶数 - 偶数•情况2:偶数 = 奇数 - 奇数由step1中(1)得出的结论,如果N是偶数,则第⼀圈快慢指针就相遇了。由step1中(2)得出的结论,如果N是奇数,则fast指针和slow指针在第⼀轮的时候套圈了,开始进行下⼀轮的追逐;当N是奇数,要满足以上的公式,则 (x+1)C 必须也要为奇数,即C为奇数,满足a中的结论,则快慢指针会相遇。因此, step1 中的 N 是奇数, C 是偶数 ,既然不存在该情况,则快指针⼀次⾛3步最终⼀定也可以相遇。