LOAM代码笔记（二）

LaserOdometry
LaserOdometry的继承关系为：

BasicLaserOdometry——>LaserOdometry

LaserOdometry接收上一个节点发布的角点、平面点、_cornerPointsLessSharp、_surfacePointsLessFlat和完整的点云，将它们分别存储在_cornerPointsSharp，_surfPointsFlat，_cornerPointsLessSharp，
_surfPointsLessFlat，_laserCloud五个变量中。如果有IMU的话还会接收IMU积分出来的变换。
这个节点可以看成是一个ICP算法，对两两帧的特征点求解相对变换，主要算法位于BasicLaserOdometry::process()函数内。这里比较坑的是作者用Axis-Angle形式的旋转向量作为优化变量，用欧拉角来旋转，多了一些不必要的数据转换。

运动估计

ICP算法是求解两帧点云之间相对变换的常用算法，它的名字翻译过来就是迭代最近点，它假设两帧点云间的最近点是空间中的同一个点，通过最小化最近点之间的距离来求解位姿变换。
假设 $P_A,P_B$ 是同一个深度传感器在A,B两个位置扫描到的同一个点，传感器从A到B的变换矩阵为 $T_{AB}$ ，那么在理想状态下应满足以下方程：
$P_A-T_{AB}P_B=0$
$T_{AB}P_B$ 可以看做把 $P_B$ 投影到传感器在A处时候的坐标，而理想状态下这个坐标应与 $P_A$ 重合。
这种假设对于RGBD相机或其他能对环境进行稠密重建的传感器是行得通的，然而激光雷达的点云数据是稀疏的，我们不能保证激光雷达扫描两次一定能扫描到同一个点，哪怕是认为到这个点的距离极小。但是如果有一条边缘，或者一个平面的话，我们可以假设两次扫描都会扫到这个边缘，或者平面。那么我们就可以通过最小化当前帧某个边缘点(_cornerPointsSharp)到上一帧最近的一条边缘的距离，和当前帧平面点(_surfPointsFlat)到上一帧最近的一个平面的距离来求解相对变换。一条边缘可以两个边缘点表示，一块平面可以由三个平面点表示。
假设第k+1帧有一个边缘点 $\tilde{\textbf X}_{(k+1,i)}$ ，第k帧中离它最近的两个角点为 $\overline{\textbf X}_{(k,j)}$ ， $\overline{\textbf X}_{(k,l)}$ ，那么 $\tilde{\textbf X}_{(k+1,i)}$ 到由 $\overline{\textbf X}_{(k,j)}$ ， $\overline{\textbf X}_{(k,l)}$ 构成的边缘之间的距离为：

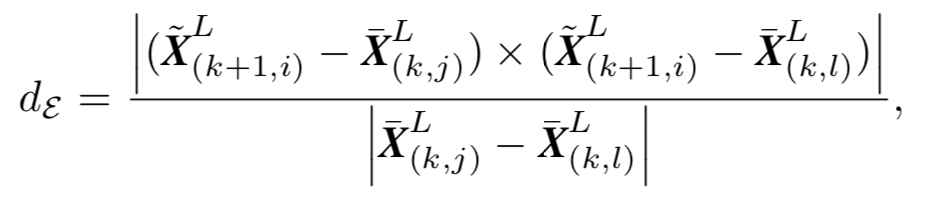
同样，假设 $(j, l, m)$ 是一小块平面上的三个点，则点到平面的距离公式为：

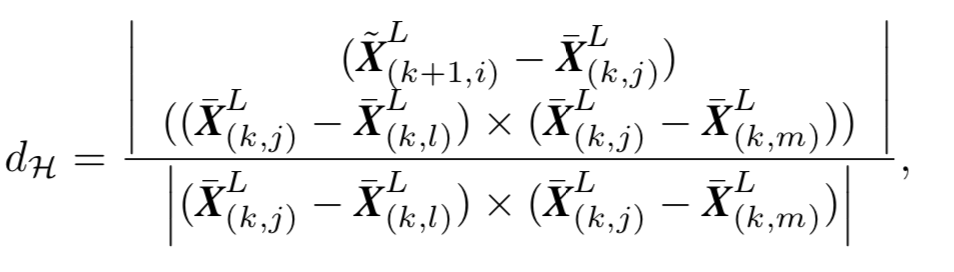
那么整个优化算法是不是就是把所有的距离项最小化就完事了呢？非也。这时候还不能保证当前帧的边缘点和平面点已经成功对应上了上一帧中的边缘和平面，每迭代若干次，都要重新用KDTree搜索最近点，然后构建新的误差项。在BasicLaserOdometry::process()函数内，每迭代5次都会重新寻找最近的边缘和平面块。

for (size_t iterCount = 0; iterCount < _maxIterations; iterCount++)
      {
         pcl::PointXYZI pointSel, pointProj, tripod1, tripod2, tripod3;
         _laserCloudOri->clear();
         _coeffSel->clear();

         for (int i = 0; i < cornerPointsSharpNum; i++)
         {
            transformToStart(_cornerPointsSharp->points[i], pointSel);//转换到开始扫描时刻

            if (iterCount % 5 == 0)
            {
               pcl::removeNaNFromPointCloud(*_lastCornerCloud, *_lastCornerCloud, indices);//去除极端数值点
               _lastCornerKDTree.nearestKSearch(pointSel, 1, pointSearchInd, pointSearchSqDis);//找到_lastCornerCloud中离pointSel最近的点
               //在_lastCornerCloud中找到离pointSel第二近的点
               int closestPointInd = -1, minPointInd2 = -1;
               if (pointSearchSqDis[0] < 25)
               {
                  closestPointInd = pointSearchInd[0];
                  int closestPointScan = int(_lastCornerCloud->points[closestPointInd].intensity);

                  float pointSqDis, minPointSqDis2 = 25;
                  for (int j = closestPointInd + 1; j < cornerPointsSharpNum; j++)
                  {
                     if (int(_lastCornerCloud->points[j].intensity) > closestPointScan + 2.5)
                     {
                        break;
                     }

                     pointSqDis = calcSquaredDiff(_lastCornerCloud->points[j], pointSel);

                     if (int(_lastCornerCloud->points[j].intensity) > closestPointScan)
                     {
                        if (pointSqDis < minPointSqDis2)
                        {
                           minPointSqDis2 = pointSqDis;
                           minPointInd2 = j;
                        }
                     }
                  }
                  for (int j = closestPointInd - 1; j >= 0; j--)
                  {
                     if (int(_lastCornerCloud->points[j].intensity) < closestPointScan - 2.5)
                     {
                        break;
                     }

                     pointSqDis = calcSquaredDiff(_lastCornerCloud->points[j], pointSel);

                     if (int(_lastCornerCloud->points[j].intensity) < closestPointScan)
                     {
                        if (pointSqDis < minPointSqDis2)
                        {
                           minPointSqDis2 = pointSqDis;
                           minPointInd2 = j;
                        }
                     }
                  }
               }
               _pointSearchCornerInd1[i] = closestPointInd;
               _pointSearchCornerInd2[i] = minPointInd2;
            }//if(iterCount % 5 == 0)
             .
             .
             .
         }
    	.
        .
        .
}

上述代码位于BasicLaserOdometry::process()内，_pointSearchCornerInd1，_pointSearchCornerInd2保存的是最近的边缘点索引，最近的平面块点的索引存放在_pointSearchSurfInd1，_pointSearchSurfInd2，_pointSearchSurfInd3内。
雅可比推导

loam的雅克比推导起来略繁琐，这里仅对部分雅可比进行详细推导。

通常情况下，我们变换一个点时通常先乘以旋转，后加平移的方式：
$\textbf p'=\textbf R\textbf p+\textbf t$
而loam在把原始点变换到开始扫描时刻的坐标时，采用的是先平移，后旋转的方式，而且采用的是按照ZXY顺序分次旋转的。令待优化变量为 $\textbf X(\theta_x,\theta_y,\theta_z,t_x,t_y,t_z)$

LOAM代码笔记（二）

悦读