作者｜郭冉、李一鹏、柳俊丞、袁进辉

常用深度学习框架的自动并行机制还不够完善，还需要用户根据经验来配置并行方式，这给开发者带来了不小的智力负担。因此，实现自动最优并行就成为一个有趣的课题。

矩阵乘是深度学习最常用的底层计算原语，譬如卷积算子，注意力机制都是通过矩阵乘来实现的，所以大规模神经网络的并行实现大多数时候也是在处理分布式矩阵乘。本文就以如何最优地实现分布式矩阵乘为例来展示自动并行的解决思路。

1

如何实现最优的分布式矩阵乘？

通过上一篇文章《手把手推导 Ring all-reduce 的数学性质》我们知道了常见集群通信操作的通信量和所需通信时间的数学性质，本文来探讨怎么使用这些性质来选择最优的并行矩阵乘策略。

在《如何超越数据并行和模型并行：从GShard 谈起》一文中，我们介绍了如何从一般的数据并行、模型并行提炼出最一般性的算子并行的抽象表示SBP。

假设我们希望在4张显卡（2台服务器，每台服务器上有2张显卡）上完成一个矩阵乘X x W=Y，也就是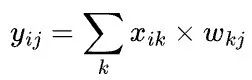，其中X和W按照特定的SBP签名被摆放（place）到4张显卡上，那么将有多个方式实现分布式矩阵乘，它们在数学上等价，不过需要调用的集群通信操作不同，从而触发的通信代价也不同。

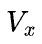
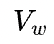
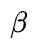
沿用《手把手推导 Ring all-reduce 的数学性质》里的符号，p表示设备数，V表示矩阵大小（表示矩阵X的大小，表示矩阵W的大小），表示传输带宽。

2

数据并行还是模型并行？

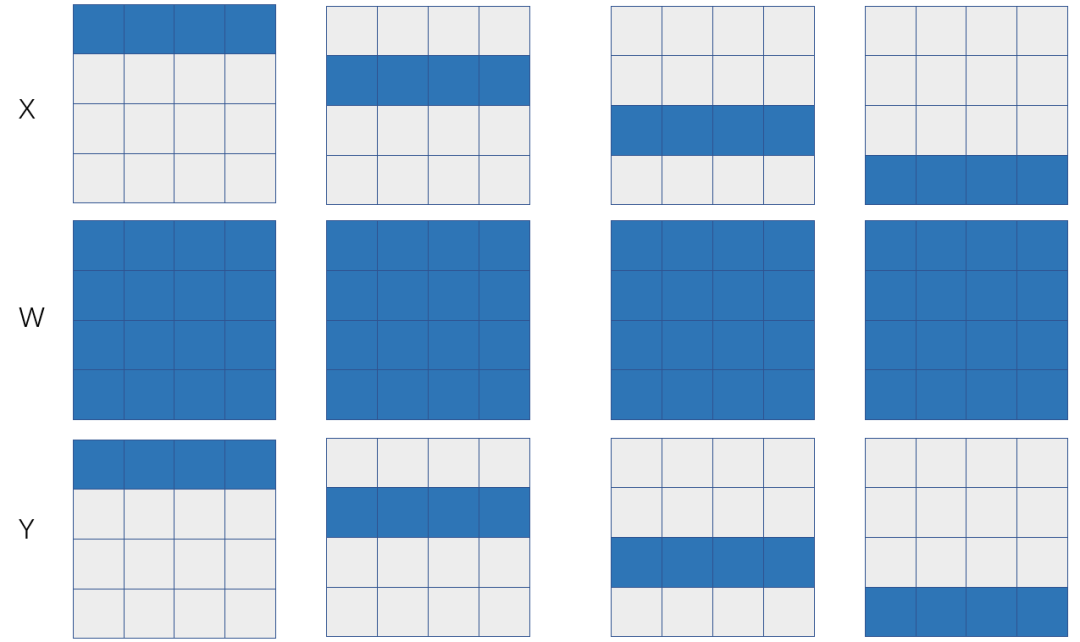
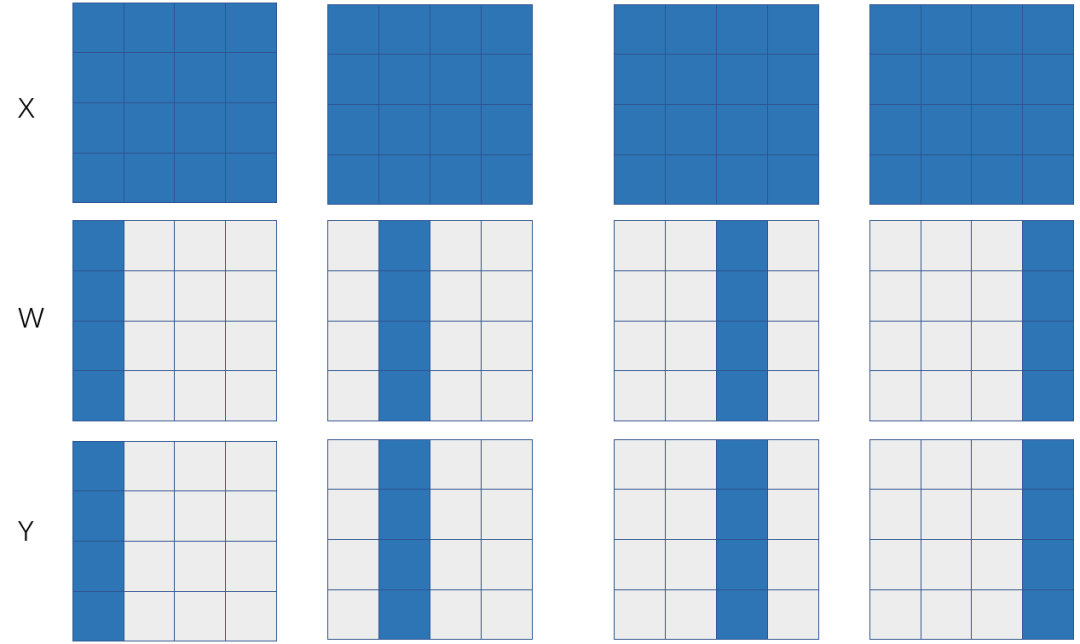
图 1：基于1D 矩阵乘的数据并行

如果‍X‍‍‍‍‍‍‍‍和W的SBP签名分别是S(0)和B，那么可以推导出来Y的SBP是S(0)，也就是左矩阵X是行划分，右矩阵W是在各个卡上是一模一样的拷贝（broadcast）。如果X表示特征数据 （feature map），W表示模型参数，那么这是一个典型的数据并行，下面我们分析一下数据‍并行的通信代价。

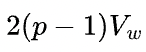
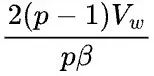
数据并行的反向需要执行集群通信操作all-reduce，如果采用环状算法，那么所有设备间的数据传输量是，执行时间是。

图 2：基于输出层神经元划分的模型并行

如果X和W的SBP签名分别是B和S(1)，那么可以推导出来Y的SBP是S(1)，也就是左矩阵X在各个卡上是一模一样的拷贝（broadcast），右矩阵W在各个卡上列划分。如果X表示特征数据 （feature map），W表示模型参数，那么这是一个典型的模型并行，下面我们分析一下这种模型并行的通信代价。

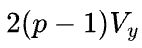
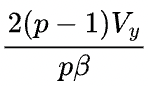
如果Y以S(1)的状态参与下游的计算，那么Y=X x W本身并不需要引入额外的通信。但假设Y需要被恢复成和X一样的状态（broadcast）参与下游计算，则前向计算时需要在S(1)签名的Y上调用all-gather操作，后向计算时需要在Y的反向error signal上调用reduce-scatter操作。那么前向和反向总的通信量是，执行时间是。

注意，矩阵乘引入的通信量不只是由当前算子决定的，还取决于它所处的上下文；这里的分析假设下游的算子需要Y保持和输入X一样的SBP签名，在这种情况下讨论不同并行方式的通信量。