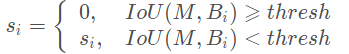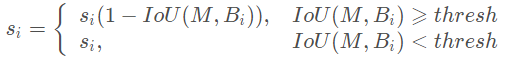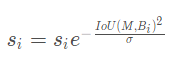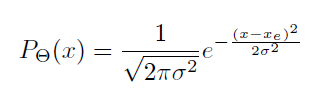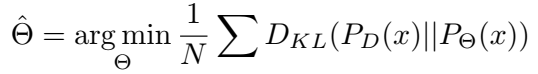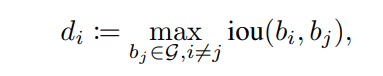一文打尽各种nms非极大值抑制

NMS（非极大抑制）

1.传统NMS（非极大抑制）

NMS即non maximum suppression即非极大抑制，顾名思义就是抑制不是极大值的元素，搜索局部的极大值。在最近几年常见的物体检测算法（包括rcnn、sppnet、fast-rcnn、faster-rcnn等）中，最终都会从一张图片中找出很多个可能是物体的矩形框，然后为每个矩形框为做类别分类概率。

以目标检测为例：目标检测的过程中在同一目标的位置上会产生大量的候选框，这些候选框相互之间可能会有重叠，此时我们需要利用非极大值抑制找到最佳的目标边界框，消除冗余的边界框。

输入格式(yolov3)：

Input:[batch_size, all_anchors, 5+num_classes]

all_anchors为所有的预测框。

5+num_classes:5的前4个参数为预测框的位置信息(x,y,w,h)，第5个参数为是不是物体的概率§。

算法流程：

非极大抑制的执行过程如下所示：
1、对所有图片进行循环。
2、找出该图片中得分大于门限函数的框。在进行重合框筛选前就进行得分的筛选可以大幅度减少框的数量。
3、判断第2步中获得的框的种类与得分。取出预测结果中框的位置与之进行堆叠。此时最后一维度里面的内容由5+num_classes变成了4+1+2，四个参数代表框的位置，一个参数代表预测框是否包含物体，两个参数分别代表种类的置信度与种类。
4、对种类进行循环，非极大抑制的作用是筛选出一定区域内属于同一种类得分最大的框，对种类进行循环可以帮助我们对每一个类分别进行非极大抑制。
5、根据得分对该种类进行从大到小排序。
6、每次取出得分最大的框，计算其与其它所有预测框的重合程度，重合程度过大的则剔除。

缺点：

(1)顺序处理的模式，计算IoU拖累了运算效率。

(2)剔除机制太严格，依据NMS阈值暴力剔除。如果两个相同物体靠得比较近，则会有两个框并且重合度非常高，通过NMS可能会剔除另一个框。

(3)具体阈值按经验选取。

(4)评判标准是IoU，即只考虑两个框的重叠面积，这对描述box重叠关系或许不够全面。

通常来看，阈值越大，代表着抑制越弱，保留的预测框数越多，极端情况下阈值为1相当于几乎没有抑制；阈值越小，代表着抑制越高，极端情况下阈值为0，对于每类只会保留一个预测框。

2.柔性非极大抑制Soft-NMS

论文：Improving Object Detection With One Line of Code（ICCV 2017）

柔性非极大抑制认为不应该直接只通过重合程度进行筛选，如图所示，很明显图片中存在两匹马，但是此时两匹马的重合程度较高，此时我们如果使用普通nms，后面那匹得分比较低的马会直接被剔除。

非极大值抑制算法NMS 存在的两个问题：

当阈值过小时，如图所示，绿色框容易被抑制；
当过大时，容易造成误检，即抑制效果不明显。

Soft-NMS认为在进行非极大抑制的时候要同时考虑得分和重合程度。

对于重合度高的预测框，NMS会直接将Score置0，即直接抑制；而Soft-NMS不会直接抑制该候选框，而是对其得分进行惩罚。

如何区分两个不同预测框是不同物体还是同种物体呢（如何设置惩罚）？若两个框是同一个物体，则IOU与Score会同时比较高，例如上图中的两个红色框。若不是同一个物体，例如红色框与绿色框，IOU不会特别高，但得分会比较高。因此对于IOU特别高的，惩罚会更大。对于NMS的剔除机制可以用下公式描述：

以下介绍几种Soft-NMS的抑制机制：

线性惩罚：

其中 M 代表当前的最大得分框。显然，IOU越大，惩罚越大。

高斯惩罚：

线性惩罚有不光滑的地方，即这种方式在略低于阈值和略高于阈值的部分，经过惩罚衰减函数后，很容易导致得分排序的顺序打乱，合理的惩罚函数应该是具有高IoU的有高的惩罚，低IoU的有低的惩罚，它们中间应该是逐渐过渡的，因此提出高斯惩罚函数。因而还有一种高斯惩罚，即：

保留机制：

NMS结束后图片集为空；而Soft-NMS依据预先设定的得分阈值来保留幸存的检测框，通常设为0.0001。

缺点：

(1)仍然是顺序处理的模式，运算效率比Traditional NMS更低。

(2)对双阶段算法友好，而在一些单阶段算法上可能失效。

(3)如果存在定位与得分不一致的情况，则可能导致定位好而得分低的框比定位差得分高的框惩罚更多(遮挡情况下)。

(4)评价标准仍是IoU，具有一定局限性。

代码：

NMS：

while detections_class.size(0):
    # 取出这一类置信度最高的，一步一步往下判断，判断重合程度是否大于nms_thres，如果是则去除掉
    max_detections.append(detections_class[0].unsqueeze(0))
    if len(detections_class) == 1:
        break
    ious = self.bbox_iou(max_detections[-1], detections_class[1:])
    detections_class = detections_class[1:][ious < nms_thres]

Soft-NMS:

while detections_class.size(0):
    # 取出这一类置信度最高的，一步一步往下判断，判断重合程度是否大于nms_thres，如果是则去除掉
    max_detections.append(detections_class[0].unsqueeze(0))
    if len(detections_class) == 1:
        break
    ious                    = self.bbox_iou(max_detections[-1], detections_class[1:])
    detections_class[1:, 4] = torch.exp(-(ious * ious) / sigma) * detections_class[1:, 4]
    detections_class        = detections_class[1:]
    detections_class        = detections_class[detections_class[:, 4] >= conf_thres]
    arg_sort                = torch.argsort(detections_class[:, 4], descending = True)
    detections_class        = detections_class[arg_sort]

3.IoU-Guided NMS

论文：Acquisition of Localization Confidence for Accurate Object Detection（2018）

链接：https://arxiv.org/pdf/1807.11590.pdf

在大部分目标检测方法中，分类和定位的处理方法是不同的。给定一个proposal，预测的每个类标签的概率就作为这个proposal的分类置信度（classification confidence），而bbox回归模块只是预测了针对该proposal的变换系数，使该proposal更接近gt box，以拟合目标的位置。在这个过程中，定位置信度（localization confidence）并没有被考虑进来，这就会带来两个缺点：

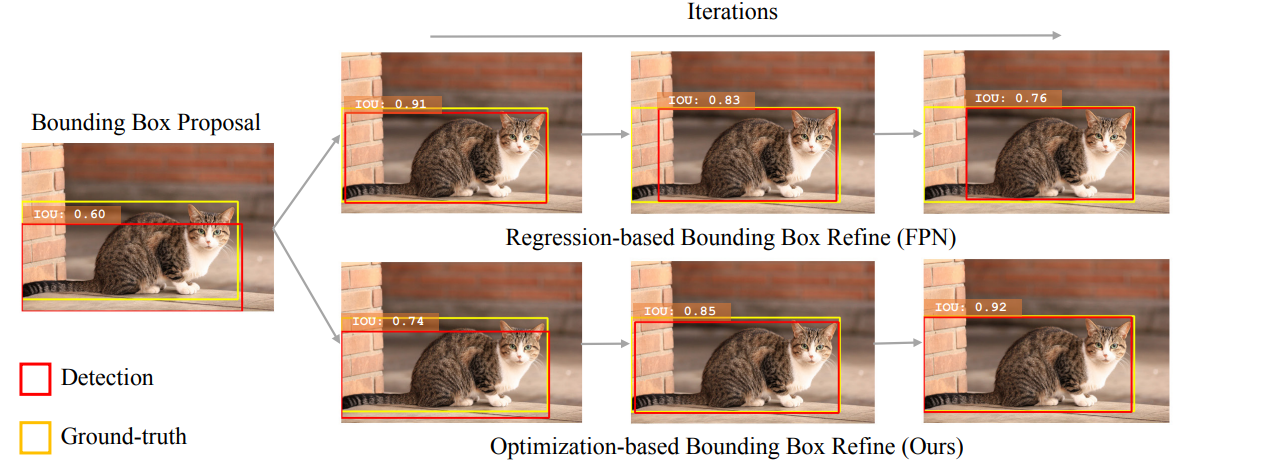
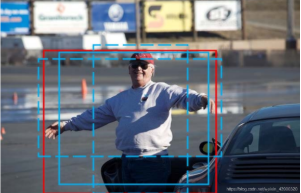
在抑制重复检测时忽略了定位精度，而只使用分类置信度对proposal进行排序。在下图中，黄色的bbox是gt，红色和绿色的bbox是检测结果，可以看到一些检测结果虽然分类置信度很高，但它们与相应的gt之间的IoU却很小。而分类置信度与定位精度之间这种不能匹配的问题，可能会导致在NMS过程中选出的是定位不准确的bbox，而过滤掉那些定位更准确的bbox。
定位置信度的缺失，可能会使得bbox回归缺少可解释性。之前的一些研究证明了bbox回归在迭代过程中的非单调性，也就是说，如果多次应用bbox回归，可能会损害输入bbox的定位效果。

对此问题作者的解决方案：

1.IOU是对定位准确度的一个天然准则。**作者用预测的IOU替换classification confidence作为NMS中的排名关键依据。**称为IOU-guided NMS，有助于消除cls conf误导下的错误。

2.提出了一种与传统的基于回归的方法表现相当的基于优化的bounding box改良流程。使用预测到的IOU优化目标，同时作为定位置信度的可解释性指示量。**提出的Precise RoI Pooling layer可以通过梯度上升求解IOU优化。**实验表明该方法能与基于CNN的检测器兼容，并且能带来定位准确率的单调上升。

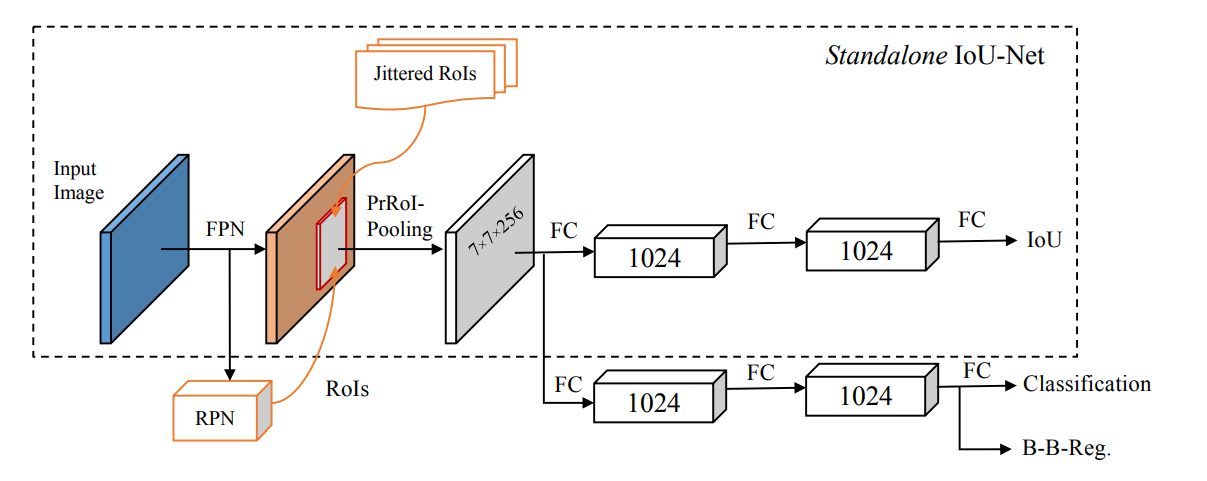
IoUNet

该文提出了IoU预测分支，来学习定位置信度，进而使用定位置信度来引导NMS。而IoU-Guided NMS即：

使用定位置信度作为NMS的筛选依据，每次迭代挑选出最大定位置信度的框 M，然后将IoU≥NMS阈值的相邻框剔除，但把冗余框及其自身的最大分类得分直接赋予M，这样一来，最终输出的框必定是同时具有最大分类得分与最大定位置信度的框。

缺点：

顺序处理的模式，运算效率与Traditional NMS相同。
需要额外添加IoU预测分支，造成计算开销。
评判标准是IoU，即只考虑两个框的重叠面积，这对描述box重叠关系或许不够全面。

4. Weight NMS

论文:Inception Single Shot MultiBox Detector for object detection (ICME Workshop 2017)

链接：https://ieeexplore.ieee.org/document/8026312/

Weighted NMS出现于ICME Workshop 2017《Inception Single Shot MultiBox Detector for object detection》一文中。论文认为Traditional NMS每次迭代所选出的最大得分框未必是精确定位的，冗余框也有可能是定位良好的。那么与直接剔除机制不同，Weighted NMS顾名思义是对坐标加权平均，加权平均的对象包括 M 自身以及IoU≥NMS阈值的相邻框。简单来说就是多框共同决定一框。

加权的权重为：

缺点：

加权因子是IoU与得分，前者只考虑两个框的重叠面积，这对描述box重叠关系或许不够全面；而后者受到定位与得分不一致问题的限制。
训练效率比传统NMS低

5. Softer-NMS

论文：Rethinking Bounding Box Regression for Accurate Object Detection（2019）

地址：https://arxiv.org/pdf/1809.08545.pdf

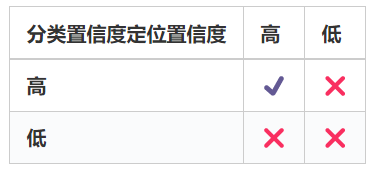
**NMS以及Soft-NMS时用到的score仅仅是分类置信度得分，不能反映Bounding box的定位精准度，既分类置信度和定位置信非正相关的。**NMS只能解决分类置信度和定位置信度都很高的，但是对其它三种类型：“分类置信度低-定位置信度低”，“分类置信度高-定位置信度低”，“分类置信度低-定位置信度高“都无法解决。

目标检测问题：

目标检测依赖于边界框回归来提高定位精度，而且通常只是直接预测出边界框偏移量，并未考虑边界框的不确定性。即存在某个目标的所有检测框都不精确问题。
边界框的不确定来通常来源于：（1）数据集标注的不确定性，如图a和图c所示。（2）遮挡所引入的不确定性：图b由于遮挡的存在，使得边界框预测的不确定性有所增加。（3）数据自身的不确定性，如图d。
类别与定位置信度不一致，例如定位精确的检测框有较低的类别分数。以此证明检测框定位置信度与类别置信度并无强相关性。

Softer-NMS的假设：

假设预测的bounding box的每个坐标都满足高斯分布：
假设ground truth bounding box是狄拉克delta分布（既标准方差为0的高斯分布极限）：

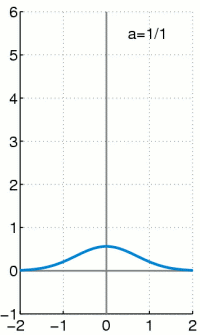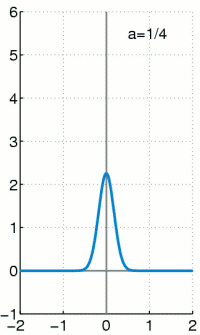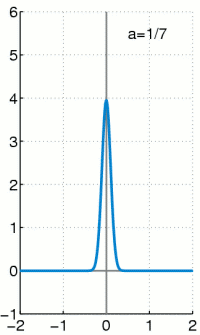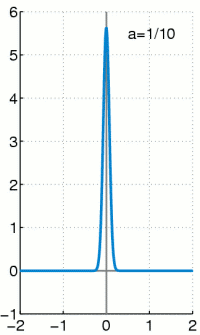
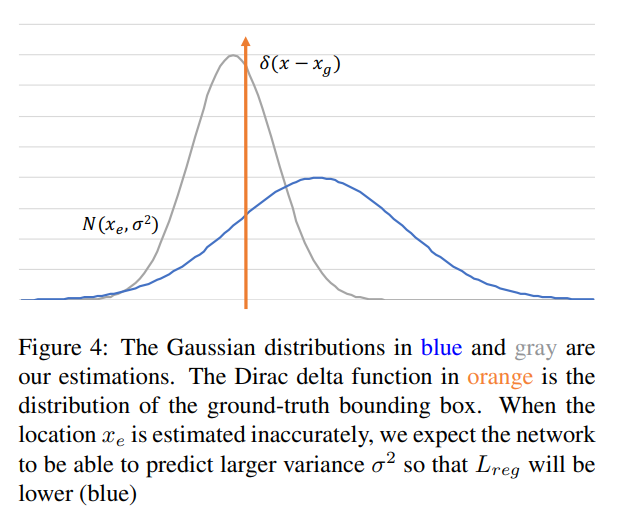
上个式子里面的delta分布是当高斯分布的σ趋于0时的极限分布，大概就是这样：

网络结构

注：其中AbsVal是一个fc层，后接绝对值层。此绝对值层是为了取代ReLU，避免σ为0。

KL 散度用来衡量两个概率分布的非对称性度量，**KL散度越接近0代表两个概率分布越相似。**上图Box std输出[N ，4]维度的向量，其中4代表bbox的各个坐标的方差。该参数使用KL Loss以期望bbox的参数分布接近于GT下bbox的参数分布。

我们估计值的高斯分布，对应蓝色和灰色的曲线。橙色的曲线是ground-truth对应的狄拉克函数。当预测bbox位置没被估计准确，我们期望预测结果有更大的方差，这样Lreg会比较低（蓝色）。

KL Loss:

边界框回归的目标是令边界框的理论分布去拟合真实分布，用KL散度来度量这两个分布的差异程度，即：

因此，可使用KL loss作为边界框回归损失：

忽略常数项，得到：

可以看出，当σ=1，KL loss退化成L2loss：

分别对和σ求导得：

由于σ在分母，在训练初期σ 很小，所以可能会出现梯度爆炸，所以不能令网络直接输出σ，重新调整网络输出为，此时损失函数为：

在测试阶段，将网络输出的α重新转换成σ。
另外，为减小该损失函数对于异常点的敏感性，借助Smooth L1 loss，当时，令：

是真实标签，α 由新添加的网络分支得到，那么从哪来呢？实际上就是原来的回归分支所输出的坐标偏移量的预测值经过转化后得到的预测坐标。从概率论的角度讲，一个随机事件得到某个结果，那么该结果对应的概率是最大的。而高斯分布中，均值出对应的概率是最大的，所以把输出坐标作为高斯分布的均值是合理的，这也是只需要新添加一个标准差分支的原因。

Variance Voting：

目前已经得到边界框定位的不确定性，如何使用这种不确定性来调整边界框，成为接下来所要研究的重点问题。边界框的不确定性处理影响自身的定位，由于NMS的存在，还会影响附近其它边界框的定位，所以在进行NMS时，应考虑这种不确定性带来的影响。
假设网络共输出：N个边界框，N个边界框的分数，N个边界框的方差
假设在soft-NMS的某一轮迭代中分数最高的边界框为

则该边界框的某个坐标会根据以下3个方面来重新调整：

（1）自身的不确定性
（2）附近其它边界框与该边界框的IoU
（3）附近其它边界框的不确定性。
调整后的新坐标为：

其中，是可调参数。由上述公式可知，附近其它边界框指与目标边界框b有重叠区域(IoU＞0）的边界框。

表示各个边界框（目标边界框+附近其它边界框)对目标边界框的影响程度。
根据这些边界框与目标边界框的IoU大小计算，就是soft-NMS中提出的高斯re-scoring function，重叠面积越大，越大，附近边界框对目标边界框的影响也越大。
当时，IoU=1，=1，此时表示自身的不确定性，不确定性越大，则新坐标受原坐标的影响越小，而受其它边界框的影响就越大。
其它边界框的越小，对目标边界框的影响就越大。
如果预测得不准确，此时应该让不确定性更大，loss会增加。

算法流程：

加权平均法合并边界框：对于每一个M，作者通过对它附近的边界框（IOU>N_t）及它自身取加权平均来回归出更为精确的框。 x是参数化之后的偏移量：

简单来说，Softer-NMS同样是坐标加权平均的思想，不同在于权重 wi发生变化，以及引入了box边界的不确定度，而加权公式如下：

6.Adaptive NMS

论文：Adaptive NMS: Refining Pedestrian Detection in a Crowd（CVPR2019)

链接：https://arxiv.org/abs/1904.03629

Soft-NMS可以通过施加惩罚来抑制那些与IoU比较大并且预测同样物体的框，但如果两个物体十分接近从而导致预测不同物体的两个框也有很大的IoU，Soft-NMS仍会抑制掉，Soft-NMS不能解决这个问题。但是回想一下，NMS的threshold越高，抑制越小；threshold越小，抑制越大，因此我们可以让人群密集的地方，NMS阈值较大，而人群稀疏的地方NMS阈值较小。但是问题在于怎么判断人群是否密集，又怎么根据密集程度定NMS阈值呢？于是就引入了CNN。

在Adaptive NMS中，想结合Soft-NMS，从而达到在人群密集处减少惩罚，在人群稀疏处增大惩罚。

密度定义

di表示对物体i的稠密程度。i表示每个生成的候选框bbox，j表示真实标注的框。

阈值定义

其中Nm为Adaptive NMS的threshold，dM为密度。这里虽然惩罚了重叠的bbox，使得其置信度分数降低。但是，提高了阈值，假设密度得分高于Nt阈值，则正式的NMS阈值将加大，选择没有那么重叠的bbox不进行惩罚，从而提高了高遮挡下bbox的保留。

算法流程

其中Greedy-NMS代表普通的NMS。

密度预测模块

论文把，密度预测作为一个回归任务，密度的值采用上述定义计算，损失函数为Smooth-L1 loss。

在训练CNN时，每次还需要求出密度作为监督信号，训练网络能够拟合这个密度函数，即输入一张图片，能输出每个位置的物体密度。