机器学习与scikit-learn（一）——回归模型

作者：CUG_UESTC
出处：http://blog.csdn.net/qq_31192383/article/details/78723468

本博客主要是为了将一些常用的方法进行一个总结，之前许多方法都只是一知半解，也没有实现过。这次刚好想学习scikit-learn，所以顺便复习一下机器学习相关方法，结合理论加实践的方法。

安装

一般来说如果用Anaconda安装的python环境的话，会自带sklearn包。安装这里没什么好说的，详情参考：安装教程

线性回归

一元线性回归
线性回归是机器学习中最简单的模型，但是要知道许多复杂的模型都是从线性模型演化而来，其思想都是一脉相承的。所以我们先从线性回归模型入手进行学习。
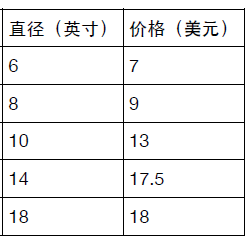
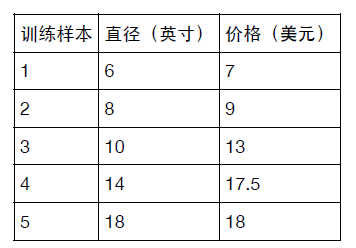
生活中有一些问题是可以通过线性模型来解释的，譬如，我们有如下数据：

表示不同尺寸的披萨所对于的价格，可以很清楚的看到，披萨的尺寸越大，其价格呈线性增长。
线性回归模型主要学习具有如下形式的函数参数
$(1)f(x) = w_1x_1+w_2x_2+...+...w_dx_d+b$
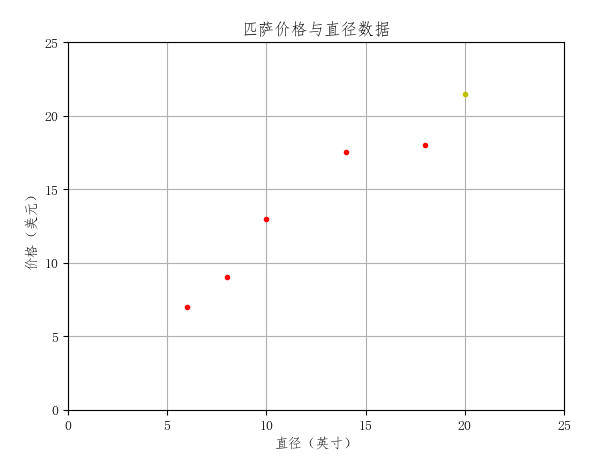
其中的 $w_i$ 和 $b$ 就是模型的参数，通过大量的数据可以学习到这些参数。参数一旦确定之后，对于一个模型从未见过的数据，好比上面的例子中问你尺寸为20的披萨多少钱，模型就可以基于现有数据所存在的规律，预测出一个结果。
```
#对于上述的例子，我们可以通过一个简单的例子了解一元线性回归和sklearn的基本使用


#-*-coding:utf-8-*-

import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
import numpy as np


#定义绘图格式

def runplt():
    plt.figure()
    plt.title('匹萨价格与直径数据')
    plt.xlabel('直径（英寸）')
    plt.ylabel('价格（美元）')
    plt.axis([0, 25, 0, 25])
    plt.grid(True)
    return plt
plt = runplt()


#表格中的数据

X = [[6], [8], [10], [14], [18]]
Y = [[7], [9], [13], [17.5], [18]]
plt.plot(X, Y, 'r.')

#创建一个线性回归模型

model = LinearRegression()

#将训练数据喂给模型并训练

model.fit(X, Y)

#测试披萨的尺寸大小

test = 20

#调用已训练的模型进行预测

pre = model.predict(test)
plt.plot(test, pre, 'y.')
print(pre[0][0])
plt.show()
```
代码的结果如图：

图中红点代表训练数据，黄色的点为预测结果。
上述例子其实是一个一元回归模型，因为它只有披萨的尺寸这一个影响价格的属性，因此式子(1)可以改写为下面这个式子：
(2) $y=\alpha+\beta{x}$
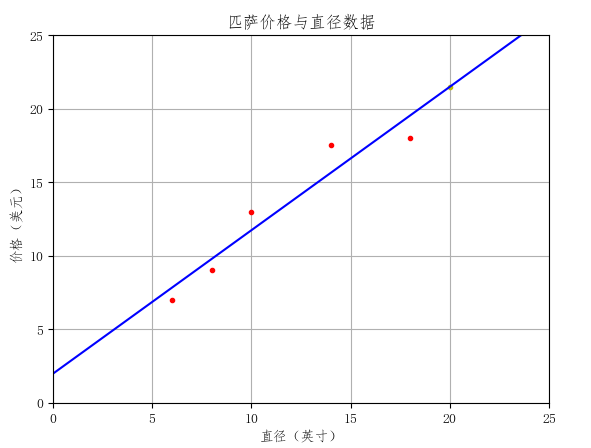
也就是上面代码中的model学习的是这里的 $\alpha和\beta$ 。这其实就是一条直线：
```
#将上面最后一行代码注释掉

test = [[0], [25]]
pre = model.predict(test)
plt.plot(test, pre, 'b-')
plt.show()
```
可以看到其结果是一条直线。
至此，可以看到一元线性回归是很容易实现的，那它是如何学习到上面的参数的呢？
带成本函数的模型拟合评估
上述参数其实满足一条性质，那就是对所给的训练集，使其成本函数也就是损失函数最小，这里损失函数在机器学习领域有很多，对于线性回归，我们一般使用均方误差来作为损失函数，使得均方误差最小的参数即我们所需要的解。
在给出参数的求解公式之前，我们通过numpy内置的最小二乘的函数，对上表中的数据进行拟合，并预测披萨尺寸为20时的价格：

#在上面的代码后面添加如下代码手动求取最小二乘
from numpy.linalg import lstsq
X = [6, 8, 10, 14, 18]
X = np.vstack([X, np.ones(len(X))]).T
w, b = lstsq(X, Y)[0]
#输出参数
print(w, b)
pre = w * 20 + b
print(pre)
#输出结果和上面使用sklearn内置线性回归模型结果一样

  可以看到通过lstsq函数求出了参数$w和b$(即(2)中的$\alpha和\beta$)。然后通过公式(2)带入$x=20$解出$y$。
为了统一，我们先给出多元线性回归的表达式，再统一用矩阵的格式统一给出参数求解公式，其实一个数可以看作一个1X1矩阵。

多元线性回归
多元线性回归即具有式子(1)那样的表示形式， $(f(x) = w_1x_1+w_2x_2+...+...w_dx_d+b$ ，可以看到这时，预测值 $f(x)$ 不仅仅与一个 $x$ 有关，而是 $d$ 个 $x$ 同时决定。但是每个 $x$ 对最后结果的决定性分量是不一样的。写成矩阵表达形式为
(3) $Y=X\beta$
这里将 $b$ 也统一到矩阵 $X$ 中去了，比如对于前面的一元线性回归 $y=\alpha+\beta{x}$ ,用该矩阵表示就是
$[y] = [1 x] [α β]$ $[\begin{matrix} y \end{matrix}]= [\begin{matrix} 1&x \end{matrix}] [\begin{matrix} \alpha\\ \beta \end{matrix}]$
对于式子(3)即需要解一个 $\beta$ 使得损失最小，根据线性代数和最优化理论的知识，可以解得
(4) $\beta=(X^TX)^{-1}X^TY$
时求得方程(1)得系数矩阵。

#验证上述式子，在上面的代码后面添加如下代码：
w, b = np.dot(np.linalg.inv(np.dot(np.transpose(X), X)), np.dot(np.transpose(X), Y))
#输出和上面一样的w和b
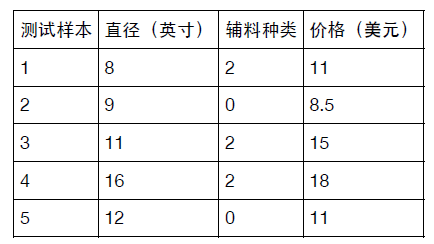
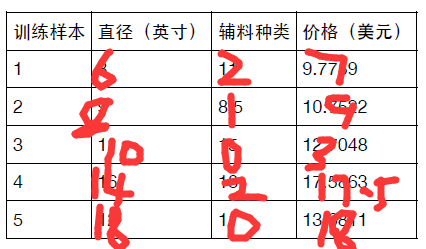
print(w, b)

下面对于多元回归模型进行测试，假设在前面的披萨模型中，价格除了和尺寸有关以外，还和所加辅料种
类有关，有如下训练数据和测试数据

这里写图片描述

在训练多元回归模型之前，我们先用R方来评估模型的性能，首先R方指标定义为：
(5) $R^2=1-\frac{\sum_{i=1}^{n}{(y_i-f(x_i))^2}}{\sum_{i=1}^{n}{(y_i-y*)}}$
其中 $f(x_i)$ 为模型对样本数据计算结果， $y*$ 为样本数据中 $y$ (上述例子中的价格)的均值。R方指标在model中可调用score函数求得。
下面我们对上面表格中的数据，在只考虑尺寸的情况下计算一下模型的性能：

#在上述代码后添加：
X = [[6], [8], [10], [14], [18]]
Y = [[7], [9], [13], [17.5], [18]]
model.fit(X, Y)
test_x = [[8], [9], [11], [16], [12]]
test_y = [[11], [8.5], [15], [18], [11]]
score = model.score(test_x, test_y)
#输出为0.66
print("只考虑尺寸时模型得分：", score)
plt.plot(model.predict(test_x), 'r-')

可以看到这种情况下算出来的R方为0.662，它大致可以表述为测试集中过半数的价格都可以通过模型解释，但是这个效果显然并不是最好。

下面我们加上辅料这一信息进行二元回归：

X = [[6, 2], [8, 1], [10, 0], [14, 2], [18, 0]]
Y = [[7], [9], [13], [17.5], [18]]
model.fit(X, Y)
test_x = [[8, 2], [9, 0], [11, 2], [16, 2], [12, 0]]
test_y = [[11], [8.5], [15], [18], [11]]
score = model.score(test_x, test_y)
#输出为0.77
print("同时考虑尺寸和辅料时模型得分：", score)
plt.plot(model.predict(test_x), 'g-')
plt.plot(test_y, 'b-')
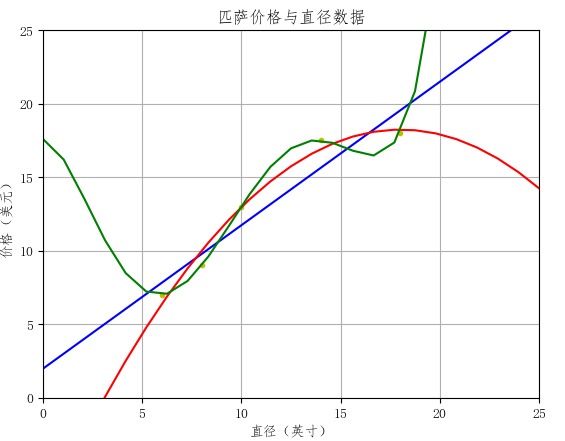
plt.show()

下图蓝色曲线是真实价格曲线，红色是一元回归的结果，绿色是二元回归结果：
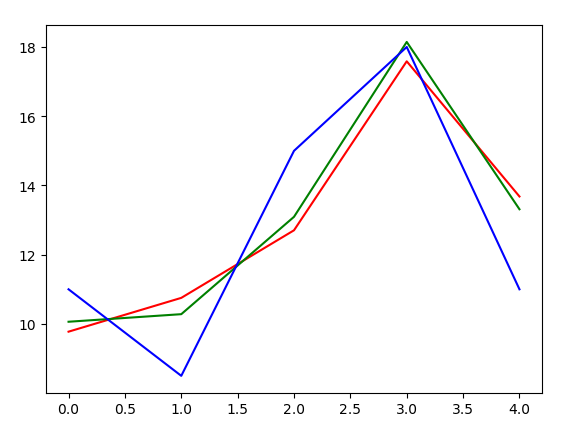
这里写图片描述
可以看到，虽然两种预测结果都不是和真实价格十分吻合，但是绿色曲线显然跟拟合蓝色曲线。拿预测结果来说，利用了两种信息的二元回归模型所预测出来的价格距离真实价格跟接近，R指标也更大，所以性能比只利用尺寸这一信息要好许多。

至于两种线性回归的结果都不是特别好，因此，下面介绍多项式回归，它可以更加拟合训练样本数据。

多项式回归
上面的例子中，我们只能对现有样本进行直线拟合，但是可能真实的数据并完全满足线性关系。下面我们使用多项式回归。
前面我们的一元线性回归模型可以用公式 (2)y=α+βx表示，看到，除了两个参数外，自变量的最高项的次数为1，而多项式回归的改进在于，增加自变量的次数，比如一元二次回归模型可以用公式
(6) y=α+β1x+β2x2
来拟合。这里参数从原来的两个变成了三个，我们可以通过实际例子来比较它和一元一次线性回归模型的性能差别。假设有下面数据：
```
#一元线性回归
X_train = [[6], [8], [10], [14], [18]]
Y_train = [[7], [9], [13], [17.5], [18]]
linear_model = LinearRegression()
linear_model.fit(X_train, Y_train)
X_test = np.linspace(0, 25, 25)
X_test = X_test.reshape(X_test.shape[0], 1)
Y_pre = linear_model.predict(X_test)
#输出0.91
print("一元线性回归的R方为：", linear_model.score(X_train, Y_train))
plt.plot(X_train, Y_train, 'y.')
plt.plot(X_test, Y_pre, 'b-')

#多项式回归
quadratic_featurizer = PolynomialFeatures(degree=2)
X_train_quadratic = quadratic_featurizer.fit_transform(X_train)
X_test_quadratic = quadratic_featurizer.fit_transform(X_test)
linear_model.fit(X_train_quadratic, Y_train)
Y_pre = linear_model.predict(X_test_quadratic)
#输出0.98
print("二次多项式回归的R方为：", linear_model.score(X_train_quadratic, Y_train))
plt.plot(X_test, Y_pre, 'r-')
plt.show()
```
可以看出，二次多项式回归的能够拟合曲线，即其学习能力更强，通过上面的例子，可以看到多项式回归的R方比一元线性回归的R方要大许多。

或许你认为如果我们把二次多项式换成更高次的多项式，岂不是拟合效果更好，那结果是不是会大幅度提高呢？我们将二次多项式改为10次多项式看看结果：
```
quadratic_featurizer = PolynomialFeatures(degree=5)
X_train_quadratic = quadratic_featurizer.fit_transform(X_train)
X_test_quadratic = quadratic_featurizer.fit_transform(X_test)
linear_model.fit(X_train_quadratic, Y_train)
Y_pre = linear_model.predict(X_test_quadratic)
#输出1
print("五次多项式回归的R方为：", linear_model.score(X_train_quadratic, Y_train))
plt.plot(X_test, Y_pre, 'g-')
plt.show()
```
看上面输出结果R方为1了，说明这条绿色曲线能够完全拟合训练数据，即训练数据在坐标系中对应的点都过这条绿色的曲线，然而我们可以看到，这条绿色的曲线其实并能很好的表示”尺寸越大，价格越高“这一事实，也就是说，如果我们预测的数据不是来自训练样本，那么，误差会很大。这就是过拟合现象。我们可以通过正则化来降低过拟合。
- 线性回归应用案例
我们使用UCI机器学习项目的酒数据集，一共有1599种酒的测试数据，其中属性取值是0到10之间的整数值。数据下载地址
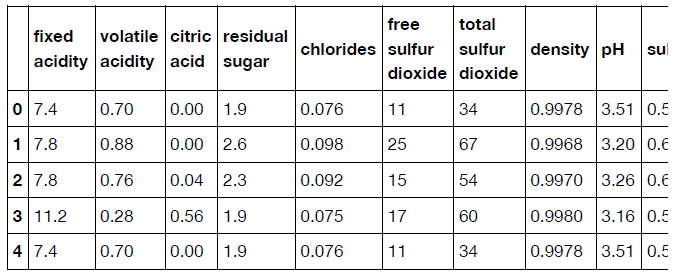
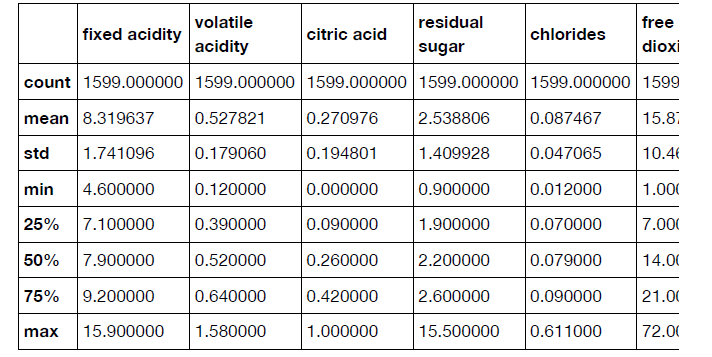
首先，我们读取.csv文件生成dataframe，可以查看数据的格式和一些统计信息：
```
import pandas as pd
df = pd.read_csv('winequality-red.csv', sep=';')
print(df.head())
print(df.describe())
```
分别输出下表信息：

下面通过matplotlib绘制数据：
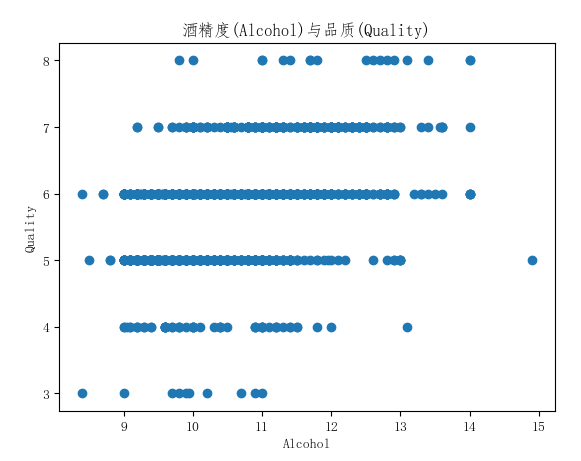
```
import matplotlib.pyplot as plt
plt.scatter(df['alcohol'], df['quality'])
plt.xlabel('Alcohol')
plt.ylabel('Quality')
plt.title('酒精度(Alcohol)与品质(Quality)')
plt.show()
```
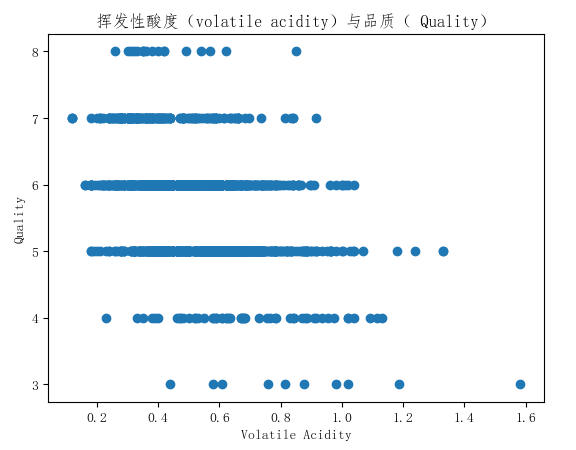
通过绘制散点图可以看到酒精度和其品质有相对比较弱的正相关的特性，也就是酒精度高的酒可能品质更高。再看看挥发性酸性和酒精品质的相关性：

可以看出挥发性酸和酒精的品质呈负相关。但是我们并不知道每个特性对酒的品质的影响到底有多大，因此，我们可以使用前面的回归模型进行建模。

先将数据分为训练集和测试集，训练回归模型然后评估预测效果：
```
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split


def set_ch():
    from pylab import mpl
    # 指定默认字体
    mpl.rcParams['font.sans-serif'] = ['FangSong']
    # 解决保存图像是负号'-'显示为方块的问题
    mpl.rcParams['axes.unicode_minus'] = False
set_ch()

df = pd.read_csv('winequality-red.csv', sep=';')
#取出除了label列的所有列的head和label标签
feature = df[list(df.columns)[:-1]]
label = df['quality']
x_train, x_test, y_train, y_test = train_test_split(feature, label)
model = LinearRegression()
model.fit(x_train, y_train)
#这里输出的值每次都不一样，因为上面使用了随机划分训练集和测试集
print("R方为：", model.score(x_test, y_test))
```
为了降低因为训练样本选取所带来的随机性，我们可以使用交叉验证来降低这种随机性：
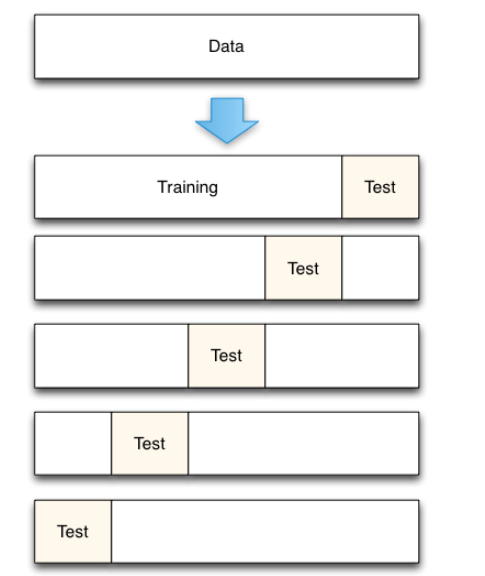
```
import sklearn
scores = sklearn.model_selection.cross_val_score(model, feature, label, cv=5)
print(scores.mean(), scores)
```
cross_val_score可以实现交叉验证功能，其原理如下图：
- 梯度下降法拟合模型
  前面讲的方法都是使用最小化损失函数来计算参数的，也就是公式(4) $\beta=(X^TX)^{-1}X^TY$ 。但是当样本的属性很大时， $X^TX$ 的计算量很大，而且如果 $X^TX$ 的行列式为0，即奇异矩阵时，就无法求得其逆矩阵。所以我们使用另一种方法来求解最小化损失函数的参数。
  首先，我们前面用的损失函数如下：
  (7) $SS_res=\sum_{i=1}^{n}(y_i-f(x_i))^2$
  前面参数 $\beta$ 的求取是通过求导为0解得驻点进行求参的。
梯度下降法的具体推导过程这里就不做详细介绍，主要说一下梯度下降有三种方法，主要是根据每一次迭代时所使用的训练样本的选取方式来进行划分的。第一种是批量梯度下降，每次迭代使用的是所有的训练样本，但是这样做对于数据量巨大的时候迭代会变得异常缓慢；另一种是随机梯度下降，也就是每一次随机从样本中选取一个样本进行训练，但是因为每一次只取一个，所含信息量是很少的，可能会导致收敛过程很震荡；另一种方法是随机批量梯度下降，这种方法综合了前两种方法的优缺点，一般比较常用。

下面使用sklearn的SGDRegressor类来计算模型参数。它可以通过优化不同的成本函数来拟合线性模型，默认的损失函数为上面(7)中的据方误差。

我们使用波士顿住房数据的13个解释变量来预测房屋价格：
首先加载数据集和分割训练集和测试集：
```
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_boston
from sklearn.linear_model import SGDRegressor
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
import numpy as np

def set_ch():
    from pylab import mpl
    # 指定默认字体
    mpl.rcParams['font.sans-serif'] = ['FangSong']
    # 解决保存图像是负号'-'显示为方块的问题
    mpl.rcParams['axes.unicode_minus'] = False
set_ch()

data = load_boston()
x_train, x_test, y_train, y_test = train_test_split(data.data, data.target)
```
然后我们对数据进行归一化处理：
```
y_train = np.reshape(y_train, (y_train.shape[0], 1))
y_test = np.reshape(y_test, (y_test.shape[0], 1))
x_scaler = StandardScaler()
y_scaler = StandardScaler()
x_train = x_scaler.fit_transform(x_train)
y_train = y_scaler.fit_transform(y_train)
x_test = x_scaler.transform(x_test)
y_test = y_scaler.transform(y_test)
```
这里使用StandarScaler进行归一化处理，后面会介绍。最后我们使用交叉验证来完成训练和测试：
```
model = SGDRegressor(loss='squared_loss')
scores = cross_val_score(model, x_train, y_train, cv=5)
print('交叉验证的R方值和均值：', scores, scores.mean())
model.fit(x_train, y_train)
print('测试集R方值：', model.score(x_test, y_test))
```
下一篇文章，将介绍处理不同类型的数据的方法，包括分类数据，文字，图像等。

主要参考资料：
Mastering Machine Learning With scikit-learn（中文文字版）
机器学习-周志华清华大学出版社

注：转载请注明原文出处：
作者：CUG_UESTC
出处：http://blog.csdn.net/qq_31192383/article/details/78723468

机器学习与scikit-learn（一）——回归模型

安装

线性回归

悦读