【数据结构与算法——TypeScript】数组、栈、队列、链表

【数据结构与算法——TypeScript】

算法(Algorithm)的认识

解决问题的过程中，不仅仅 数据的存储方式会影响效率，算法的优劣也会影响效率
什么是算法？
- 定义：
  🟢 一个有限指令集，每条指令的描述不依赖于言语（编写指令：java/c++/ts/js）
  🟢 接收一些输入（有些情况下不需要输入）（接收：排序：无序数组）
  🟢 产生输出（产出：有序数组）
  🟢 一定在有限步骤之后终止
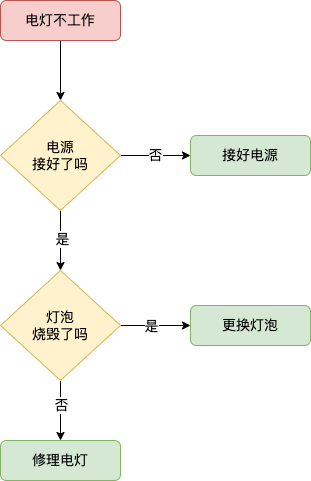
举例：电灯不工作的解决算法
算法的通俗理解
- Algorithm这个单词本意就是 解决问题的办法/步骤逻辑。
- 数据结构的实现，离不开算法。

线性结构(Linear List)

线性结构（Linear List）是由n（n≧0）个数据元素（结点）a[0],a[1],a[2],…,a[n-1]组成的有限序列。
其中：
- 【数据元素的个数 n 定义为表的长度】= “list”.length()(“list”.length() = 0 (表示没有一个元素) 时，称为空表)。
- 将非空的线性表（n>=1）,记作：（a[0],a[1],a[2],…,a[n-1]）。
- 数据元素 a[i] (0 <= i <= n-1) 只是抽象符号，其具体含义在不同情况下可以不同。
常见线性结构：
💚 数组结构（Array）
💚 栈结构（Stack）
💚 队列结构（Queue）
💚 链表结构（LinkedList）

数组(Array)结构

数组(Array)结构是一种重要的数据结构
- 几乎是每种编程语言都会提供的一种 原生数据结构（语言自带的）；
- 并且我们 可以借助于数组结构来实现其他的数据结构，比如：栈（Stack）、队列（Queue）、堆（Heap）；
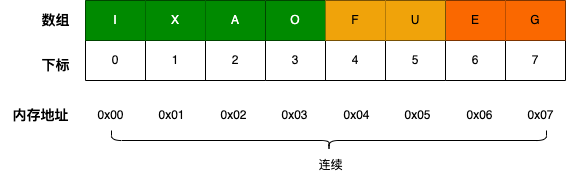
通常数组的内存都是连续的，所以数组在知道下标值的情况下，访问效率是非常高的
TypeScript中数组的各种用法，和JavaScript是一致的：
https://developer.mozilla.org/zh-CN/docs/Web/JavaScript/Reference/Global_Objects/Array

栈结构(Stack)

认识栈结构和特性 ❤️

认识栈结构

栈也是一种非常常见的数据结构，并且在程序中的应用非常广泛。
数组：
- 是一种 线性结构，可以在数组的 任意位置 插入和删除数据。
- 但，为了实现某些功能，必须对这种 任意性加入限制。
- 而 栈和队列 就是比较常见的 受限的线性结构。
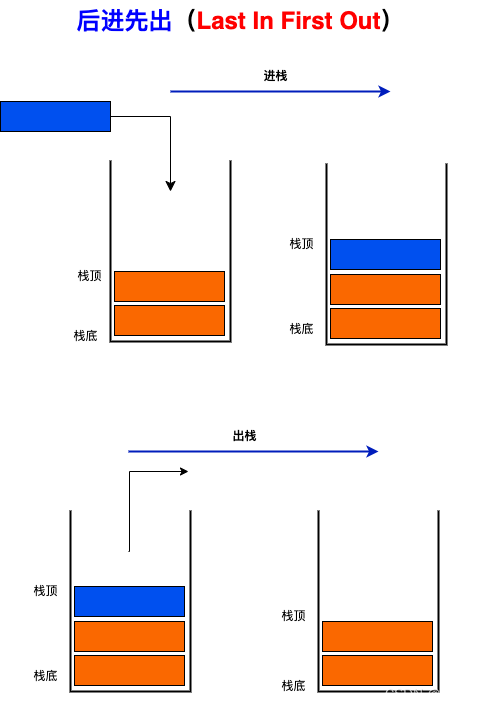
栈结构示意图
❤️ 后进先出/先进后出

栈结构特性

栈（Stack）,它是一种受限的线性结构， 后进先出（LIFO）
- 其限制是仅允许在 表的一端 进行插入和删除运算。这一端被称为栈顶，相对地，另一端就是栈低。
- LIFO（last in first out）表示后进入的元素，第一个弹出栈空间。类似于，自动餐托盘，最后放上的托盘，往往先拿出去使用。
- 向一个栈插入新元素，又叫 进栈、入栈或压栈，它是把新元素放到栈顶元素的上面，使之成为新的栈顶元素；
- 从一个栈删除元素又称之为 出栈或者退栈，它是把栈顶元素删除掉，使其相邻的元素成为新的栈顶元素。

栈结构特性 —— 面试题

面试题目

❓题目：
🔖 有六个元素6,5,4,3,2,1顺序入栈,问下列哪一个不是合法的出栈序列?()
A. 5 4 3 6 1 2
B. 4 5 3 2 1 6
C. 3 4 6 5 2 1
D. 2 3 4 1 5 6
分析：
- A. 5 4 3 6 2 1
  - 6，5进栈，5出栈，4进栈，4出栈，3进栈，3出栈，6出栈，2进栈，1进栈，1出栈，2出栈
- B. 4 5 3 2 1 6
  - 6，5，4进栈，4出栈，5出栈，3进栈，3出栈，2进栈，2出栈，1入栈，1出栈，6出栈
- C. 3 4 6（x） 5 2 1 ❌
  - 6，5，4，3进栈，3出栈，4出栈，5出栈
- D. 2 3 4 1 5 6
  - 6，5，4，3，2进栈，2出栈，3出栈，4出栈，1进栈，1出栈，5出栈，6出栈
- 答案： C

实现栈结构的封装

常见的方式：
🔹 基于数组实现
🔹 基于链表实现

🔹 基于数组实现：创建栈的类

代码解析：
- 创建一个 Stack ，用户创建栈的类，可以定义一个泛型类。
- 在构造函数中，定义一个变量，存储当前栈对象中的所有元素。
- 这个变量是一个数组类型。
- 之后，无论是入栈还是出栈操作，都是从数组中添加和删除元素。
- 栈的一些操作方法，无论是什么语言，操作都是比较类似的。

栈结构常见的方法

🔸栈的常见操作

push(element):添加一个新元素到栈顶。
pop()：删除栈顶元素，返回被移除的元素。
peek():仅返回栈顶元素，不对栈做任何修改。
isEmpty():判断栈里是否有元素。有，返回true，否，返回false。
size():返回栈里的元素个数。这个方法和数组的length属性类型。

实现

import { IStack } from './IStack';

class ArrayStack<T = any> implements IStack<T> {
  // 定义一个数组/链表，用于存储元素
  private data: T[] = [];
  // 实现栈中的操作方法
  // push(element)：添加一个新元素到栈顶
  push(element: T): void {
    this.data.push(element);
  }
  // pop()：删除栈顶元素，返回被移除的元素。
  pop(): T | undefined {
    return this.data.pop();
  }
  // peek():仅返回栈顶元素，不对栈做任何修改。
  peek(): T | undefined {
    return this.data[this.data.length - 1];
  }
  // isEmpty():判断栈里是否有元素。有，返回true，否，返回false。
  isEmpty(): boolean {
    return this.data.length === 0;
  }
  // size():返回栈里的元素个数。这个方法和数组的length属性类型。
  size(): number {
    return this.data.length;
  }
}

export default ArrayStack;

export interface IStack<T> {
  push(element: T): void;
  pop(): T | undefined;
  peek(): T | undefined;
  isEmpty(): boolean;
  size(): number;
}

栈面试题 —— 十进制转二进制

为什么需要十进制转二进制？
- 现实生活中，主要使用 十进制。
- 但，在计算机科学中， 二进制非常重要，因为 计算机里的所有内容都是用二进制数字表示的（0和1）。
- 没有十进制和二进制互相转换的能力，与计算机交流就很困难。
- 转换二进制是计算机科学和编程领域中经常使用的算法。
如何实现时十进制转二进制(整数)？
- 将十进制数字和2整除（二进制是满2进1），直到结果为0
- 把十进制数字35转为二进制的数字：
  - 35/2 = 17…1, 余 1
  - 17/2 = 8…1, 余 1
  - 8/2 = 4…0,余 0
  - 4/2 = 2…0,余 0
  - 2/2 = 1…0,余 0
  - 1/2 = 0…1,余 1
  - 从后往前：100011

简单实现

import ArrayStack from './02_实现栈结构Stack(重构)';

function decimalToBinary(decimal: number): string {
  // 1. 创建一个栈，用于存储余数
  const stack = new ArrayStack<number>();
  // 2. 使用循环:while:不确定次数，只知道循环结束条件
  while (decimal > 0) {
    const result = decimal % 2;
    stack.push(result);
    decimal = Math.floor(decimal / 2);
  }
  // 3.将所有的余数已放入到stack中，依次取出所有余数
  let binary = '';
  while (!stack.isEmpty()) {
    binary += stack.pop();
  }
  return binary;
}
export {};

console.log('35:', decimalToBinary(35));
console.log('100:', decimalToBinary(100));

栈面试题 —— 有效括号

给定一个只包括 ‘(’，‘)’，‘{’，‘}’，‘[’，‘]’ 的字符串 s ，判断字符串是否有效。
- ❗️有效字符串需满足：
  - 左括号必须用相同类型的右括号闭合。
  - 左括号必须以正确的顺序闭合。
  - 每个右括号都有一个对应的相同类型的左括号
  - Leecode 20:https://leetcode.cn/problems/valid-parentheses/
示例 1：

输入：s = “()”
输出：true
示例 2：

输入：s = “()[]{}”
输出：true
示例 3：

输入：s = “(]”
输出：false
⚠️ 提示：
- 1 <= s.length <= 10的4次
- s 仅由括号 ‘()[]{}’ 组成
代码

import ArrayStack from './02_实现栈结构Stack(重构)';

function isValid(s: string): boolean {
  // 1. 创建一个栈结构：
  const stack = new ArrayStack<string>();
  // 2. 遍历字符串
  for (let i = 0; i < s.length; i++) {
    const c = s[i];
    switch (c) {
      case '(':
        stack.push(')');
        break;
      case '{':
        stack.push('}');
        break;
      case '[':
        stack.push(']');
        break;
      default:
        if (c !== stack.pop()) return false;
        break;
    }
  }
  return stack.isEmpty();
}

console.log(isValid('()'));
console.log(isValid('()[]{}'));
console.log(isValid('(]'));
console.log(isValid('([])'));
console.log(isValid('({[}])'));

队列结构(Queue)

认识队列和特性

受限的线性结构
- 这种受限的线性结构对于解决某些 特别问题有特别的结果。
- 受限的数据结构：队列。
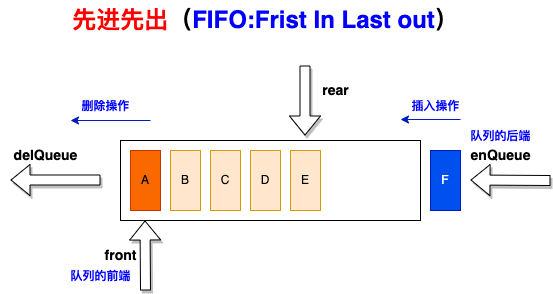
队列（Queue），它是一种受限的线性结构，先进先出（FILO:First In Last Out）
- 受限之处：只允许在队列的前端（front），进行删除操作；
- 在队列的 后端（rear) 进行插入操作；

实现队列结构封装

基于数组实现（性能低）
基于链表实现（更好）

队列结构常见方法

enqueue(element):向队列尾部添加一个（或者多个）新的项。
dequeue():移除队列的第一（即排在队列最前面的）项，也是最先移除的元素；
front/peek():返回队列中第一个元素——最先被添加，也是最先被移除的元素。队列不做任何变动（不移除元素，只返回元素信息）
isEmpty():如果队列中不包含任何元素，返回true，否则返回false
size():返回队列包含的元素个数，与数组的length属性类似

基于数组实现

import { IQueue } from './IQueue';

class ArrayQueue<T = any> implements IQueue<T> {
  // 内部通过数组保存
  private data: T[] = [];
  // 队列常见操作
  /**
   * enqueue(element):向队列尾部添加一个（或者多个）新的项。
   * dequeue():移除队列的第一（即排在队列最前面的）项，也是最先移除的元素；
   * front/peek():返回队列中第一个元素——最先被添加，也是最先被移除的元素。队列不做任何变动（不移除元素，只返回元素信息）
   * isEmpty():如果队列中不包含任何元素，返回true，否则返回false；
   * size():返回队列包含的元素个数，与数组的length属性类似
   */
  enqueue(element: T): void {
    this.data.push(element);
  }
  dequeue(): T | undefined {
    return this.data.shift();
  }
  peek(): T | undefined {
    return this.data[0];
  }
  isEmpty(): boolean {
    return this.data.length === 0;
  }
  get size(): number {
    return this.data.length;
  }
}
export default ArrayQueue;

import type { IList } from '../types/IList';

export interface IQueue<T> extends IList<T> {
  enqueue(element: T): void;
  dequeue(): T | undefined;
}

export interface IList<T> {
  peek(): T | undefined;
  isEmpty(): boolean;
  get size(): number;
}

面试题 —— 击鼓传花

击鼓传花，是一个常见的面试算法题：使用队列可以非常方便的实现最终的结果
原游戏规则
- 班级中玩一个游戏，所有同学围成一个圈，从某位同学手里开始向旁边的同学传一束花；
- 这个时候某个人（比如班长），在击鼓，鼓声停下的一刻，花落在谁的手里，谁就出来表演节目。
修改游戏规则
- 几个朋友一起玩一个游戏， 围成一圈，开始数数，数到某个数字的人自动淘汰；
- 最后 剩下的这个人获胜，请问最后剩下的人是原来在哪一个位置上的人？
封装一个基于队列的函数：
- 参数：所有参与人的姓名，基于的数字；
- 结果：最终剩下的一个人的姓名
分析：
- 假如数到3的人，淘汰；
  - 那么，队列中数的1，2的人，出队之后，又入队；
  - 数到 3 的人，出队，不需要入队
- 直到，队列的size() 等于1 的时候，取到队列里的人
代码

import ArrayQueue from './01_基于数组的队列结构Queue';

function hotPatato(names: string[], num: number) {
  if (names.length === 0) return -1;
  // 1. 创建一个队列结构
  const queue = new ArrayQueue<string>();
  // 2. 将所有的name加入队列
  for (const name of names) {
    queue.enqueue(name);
  }
  // 3. 淘汰的规则
  while (queue.size > 1) {
    // 小于 num 的不淘汰
    for (let i = 1; i < num; i++) {
      const name = queue.dequeue();
      if (name) queue.enqueue(name);
    }
    // num 淘汰
    queue.dequeue();
  }
  // 取出最后一个人
  const leftName = queue.dequeue()!;
  // 取出最后一个人的原索引
  const index = names.indexOf(leftName);
  return index;
}
const leftIndex = hotPatato(['why', 'JIM', 'JANE', 'LENO', 'CURRY', 'TIM', 'TOM', 'JERRY', 'JENO', 'TIA'], 5);
console.log(leftIndex);

面试题 —— 约瑟夫环

什么是约瑟夫环问题（历史）？
阿乔问题（有时也称为约瑟夫斯置换），是一个出现在计算机科学和数学中的问题。在计算机编程的算法中，类似问题又称为约瑟夫环。
- 人们站在一个等待被处决的圈子里；
- 计数从圆圈中指定的点开始，并沿指定方向围绕圆圈进行；
- 在跳过指定数量的人之后，处刑下一个人；
- 对剩下的人重复该过程，从下一个人开始，朝同一方向跳过相同数量的人，直到只剩下一个人，并被释放；
- 在给定数量的情况下，站在第几个位置可以避免被处刑？
Leecode 剑指 Offer 62. 圆圈中最后剩下的数字
https://leetcode.cn/problems/yuan-quan-zhong-zui-hou-sheng-xia-de-shu-zi-lcof/
0,1,···,n-1这n个数字排成一个圆圈，从数字0开始，每次从这个圆圈里删除第m个数字（删除后从下一个数字开始计数）。
求出这个圆圈里剩下的最后一个数字。
例如，0、1、2、3、4这5个数字组成一个圆圈，从数字0开始每次删除第3个数字，则删除的前4个数字依次是2、0、4、1，因此最后剩下的数字是3。
示例 1：

输入: n = 5, m = 3
输出: 3
示例 2：

输入: n = 10, m = 17
输出: 2
代码

import ArrayQueue from './01_基于数组的队列结构Queue';

function lastRemaining(n: number, m: number): number {
  const queue = new ArrayQueue<number>();
  for (let i = 0; i < n; i++) {
    queue.enqueue(i);
  }
  while (queue.size > 1) {
    for (let i = 1; i < m; i++) {
      queue.enqueue(queue.dequeue()!);
    }
    queue.dequeue();
  }
  return queue.dequeue()!;
}

console.log(lastRemaining(5, 3));
console.log(lastRemaining(10, 17));

链表结构（LinkedList）

认识链表及特性

数组的缺点

链表和数组一样，可以用于 存储一系列的元素，但是链表和数组的 实现机制完全不同。
用于存储数据的线性结构：链表。

🥺

数组：
- 要存储多个元素，数组（或选择链表）可能是 最常用的数据结构
- 几乎每种语言都有默认实现 数组结构
💔 但是，数组有很多缺点
- 数组的创建通常需要申请一段 连续的内存空间（一整块的内存），并且大小是固定的（大多数编程语言数组都是固定的），所以当前数组 不能满足容量需求时，需要扩容。（一般情况下时申请一个更大的数组，比如2倍。然后将原数组中的元素复制过去）
- 而且在 数组开头或者中间位置插入数据的成本很高，需要 进行大量元素的位移。

🥰 链表的优势

要存储多个元素，另外一个选择就是链表
不同于数组，链表中的元素在内存中 不必是连续的空间。
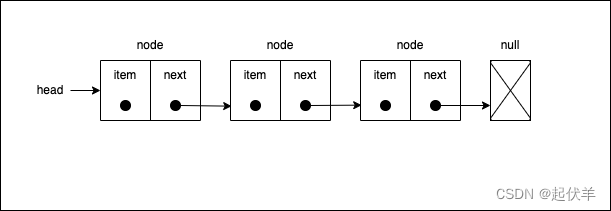
- 链表的每个元素由一个存储 元素本身的节点和 一个指向下一个元素的引用（有些语音称为指针或链接）组成。
❣️ 相对于数组，链表的优势有
- 🟩 内存空间不是必须连续的
  - ✓ 可以充分利用计算机的内存，实现灵活的 内存动态管理。
- 🟩 链表不必在创建时就 确定大小，并且大小可以 无限延伸下去。
- 🟩 链表在 插入和删除数据时，时间复杂度可以达到O(1)
  - ✔️ 相对数组效率高很多
💔 相对于数组，链表的缺点有
- ❌ 链表访问任何一个位置的元素时，都需要 从头开始访问（无法跳过第一个元素访问任何一个元素）。
- ❌ 无法通过下标直接访问元素，需要从头一个一个访问，直到找到对应的元素。

什么是链表？

链表是什么？
- 链表类似于火车：有一个火车头，火车头会连接一个节点，节点上有乘客（类似于数据），并且这个节点会连接下一个节点，以此类推。

在这里插入图片描述

封装链表的类结构

分析代码

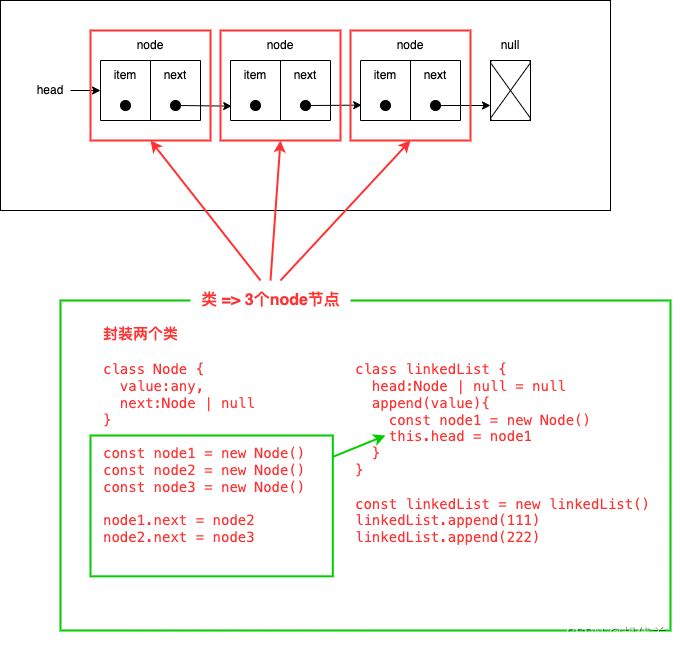
在这里插入图片描述

封装一个 Node类，用于封装每一个节点上的信息（包括值和指向下一个节点的引用），它是一个泛型。
封装一个 LinkedList类，用于表示我们的链表结构。
链表中保存两个属性：链表长度、链表的第一个节点。

// 1. 创建Node节点类
class Node<T> {
  value: T;
  next: Node<T> | null = null;
  constructor(value: T) {
    this.value = value;
  }
}

// 2.创建LinkedList类
class LinkedList<T> {
  head: Node<T> | null = null;
  private size: number = 0;

  get length() {
    return this.size;
  }
}

const linkedList = new LinkedList<string>();
console.log(linkedList.head);
export {};

封装链表的相关方法

append(element):向链尾添加一个新的项
- 1. 链表本身为空，新添加数据时唯一的节点
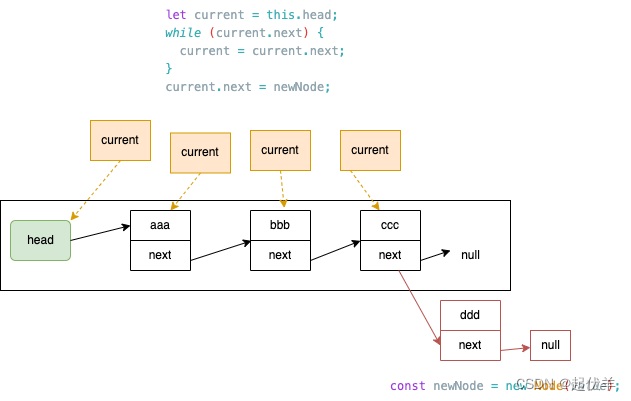
- 1. 链表本身不为空，需要向其他节点后面追加节点

  // 追加节点
  append(value: T) {
    // 1.根据value创建一个新节点
    const newNode = new Node(value);
    //  1. 链表本身为空，新添加数据时唯一的节点
    //  2. 链表本身不为空，需要向其他节点后面追加节点
    if (!this.head) {
      this.head = newNode;
    } else {
      let current = this.head;
      while (current.next) {
        current = current.next;
      }
      // current此时，肯定是指向最后一个节点
      current.next = newNode;
    }
    this.size++;
  }

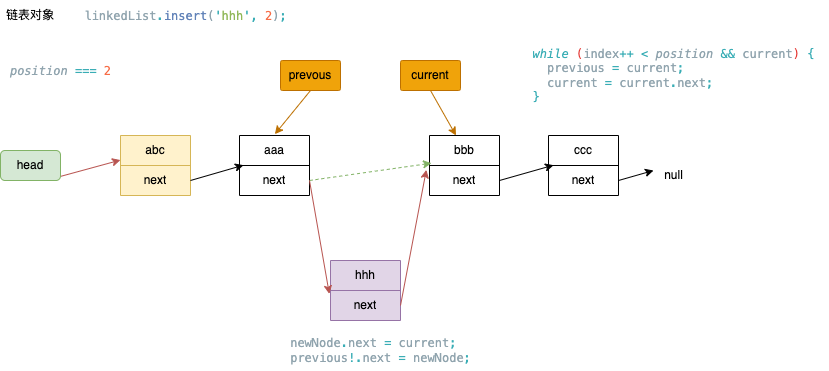
insert(position,element):向链表的特定位置插入一个新的项
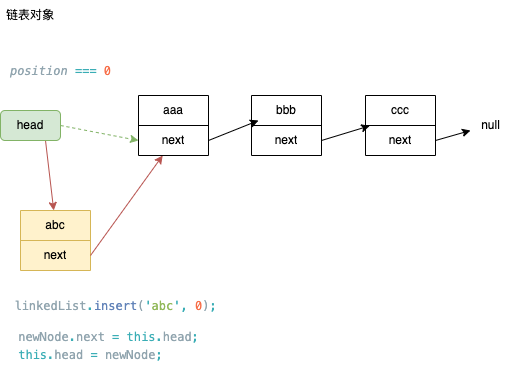
- 1.添加到第一个位置
  - 添加到第一个位置，表示新添加的节点是头，就需要将原来的头节点，作为新的节点的next
  - 这个时候的head应该指向新节点
- 1. 其他位置

- 在这里插入图片描述

  //插入 insert(position, element): 向链表的特定位置插入一个新的项;
  insert(value: T, position: number): boolean {
    if (position < 0 || position > this.size) return false;
    // 是否添加到第一个
    const newNode = new Node(value);
    if (position === 0) {
      newNode.next = this.head;
      this.head = newNode;
    } else {
      let current = this.head;
      let previous: Node<T> | null = null;

      let index = 0;
      while (index++ < position && current) {
        previous = current;
        current = current.next;
      }
      // index === position
      newNode.next = current;
      previous!.next = newNode;
    }
    this.size++;
    return true;
  }

get(position):获取对应位置的元素

  // 获取get
  get(position: number): T | null {
    if (position < 0 || position >= this.size) return null;
    // 查找元素
    let index = 0;
    let current = this.head;
    while (index++ < position && current) {
      current = current?.next;
    }
    // index === position
    return current?.value ?? null;
  }

indexOf(element):返回元素在链表中的索引。如果链表中没有该元素则返回 -1

  // 获取索引
  indexOf(value: T): number {
    // 遍历
    let current = this.head;
    let index = 0;
    while (current) {
      if (current.value === value) {
        return index;
      }
      current = current.next;
      index++;
    }
    return -1;
  }

update(position,element):修改某个位置的元素

  // 更新
  update(value: T, position: number): boolean {
    if (position < 0 || position >= this.size) return false;

    let currentNode = this.head;
    let index = 0;
    while (index++ < position && current) {
      currentNode = currentNode.next;
    }
    
    currentNode!.value = value;
    return true;
  }

removeAt(position):从链表的特定位置移除一项
- 常见两种
  - 1. 根据位置位移对应的数据
  - 1. 根据数据，先找到对应的位置，再移除数据
- 移除第一项：
  - 移除第一项时，直接让head指向第二项信息
  - 第一项信息没有引用指向，就在链表中不再有效，后面会被回收
- 移除其他项：
  - 首先，通过while循环，找到正确的位置
  - 其次，直接将上一项的next指向current项的next，这样中间的项就没有引用指向它，也就不存于链表中，后面就会被回收

  // 删除
  removeAt(position: number): T | null {
    // 越界判断
    if (position < 0 || position >= this.size) return null;
    // 删除元素
    // 判断是否是删除第一个节点
    let current = this.head;
    if (position === 0) {
      this.head = this.head?.next ?? null;
    } else {
      let previous: Node<T> | null = null;
      let index = 0;
      while (index++ < position && current) {
        previous = current;
        current = current.next;
      }
      // index === position
      previous!.next = current?.next ?? null;
    }
    this.size--;
    return current?.value ?? null;
  }

remove(element):从链表中移除一项

  // 根据value删除
  remove(value: T): T | null {
    const index = this.indexOf(value);
    return this.removeAt(index);
  }

isEmpty():如果链表中不包含任何元素，返回true，如果链表长度大于0则返回false

// 链表是否为空
  isEmpty(): boolean {
    return this.size === 0;
  }

size():返回链表包含的元素个数。与数组的length属性类似

完整代码

// 1. 创建Node节点类
class Node<T> {
  value: T;
  next: Node<T> | null = null;
  constructor(value: T) {
    this.value = value;
  }
}

// 2.创建LinkedList类
class LinkedList<T> {
  private head: Node<T> | null = null;
  private size: number = 0;

  get length() {
    return this.size;
  }
  // 封装私有方法：
  // 根据position 获取到当前节点（不是节点的value，而是获取节点）
  private getNode(position: number): Node<T> | null {
    let current = this.head;
    let index = 0;
    while (index++ < position && current) {
      current = current.next;
    }
    return current;
  }
  // 追加节点
  append(value: T) {
    // 1.根据value创建一个新节点
    const newNode = new Node(value);
    //  1. 链表本身为空，新添加数据时唯一的节点
    //  2. 链表本身不为空，需要向其他节点后面追加节点
    if (!this.head) {
      this.head = newNode;
    } else {
      let current = this.head;
      while (current.next) {
        current = current.next;
      }
      // current此时，肯定是指向最后一个节点
      current.next = newNode;
    }
    this.size++;
  }
  // 遍历链表的方法
  traverse() {
    const values: T[] = [];
    let current = this.head;
    while (current) {
      values.push(current.value);
      current = current.next;
    }
    console.log(values.join(' -> '));
  }
  // 插入 insert(position, element): 向链表的特定位置插入一个新的项;
  insert(value: T, position: number): boolean {
    if (position < 0 || position > this.size) return false;
    // 是否添加到第一个
    const newNode = new Node(value);
    if (position === 0) {
      newNode.next = this.head;
      this.head = newNode;
    } else {
      let previous = this.getNode(position - 1);
      // index === position
      newNode.next = previous?.next ?? null;
      previous!.next = newNode;
    }
    this.size++;
    return true;
  }
  // 根据位置删除
  removeAt(position: number): T | null {
    // 越界判断
    if (position < 0 || position >= this.size) return null;
    // 删除元素
    // 判断是否是删除第一个节点
    let current = this.head;
    if (position === 0) {
      this.head = this.head?.next ?? null;
    } else {
      // 重构
      let previous = this.getNode(position - 1);
      // index === position
      previous!.next = previous?.next?.next ?? null;
    }
    this.size--;
    return current?.value ?? null;
  }
  // 获取get
  get(position: number): T | null {
    if (position < 0 || position >= this.size) return null;
    // 查找元素

    return this.getNode(position)?.value ?? null;
  }
  // 更新
  update(value: T, position: number): boolean {
    if (position < 0 || position >= this.size) return false;
    const currentNode = this.getNode(position);
    currentNode!.value = value;
    return true;
  }
  // 获取索引
  indexOf(value: T): number {
    // 遍历
    let current = this.head;
    let index = 0;
    while (current) {
      if (current.value === value) {
        return index;
      }
      current = current.next;
      index++;
    }
    return -1;
  }
  // 根据value删除
  remove(value: T): T | null {
    const index = this.indexOf(value);
    return this.removeAt(index);
  }
  // 链表是否为空
  isEmpty(): boolean {
    return this.size === 0;
  }
}
const linkedList = new LinkedList<string>();
linkedList.append('aaa');
linkedList.append('bbb');
linkedList.append('ccc');

linkedList.insert('abc', 0);
linkedList.insert('abcd', 0);

linkedList.insert('中间444', 2);
linkedList.insert('nba', 6);
linkedList.traverse();

linkedList.removeAt(0);
linkedList.traverse();
linkedList.removeAt(2);
linkedList.traverse();

console.log('-----测试get-----');
console.log(linkedList.get(0));
console.log(linkedList.get(1));
console.log(linkedList.get(2));

console.log('-----测试update-----');
console.log(linkedList.update('11111', 1));
linkedList.traverse();

console.log('-----测试indexOf-----');
console.log(linkedList.indexOf('11111'));
linkedList.traverse();
export {};

链表常见的面试题

1. 设计链表 https://leetcode.cn/problems/design-linked-list/
- 你可以选择使用单链表或者双链表，设计并实现自己的链表。
- 单链表中的节点应该具备两个属性：val 和 next 。val 是当前节点的值，next 是指向下一个节点的指针/引用。
- 如果是双向链表，则还需要属性 prev 以指示链表中的上一个节点。假设链表中的所有节点下标从 0 开始。
- 实现 MyLinkedList 类：
  - MyLinkedList() 初始化 MyLinkedList 对象。
  - int get(int index) 获取链表中下标为 index 的节点的值。如果下标无效，则返回 -1 。
  - void addAtHead(int val) 将一个值为 val 的节点插入到链表中第一个元素之前。在插入完成后，新节点会成为链表的第一个节点。
  - void addAtTail(int val) 将一个值为 val 的节点追加到链表中作为链表的最后一个元素。
  - void addAtIndex(int index, int val) 将一个值为 val 的节点插入到链表中下标为 index 的节点之前。如果 index 等于链表的长度，那么该节点会被追加到链表的末尾。如果 index 比长度更大，该节点将不会插入到链表中。
  - void deleteAtIndex(int index) 如果下标有效，则删除链表中下标为 index 的节点。

class Node<T> {
  val: T;
  next: Node<T> | null = null;
  constructor(val: T) {
    this.val = val;
  }
}
class MyLinkedList<T> {
  private head: Node<T> | null = null;
  private size: number = 0;
  private getNode(index: number): Node<T> | null {
    let current = this.head;
    let i = 0;
    while (i++ < index && current) {
      current = current.next;
    }
    return current;
  }
  // int get(int index) 获取链表中下标为 index 的节点的值。如果下标无效，则返回 -1 。
  get(index: number): any {
    if (index < 0 || index >= this.size) {
      return -1;
    }
    return this.getNode(index)?.val ?? null;
  }

  addAtHead(val: T): void {
    const newNode = new Node(val);
    newNode.next = this.head;
    this.head = newNode;
    this.size++;
  }

  addAtTail(val: T): void {
    const newNode = new Node(val);
    if (!this.head) {
      this.head = newNode;
    } else {
      let current = this.head;
      while (current.next) {
        current = current.next;
      }
      // current此时，肯定是指向最后一个节点
      current.next = newNode;
    }
    this.size++;
  }

  addAtIndex(index: number, val: T): boolean {
    if (index < 0 || index > this.size) return false;
    const newNode = new Node(val);
    if (index === 0) {
      newNode.next = this.head;
      this.head = newNode;
    } else {
      let previous = this.getNode(index - 1);
      // index === position
      newNode.next = previous?.next ?? null;
      previous!.next = newNode;
    }
    this.size++;
    return true;
  }

  deleteAtIndex(index: number): T | null {
    if (index < 0 || index >= this.size) return null;
    // 删除元素
    // 判断是否是删除第一个节点
    let current = this.head;
    if (index === 0) {
      this.head = this.head?.next ?? null;
    } else {
      // 重构
      let previous = this.getNode(index - 1);
      // index === position
      previous!.next = previous?.next?.next ?? null;
    }
    this.size--;
    return current?.val ?? null;
  }
}
export {};

1. 删除链表中的节点
- https://leetcode.cn/problems/delete-node-in-a-linked-list/
  有一个单链表的 head，我们想删除它其中的一个节点 node。
给你一个需要删除的节点 node 。你将无法访问第一个节点 head。

链表的所有值都是唯一的，并且保证给定的节点 node 不是链表中的最后一个节点。

删除给定的节点。注意，删除节点并不是指从内存中删除它。这里的意思是：
- 给定节点的值不应该存在于链表中。
- 链表中的节点数应该减少 1。
- node 前面的所有值顺序相同。
- node 后面的所有值顺序相同。
自定义测试：
- 对于输入，你应该提供整个链表 head 和要给出的节点 node。node 不应该是链表的最后一个节点，而应该是链表中的一个实际节点。
- 我们将构建链表，并将节点传递给你的函数。
- 输出将是调用你函数后的整个链表。

class ListNode {
  val: number;
  next: ListNode | null;
  constructor(val?: number, next?: ListNode | null) {
    this.val = val === undefined ? 0 : val;
    this.next = next === undefined ? null : next;
  }
}
function deleteNode(node: ListNode | null): void {
  node!.val = node!.next!.val;
  node!.next = node!.next!.next;
}
export {};

1. 反转链表
- https://leetcode.cn/problems/reverse-linked-list/
- 给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

class ListNode {
  val: number;
  next: ListNode | null;
  constructor(val?: number, next?: ListNode | null) {
    this.val = val === undefined ? 0 : val;
    this.next = next === undefined ? null : next;
  }
}

function reverseList(head: ListNode | null): ListNode | null {
  if (!head || !head.next) return head;

  const newHead = reverseList(head.next);

  head.next.next = head;
  head.next = null;
  return newHead;
}

【数据结构与算法——TypeScript】数组、栈、队列、链表

【数据结构与算法——TypeScript】

算法(Algorithm)的认识

线性结构(Linear List)

数组(Array)结构

栈结构(Stack)

认识栈结构和特性 ❤️

认识栈结构

栈结构特性

栈结构特性 —— 面试题

面试题目

实现栈结构的封装

🔹 基于数组实现：创建栈的类

栈结构常见的方法

实现

栈面试题 —— 十进制转二进制

栈面试题 —— 有效括号

队列结构(Queue)

认识队列和特性

实现队列结构封装

队列结构常见方法

基于数组实现

面试题 —— 击鼓传花

面试题 —— 约瑟夫环

链表结构（LinkedList）

认识链表及特性

数组的缺点

🥰 链表的优势

什么是链表？

封装链表的类结构

分析代码

封装链表的相关方法

完整代码

链表常见的面试题

悦读