2021SC@SDUSC
细分曲面是建模技术中面表示的重要方式，它通过存储低分辨率控制网格以及相关细分规则来获取平滑网格曲面，解决了任意拓扑和一致性表示问题，保留局部性、仿射不变性。例如，硬多边形建模的基本流程就是使用最少的面来表达物体的形状，再通过添加细分曲面使模型变得平滑。

Catmull-Clark细分

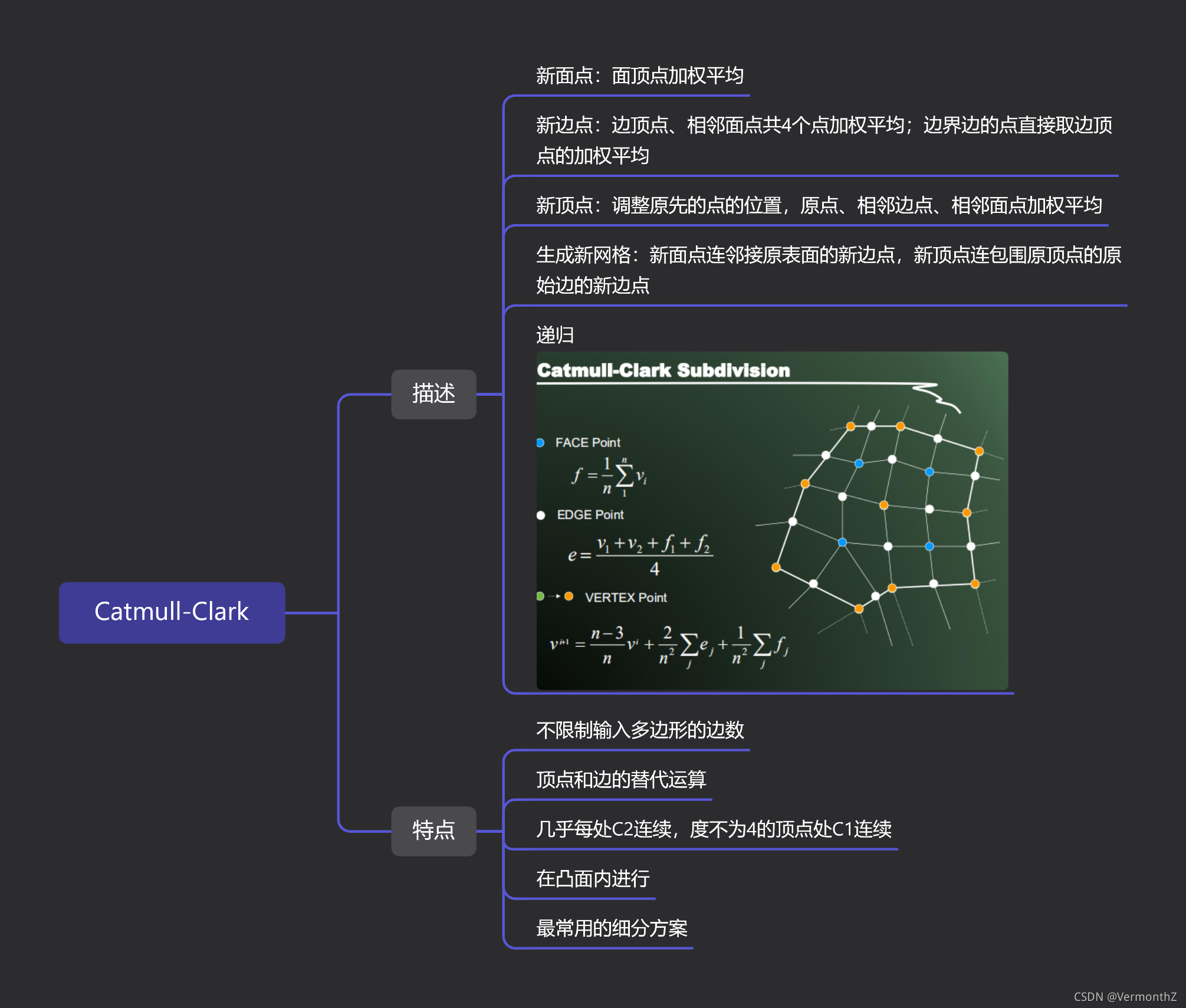
曲面细分需要有几何规则和拓扑规则，几何规则用于计算新顶点的位置，拓扑规则用于确定新顶点的连接关系。从作者的blog中我们推测Dust3D采用Catmull-Clark算法进行模型曲面的细分，引入了CGAL库中的Subdivision_method。Catmull-Clark细分是一种非常重要的网格细分法则，其可以对任意拓扑结构的多边形进行细分。

createIntermediateNode()

首先来看一个简单的插值函数。插值技术从我们一开始在计算机图形学课上接触时就已经感受到了它不可撼动的重要地位，它在曲线平滑、数字图像处理、计算机动画中有广泛应用。

void StrokeModifier::createIntermediateNode(const Node &firstNode, const Node &secondNode, float factor, Node *resultNode)
{
   
    float firstFactor = 1.0 - factor;
    //节点位置插值
    resultNode->position = firstNode.position * firstFactor + secondNode.position * factor;
    //插值得节点半径
    resultNode->radius = firstNode.radius * firstFactor + secondNode.radius * factor;
    //复制邻近节点的参数
    if (factor <= 0.5) {
   
        resultNode->originNodeIndex = firstNode.originNodeIndex;
        resultNode->nearOriginNodeIndex = firstNode.originNodeIndex;
        resultNode->farOriginNodeIndex = secondNode.originNodeIndex;
        resultNode->cutRotation = firstNode.cutRotation;
        resultNode->cutTemplate = firstNode.cutTemplate;
    } else {
   
        resultNode->originNodeIndex = secondNode.originNodeIndex;
        resultNode->nearOriginNodeIndex = secondNode.originNodeIndex;
        resultNode->farOriginNodeIndex = firstNode.originNodeIndex;
        resultNode->cutRotation = secondNode.cutRotation;
        resultNode->cutTemplate = secondNode.cutTemplate;
    }
}

subdivideFace2D()

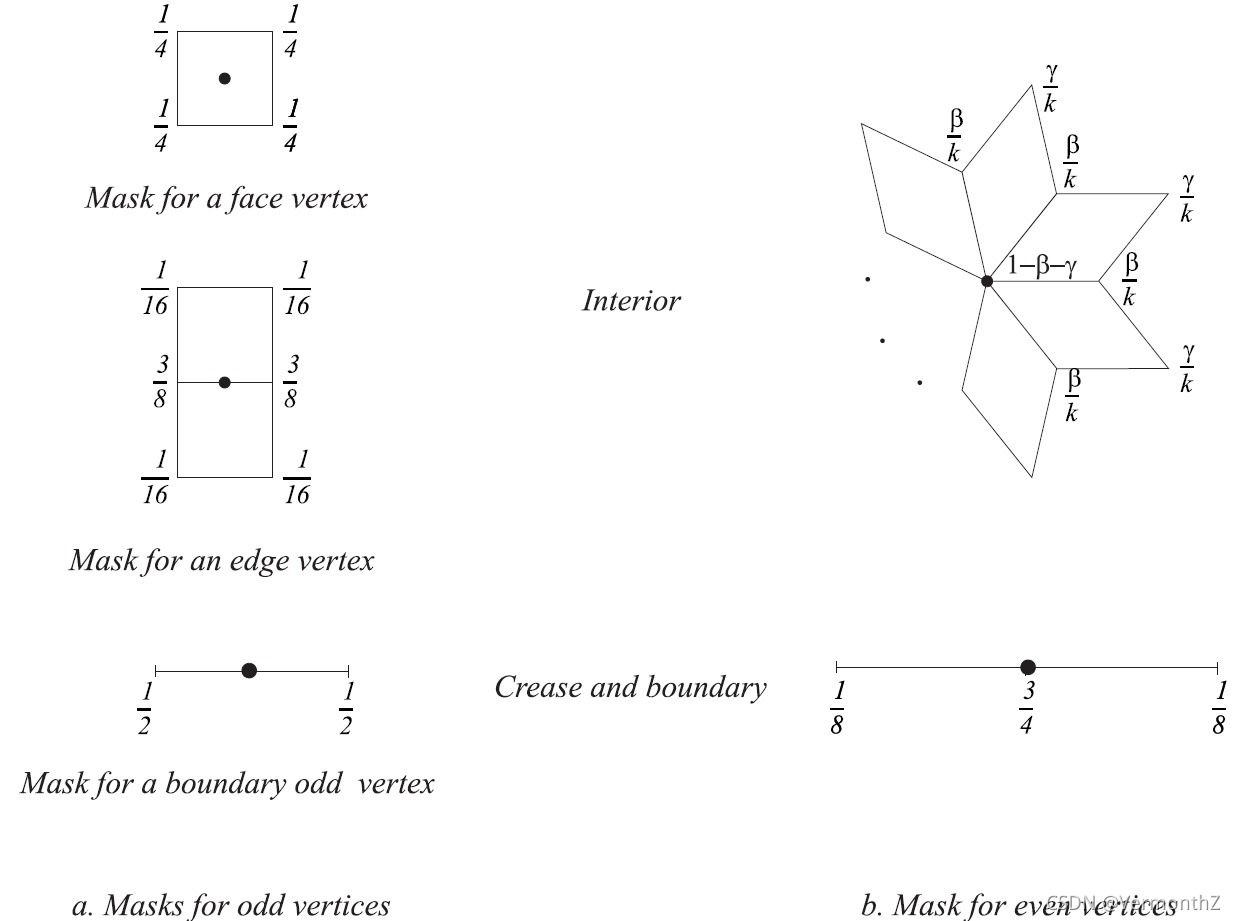
输入一个面，对于面上的每个点生成新面点和新边点：

• 新面点：原点与前后相邻的点三者加权平均，其中原点占最高的权重
• 新边点：原点与相邻的下一个点的平均

void subdivideFace2D(std::vector<QVector2D> *face)
{
   
    auto oldFace = *face;
    face->resize(oldFace.size() * 2);
    for (size_t i = 0, n = 0; i < oldFace.size(); ++i) {
   
        size_t h = (i + oldFace.size() - 1) % oldFace.size();
        size_t j = (i + 1) % oldFace.size();
        //新面点
        (*face)[n++] = oldFace[h] * 0.125 + oldFace[i] * 0.75 + oldFace[j] * 0.125;
        //新边点
        (*face)[n++] = (oldFace[i] + oldFace[j]) * 0.5;
    }
}

网格平滑

interpolateSegment()

对from到to进行分段的插值

void CentripetalCatmullRomSpline::interpolateSegment(std::vector<QVector3D>