平衡二叉树（ALV树）

一、AVL树简介

AVL树的名字来源于它的发明作者G.M. Adelson-Velsky 和 E.M. Landis。AVL树是最先发明的自平衡二叉查找树（Self-Balancing Binary Search Tree,简称平衡二叉树）。

平衡二叉树定义(AVL)：它或者是一颗空树，或者具有以下性质的二叉排序树：它的左子树和右子树的深度之差(平衡因子)的绝对值不超过1，且它的左子树和右子树都是一颗平衡二叉树。

平衡因子：将二叉树上某个节点的左子树高度减去右子树高度的值称为该节点的平衡因子BF(Balance Factor)。

二叉排序树基本概念

二、ALV树的平衡调整

定义结构体：

typedef struct Node
{
	int key;
	struct Node* left;
	struct Node* right;
	int height;
}BTNode;

1 获取平衡因子

//节点的高度
int height(BTNode* N){
	if (N == NULL)
		return 0;
	return N->height;
}

int getBF(BTNode* N){
	if (N == NULL)
		return 0;
	return height(N->left) - height(N->right);
}

2 对不平衡子树进行调整
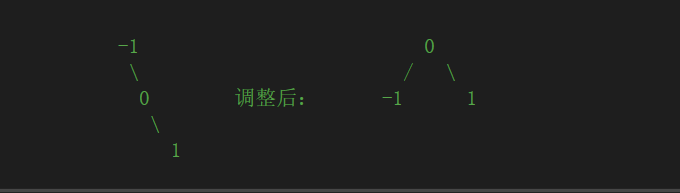
1）LL型
此时节点1不平衡（BF = 2-0 = 2 > 1）

把节点1作为实参，进行旋转，代码如下

BTNode* ll_rotate(BTNode* y){
	BTNode* x = y->left;
	y->left = x->right;
	x->right = y;

	y->height = max(height(y->left), height(y->right)) + 1;
	x->height = max(height(x->left), height(x->right)) + 1;

	return x;
}

2）RR型
此时节点-1不平衡（BF = 0-2 = -2 < -1）
在这里插入图片描述
把节点-1作为实参，进行旋转，代码如下

BTNode* rr_rotate(BTNode* y){
	BTNode* x = y->right;
	y->right = x->left;
	x->left = y;

	y->height = max(height(y->left), height(y->right)) + 1;
	x->height = max(height(x->left), height(x->right)) + 1;

	return x;
}

3）LR型
1的平衡因子 BF = 2-0 =2 > 1
先将1的左子树进行RR型旋转，再对1进行LL型旋转
在这里插入图片描述
4）RL型
1的平衡因子 BF = 0-2 =-2 < -1
先将1的右子树进行LL型旋转，再对1进行RR型旋转

三、删除节点操作

先删除节点，再进行平衡调整

//删除
BTNode* delNode(BTNode* root, int key){

	if (root == NULL)
		return root;

	if (key < root->key)
		root->left = delNode(root->left, key);

	else if (key > root->key)
		root->right = delNode(root->right, key);

	else {
		if ((root->left == NULL) || (root->right == NULL)) {
			BTNode* temp = root->left ? root->left : root->right;

			if (temp == NULL) {
				temp = root;
				root = NULL;
			}
			else
				*root = *temp;
			free(temp);
		}
		else {
			BTNode* temp = minValueNode(root->right);
			root->key = temp->key;
			root->right = delNode(root->right, temp->key);
		}
	}
	if (root == NULL)
		return root;

	root->height = max(height(root->left), height(root->right)) + 1;
	//平衡调整
	root = isBanlance(root);
	return root;
}

四、附上完整代码

#include<stdio.h>
#include<stdlib.h>

typedef struct Node
{
	int key;
	struct Node* left;
	struct Node* right;
	int height;
}BTNode;

int height(BTNode* N){
	if (N == NULL)
		return 0;
	return N->height;
}

int max(int a, int b){
	return (a > b) ? a : b;
}

BTNode* newNode(int key){
	struct Node* node = (BTNode*)malloc(sizeof(struct Node));
	node->key = key;
	node->left = NULL;
	node->right = NULL;
	node->height = 1;
	return node;
}

BTNode* ll_rotate(BTNode* y){
	BTNode* x = y->left;
	y->left = x->right;
	x->right = y;

	y->height = max(height(y->left), height(y->right)) + 1;
	x->height = max(height(x->left), height(x->right)) + 1;

	return x;
}

BTNode* rr_rotate(BTNode* y){
	BTNode* x = y->right;
	y->right = x->left;
	x->left = y;

	y->height = max(height(y->left), height(y->right)) + 1;
	x->height = max(height(x->left), height(x->right)) + 1;

	return x;
}

int getBF(BTNode* N){
	if (N == NULL)
		return 0;
	return height(N->left) - height(N->right);
}

BTNode* isBanlance(BTNode* root) {
	int balance = getBF(root);
	//printf("key:%d H:%d B:%d\n",root->key,root->height,balance);
	if (balance > 1 && getBF(root->left) >= 0) //LL型
		return ll_rotate(root);
	if (balance < -1 && getBF(root->right) <= 0) //RR型
		return rr_rotate(root);

	//LR型
	if (balance > 1 && getBF(root->left) < 0) {
		root->left = rr_rotate(root->left);
		return ll_rotate(root);
	}
	//RL型
	if (balance < -1 && getBF(root->right) > 0) {
		root->right = ll_rotate(root->right);
		return rr_rotate(root);
	}
	return root;
}

BTNode* insert(BTNode* node, int key){
	if (node == NULL)
		return newNode(key);

	if (key < node->key)
		node->left = insert(node->left, key);
	else if (key > node->key)
		node->right = insert(node->right, key);
	else
		return node;

	node->height = 1 + max(height(node->left), height(node->right));
	node = isBanlance(node);
	return node;
}
BTNode* minValueNode(BTNode* node) {
	while (node->left != NULL) {
		node = node->left;
	}
	return node;
}
BTNode* maxValueNode(BTNode* node) {
	while (node->right != NULL) {
		node = node->right;
	}
	return node;
}
BTNode* delNode(BTNode* root, int key){

	if (root == NULL)
		return root;

	if (key < root->key)
		root->left = delNode(root->left, key);

	else if (key > root->key)
		root->right = delNode(root->right, key);

	else {
		if ((root->left == NULL) || (root->right == NULL)) {
			BTNode* temp = root->left ? root->left : root->right;

			if (temp == NULL) {
				temp = root;
				root = NULL;
			}
			else
				*root = *temp;
			free(temp);
		}
		else {
			BTNode* temp = minValueNode(root->right);
			root->key = temp->key;
			root->right = delNode(root->right, temp->key);
		}
	}
	if (root == NULL)
		return root;

	root->height = max(height(root->left), height(root->right)) + 1;
	root = isBanlance(root);
	return root;
}

void inOrder(BTNode* root){
	if (root != NULL) {
		inOrder(root->left);
		printf("%d ", root->key);
		inOrder(root->right);
	}
}

int main()
{
	BTNode* root = NULL;
	root = insert(root, 7);
	root = insert(root, 5);
	root = insert(root, 10);
	root = insert(root, 0);
	root = insert(root, 6);
	root = insert(root, 11);
	root = insert(root, -1);
	root = insert(root, 1);
	root = insert(root, 2);
	printf("中序遍历：\n");
	inOrder(root);
	/* 
					 7
					/  \
				   1    10
				 /  \     \
				0    5     11
			   /    /  \
			  -1   2    6
	*/
	puts("\ndel:");
	root = delNode(root, 10);
	/* del 10
					   1
					 /   \
					0     7
				  /     /  \
				-1     5     11
					 /  \
					2    6
	*/
	inOrder(root);
	return 0;
}