求数组两个元素与(&)运算最大值，异或(^)运算最大值

摘要：本文首先解决的是数组中两元素与运算最大值问题，之后拓展异或运算最大值问题。建议读者顺序阅读，比较两问的相同与不同。

问题

给定一个数组 $A [n]$ ，求 $\ \& \ A[j])$ ，其中 $\ne j$ 。

分析

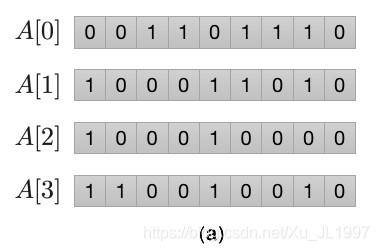
显然这道题目实际上是二进制运算问题。以下图(a)的数组为例：
在这里插入图片描述
对于&运算来说，相同位置上的数字同时为1，该位置运算结果才为1。

我们不妨从结果反推一下，假如最大值 $m a x$ 在第 $n$ 位上bit为1，则代表选中的两个元素在该位上的 bit 也为 1。如结果为 0101，则被选中的两个元素形式必定为 x1x1（x表示任意取值。）

为了确保结果值最大，我们希望选中的两个数字应该尽可能在高位&运算得到1。 所以我们从最高位开始我们的算法。

如图(b)，我们观察所有元素的最高位，显然，元素 $A [1], A [2], A [3]$ 在最高位进行 & 运算都能得到1。所以，假如存在最大值，最大值必然是这三个元素中的某两个元素计算得，我们不必考虑 $A [0]$ 和其他元素的组合，直接删掉 $A [0]$ 。
在这里插入图片描述
接下来考虑次高位，我们发现，在剩下的三个元素中，任意两个元素的 & 运算结果都为0，代表着最终结果 $m a x$ 在这一位上应该也为0。剩下元素的任何组合都不影响最终结果，可以任意取两个。

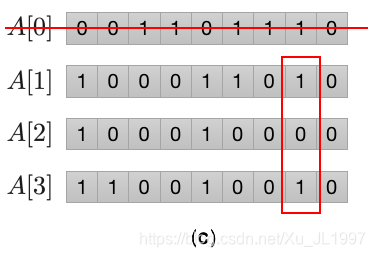
继续看后面的位。一直将算法应用到下图( c )的位置，此时，我们发现， $A [1], A [3]$ 在该位的 & 运算结果为1，而 $A [2]$ 与任何元素的运算结果都为0，所以，最大值必然是 $\& A[3])$ 。
在这里插入图片描述

解决方案

方法一：剔除元素至只剩两个

根据我们上面的观察，从最高位开始，假如当前位上存在两个元素可以 & 运算获得 1，我们可以将所有取值为 1 的元素保留下来，而取值为 0 的元素无论怎么运算都是 0，直接删除；假如当前位任何元素 & 运算都不能得到 0，我们就忽略这位，继续观察下一位。直到剩下两个元素，那么这两个元素 & 运算肯定是最大的。

算法流程：

初始化当前位为最高位
统计数组当前位上为 1 的元素的个数 count
假如 count 大于1，删除数组中该位为0的元素（大于 1 表示至少有两个元素该位取值为 1）
若数组剩下两个元素，返回两个元素的 & 运算结果。若当前位为最后一位，返回剩下任意两个元素的 & 运算结果。否则当前位取下一位，返回步骤2

方法二（改进版）：直接计算结果

算法一只要剩下两个元素就能够提前结束。但是每一轮循环结束都要检查当前数组剩下元素的个数，不太方便，我们可以稍微改进一下。

依然是统计1 的个数和剔除元素的思路，但是我们发现，每一次循环结束其实已经可以确定结果中的一位的取值了。所有循环结束，就能确定所有位。对 int 类型来说，32次循环就能确定结果的32位取值。

算法流程：

初始化当前位为最高位，初始化结果result为 0
统计数组当前位上为 1 的元素的个数 count
假如 count 大于1，删除数组中该bit为0的元素。同时，将result的当前位 bit 置 1
若当前位为最后一位，返回result。否则当前位取下一位，返回步骤2

两种方法的思路基本一致，其中方法二利用了结果与选中元素的关系，可直接计算结果，而不理会剩余元素的个数问题，更巧妙。

实现

怎么统计位上 1 的个数？

使用一个flag与数组元素进行 & 运算，如0x01可以判断最低位是不是1，使用位操作(<<)就能确定不同位上的取值是1还是0。

怎样剔除元素？

可以使用一个标记数组，标记被剔除/留下的元素。

下面是方法二的C/C++实现

unsigned Max(unsigned array[], int len){
    int maxBit = sizeof(unsigned) * 8; // 最高位数
    unsigned currBit = 1; // 当前位
    int mark[len]; // 标记被剔除元素的数组，下标对应相应的元素
    int result = 0;
    for (int i = 0; i < len; i++) mark[i] = 1; // 第i个元素为1，表示保留
    currBit = currBit << (maxBit-1);
    for (int i = 0; i < maxBit; i++){
        // 统计
        int count = 0;
        for(int j = 0; j < len; j++){
            if(mark[j] == 1 && (array[j] & currBit) != 0) 
            	count++;
        }
        
        if (count > 1){
            // 剔除
            for(int j = 0; j < len; j++){
                if ((array[j] & currBit) == 0)
                    mark[j]=0;  // 标记数组置为0表示剔除
            }
            // 更新结果，如 0100 + 0010 = 0110
            result += currBit;
        }
        // 下一位
        currBit = currBit >> 1;
    }
    
    return result;
}

拓展：求数组两个元素异或(^)运算最大值

题目改写为求两个元素的异或值。

我发现虽然两个题目背景很相似，可是上题的统计 1 个数的思路已经不适用了。

经查阅，网上大多数解法有两种，其一为构建前缀树(Trie)，其二为利用异或运算的公式。

前缀树(Trie)

其思路是利用数组中的每个元素二进制表示形式建一棵树，我看到网上大多数解法都开了太大的数组空间，不知道为什么，但是我觉得没有必要。
只要用现有的数组元素二进制值建一棵深度为33的树即可，从根到叶子结点的路径就代表了一个元素．然后再对数组中每一个元素取反之后到Trie中去搜索最大的异或值。
为什么要取反呢？
因为取反之后在查找Trie的时候如果当前匹配的话，那么就说明当前这一位异或之后是为１的，我们就可以继续沿着这个分支走下去．如果不匹配说明异或之后当前这位是为０，并且这个分支为空，所以我们只能走另外一个分支。
时间复杂度为 $\Theta(32 * n)$ ，也就是 $\Theta(n)$ 。

前缀树解法的原文：数组中两个元素异或求最大值

二进制异或运算

下面讨论第二种，对于二进制异或运算，我们有：

若a ^ b = c ，则 b ^ c = a 证明： a ^ b = c
两边同时 ^b 得，a ^ b ^ b = c ^ b
其中，b ^ b = 0，且 a ^ 0 = a
故 a = b ^ c

和上一题比较类似的是我们仍然可以从结果来反推选中的元素。假如最大值 $m a x$ 在第 $n$ 位上 bit 为1，则说明选中的两个元素在当前位的取值不同（0/1）。

我们仍然希望选中的两个数字应该尽可能在高位异或运算得到1，所以处理一下数组元素，每次只考虑高位，低位的bit设为0。

考虑二进制的前 1 位，其后的位设 0，如1101设为1000。根据我们的公式，我们可以假设 $m a x$ 当前位的值为 1，如 1000。取出处理过的数组中一个元素，如取出 $A [0]$ 为 1000。显然，如果 $m a x$ 当前位的值为 1，我们可以通过 $m a x * A [0]$ 计算出另一个元素的二进制肯定是 0000。之后在数组中寻找0000 即可。若找到则说明我们的假设成立了， $m a x$ 的当前位确实为 1。
如果没有找到 0000，我们可以取出下一个元素 $i$ ，继续通过 $m a x * i$ 计算出对应元素的二进制，查找。
直到所有的元素都取出一遍，若都没有找到对应的一对元素，说明假设不成立， $m a x$ 当前位为 0。其本质是没有一对元素可以通过异或运算得到我们假设的 $m a x$ ，故假设应该摒弃。

考虑二进制的前 2 位，其后的位设 0，如1101设为1100。此时当前位挪到第 2 位， $m a x$ 第 1 位的取值已经在上一步得到。同样假设 $m a x$ 当前位为1，如 1100，取出处理后数组的一个元素，计算可能存在的对于元素，查找，判断假设是否成立。成立就 break，不成立就继续取下一个元素，以此类推。可以得到 $m a x$ 前 2 位的取值。

考虑二进制的前 3 位 …

当所有位都考虑完， $m a x$ 的结果也可以直接得出了。

实现思路：处理数组，只考虑前 n 位 $\to$ 取元素，计算另一元素取值 $\to$ 查找

下面是实现的Java代码：

int findMaximumXOR(int[] nums) {
	int len = nums.length;
    if(len < 2) return 0;
    
    int max = 0;
    int flag = 0;
    for (int i = 31; i >= 0; i--){
    	HashSet<Integer> hash = new HashSet<>();
    	// 获取处理后的数组，存在hash集合中
        flag = flag | (1 << i);
        for(int num: nums) 
        	hash.add(num & flag); // &运算将低位bit置0
		// 查找集合中是否存在计算出来的元素
        int temp = max | (1 << i); // 假设值为temp
        for (int num: hash) {
            if (hash.contains(num ^ temp)) {
                max = temp;
                break;
            }
        }
    }
    return max;
}

总结

异或最大值的两种算法的时间复杂度都是 $\Theta(n)$ ，都是利用空间换时间。第一种方法构造前缀树（字典树）自不用说，第二种方法也是巧妙地利用了 hash 查找 $\Theta(1)$ 时间开销的特点。

本文结束，欢迎留言讨论。