📑前言

循环神经网络（RNN）是深度学习中的一种重要模型，特别适用于处理序列数据，如时间序列预测、自然语言处理（NLP）等。本文将详细介绍RNN的基本结构、长短期记忆网络（LSTM）以及门控循环单元（GRU），帮助读者更好地理解和应用这些模型。

一、循环神经网络的基本结构

循环神经网络（RNN）与传统的前馈神经网络（如多层感知器和卷积神经网络）不同，RNN具有内存能力，能够在处理当前输入时保留之前的信息。这使得RNN特别适合处理序列数据，如文本、语音和时间序列等。

1.1 RNN的基本单元

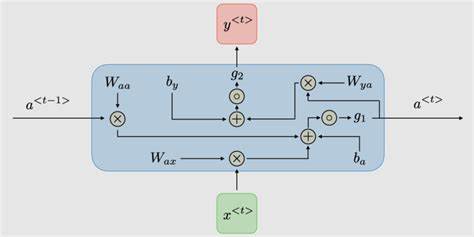
RNN的基本单元包括输入层、隐藏层和输出层。隐藏层不仅接收当前时间步的输入，还接收前一时间步的隐藏状态。这种结构使得RNN能够保留之前的输入信息，并在处理当前输入时考虑之前的上下文。
以下是一个RNN单元的数学表达式：
$h_t=\sigma (W_h\cdot h_{t-1}+W_x\cdot x_t+b)$
其中，$h_t$是当前时间步的隐藏状态，$h_{t-1}$是前一时间步的隐藏状态，$x_t$是当前时间步的输入，$W_h$和$W_x$是权重矩阵，$b$是偏置，$\sigma$是激活函数（如tanh或ReLU）。

1.2 RNN的前向传播

在前向传播过程中，RNN通过隐藏状态的递归计算，将序列数据逐步传递到网络的每一个时间步。具体步骤如下：

1. 初始化隐藏状态$h_0$（通常为零向量）。
2. 对于每一个时间步$t$，计算当前隐藏状态$h_t$。
3. 利用最后一个时间步的隐藏状态$h_T$或每一个时间步的隐藏状态$h_t$进行输出预测。

RNN的这种结构能够捕捉序列数据中的依赖关系，但也存在一些问题，如梯度消失和梯度爆炸。

1.3 RNN的梯度消失和梯度爆炸问题

在训练RNN时，梯度通过时间步反向传播（BPTT）进行更新。然而，当序列较长时，梯度可能会变得非常小（梯度消失）或非常大（梯度爆炸），导致训练过程中的不稳定性。为了解决这一问题，研究者提出了长短期记忆网络（LSTM）和门控循环单元（GRU）。

二、长短期记忆网络（LSTM）

长短期记忆网络（LSTM）是一种特殊的RNN，通过引入门控机制来解决梯度消失和梯度爆炸问题。LSTM能够在较长的时间序列中保留重要信息，从而提高模型的性能。

2.1 LSTM的基本结构

LSTM单元由一个记忆细胞（Cell State）和三个门控单元（输入门、遗忘门和输出门）组成。这些门控单元通过控制信息的流动，帮助LSTM选择性地保留或丢弃信息。

输入门（Input Gate）

输入门控制当前输入信息是否被加入到记忆细胞中。其数学表达式为：
$i_t=\sigma (W_i\cdot [h_{t-1},x_t]+b_i)$
其中，$i_t$是输入门的输出，$W_i$是权重矩阵，$b_i$是偏置，$\sigma$是激活函数。

遗忘门（Forget Gate）

遗忘门控制记忆细胞中哪些信息需要被丢弃。其数学表达式为：
$f_t=\sigma (W_f\cdot [h_{t-1},x_t]+b_f)$
其中，$f_t$是遗忘门的输出，$W_f$是权重矩阵，$b_f$是偏置，$\sigma$是激活函数。

输出门（Output Gate）

输出门控制记忆细胞中哪些信息需要被输出。其数学表达式为：
$o_t=\sigma (W_o\cdot [h_{t-1},x_t]+b_o)$
其中，$o_t$是输出门的输出，$W_o$是权重矩阵，$b_o$是偏置，$\sigma$是激活函数。

2.2 LSTM的前向传播

在前向传播过程中，LSTM通过以下步骤更新记忆细胞和隐藏状态：

1. 计算遗忘门$f_t$，决定哪些信息需要被丢弃。
2. 计算输入门$i_t$和新的候选记忆${\tilde{C}}_t$，决定哪些新信息需要被添加到记忆细胞中。
3. 更新记忆细胞$C_t$：

$C_t=f_t\cdot C_{t-1}+i_t\cdot {\tilde{C}}_t$

4. 计算输出门$o_t$，决定哪些信息需要被输出。
5. 更新隐藏状态$h_t$：

$h_t=o_t\cdot \tanh (C_t)$
LSTM通过这些步骤，能够有效地保留长时间序列中的重要信息，从而提高模型的性能。

2.3 LSTM的优势

LSTM相较于传统RNN，具有以下优势：

1. 解决梯度消失和梯度爆炸问题：通过引入门控机制，LSTM能够有效控制信息流动，避免梯度消失和梯度爆炸。
2. 捕捉长时间依赖关系：LSTM能够在长时间序列中保留重要信息，从而更好地捕捉长时间依赖关系。
3. 灵活性：LSTM的结构使其能够灵活地处理不同类型的序列数据，如文本、语音和时间序列等。

三、门控循环单元（GRU）

门控循环单元（GRU）是另一种解决RNN梯度消失和梯度爆炸问题的模型。GRU相比LSTM，具有更简洁的结构，但仍能有效保留序列中的重要信息。

3.1 GRU的基本结构

GRU单元由两个门控单元（重置门和更新门）组成。这些门控单元通过控制信息的流动，帮助GRU选择性地保留或丢弃信息。

重置门（Reset Gate）

重置门控制当前输入信息与前一时间步的隐藏状态结合的程度。其数学表达式为：
$r_t=\sigma (W_r\cdot [h_{t-1},x_t]+b_r)$
其中，$r_t$是重置门的输出，$W_r$是权重矩阵，$b_r$是偏置，$\sigma$是激活函数。

更新门（Update Gate）

更新门控制记忆细胞中的信息保留和丢弃的程度。其数学表达式为：
$z_t=\sigma (W_z\cdot [h_{t-1},x_t]+b_z)$
其中，$z_t$是更新门的输出，$W_z$是权重矩阵，$b_z$是偏置，$\sigma$是激活函数。

3.2 GRU的前向传播

在前向传播过程中，GRU通过以下步骤更新记忆细胞和隐藏状态：

1. 计算重置门$r_t$，决定前一时间步的隐藏状态$h_{t-1}$对当前候选隐藏状态${\tilde{h}}_t$的影响。
2. 计算候选隐藏状态${\tilde{h}}_t$：

${\tilde{h}}_t=\tanh (W\cdot [r_t\cdot h_{t-1},x_t]+b)$

3. 计算更新门$z_t$，决定记忆细胞中的信息保留和丢弃的程度。
4. 更新隐藏状态$h_t$：

$h_t=z_t\cdot h_{t-1}+(1-z_t)\cdot {\tilde{h}}_t$
GRU通过这些步骤，能够有效地保留长时间序列中的重要信息，从而提高模型的性能。

3.3 GRU的优势

GRU相较于传统RNN和LSTM，具有以下优势：

1. 简洁的结构：GRU的结构相比LSTM更为简洁，只有两个门控单元，计算效率更高。
2. 解决梯度消失和梯度爆炸问题：GRU通过引入门控机制，能够有效控制信息流动，避免梯度消失和梯度爆炸。
3. 性能优越：在一些任务中，GRU的性能可以与LSTM相媲美，甚至超越LSTM。

四、小结

循环神经网络（RNN）是处理序列数据的强大工具，然而其梯度消失和梯度爆炸问题限制了其应用。为了解决这些问题，长短期记忆网络（LSTM）和门控循环单元（GRU）被引入，它们通过门控机制有效地保留序列中的重要信息，显著提高了模型的性能。理解RNN、LSTM和GRU的基本结构和工作原理，是深度学习研究者和开发者的必备技能。希望本文能帮助读者更好地理解和应用这些模型，在实际项目中取得更好的效果。