滚动轴承信号分析

第一章 滚动轴承常见故障及其基本模型

前言

滚动轴承作为现代机械中广泛使用的部件之一，由于其主要部件之间的滚动关系使得其成为机械中最易受损的元件，因此滚动轴承的故障诊断研究非常重要。振动检测法是最有效的诊断方法，本文主要针对振动信号特征、故障特征频率、振动信号与线性调频信号之间的关系及振动信号拟合进行分析和讨论。

提示：以下是本篇文章正文内容，下面案例可供参考

一、滚动轴承常见的故障模式

滚动轴承的故障模式${}^{[1]}$分为正常故障模式和非正常故障模式，正常故障模式通常是指轴承的安装、润滑及维护良好的情况下，内外圈或滚动体遭到点蚀损坏。这是由于重复受到大量变化的应力导致的。轴承因点蚀而损坏时，在运行过程中通常会产生强烈的振动、噪声和热量。非正常故障模式是指由于轴承安装不当、润滑和维护不良引起的其他故障模式。例如，当润滑油不足时，轴承烧伤，润滑不良导致轴承表面直接接触或异物掉落导致过度接触，轴承因装配不当而损坏，内圈破损，内外圈和保持架被挤碎。这些故障模式虽然是多种多样，但是都可以通过适当的方法避免，并且也不能根据这些故障模式来建立轴承的计算公式。由于疲劳造成点蚀破坏的这种正常故障模式，可以通过振动信号监测，及时检测出故障，从而尽快替换故障的轴承。
滚动轴承在工作过程中会产生振动、噪声和热的主要因素有:外部激励和自身原因。其中外部激励主要包括不平衡、失调、流体激振、共振等原因。而自身原因产生振动的原理及特征如下:
(1)随着滚动体位置的改变，其所承受的载荷也会发生变化，由此引起的振动频率跟滚珠个数及保持架转速有关。
(2)滚道表面和滚动体表面的粗糙程度也会引起轴承振动，由此产生的激励会使得轴承产生各部件的固有振动，如径向弯曲振动、轴向弯曲振动
(3)滚动体尺寸不均匀，内圈和外圈偏离中心而引起振动，其振动频率包含轴的转频分量及倍频分量。
(4)如果润滑油不足或含有杂质，会引起摩擦和振动。其中摩擦包含滚动体与滚道的滚动摩擦、滚动体与保持架的滑动摩擦，而这些摩擦会引起轴承元部件的磨损、划伤、剥落、裂纹等，产生大量的热，导致轴承材料胶合、噪声和振动。
(5)当轴承装歪或转轴发生弯曲会导致轴承变形，会产生振动。以振动信号频率中的转频为特性，同时具有滚动体的频率特征。
(6)滚道中心接触面发生局部缺陷会产生振动，包括如工作表面的剥落、裂痕、腐蚀及胶合等。

二、滚动轴承振动信号的特征

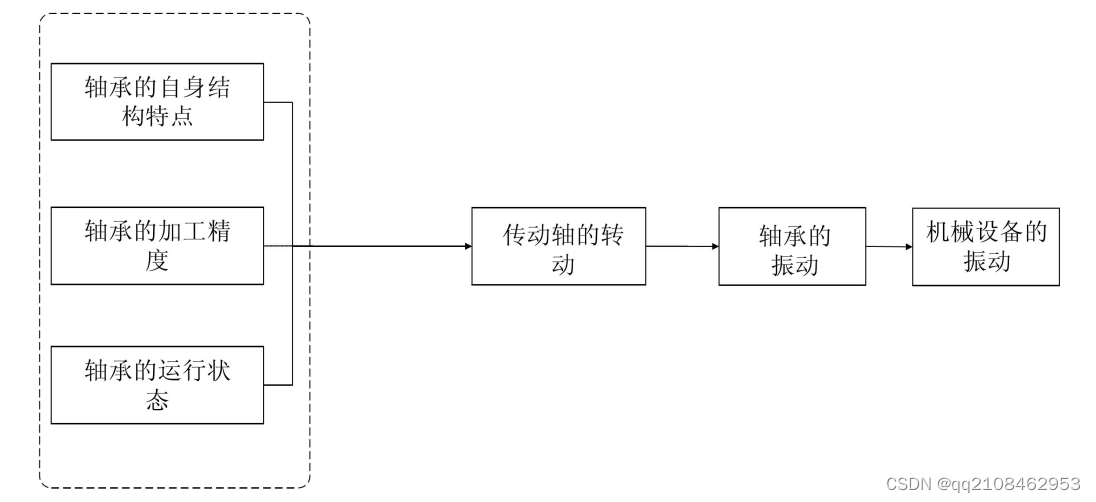
滚动轴承是利用轴承座固定底部，内圈与传动轴过盈配合，使二者以同一速率转动，由电机带动传动轴转动，而传动轴随轴承同时转动，从而产生了振动。如下图所示，滚动轴承在运行过程中产生振动的主要有三个因素: - - -是由于轴承自身的结构引起的振动为其固有性质，跟轴承是否发生故障没有直接关系。另一方面，由于加工精度引起的振动，轴承的振动是由于加工精度低或装配误差大造成的。最后就是由于轴承的工作状态所引起的振动，当轴承出现异常情况，如点蚀，断裂等，都会产生振动，这种情况有可能导致严重的后果。

滚动轴承的固有频率

当滚动轴承与传动轴一起旋转时，滚动体与内外圈碰撞使轴承部件振动。若能在一定频率范围内振动，则认为该振动为正常振动，其频率称为固有频率${}^{[2]}$。固有频率只与轴承本身的材料、质量及形状有关，而与传动轴的转速无关。滚动轴承在转动过程中，不同的元件其固有频率不同，默认滚动轴承的材料为钢材，滚动体为钢球，其具体关系如下:
滚动体的固有频率:
$$f_{ball}=\frac{0.848}{d}\sqrt{\frac{E}{2\rho }}(1)$$

式中: d为滚动体半径(m)，ρ为材料密度$(kg/m^3)$，E为滚动体的弹性模量$(N/m^3)$。
内、外圈的固有频率:

$$f_n=\frac{n(n^2-1)}{2\pi }\underline{\text{x}}\frac{4}{D^2}\sqrt{\frac{EIg}{\gamma A}}(2)$$

式中: n为振动阶数，n=2,3…; E为弹性模量，其中钢材的弹性模量为210Gpa;I为轴承圈的横截面所受的惯性矩($m{m}^2$);γ为钢材的密度，–般钢材的密度为$7.86x10^{-5}kg/m{m}^3$，A为轴承圈的横截面积$(m{m}^2)$，D为轴承的节径(mm)，g为重力加速度取$9800mm/s^2$。将上述的已知参数代入式(2)中，简化可得:
$$f_{(I,O)}=9.40\underline{\text{x}}\frac{h}{D^2}\underline{\text{x}}\frac{n(n^2-1)}{\sqrt{n^2+1}}(3)$$
其中: h为圆环的厚度(mm)，D为轴承的节径(mm)。
滚动轴承中各个元件的固有频率受到其安装状态的影响而发生变化，如式(2)、(3)为 其处于自由状态时的固有频率计算公式。而对于滚动体来说，其固有频率是很高的，以至于一般的测量装置无法测出固有频率的范围。因此，在故障诊断中，经常用到的是其内圈和外圈的固有频率，而很少考虑滚动体的固有频率。
根据_上述分析，可得出结论，滚动轴承的固有频率只与轴承自身的材料、尺寸和结构有关，而与传动轴旋转速度无关。

滚动轴承的故障特征频率

滚动轴承在随传动轴转动的过程中，当轴承的某部分元件出现了故障损伤点时，其每随轴转动一圈都会与其他的零部件发生周期性的碰撞，从而产生冲击振动。一般来说，这种脉冲波称为冲击脉冲，而其对应的频率称为故障特征频率${}^{[3]}$。由于故障特征频率较低且有规律，因此可以根据轴承的一些参数求出其对应元件的故障特征频率。在故障诊断的过程中，轴承的故障特征频率相对于其固有频率更具有检测的意义。

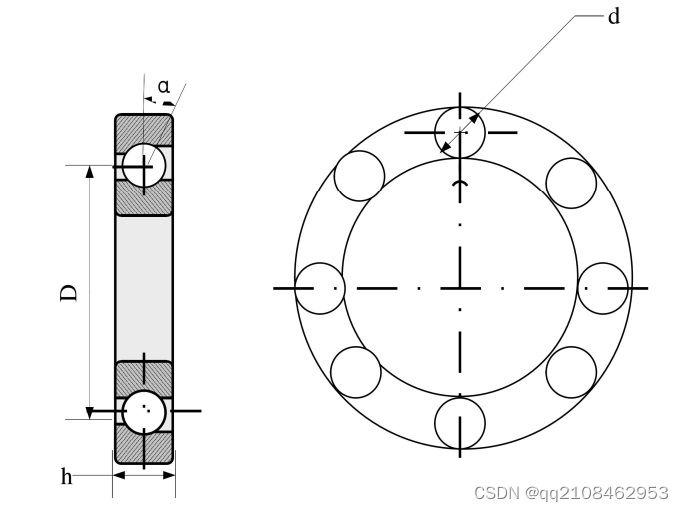
当滚动轴承失效时，损伤点周期性地与其他部件碰撞，导致轴承系统周期性自由衰减振荡，该冲击频率称为故障特征频率，不同的轴承具有不同的故障特征频率。设轴承外圈固定不动，内圈随轴旋转。电机带动轴承转速为n r/min,则内圈随轴旋转的转动频率为$f_n=n/60$，轴承节圆直径为D(mm),滚动体直径为d(mm)，接触角为a(°), 滚动体个数为m。滚动轴承的特征参数示意图，如上图所示，其故障特征频率的理论计算公式如下:
(1)滚动轴承内圈故障特征频率:
$$f_i=\frac{1}{2}m{f}_n(1+\frac{d}{D}\cos \alpha )(4)$$

(2)滚动轴承外圈故障特征频率:
$$f_o=\frac{1}{2}m{f}_n(1-\frac{d}{D}\cos \alpha )(5)$$

(3)
滚动轴承滚动体故障特征频率:
$$f_{b}all=\frac{1}{2}{f}_n(1-(\frac{d}{D}\cos \alpha {)}^2)\frac{D}{d}(6)$$

4)滚动轴承保持架故障特征频率:
$$f_{bao}=\frac{1}{3}{f}_n(1-(\frac{d}{D}\cos \alpha ))(7)$$
由式(4)至(7)可以看出，滚动轴承中不同的元件发生故障，其故障特征
频率也会随之改变。一般情况下，判断轴承是否发生故障的依据是根据其故障特征频率的幅值是高还是低来判定。幅值越高，越能说明轴承可能或已经存在了故障。通常，可以利用滚动轴承振动信号的频谱图中是否出现谱峰来判断轴承故障。但在实际应用的过程中，由于轴承安装情况，尺寸精度等因素都会导致滚动体不会单纯的做滚动运动，因此频谱峰值处的频率与理论上计算出的频率值会出现误差。
由于上述原因的存在，使得在通过频谱图获取故障特征频率时，需要找到故障特征频率理论计算值的邻域内的近似值来判断轴承是否发生故障。上述公式都是针对单一滚动体和单一处损伤的频率，在实际计算中，滚动体有很多个，其故障点也不会只有一个，因此，其故障分析不能单纯依靠频谱来进行故障分析。可以通过分析故障特征频率的变化趋势，从而分析其故障，通过建立故障特征频率的模型，找出振动信号与线性调频信号的内在关系，从而找出适用的故障分析方法。

振动信号拟合模型的建立

传动轴的转动激励为轴承正常运行时的主要振动源，其主要成分为其转动频率分量，可以表示为:
$$x(t)=\sum _{m=0}^M{x}_m\sin (2\pi f_{n}mt+{\phi }_m)(8)$$

其中:x(t)为振动信号的时域表达式，$x_m$为第m阶转动频率谐波分量的幅值，${\phi }_m$为第m阶转动频率谐波分量的相位，$f_n$ 为传动轴的转动频率，M为滚动体的个数。
如果滚动轴承仅受到–处损坏，则其振动信号的幅度和频率会发生变化，此时，损伤点的故障特征频率为中心频率，旋转轴的传动频率为调制边带，并且可以从信号中提取调制信息。为了分析由故障频率的变化趋势，可以将具有损伤点的滚动轴承振动信号模型为:
$$\begin{gathered} x(t)=\sum _{m=0}^M{x}_m[1+\sum _{n=0}^N{A}_{m,n} \\ \sin (2\pi f_{z}nt+{\alpha }_{m,n})]\sin (2\pi f_{n}mt+{\phi }_m)(9) \end{gathered}$$

式中: $A_{m,n}$是幅值调制函数的第n阶分量的振幅，${\alpha }_{m,n}$ 是幅值调制函数第n阶分量的相位，f_z$是故障点所在位置的故障特征频率。
将式(9)使用带通滤波抑制其谐波分量，使其相位为零，则其输出的模型可简化为:
$$\begin{gathered} x(t)=x_m[1+A_{m,1}\sin (2\pi f_{z}t)]\sin (2\pi f_{n}mt) \\ =M\sin (2pi{f}_{z}t)\sin (2f_{n}mt)+N\sin (2\pi f_{n}mt)(10) \end{gathered}$$

其中: $M=x_m{A}_{m,1},N=x_m$。式(10)为存在单一损伤点的滚动轴承的振动信号模型。当滚动轴承的某个零件部位出现损伤点，如点蚀或磨损的故障时，会导致轴承节圆的直径D发生改变，从而导致$f_z$发生变化，通常默认$f_z$随时间t呈线性变化，即故障特征频率随时间呈线性变化的线性调频信号，$f_z$随时间t的变化模型如式(11)所示。
$$f_z=f_0+kt(11)$$

其中:$f_0$故障频率的初始频率，k为故障频率随时间变化的斜率。式(10)可以表示为式(12)，即为具有单损伤点和线性调频特性的滚动轴承振动信号模型。
$$x(t)=M\exp (j\pi k{t}^2+j2\pi f_{0}t)\sin (2\pi f_{n}mt)+N\sin (2\pi f_{n}mt)(12)$$

参考文献

[1] 濮良贵,陈国定,吴立言，等.机械设计第九版[M].北京:高等教育出版社,2013:313-315.
[2]张磊.滚动轴承的振动检测及故障诊断系统研制[D].沈阳:沈阳理工大学，2018: 11-12.
[3]郭艳平，解武波，龙涛元.拟合故障振动信号模型实现滚动轴承故障诊断[J].机械设计与制造，2017(11): 205-208.