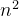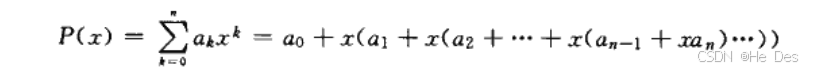插入排序与霍纳规则

参考书：机械工业出版社《算法导论》第二版

插入排序

插入排序来自扑克牌的灵感，每次抽牌都要从洗好的牌堆里抽一张，然后与自己现有的牌比较，插入到合适的位置

算法步骤

由此可以看到，插入排序时对元素进行这样一种操作：

1 拿到元素

2 与已排序的序列逐一比较

3 插入到合适的位置

4 拿到下一个元素

5 循环直到未排序元素为空

根据这样的描述我们可以写出插入排序的代码

void insertion_sort(int arr[],int len){
	for(int i =1;i<len;i++){
		int key=arr[i];					//key是要比较的元素 
		int j=i-1;		
		while(j>=0 && arr[j]>key){		//该数组左部是已排序的，右部亟待排序 
			arr[j+1]=arr[j];		
			j--; 
		}
		arr[j+1]=key;					
	}
}

解释：只利用一个数组完成插入排序，就把数组分为已排序和未排序两个部分，一个指针i指向此时要进行插排的元素，自此元素的左方第一个元素一直向左比较直到遇到不大于他的数然后退出while循环，最后完成交换值，进入下一轮for循环

从代码和文字描述都可以看出，插排的平均复杂度是

插入排序具有很好的稳定性（ps：排序算法的稳定性指排完序后改变原来元素顺序应该尽量少）

二分优化

在插入排序中牺牲时间复杂度的关键是在查找不大于他的元素时，查找方法是逐一查找，也就是遍历未排序元素花费了n的时间，对每个未排序元素又查找对应位置，总共花费就是nxn

而对于查找这一过程，可以使用二分查找来优化查找过程至对数级

应用了二分查找的插入排序也叫折半插入排序

源码：

void insertion_sort(int arr[], int len) {
  if (len < 2) return;
  for (int i = 1; i != len; ++i) {
    int key = arr[i];
    auto index = upper_bound(arr, arr + i, key) - arr;
    // 使用 memmove 移动元素，比使用 for 循环速度更快，时间复杂度仍为 O(n)
    memmove(arr + index + 1, arr + index, (i - index) * sizeof(int));
    arr[index] = key;
  }
}

补充：

uupper_bound函数

定义在algorithm库内

这个函数底层通过二分查找实现，目的是找到大于目标值的第一个元素

声明为：

ForwardIterator upper_bound (ForwardIterator first, ForwardIterator last,const T& val，Compare comp);

函数返回一个正向迭代器，查找成功返回指向该元素的迭代器，否则返回last

comp是一个接受两个参数返回bool类型的比较规则，不写默认目的是找到大于目标值的第一个元素

STL库中upper_bound的实现：

1. template <class ForwardIterator, class T>
2. ForwardIterator upper_bound (ForwardIterator first, ForwardIterator last, const T& val)
3. {
4. ForwardIterator it;
5. iterator_traits<ForwardIterator>::difference_type count, step;
6. count = std::distance(first,last);
7. while (count>0)
8. {
9. it = first; step=count/2; std::advance (it,step);
10. if (!(val<*it)) //  if (!comp(val,*it)), 对应第二种语法格式
11. { first=++it; count-=step+1; }
12. else count=step;
13. }
14. return first;
15. }

memmove函数

声明为

void* memmove(void* dest, const void* src, size_t n)

主要功能是将源内存块的数据复制到目标内存块，即使源和目标内存区域重叠。

霍纳规则

计算多项式的一种简易算法

比起一项一项的计算，霍纳规则是：

也就是每次都提出来公因数x，这样只存储每项的系数，计算时只需要前一项系数乘以x减去该项系数即可

例如式 $p(x)=2x^4-x^3+3x^2+x-5$

系数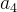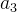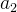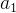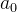
	2	-1	3	1	-5
x=1	2	2*1-(-1)=3	-1*1-3=-4	-4*1-1=-5	-5*1-（-5）=0

p(x=1)的值即使最右下表格内的得数为0