导入

前缀和 相信大家都知道，它可以用来求区间和。

可是前缀和不怎么灵活，如果要对某个点进行修改，那就需要更新前缀和数组的所有下标不小于修改位置的元素的值，算法复杂度最高可达 $O(n)$，速度十分缓慢，如果碰到大量修改，会直接歇菜。

为了加快单点修改的速度，树状数组就诞生了！

什么是树状数组

树状数组或二叉索引树（英语：Binary Indexed Tree），又以其发明者命名为Fenwick树，最早由Peter M. Fenwick于1994年以A New Data Structure for Cumulative Frequency Tables为题发表在SOFTWARE PRACTICE AND EXPERIENCE。其初衷是解决数据压缩里的累积频率（Cumulative Frequency）的计算问题（当我没说），现多用于高效计算数列的前缀和， 区间和。

以上内容来自网络。

如果你看完了上一段，那么恭喜你！浪费了10秒钟。

树状数组支持以下两种操作，

• 单点修改。
• 区间和查询。

两种操作的时间复杂度都为 $O(logn)$。

树状数组的构造

树状数组的思想大概是这样的，我们可以为数组维护多个区间，在查询和修改时，对这几个包含该点或区间的区间进行修改和查询。

可这些区间也不能随便设置，不然在进行查询修改时，如果包含区间的区间过多，那也会导致速度缓慢。

好了，不扯这些废话了，先来看看它长什么样吧。

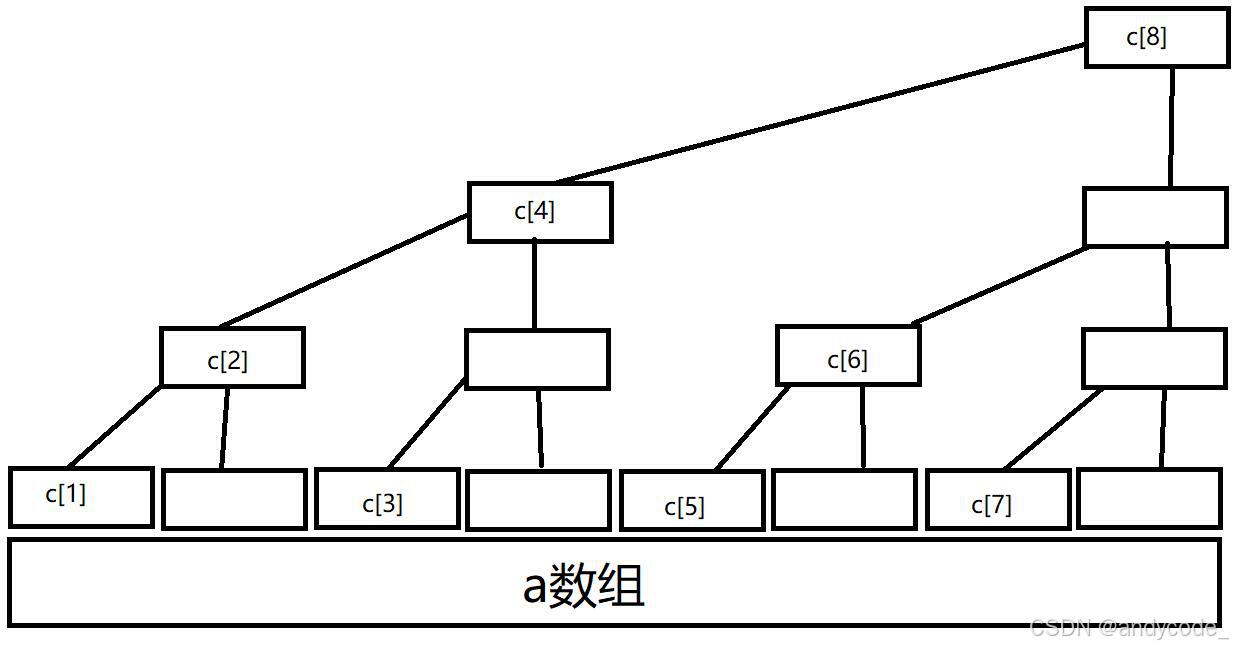
设一个长度为 $n$ 的树状数组 $c_i$，那它的元素维护的区间是这样的。

其中 $c_i$ 就等于 $a$ 数组 $[i-lowbit(i)+1,i]$ 的区间和。

$lowbit(i)$ 是什么呢？$lowbit(i)$ 指的是 $i$ 在二进制下最后一个的为 $1$ 的哪一位所代表的值。比如当 $i=10$，即 $(1010{)}_2$ 时，最后一个为 $1$ 的二进制位为从右往左第二位，所以 $lowbit(i)=(10{)}_2=2$。

lowbit的实现方法

$lowbit(x)$ 的实现方法如下:

int Lowbit(int x){
	return x&(-x);
	//十分简洁，算法复杂度为 O(1)
}

为什么是 x&(-x) 呢？

大家应该都知道二进制的原码、反码、补码。当 $x$ 为负数时，他的二进制就是用补码来表示。即将 $x$ 包括符号位取反后加 $1$。

而将 $x$ 变成负数后，二进制在运算时就会变成补码。因为 $lowbit(x)$ 是最后一个为 $1$ 的二进制位，所以它后面所有的二进制位都为 $0$，取反后自然为 $1$，$lowbit(x)$ 的那一位则会变成 $0$，加 $1$ 后，$lowbit(x)$ 后面的二进制位会一直进位到 $lowbit(x)$ 这一位，并全部变为 $0$。所以 $lowbit(x)$ 的后面的二进制位进行按位与后都为 $0$。而 $lowbit(x)$ 前面的二进制位因为取反，且加 $1$ 时没有被影响的原因，按位与时都是 1&0 或 0&1，答案自然为 $0$。而只有 $lowbit(x)$ 的那一位在变成补码时仍和原来一样，都为 $1$，按位与后就只剩它了。所以答案一定为 $lowbit(x)$。

如果前面那一大坨文字还是令你有些困惑，那我们可以来举一个例子。

设 $x$ 为 $26$，则二进制表达下为 $(11010{)}_2$，很容易看出 $lowbit(x)=(10{)}_2=2$。我们再用之前的方法验证一下，$-x$ 取反后为 $(00101{)}_2$，加 $1$ 后为 $(00110{)}_2$。和 $x$ 按位与后，结果为 11010&00110=2，结果仍为 $2$。

如果你还是不懂的话，也可以这么写。

int Lowbit(int x){
	int cnt=0;
	while(!(x&1))
		x>>=1,cnt++;//统计lowbit后有多少0
	return 1<<cnt;//返回lowbit的值，即2的cnt次方
	//略微慢些，算法复杂度为 O(log n)
}

因为可能要遍历 $x$ 的所有二进制位，所以时间复杂度为 $O(logn)$。虽然慢了点，但也没什么大碍。

树状数组求区间和

方法

知道了树状数组的形成，那通过树状数组如何进行区间和查询呢？

设要求区间 $[l,r]$ 之和，那我们可以先对他进行类似前缀和的转换。将它转化成区间 $[1,r]$ 之和，减区间 $[1,l-1]$ 之和（$[1,0]$ 的区间和为 $0$）。

这样我们只需要求前 $x$ 个数的和就行了。

看了树状数组的构造的朋友们应该能看出，$c_i$ 维护的区间的右端点为 $i$，所以我们在寻找前缀时，只需将 $c_x$ 加上前 $x-lowbit(x)$ 个数的和（因为 $c_x$ 只涵盖了区间 $[x-lowbit(x)+1,x]$），一直到 $x$ 为 $0$ 为止，递归/递推即可。

代码如下：

int Sum(int x){
	if(x==0)
		return 0;//如果x=0，返回0并结束递归
	return c[x]+Sum(x-Lowbit(x));
}

算法复杂度分析

之前也说了，查询的算法复杂度为 $O(logn)$，接下来，我来解释一下是为什么。

每次递归的时间复杂度为 $O(1)$，由于我们递归时，都是将 $x$ 一直减去 $lowbit(x)$ 到 $0$ 为止。所以递归的次数为，$x$ 在二进制表达下，数值为 $1$ 的个数。考虑最坏的情况，即 $x$ 所有二进制位都为 $1$，那时间复杂度为 $x$ 在二进制下的位数，即 $O(logn)$。

树状数组单点修改

方法

树状数组的单点修改可能比求区间和更为难懂一些，不过大家只要认真阅读，仔细思考，相信也是能快速搞定的。

设我们要将数组的第 $x$ 个数加上 $k$（如果是减去的话，就是加上 $-k$）。

我们从 $c_x$ 开始枚举所有包含 $x$ 的区间（显然，因为 $i$ 再小就不包含 $x$ 了），因为如果区间不包含 $x$ 则不会被影响，以右端点从小到大（或者说以 $c_i$ 的 $i$ 小到大，因为 $c_i$ 维护的区间的右端点为 $i$）修改每一个包含第 $x$ 个数的区间，由于所有 $c_i$ 两两枚举的区间中，要么没有公共的部分，要么一个完全包含在另一个里面，所以我们在判断是否包含时，只需看该区间的左端点是否不超过上一个被修改的 $c_i$ 的左端点，即 $c_j-lowbit(j)\le c_i-lowbit(i)$，$c_j$ 为最近一个包含 $c_i$ 的数组。

我就直接说结果了，设上一个被修改的数组下标为 $i$，那下一个被修改的数组下标就是 $i+lowbit(i)$，我们直接从 $x$ 开始一直递归或递推修改到下标超过 $n$ 为止即可。

先证明一下 $c_{i+lowbit(i)}$ 维护的区间是包含 $c_i$ 维护的区间的，即 $i+lowbit(i)-lowbit(i+lowbit(i))\le i-lowbit(i)$。设 $j$ 为 $i+lowbit(i)$，我们将问题分为两类讨论。

一种是 $lowbit(i)$ 那一位左边的一位没有 $1$。

因为 $lowbit(i)$ 那一位加了 $1$，所以肯定会发生进位，而由于左边没有紧挨着的 $1$，所以无法一直进位，所以 $lowbit(j)$ 的值为 $lowbit(i)\times 2$，而其它位不会发生变化，所以将 $j-lowbit(j)$，$i-lowbit(i)$ 减去后，剩下的位数都是相同的。即 $j-lowbit(j)=i-lowbit(i)$。

举个例子，比如 $i=18$ 时，它的二进制为 $10010$，加上 $lowbit(18)$ 为 $(10100{)}_2=20$。$20-lowbit(20)=18-lowbit(18)$，都为 $(10000{)}_2=16$。

还有一种是 $lowbit(i)$ 那一位左边的一位有 $1$。

如果 $lowbit(i)$ 左边有挨着 $1$，那 $i$ 加 $lowbit(i)$ 时，会一直进位到进的那一位为 $0$ 为止，$lowbit(j)$ 就成了 $lowbit(i)$ 左边第一个为 $0$ 的那一位。由于进位时 $lowbit(i)$ 左边紧挨着的 $1$ 都变成了 $0$，所以 $j-lowbit(j)<i-lowbit(i)$。

举个例子，比如 $i=22$ 时，它的二进制为 $10110$，加上 $lowbit(22)$ 为 $(11000{)}_2=24$。容易证明，$24-lowbit(24)<22-lowbit(22)$。

时间复杂度分析

和查询操作一样，单点修改的时间复杂度也为 $O(logn)$。接下来我解释一下是为什么。

考虑最坏的情况，即加上 $lowbit(i)$ 后只进一位，那会一直进到二进制位数大于 $n$ 为止，加 $lowbit(i)$ 的操作数为 $n$ 的二进制位数，即 $O(logn)$。

习题

P2068 统计和
P3374 【模板】树状数组 1
P3368 【模板】树状数组 2
P1908 逆序对
P1637 三元上升子序列

提示：数组数组的值不仅可以存数组的值，也可以存一个数出现的次数。如果内存不够，可以试试离散化哦。

好了，树状数组的知识点基本上就讲完了。如果对你有帮助的话，不妨就给我点一个赞吧，你们的支持是我创作的最大动力。如果该文章有表述错误或可以改进的地方，欢迎大家在评论区指出。