反向传播算法详细计算过程与结论公式

计算过程

现在我们有这样一个神经网络：

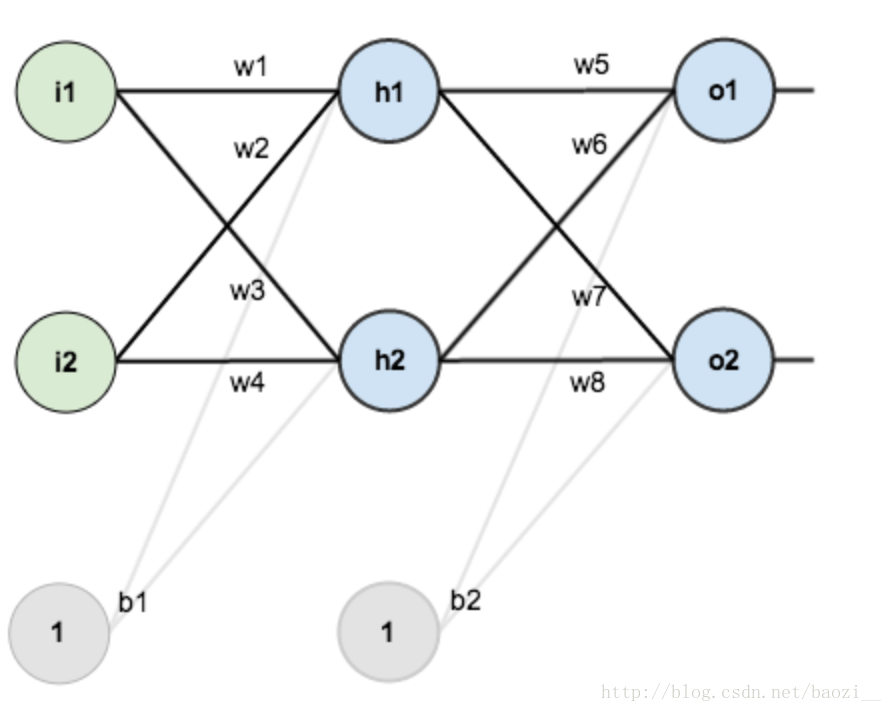
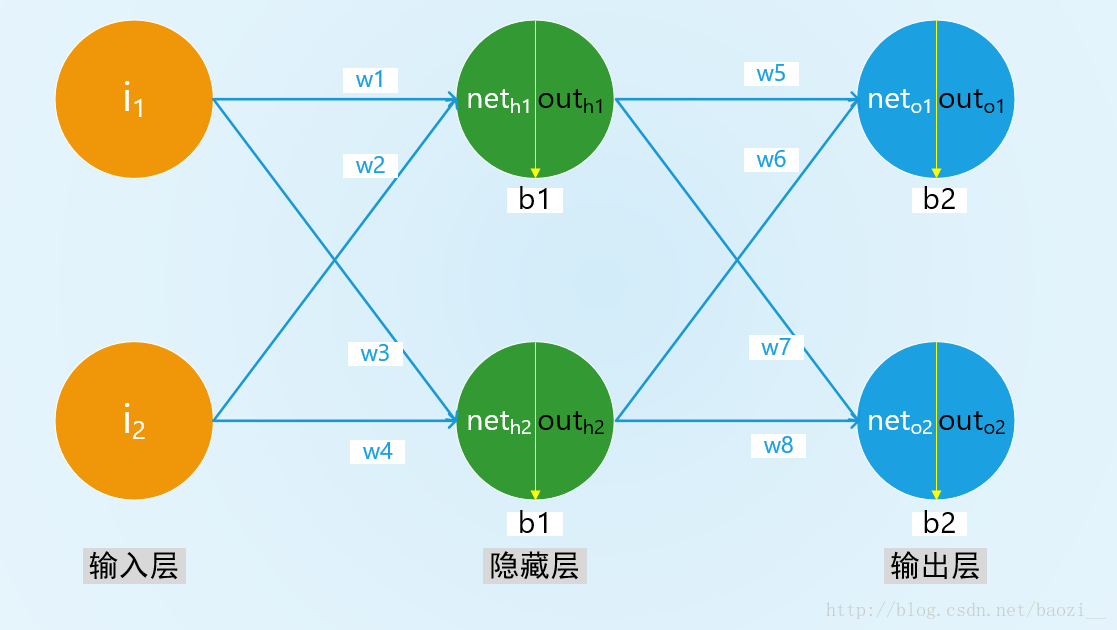
输入层有两个神经元i1和i2，隐藏层有两个神经元h1和h2，偏差都为b1，输出层有两个神经元o1和o2，偏差都为b2，权重为w
神经元的输入经过激活函数转变为输出，即带权输入net经过激活函数转变为输出激活值out，如图所示：

现在一步一步进行计算

前向传播

输入层 -> 隐藏层

计算隐藏层神经元h1与h2的带权输入：
$n e t h 1 = ω 1 * i 1 + ω 2 * i 2 + b 1$ $net_{h1}=\omega_{1}*i_{1} + \omega_{2}*i_{2}+b_{1}$
$n e t h 2 = ω 3 * i 1 + ω 4 * i 2 + b 1$ $net_{h2}=\omega_{3}*i_{1} + \omega_{4}*i_{2}+b_{1}$
计算h1与h2的输出激活值（激活函数为sigmoid函数）：

sigmoid函数： $S(x)=\frac{1}{1+e^{-x}}$

o u t h 1 = 1 1 + e - n e t h 1

$out_{h1}=\frac{1}{1+e^{-net_{h1}}}$

o u t h 2 = 1 1 + e - n e t h 2

$out_{h2}=\frac{1}{1+e^{-net_{h2}}}$

隐藏层 -> 输出层

计算输出层神经元o1与o2的带权输入：
$n e t o 1 = ω 5 * o u t h 1 + ω 6 * o u t h 2 + b 2$ $net_{o1}=\omega_{5}*out_{h1} + \omega_{6}*out_{h2}+b_{2}$
$n e t o 2 = ω 7 * o u t h 1 + ω 8 * o u t h 2 + b 2$ $net_{o2}=\omega_{7}*out_{h1} + \omega_{8}*out_{h2}+b_{2}$
计算o1与o2的输出激活值：
$o u t o 1 = 1 1 + e - n e t o 1$ $out_{o1}=\frac{1}{1+e^{-net_{o1}}}$
$o u t o 2 = 1 1 + e - n e t o 2$ $out_{o2}=\frac{1}{1+e^{-net_{o2}}}$

至此，我们就计算出了前向传播的输出，接下来进行反向传播

反向传播

计算误差（代价函数）

分别计算o1和o2的误差：

这里使用二次代价函数： $E=\frac{1}{2}(target-output)^{2}$

E o 1 = 1 2 (t a r g e t o 1 - o u t p u t o 1) 2

$E_{o1} = \frac{1}{2}(target_{o1}-output_{o1})^{2}$

E o 2 = 1 2 (t a r g e t o 2 - o u t p u t o 2) 2

$E_{o2} = \frac{1}{2}(target_{o2}-output_{o2})^{2}$ 2. 计算总误差：

总误差为： $E_{total} = \sum\frac{1}{2}(target-output)^{2}$

E t o t a l = E o 1 + E o 2

$E_{total}=E_{o1}+E_{o2}$

权值更新

微分知识告诉我们，导数体现变化率，那么权值对于总误差的影响则体现在导数上
要更新权值，就要计算总误差对权值的偏导数，即权值能对总误差产生多少影响，这里用到了链式法则

隐藏层 -> 输出层的权值更新

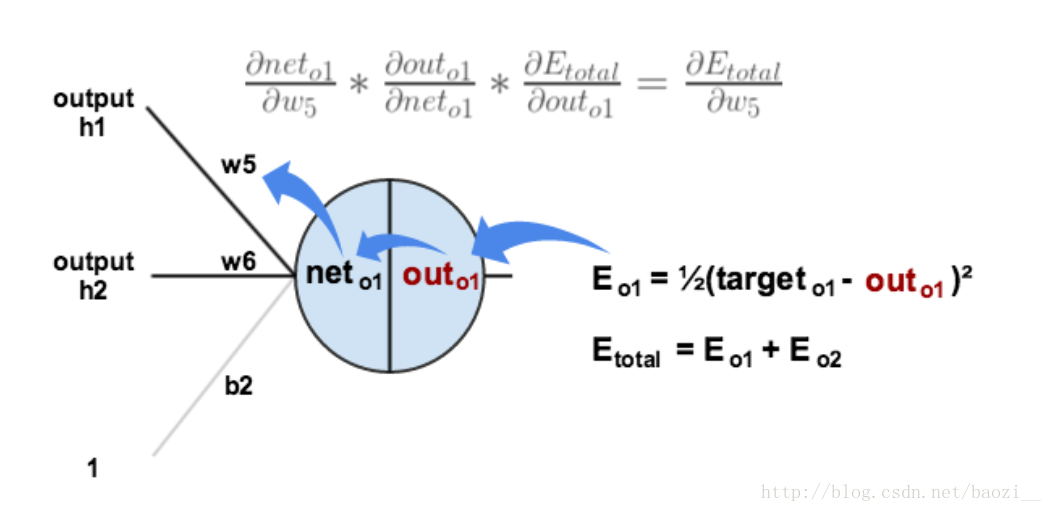
以w5为例：

$\partial E t o t a l \partial o u t o 1 * \partial o u t o 1 \partial n e t o 1 * \partial n e t o 1 \partial ω 5 = \partial E t o t a l \partial ω 5$ $\frac{\partial E_{total}}{\partial out_{o1}} * \frac{\partial out_{o1}}{\partial net_{o1}} * \frac{\partial net_{o1}}{\partial \omega_{5}} = \frac{\partial E_{total}}{\partial \omega_{5}}$
下图可以更直观的感受反向传播误差：
分别计算等号左边的三个式子：
- $\frac{\partial E_{total}}{\partial out_{o1}}$ ：
  $E t o t a l = 1 2 (t a r g e t o 1 - o u t p u t o 1) 2 + 1 2 (t a r g e t o 2 - o u t p u t o 2) 2$ $E_{total} = \frac{1}{2}(target_{o1}-output_{o1})^{2} + \frac{1}{2}(target_{o2}-output_{o2})^{2}$
  $\partial E t o t a l \partial o u t o 1 = - (t a r g e t o 1 - o u t p u t o 1)$ $\frac{\partial E_{total}}{\partial out_{o1}} = -(target_{o1} - output_{o1})$
- $\frac{\partial out_{o1}}{\partial net_{o1}}$ (即对sigmoid函数求导):
  $o u t o 1 = 1 1 + e - n e t o 1$ $out_{o1}=\frac{1}{1+e^{-net_{o1}}}$
  $\partial o u t o 1 \partial n e t o 1 = o u t o 1 (1 - o u t o 1)$ $\frac{\partial out_{o1}}{\partial net_{o1}} = out_{o1}(1 - out_{o1})$
- $\frac{\partial net_{o1}}{\partial \omega_{5}}$ ：
  $n e t o 1 = ω 5 * o u t h 1 + ω 6 * o u t h 2 + b 2$ $net_{o1}=\omega_{5} * out_{h1}+\omega_{6} * out_{h2}+b_{2}$
  $\partial n e t o 1 \partial ω 5 = o u t h 1$ $\frac{\partial net_{o1}}{\partial \omega_{5}} = out_{h1}$
然后乘起来即可：

$\partial E t o t a l \partial ω 5 = - (t a r g e t o 1 - o u t p u t o 1) * o u t o 1 (1 - o u t o 1) * o u t h 1$ $\frac{\partial E_{total}}{\partial \omega_{5}} = -(target_{o1} - output_{o1}) * out_{o1}(1 - out_{o1}) * out_{h1}$
现在我们得到了整体误差E(total)对w5的偏导值，为了表达方便，在此我们定义：

$\delta$ 为神经元的误差
（与上文提到的误差不同，上文着重最终结果的误差，此处更着重单个神经元的误差）
那么δo1即为神经元o1的误差，即：

$δ o 1 = \partial E t o t a l \partial o u t o 1 * \partial o u t o 1 \partial n e t o 1 = \partial E t o t a l \partial n e t o 1$ $\delta_{o1} = \frac{\partial E_{total}}{\partial out_{o1}} * \frac{\partial out_{o1}}{\partial net_{o1}} = \frac{\partial E_{total}}{\partial net_{o1}}$
$δ o 1 = - (t a r g e t o 1 - o u t p u t o 1) * o u t o 1 (1 - o u t o 1)$ $\delta_{o1} = -(target_{o1} - output_{o1}) * out_{o1}(1 - out_{o1})$
所以，整体误差E(total)对w5的偏导为：
$\partial E t o t a l \partial ω 5 = δ o 1 * o u t h 1$ $\frac{\partial E_{total}}{\partial \omega_{5}} = \delta_{o1} * out_{h1}$
最后，w5得到更新：
$ω 5 \to ω 5 - η * \partial E t o t a l \partial ω 5$ $\omega_{5} \rightarrow \omega_{5} - \eta * \frac{\partial E_{total}}{\partial \omega_{5}}$

$\eta$ 是学习速率，也叫步长

输入层（隐藏层） -> 隐藏层的权值更新

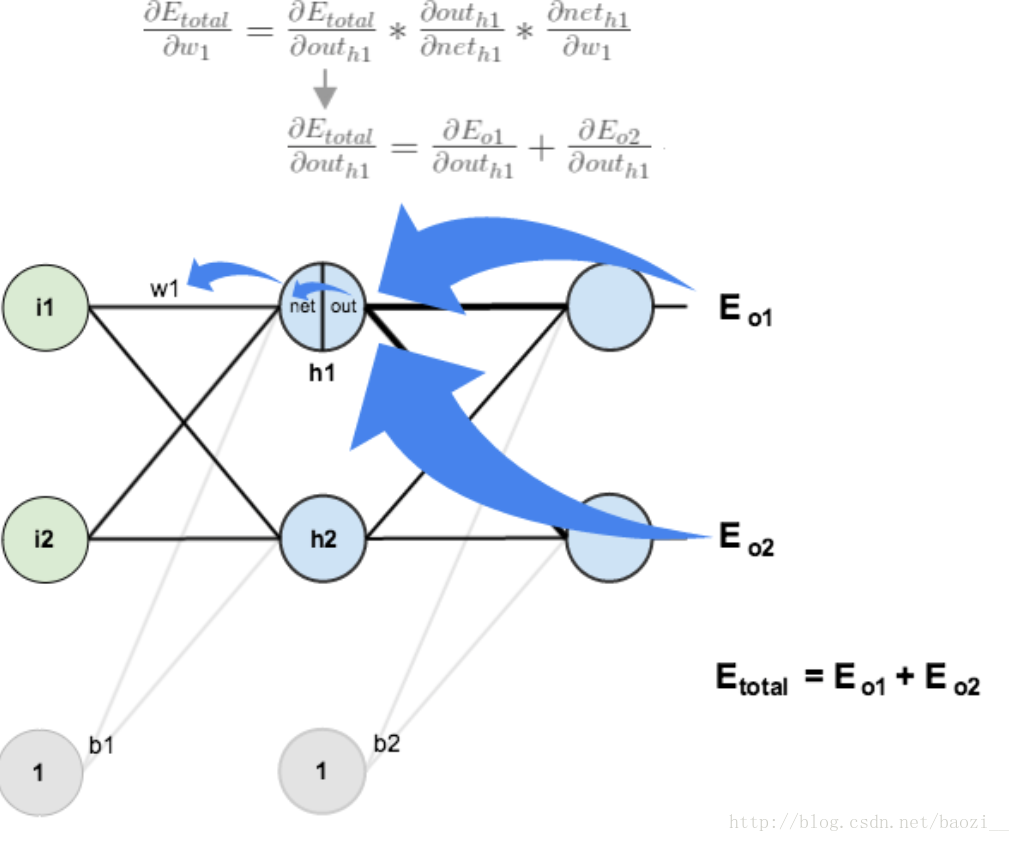
以w1为例：

$\partial E t o t a l \partial o u t h 1 * \partial o u t h 1 \partial n e t h 1 * \partial n e t h 1 \partial ω 1 = \partial E t o t a l \partial ω 1$ $\frac{\partial E_{total}}{\partial out_{h1}} * \frac{\partial out_{h1}}{\partial net_{h1}} * \frac{\partial net_{h1}}{\partial \omega_{1}} = \frac{\partial E_{total}}{\partial \omega_{1}}$
计算方法与上面类似，但是有个地方需要变一下，在计算h1的误差时，out(h1)会接受来自o1和o2两个神经元的误差，所以在这两个都要计算
分别计算等号左边的三个式子：
- $\frac{\partial E_{total}}{\partial out_{h1}}$ ：
  $\partial E t o t a l \partial o u t h 1 = \partial E o 1 \partial o u t h 1 + \partial E o 2 \partial o u t h 1$ $\frac{\partial E_{total}}{\partial out_{h1}} = \frac{\partial E_{o1}}{\partial out_{h1}} + \frac{\partial E_{o2}}{\partial out_{h1}}$
  先计算 $\frac{\partial E_{o1}}{\partial out_{h1}}$ ：
  $\partial E o 1 \partial o u t h 1 = \partial E o 1 \partial n e t o 1 * \partial n e t o 1 \partial o u t h 1$ $\frac{\partial E_{o1}}{\partial out_{h1}} = \frac{\partial E_{o1}}{\partial net_{o1}} * \frac{\partial net_{o1}}{\partial out_{h1}}$
  其中：
  $\partial E o 1 \partial n e t o 1 = \partial E o 1 \partial o u t o 1 * \partial o u t o 1 \partial n e t o 1$ $\frac{\partial E_{o1}}{\partial net_{o1}} = \frac{\partial E_{o1}}{\partial out_{o1}} * \frac{\partial out_{o1}}{\partial net_{o1}}$
  $n e t o 1 = ω 5 * o u t h 1 + ω 6 * o u t h 2 + b 2$ $net_{o1} = \omega_{5}*out_{h1} + \omega_{6}*out_{h2}+b_{2}$
  $\partial n e t o 1 \partial o u t h 1 = ω 5$ $\frac{\partial net_{o1}}{\partial out_{h1}} = \omega_{5}$
  得到：
  $\partial E o 1 \partial o u t h 1 = \partial E o 1 \partial o u t o 1 * \partial o u t o 1 \partial n e t o 1 * ω 5$ $\frac{\partial E_{o1}}{\partial out_{h1}} = \frac{\partial E_{o1}}{\partial out_{o1}} * \frac{\partial out_{o1}}{\partial net_{o1}} * \omega_{5}$
  代入上边计算出的结果可得：
  $\partial E o 1 \partial o u t h 1 = - (t a r g e t o 1 - o u t p u t o 1) * o u t o 1 (1 - o u t o 1) * ω 5$ $\frac{\partial E_{o1}}{\partial out_{h1}} = -(target_{o1} - output_{o1}) * out_{o1}(1 - out_{o1}) * \omega_{5}$
  观察1，2两个式子，我们可以发现，等号右边的左边两项，其实就是δo1，所以上式可以化简为：
  $\partial E o 1 \partial o u t h 1 = δ o 1 * ω 5$ $\frac{\partial E_{o1}}{\partial out_{h1}} = \delta_{o1} * \omega_{5}$
  同理可得另一项：
  $\partial E o 2 \partial o u t h 1 = δ o 2 * ω 7$ $\frac{\partial E_{o2}}{\partial out_{h1}} = \delta_{o2} * \omega_{7}$
  然后加起来便得到第一项：
  $\partial E t o t a l \partial o u t h 1 = δ o 1 * ω 5 + δ o 2 * ω 7$ $\frac{\partial E_{total}}{\partial out_{h1}} = \delta_{o1} * \omega_{5} + \delta_{o2} * \omega_{7}$
- $\frac{\partial out_{h1}}{\partial net_{h1}}$ (即对sigmoid函数求导):
  $o u t h 1 = 1 1 + e - n e t h 1$ $out_{h1}=\frac{1}{1+e^{-net_{h1}}}$
  $\partial o u t h 1 \partial n e t h 1 = o u t h 1 (1 - o u t h 1)$ $\frac{\partial out_{h1}}{\partial net_{h1}} = out_{h1}(1 - out_{h1})$
- $\frac{\partial net_{h1}}{\partial \omega_{1}}$ ：
  $n e t h 1 = ω 1 * i 1 + ω 2 * i 2 + b 1$ $net_{h1}= \omega_{1}*i_{1} + \omega_{2}*i_{2}+b_{1}$
  $\partial n e t h 1 \partial ω 1 = i 1$ $\frac{\partial net_{h1}}{\partial \omega_{1}} = i_{1}$
然后乘起来即可：

$\partial E t o t a l \partial ω 1 = (δ o 1 * ω 5 + δ o 2 * ω 7) * o u t h 1 (1 - o u t h 1) * i 1$ $\frac{\partial E_{total}}{\partial \omega_{1}} = (\delta_{o1} * \omega_{5} + \delta_{o2} * \omega_{7}) * out_{h1}(1 - out_{h1}) * i_{1}$
那么δh1即为神经元h1的误差，即：
$δ h 1 = \partial E t o t a l \partial o u t h 1 * \partial o u t h 1 \partial n e t h 1 = \partial E t o t a l \partial n e t h 1$ $\delta_{h1} = \frac{\partial E_{total}}{\partial out_{h1}} * \frac{\partial out_{h1}}{\partial net_{h1}} = \frac{\partial E_{total}}{\partial net_{h1}}$
$δ h 1 = (δ o 1 * ω 5 + δ o 2 * ω 7) * o u t h 1 (1 - o u t h 1)$ $\delta_{h1} = (\delta_{o1} * \omega_{5} + \delta_{o2} * \omega_{7}) * out_{h1}(1 - out_{h1})$
所以，整体误差E(total)对w1的偏导为：
$\partial E t o t a l \partial ω 1 = δ h 1 * i 1$ $\frac{\partial E_{total}}{\partial \omega_{1}} = \delta_{h1} * i_{1}$
最后，w5得到更新：
$ω 1 \to ω 1 - η * \partial E t o t a l \partial ω 1$ $\omega_{1} \rightarrow \omega_{1} - \eta * \frac{\partial E_{total}}{\partial \omega_{1}}$

结论公式

首先我们重新规定一下命名，z表示带权输入，a表示输出激活值，即为经过激活函数的带权输入，C表示代价函数，L表示神经网络的层数。

现在我们以sigmoid激活函数为例，用四个公式总结一下反向传播算法：

输出层误差的方程

L层第j个神经元的误差：

δ L j = \partial C \partial a L j * σ' (z L j)

$\delta^{L}_{j} = \frac{\partial C}{\partial a^{L}_{j}} * \sigma'(z^{L}_{j})$
用微分算子表示的矩阵形式为：

δ L = \nabla a C ⊙ σ' (z L)

$\delta^{L} = \nabla_{a}C \odot \sigma'(z^{L})$

使用下一层的误差表示当前层的误差

下一层的误差呈上下一层的权重值，再点乘上当前层的输出，即为当前层的误差：

δ l = (δ l + 1 (ω l + 1) T) ⊙ σ' (z l)

$\delta^{l} = (\delta^{l+1}(\omega^{l+1})^{T}) \odot \sigma'(z^{l})$

偏置b在代价函数C中的改变率

仔细观察上述计算过程可以发现，偏置b是带权输入z中的一项，而且偏置b的系数为1，所以我们可以得出，代价函数C对某神经元的偏置b的偏导即为该神经元的误差：

\partial C \partial b = δ

$\frac{\partial C}{\partial b} = \delta$

权重ω在代价函数C中的改变率

根据带权输入的表达式(ain为输入该神经元的激活值)：

z = ω * a i n + b

$z = ω * a_{in} + b$
可知，代价函数 C对 ω的偏导是在误差的基础上乘上了输入激活值：

\partial C \partial ω = a i n * δ o u t

$\frac{\partial C}{\partial \omega} = a_{in} * \delta_{out}$

总结

四个公式：

δ L = \nabla a C ⊙ σ' (z L)

$\delta^{L} = \nabla_{a}C \odot \sigma'(z^{L})$

δ l = (δ l + 1 (ω l + 1) T) ⊙ σ' (z l)

$\delta^{l} = (\delta^{l+1}(\omega^{l+1})^{T}) \odot \sigma'(z^{l})$

\partial C \partial b = δ

$\frac{\partial C}{\partial b} = \delta$

\partial C \partial ω = a i n * δ o u t

$\frac{\partial C}{\partial \omega} = a_{in} * \delta_{out}$

参考：
1. http://www.cnblogs.com/charlotte77/p/5629865.html
2. http://neuralnetworksanddeeplearning.com/