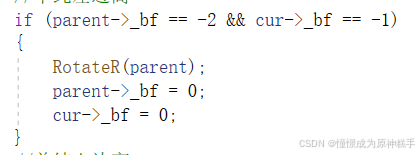目录
3.2 更新后parent的平衡因子等于1 或 -1,需要继续往上更新。
3.3 更新后parent的平衡因子等于2 或 -2,需要使用旋转处理。
一. AVL的概念
1.AVL树是最先发明的自平衡二叉查找树,AVL是一颗空树,或者具备下列性质的二叉搜索树:它的
左右子树都是AV树,且 左右子树的高度差的绝对值不超过1 。AVL树是一颗高度平衡搜索二叉树,通过控制高度差去控制平衡!!!
2.AVL树实现这里我们引入一个平衡因子(balance factor)的概念,每个结点都有一个平衡因子,任何结点的平衡因子等于右子树的高度减去左子树的高度,也就是说任何结点的平衡因子等于0/1/-1
AVL树并不是必须要平衡因子,但是有了平衡因子可以更方便我们去进行观察和控制树是否平衡
就像一个风向标一样。
二 AVL树的插入
AVL节点 的大概结构 AVL树 的大概结构

2.1先按二叉搜索树的规则插入
具体可以看这篇
这里是二叉搜索树的,简单的代码总结
2.2 AVL的重点:平衡因子更新
因为:左右子树的高度差的绝对值不超过1 。
这里我们可以规定
1. 平衡因子 = 右子树高度 - 左子树高度 。
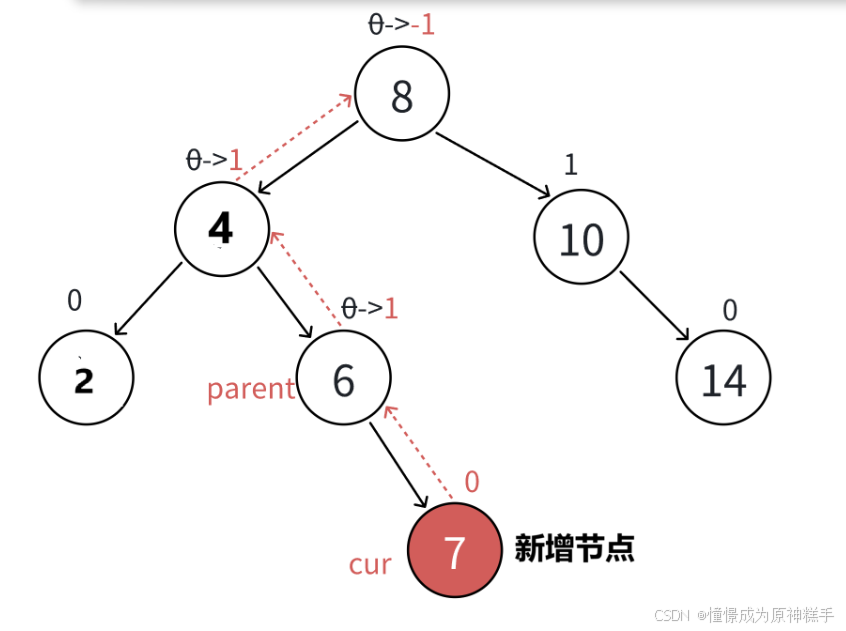
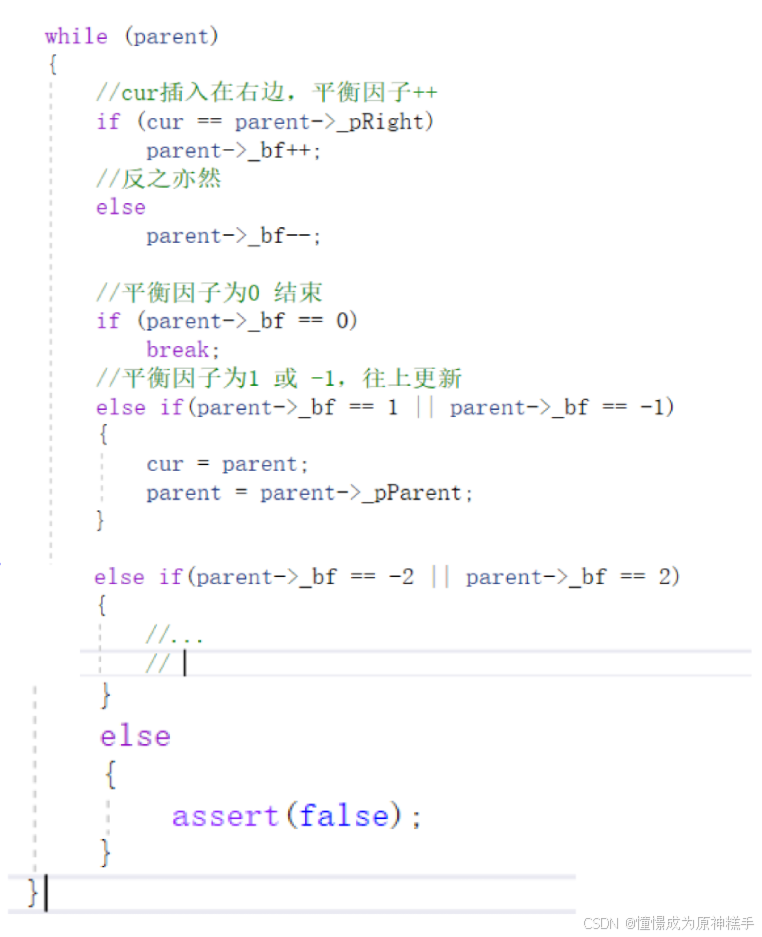
2. 插入结点时,会增加高度,如果新增结点 在parent的右子树,parent的平衡因子++,新增结点在parent的左子树,parent平衡因子--,parent的平衡因子初始化为 0.
3. parent的停止更新条件分为3种:
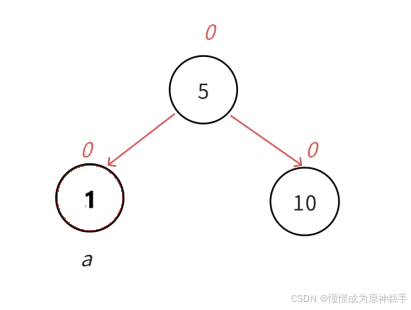
3.1 更新后parent的平衡因子等于0。
3.2 更新后parent的平衡因子等于1 或 -1,需要继续往上更新。
上面的总代码:
3.3 更新后parent的平衡因子等于2 或 -2,需要使用旋转处理。
下面为具体的分析:
三.旋转 和 平衡因子等于2 或 -2 的处理
旋转总共分为四种,左单旋/右单旋/左右双旋/右左双旋。
这里我们规定:
1. 在parent的左边 插入孩子,parent的平衡因子 - 1
2 .在parent的右边 插入孩子,parent的平衡因子 + 1
1.右单旋(把左孩子变成爸爸)
需要 单纯的左边高!!! 才可以使用
比如 if(parent->_bf == -2 && SubR->_bf == -1)
如图:
分析:
因为 左右子树的高度差的绝对值不超过1
我们需要把 a 往上提,把parent往下压 ,让SubL变成爸爸 才可以解决。
总的来说就是,左边高就把左边提上来,把右边压下去。
在这种情况下 他们的平衡因子就会为0.
代码为:
RotateR:
2.左单旋(把右孩子变成爸爸)
需要 单纯的右边高!!! 才可以使用
比如 if(parent->_bf == 2 && SubR->_bf == 1)
如图:
分析:
因为 左右子树的高度差的绝对值不超过1
我们需要把 a 往上提,把parent往下压 ,让SubR变成爸爸 才可以解决。
总的来说就是,右边高就把右边提上来,把左边压下去。
在这种情况下 他们的平衡因子就会为0.
代码为:
RotateL:
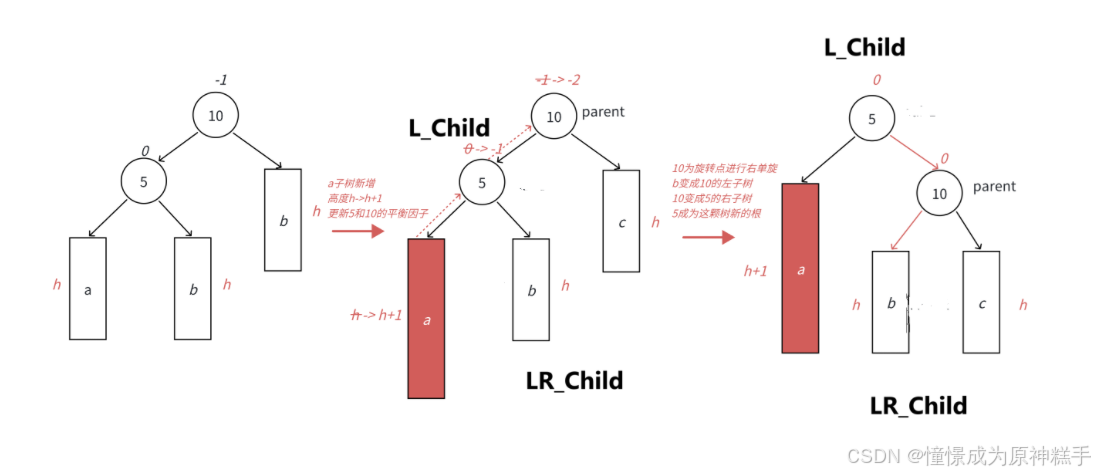
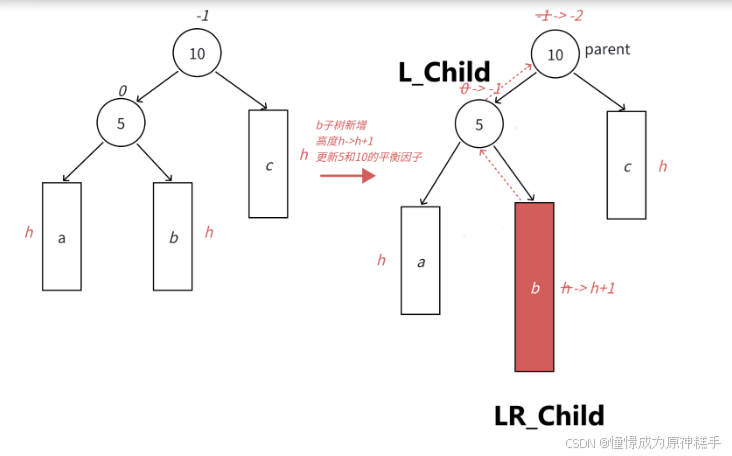
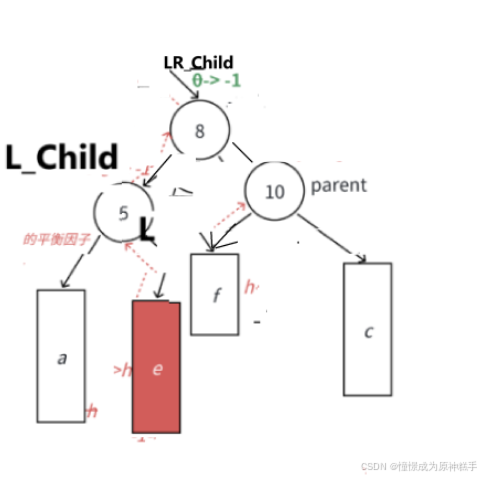
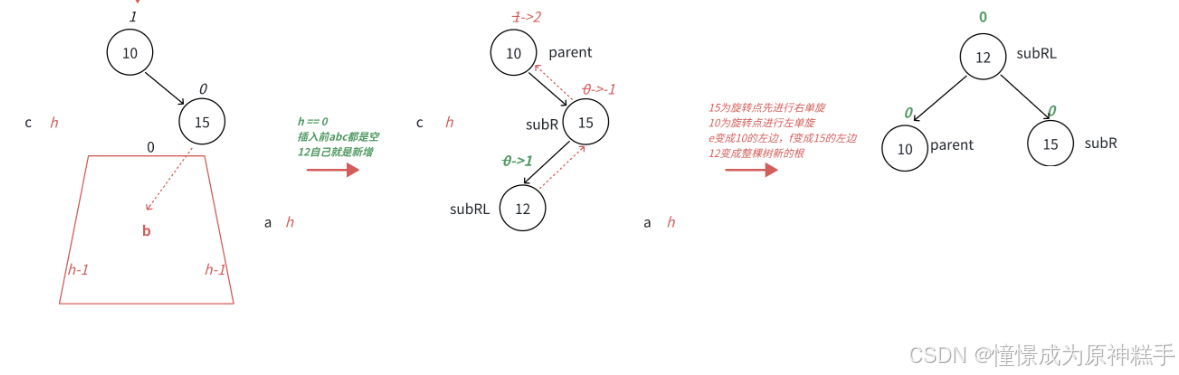
3.左右双旋(把LR_Child 变为爸爸)
需要 左边的右边高!!! 才可以使用
如图所示:
当没插入节点时:
在LR_Child 的左边插入节点:
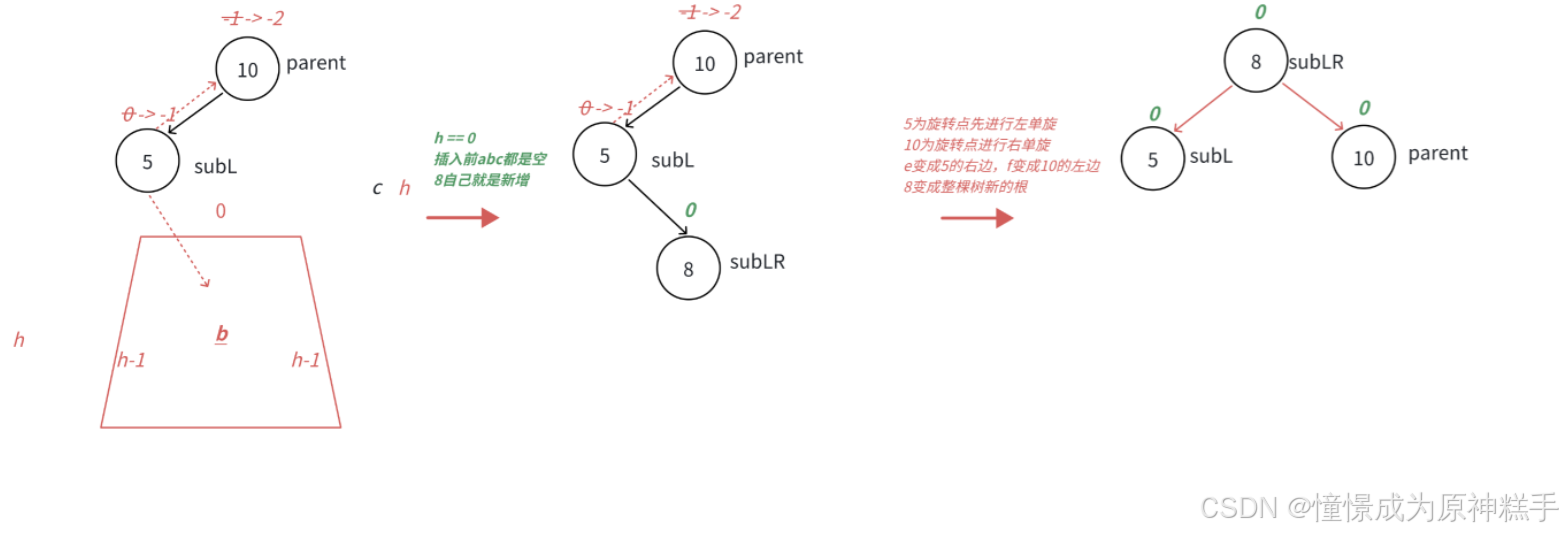
具体过程
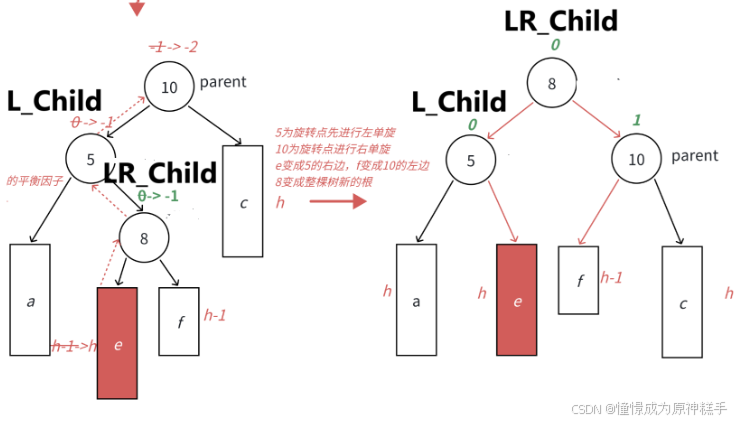
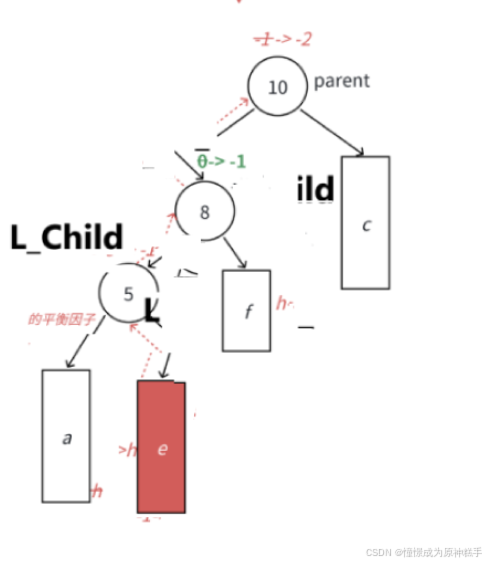
1. 让节点5 左旋转:
2.让节点8 右旋转
平衡因子:
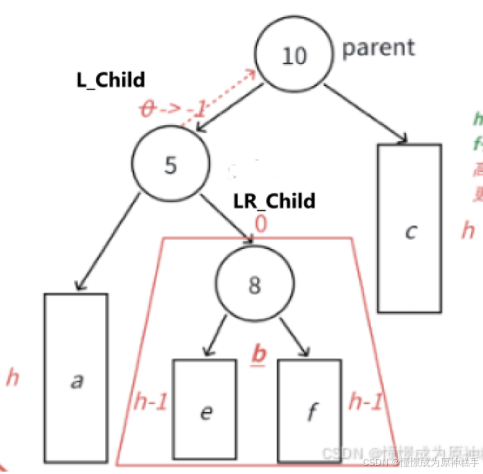
在LR_Child 为空时
平衡因子 都为0.
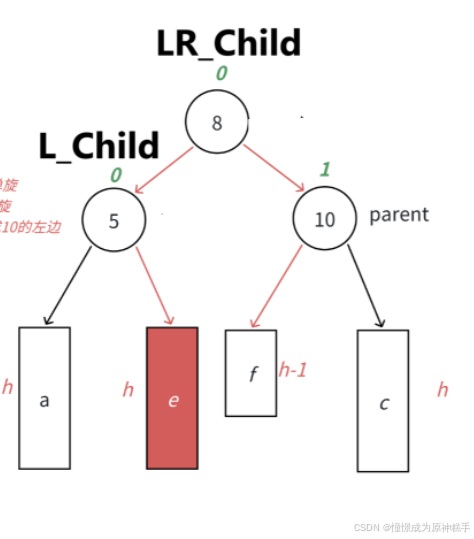
在LR_Child 的左边插入节点:
LR_Child 平衡因子 为 0
L_Child 平衡因子 为 0
parent 平衡因子为 1
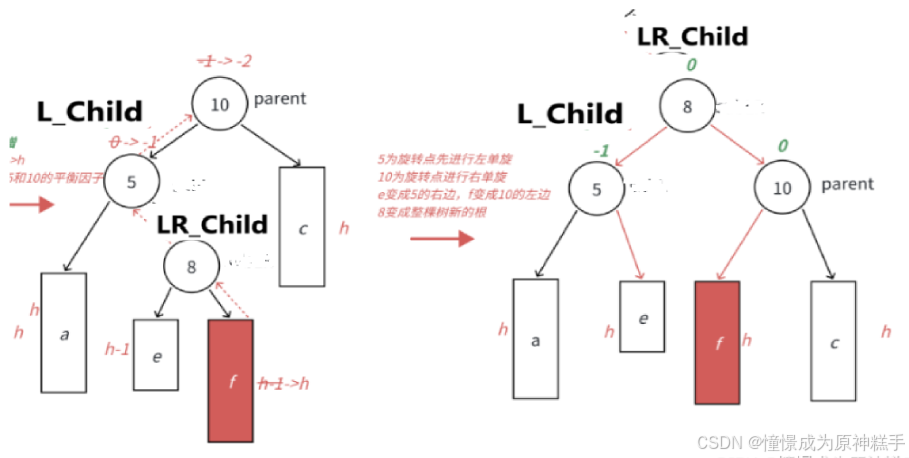
在LR_Child 的右边插入节点:
LR_Child 平衡因子 为 0
L_Child 平衡因子 为 -1
parent 平衡因子为 0
代码:
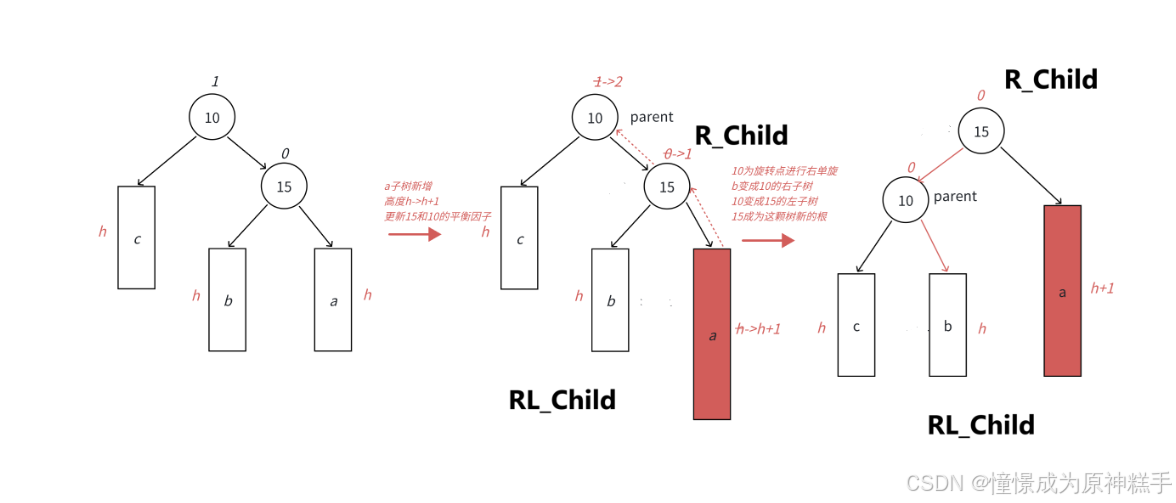
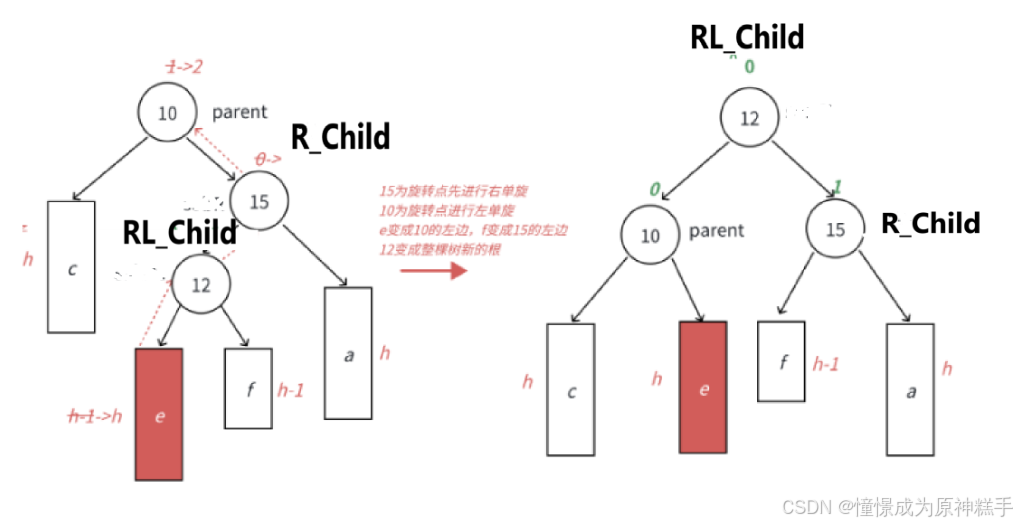
4.左右双旋(把RL_Child 变为爸爸)
太长了,随便写点了,脑子坏了!!!
在LR_Child 为空时
平衡因子 都为0.
在LR_Child 的右边插入节点:
RL_Child 平衡因子 为 0
R_Child 平衡因子 为 0
parent 平衡因子为 -1
在RL_Child 的左边插入节点:
RL_Child 平衡因子 为 0
R_Child 平衡因子 为 1
parent 平衡因子为 0
代码:
总代码:
#pragma once
#include<iostream>
#include<assert.h>
using namespace std;
template<class T>
struct AVLTreeNode
{
AVLTreeNode(const T& data = T())
: _pLeft(nullptr)
, _pRight(nullptr)
, _pParent(nullptr)
, _data(data)
, _bf(0)
{}
AVLTreeNode<T>* _pLeft;
AVLTreeNode<T>* _pRight;
AVLTreeNode<T>* _pParent;
T _data;
int _bf; // 节点的平衡因子
};
// AVL: 二叉搜索树 + 平衡因子的限制
template<class T>
class AVLTree
{
typedef AVLTreeNode<T> Node;
public:
AVLTree()
: _pRoot(nullptr)
{}
// 在AVL树中插入值为data的节点
bool Insert(const T& data)
{
//如果树为空就建立一个根节点
if (_pRoot == nullptr)
{
_pRoot = new Node(data);
}
//树不为空
else
{
Node* parent = nullptr;
Node* tmp = _pRoot;
//用cur找位置
while (tmp)
{
//插入值比当前结点小往左走
if (tmp->_data < data)
{
parent = tmp;
tmp = tmp->_pRight;
}
//插入值比当前结点大往右走
else if (tmp->_data > data)
{
parent = tmp;
tmp = tmp->_pLeft;
}
else
{
assert(false);
}
}
//在parent的左边或者右边插入插入
Node* cur = new Node(data);
if (parent->_data < data)
{
parent->_pRight = cur;
cur->_pParent = parent;
}
else if (parent->_data > data)
{
parent->_pLeft = cur;
cur->_pParent = parent;
}
//最困难的平衡因子部分
while (parent)
{
//cur插入在右边,平衡因子++
if (cur == parent->_pRight)
parent->_bf++;
//反之亦然
else
parent->_bf--;
//平衡因子为0 结束
if (parent->_bf == 0)
break;
//平衡因子为1 或 -1,往上更新
else if(parent->_bf == 1 || parent->_bf == -1)
{
cur = parent;
parent = parent->_pParent;
}
else if(parent->_bf == -2 || parent->_bf == 2)
{
//...
//
//单纯左边高
if (parent->_bf == -2 && cur->_bf == -1)
{
RotateR(parent);
parent->_bf = 0;
cur->_bf = 0;
}
//单纯右边高
else if (parent->_bf == 2 && cur->_bf == 1)
{
RotateL(parent);
parent->_bf = 0;
cur->_bf = 0;
}
//左边的右边高
else if (parent->_bf == -2 && cur->_bf == 1)
{
RotateLR(parent);
}
//右边的左边高
else if (parent->_bf == 2 && cur->_bf == -1)
{
RotateRL(parent);
}
else
{
assert(false);
}
break;
}
else
{
assert(false);
}
}
}
return true;
}
// AVL树的验证
bool IsAVLTree()
{
return _Height(_pRoot);
}
void InOrder()
{
return _InOrder(_pRoot);
}
size_t Height()
{
return _Height(_pRoot);
}
private:
// 根据AVL树的概念验证pRoot是否为有效的AVL树
bool _IsAVLTree(Node* pRoot)
{
if (pRoot == nullptr)
return true;
int left = _Height(pRoot->_pLeft);
int right = _Height(pRoot->_pRight);
int differ = right - left;
if (differ >= 2 || differ <= -2)
return false;
if (differ != pRoot->_bf)
return false;
return _IsAVLTree(pRoot->_pLeft) && _IsAVLTree(pRoot->_pRight);
}
void _InOrder(Node* cur)
{
if (cur == nullptr)
return;
_InOrder(cur->_pLeft);
cout << cur->_data << " ";
_InOrder(cur->_pRight);
}
size_t _Height(Node* pRoot)
{
if (pRoot == nullptr)
return 0;
size_t left = _Height(pRoot->_pLeft);
size_t right = _Height(pRoot->_pRight);
return right > left ? right + 1 : left + 1;
}
// 右单旋
void RotateR(Node* pParent)
{
Node* L_Child = pParent->_pLeft;
Node* LR_Child = L_Child->_pRight;
//左边孩子的 右边的孩子 和parent相互连接
if (LR_Child)
LR_Child->_pParent = pParent;
pParent->_pLeft = LR_Child;
//左孩子变在上面 右边连接parent ,grandfather 相互连接
Node* grandfather = pParent->_pParent;
pParent->_pParent = L_Child;
L_Child->_pRight = pParent;
L_Child->_pParent = grandfather;
if (grandfather == nullptr)
{
_pRoot = L_Child;
}
else
{
if (grandfather->_pLeft == pParent)
grandfather->_pLeft = L_Child;
else
grandfather->_pRight = L_Child;
}
}
// 左单旋
void RotateL(Node* pParent)
{
Node* R_Child = pParent->_pRight;
Node* RL_Child = R_Child->_pLeft;
//
if(RL_Child)
RL_Child->_pParent = pParent;
pParent->_pRight = RL_Child;
Node* grandfather = pParent->_pParent;
pParent->_pParent = R_Child;
R_Child->_pLeft = pParent;
R_Child->_pParent = grandfather;
if (grandfather == nullptr)
{
_pRoot = R_Child;
}
else
{
if (grandfather->_pLeft == pParent)
grandfather->_pLeft = R_Child;
else
grandfather->_pRight = R_Child;
}
}
// 右左双旋
void RotateRL(Node* pParent)
{
Node* RChild = pParent->_pRight;
Node* RLChild = RChild->_pLeft;
//旋转完之后再用bf来判断平衡因子
int bf = RLChild->_bf;
RotateR(RChild);
RotateL(pParent);
if (bf == 0)
{
pParent->_bf = 0;
RChild->_bf = 0;
RLChild->_bf = 0;
}
else if (bf == 1)
{
RLChild->_bf = 0;
RChild->_bf = 0;
pParent->_bf = -1;
}
else if (bf == -1)
{
RLChild->_bf = 0;
RChild->_bf = 1;
pParent->_bf = 0;
}
else
assert(false);
}
// 左右双旋
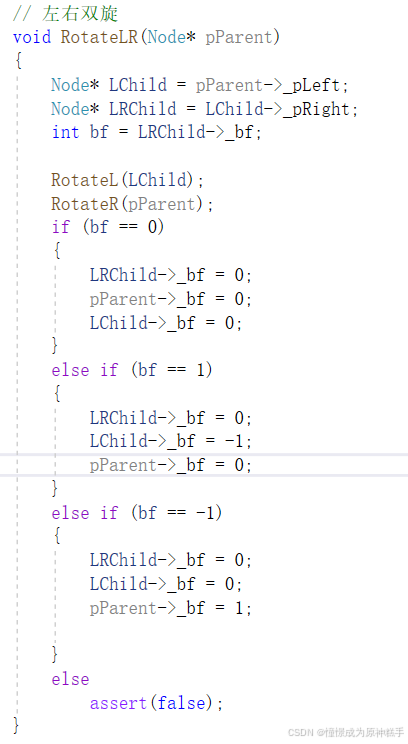
void RotateLR(Node* pParent)
{
Node* LChild = pParent->_pLeft;
Node* LRChild = LChild->_pRight;
int bf = LRChild->_bf;
RotateL(LChild);
RotateR(pParent);
if (bf == 0)
{
LRChild->_bf = 0;
pParent->_bf = 0;
LChild->_bf = 0;
}
else if (bf == 1)
{
LRChild->_bf = 0;
LChild->_bf = -1;
pParent->_bf = 0;
}
else if (bf == -1)
{
LRChild->_bf = 0;
LChild->_bf = 0;
pParent->_bf = 1;
}
else
assert(false);
}
private:
Node* _pRoot;
};