35. 图像物体的边界

题目描述

给定一个二维数组M行N列，二维数组里的数字代表图片的像素，为了简化问题，仅包含像素1和5两种像素，每种像素代表一个物体，2个物体相邻的格子为边界，求像素1代表的物体的边界个数。
像素1代表的物体的边界指与像素5相邻的像素1的格子，边界相邻的属于同一个边界，相邻需要考虑8个方向（上，下，左，右，左上，左下，右上，右下）。
其他约束：
地图规格约束为：
0<M<100
0<N<100
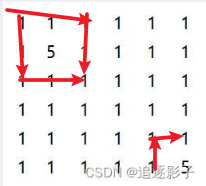
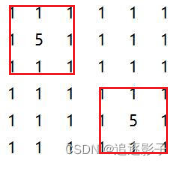
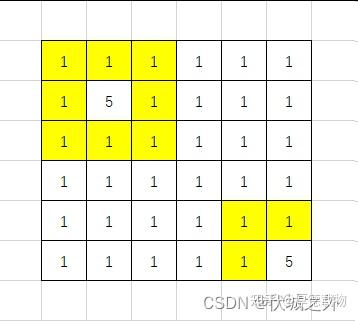
1）如下图，与像素5的格子相邻的像素1的格子（0,0）、（0,1）、（0,2）、（1,0）、（1,2）、（2,0）、（2,1）、（2,2）、（4,4）、（4,5）、（5,4）为边界，另（0,0）、（0,1）、（0,2）、（1,0）、（1,2）、（2,0）、（2,1）、（2,2）相邻，为1个边界，（4,4）、（4,5）、（5,4）相邻，为1个边界，所以下图边界个数为2。

6 6

1 1 1 1 1 1

1 5 1 1 1 1

1 1 1 1 1 1

1 1 1 1 1 1

1 1 1 1 1 1

1 1 1 1 1 5
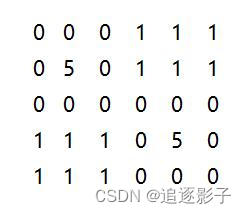
2）如下图，与像素5的格子相邻的像素1的格子（0,0）、（0,1）、（0,2）、（1,0）、（1,2）、（2,0）、（2,1）、（2,2）、（3,3）、（3,4）、（3,5）、（4,3）、（4,5）、（5,3）、（5,4）、（5,5）为边界，另这些边界相邻，所以下图边界个数为1。注：（2,2）、（3,3）相邻。

6 6

1 1 1 1 1 1

1 5 1 1 1 1

1 1 1 1 1 1

1 1 1 1 1 1

1 1 1 1 5 1

1 1 1 1 1 1

输入描述:

第一行，行数M，列数N 第二行开始，是M行N列的像素的二维数组，仅包含像素1和5

输出描述:

像素1代表的物体的边界个数。如果没有边界输出0（比如只存在像素1，或者只存在像素5）。

思路

一、问题分析

首先读题，仔细看描述中的内容，发现需求是

1.给定一个二维数组M行N列，

2.二维数组里的数字代表图片的像素，

3.为了简化问题，仅包含像素1和5两种像素

4.每种像素代表一个物体，

5.2个物体相邻的格子为边界，

6.求像素1代表的物体的边界个数。

7.像素1代表的物体的边界指与像素5相邻的像素1的格子，

8.边界相邻的属于同一个边界，

9.相邻需要考虑8个方向（上，下，左，右，左上，左下，右上，，右下）。

10.其他约束：地图规格约束为：M、N均大于0小于100

11.输入描述：第一行，行数M，列数N

第二行开始，是M行N列的像素的二维数组，仅包含像素1和5

12.输出描述：像素1代表的物体的边界个数。如果没有边界输出0（比如只存在像素1，或者只存在像素5）。

二、解题思路

1.首先我们需要定义两个整数M和N用于存储行数和列数

int M, N;

scanf("%d %d", &M, &N);

2.定义一个int arr5[M * N][3];用来储存像素5格子的坐标，以及是否被访问过

3.然后我们读取像素为5的格子的坐标，

4.遍历像素为5的格子的坐标，对于每个格子，我们如果之前没有访问过，我们bnumber（边界数量）加一，然后检查所有这个格子后面的格子在这个格子的x，y坐标+-3范围内是否有其他像素为5的格子，如果有我们标记成已访问（因为属于同一边界）。

5.对于已经访问过的格子我们不做重复的搜索。

三、具体步骤

使用的语言是C

#include <stdio.h>
#include <stdbool.h>

void findHelper(int arr5[][3], int idx5, int current) {
    for(int i = current + 1; i < idx5; i++) {
        if((arr5[i][0] >= arr5[current][0] - 3) && (arr5[i][0] <= arr5[current][0] + 3) && (arr5[i][1] >= arr5[current][1] - 3) && (arr5[i][1] <= arr5[current][1] + 3)) {
            arr5[i][2] = 1;
        }
    }
}

int findBoundary(int arr5[][3], int idx5) {
    int bnumber = 0;
    for (int i = 0; i < idx5; i++) {
        if(arr5[i][2] == 1) continue;
        else if(arr5[i][2] == 0) {
            arr5[i][2] = 1;
            bnumber++;
            // printf("at position x:%d, y:%d\n", arr5[i][0], arr5[i][1]);
            findHelper(arr5, idx5, i);
        }
    }
    return bnumber;
}

int main() {
    int M, N;
    scanf("%d %d", &M, &N);
    printf("The M is %d, N is %d\n", M, N);
    if (M == 0 || N == 0) {
        printf("0\n");
        return 0;
    }
    int arr5[M * N][3];
    int idx5 = 0;
    bool have1 = false;
    int tempnum;
    for (int i = 0; i < M; i++) {
        for (int j = 0; j < N; j++) {
            scanf("%d", &tempnum);
            if (tempnum == 5) {
                arr5[idx5][0] = i;
                arr5[idx5][1] = j;
                arr5[idx5][2] = 0;
                idx5++;
            }
            if (tempnum == 1) {
                have1 = true;
            }
        }
    }
    if (idx5 > 0 && have1) {
        int anwser = findBoundary(arr5, idx5);
        printf("%d\n", anwser);
    } else {
        printf("0\n");
    }
    return 0;
}