通过一段时间的学习,总算把逻辑回归模型弄清楚了
《老饼讲解-机器学习》www.bbbdata.com中是讲得最清晰的,结合其它资料,整理一个完整的笔记如下,希望能帮助像我这样入门的新人,快速理解逻辑回归算法原理和逻辑回归实现代码。
目录
一、什么是逻辑回归模型
1.1 什么是逻辑回归模型
逻辑回归模型(Logistic Regression)包含了二元逻辑回归和多元逻辑回归,二元逻辑回归用来解决二分类问题,多元逻辑回归用来解决多分类问题。多元逻辑回归属于二元逻辑回归的拓展,但二元逻辑回归用得最多,学习应先从二元逻辑回归开始。多元逻辑回归在需要时可以选择性学习。一般所说的逻辑回归都是指二元逻辑回归,本文的逻辑回归也是指二元逻辑回归。
1.2 线性回归与逻辑回归的区别与关系
线性回归是用做数值预测的,属于回归模型。而逻辑回归是用来做类别预测的,属于模式识别模型。它们的共同之处是,X和y都是线性关系。可以说,逻辑回归是“用于做类别预测”的线性回归。
1.3 逻辑回归公式
逻辑回归的公式包括三部分:
(1) 逻辑回归模型公式:逻辑回归模型公式是模型用来计算模型预测结果的公式
(2) 逻辑回归损失函数公式:逻辑回归损失函数公式是用来训练模型的评估指标
(3) 逻辑回归梯度公式:逻辑回归梯度公式是训练模型时用来调整模型参数的公式
下面详细梳理逻辑回归模型原理,并理解上面三条公式,也就基本弄清楚逻辑回归算法了。
二、逻辑回归模型原理
2.1 逻辑回归模型算法原理
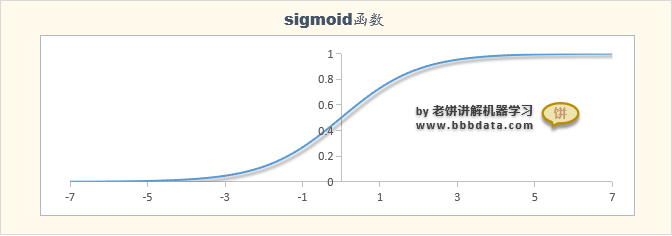
线性回归拟合的是数值,并不符合二分类问题预测类别的需求,但数值与类别也是有关联的,例如,天色越黑,下雨概率就越大,即值越大,属于某类别的概率也越大,值与概率之间可以互转。 在数学里通常用函数Sigmoid函数将数值转化为概率:
,sigmoid函数的输出区间为(0,1),它与概率的范围是一致的,
2.2 逻辑回归模型公式
根据逻辑回归模型原理,所以,很自然地,逻辑回归模型公式为:
三、逻辑回归损失函数与逻辑回归训练
3.1 逻辑回归损失函数
逻辑回归的损失函数为交叉熵损失函数:
逻辑回归模型中的w,b参数需要通过数据训练来得到,训练的标准就是使以上的交叉熵损失函数值最小,它的意义是模型预测正确概率最大化,可以通过最大似然法推导出来
具体可参考文章《逻辑回归损失函数推导过程》
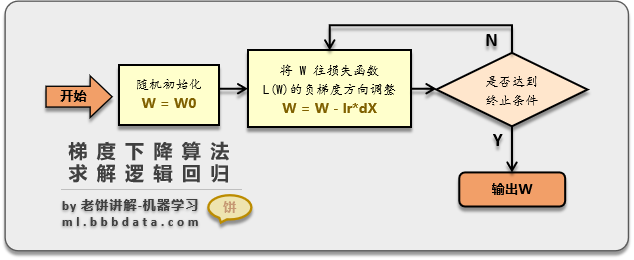
3.2 逻辑回归模型训练
训练逻辑回归模型可以使用梯度下降法,梯度下降法通过将损失函数每次往负梯度方向调整来找到局部最优解。梯度下降法训练逻辑回归算法流程图如下:
3.3 逻辑回归梯度公式
逻辑回归模型训练过程需要使用到逻辑回归损失函数的梯度公式,逻辑回归梯度公式如下:
可以结合下面的代码来理解公式
四、逻辑回归实现python代码
4.1 python实现逻辑回归(调用sklearn)
python实现逻辑回归一般通过sklearn包来完成,具体示例代码如下:
""" 本代码展示在python中调用sklearn来训练逻辑回归模型 本代码来自《老饼讲解-机器学习》www.bbbdata.com """ from sklearn.datasets import load_breast_cancer from sklearn.linear_model import LogisticRegression import numpy as np #----数据加载------ data = load_breast_cancer() # 加载breast_cancer数据 X = data.data[:,4:8] # 作为示例,只使用4个变量来建模 y = data.target # 类别标签 #-----训练模型-------------------- clf = LogisticRegression(random_state=0) # 初始化逻辑回归模型 clf.fit(X,y) # 训练逻辑回归模型 #------打印结果------------------------ print("模型参数:"+str(clf.coef_)) # 打印模型系数 print("模型阈值:"+str(clf.intercept_)) # 打印模型阈值运行后输出结果如下:
模型参数:[[-0.53024026 -3.48636783 -6.89132654 -4.37965412]]
模型阈值:[1.80112869]4.2 python实现逻辑回归(自己实现)
也可以自己通过算法原理来实现逻辑回归的训练,结合梯度下降算法与逻辑回归梯度公式就可以,具体示例代码如下:
""" 本代码展示梯度下降求解逻辑回归的python代码实现 本代码来自《老饼讲解-机器学习》www.bbbdata.com """ from sklearn.datasets import load_breast_cancer import numpy as np #----数据加载------ data = load_breast_cancer() # 加载breast_cancer数据 X = data.data[:,4:8] # 作为示例,只使用4个变量来建模 y = data.target # 类别标签 xt = np.insert(X, X.shape[1], 1, axis=1) # 给X增加一列,作为阈值 #-----梯度下降求解w--------------- np.random.seed(888) # 设定随机种子,以确保每次程序结果一次 w = np.random.rand(xt.shape[1]) # 初始化权重 for i in range(10000): # 逐步训练权重 p = 1/(1+np.exp(-xt@w)) # 计算p w = w - 0.01*(xt.T@(p-y)) # 往负梯度方向更新w p = 1/(1+np.exp(-xt@w)) # 最终的预测结果 print("参数w:"+str(w)) # 打印参数运行后输出结果如下:
参数w:[ 7.16215375 14.98708501 -16.84689114 -73.92486786 3.38331608]4.3 逻辑回归模型评估
训练完成后,将参数代回到逻辑回归模型,就是最用终来预测所使用的公式:
整理不易,点赞收藏!
相关链接:《sklearn逻辑回归参数详解》