[电路]系列文章目录
1-发出功率和吸收功率关系
2-独立源和受控源
3-基尔霍夫定律
4-两端电路等效变换、电阻串并联
5-电压源、电流源的串联和并联
6-电阻的星形连接和角形连接等效变换(星角变换)
7-实际电源模型和等效变换
8-无源一端口网络输入电阻
9-电路的图及相关概念
10-支路电流法
11-网孔电流法
12-回路电流法
13-结点电压法
一、概述
1 定义
以结点电压为未知量列写电路方程分析电路的方法
2 思路
选结点电压为未知量,则 KVL 自动满足,无需列写 KVL 方程。各支路电流、电压可视为结点电压的线性组合,求出结点电压后,便可方便地得到各支路电压、电流。
3 列写方程说明
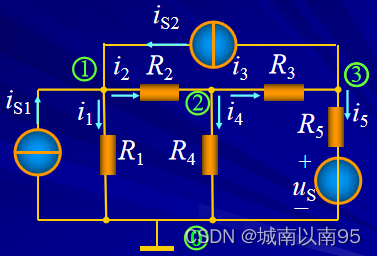
以如下电路为例,对结点电压法需要列写的方程进行分析。
步骤:
- 图中共有 4 个结点,选择结点 0 作为参考结点,其余结点编号为①、②和③,规定结点①、②、③的结点电压分别用 u n 1 、 u n 2 、 u n 3 u_{n1}、u_{n2}、u_{n3} un1、un2、un3 表示。
- 在结点①、②、③的 KCL 方程为:
{ i 1 + i 2 = i S 1 + i S 2 − i 2 + i 3 + i 4 = 0 − i 3 + i 5 = − i S 2 \begin{cases}i_{1}+i_{2}=i_{S1}+i_{S2}\\ -i_{2}+i_{3}+i_{4}=0\\ -i_{3}+i_{5}=-i_{S2}\end{cases} ⎩⎪⎨⎪⎧i1+i2=iS1+iS2−i2+i3+i4=0−i3+i5=−iS2 - 根据各支路的 VCR 及支路电压与结点电压的关系,得到如下方程:
{ u n 1 R 1 + u n 1 − u n 2 R 2 = i S 1 + i S 2 − u n 1 − u n 2 R 2 + u n 2 − u n 3 R 3 + u n 2 R 4 = 0 − u n 2 − u n 3 R 3 + u n 3 − u S R 5 = − i S 2 \begin{cases}\frac {u_{n1}}{R_{1}}+\frac {u_{n1}-u_{n2}}{R_{2}}=i_{S1}+i_{S2}\\ -\frac {u_{n1}-u_{n2}}{R_{2}}+\frac {u_{n2}-u_{n3}}{R_{3}}+\frac {u_{n2}}{R_{4}}=0\\ -\frac {u_{n2}-u_{n3}}{R_{3}}+\frac {u_{n3}-u_{S}}{R_{5}}=-i_{S2}\end{cases} ⎩⎪⎨⎪⎧R1un1+R2un1−un2=iS1+iS2−R2un1−un2+R3un2−un3+R4un2=0−R3un2−un3+R5un3−uS=−iS2 - 经整理,可得到以结点电压为独立变量的方程:
{ ( 1 R 1 + 1 R 2 ) u n 1 − 1 R 2 u n 2 = i S 1 + i S 2 − 1 R 2 u n 1 + ( 1 R 2 + 1 R 3 + 1 R 4 ) u n 2 − 1 R 3 u n 3 = 0 − 1 R 3 u n 2 + ( 1 R 3 + 1 R 5 ) u n 3 = − i S 2 + u S R 5 \begin{cases}(\frac {1}{R_{1}}+\frac {1}{R_{2}})u_{n1} -\frac {1}{R_{2}}u_{n2}=i_{S1}+i_{S2}\\ -\frac {1}{R_{2}}u_{n1}+(\frac {1}{R_{2}}+\frac {1}{R_{3}}+\frac {1}{R_{4}})u_{n2}-\frac {1}{R_{3}}u_{n3}=0\\ -\frac {1}{R_{3}}u_{n2}+(\frac {1}{R_{3}}+\frac {1}{R_{5}})u_{n3}=-i_{S2}+\frac {u_{S}}{R_{5}}\end{cases} ⎩⎪⎨⎪⎧(R11+R21)un1−R21un2=iS1+iS2−R21un1+(R21+R31+R41)un2−R31un3=0−R31un2+(R31+R51)un3=−iS2+R5uS - 令
G
k
=
1
R
k
,
k
=
1
,
2
,
3
,
4
,
5
G_k = \frac {1}{R_{k}},\ k=1,2,3,4,5
Gk=Rk1, k=1,2,3,4,5,上式简记为:
{ G 11 u n 1 + G 12 u n 2 + G 13 u n 3 = i S n 1 G 21 u n 1 + G 22 u n 2 + G 23 u n 3 = i S n 2 G 31 u n 1 + G 32 u n 2 + G 33 u n 3 = i S n 3 \begin{cases}G_{11}u_{n1}+G_{12}u_{n2}+G_{13}u_{n3}=i_{Sn1}\\ G_{21}u_{n1}+G_{22}u_{n2}+G_{23}u_{n3}=i_{Sn2}\\ G_{31}u_{n1}+G_{32}u_{n2}+G_{33}u_{n3}=i_{Sn3}\end{cases} ⎩⎪⎨⎪⎧G11un1+G12un2+G13un3=iSn1G21un1+G22un2+G23un3=iSn2G31un1+G32un2+G33un3=iSn3
式中,用自导、互导和电流源电流代数和的形式进行表示。
自导: 电导符号具有相同双下标,如 G 11 G_{11} G11。自导总为正,等于接在该结点上所有支路的电导之和。
互导: 电导符号具有不同的双下标,如 G 12 G_{12} G12。互导总为负,等于连接于两结点间支路电导的负值。
电流源电流代数和: 等于流向结点的电流源的代数和,流入结点者前面取正号,流出结点者前面取负号。
4 公式推广
对于具有 n 个结点的电路,结点电压法标准形式的方程如下:
{
G
11
u
n
1
+
G
12
u
n
2
+
⋯
+
G
1
,
n
−
1
u
n
,
n
−
1
=
i
S
n
1
G
21
u
n
1
+
G
22
u
n
2
+
⋯
+
G
2
,
n
−
1
u
n
,
n
−
1
=
i
S
n
2
⋯
G
n
−
1
,
1
u
n
1
+
G
n
−
1
,
2
u
n
2
+
⋯
+
G
n
−
1
,
,
n
−
1
u
n
,
n
−
1
=
i
S
n
,
n
−
1
\begin{cases}G_{11}u_{n1}+G_{12}u_{n2}+\cdots +G_{1,n-1}u_{n,n-1}=i_{Sn1}\\ G_{21}u_{n1}+G_{22}u_{n2}+\cdots +G_{2,n-1}u_{n,n-1}=i_{Sn2}\\ \cdots \\ G_{n-1,1}u_{n1}+G_{n-1,2}u_{n2}+\cdots +G_{n-1,,n-1}u_{n,n-1}=i_{Sn,n-1}\end{cases}
⎩⎪⎪⎪⎨⎪⎪⎪⎧G11un1+G12un2+⋯+G1,n−1un,n−1=iSn1G21un1+G22un2+⋯+G2,n−1un,n−1=iSn2⋯Gn−1,1un1+Gn−1,2un2+⋯+Gn−1,,n−1un,n−1=iSn,n−1
二、使用步骤
- 选定参考结点,标定 n-1 个独立结点;
- 对 n-1 个独立结点,以结点电压为未知量,列写其 KCL 方程;
- 求解上述方程,得到 n-1 个结点电压;
- 通过结点电压求各支路电流;
- 其它分析。
注意:
- 适用于结点较少的电路;
- 任意选择参考点:其它结点与参考点的电位差即为结点电压,方向为从独立结点指向参考结点。
更多内容关注微信公众号:城南以南95
愿余生,不负岁月,不负自己。 喜欢就点个赞吧