0基础跟德姆（dom）一起学AI 自然语言处理16-输入部分实现

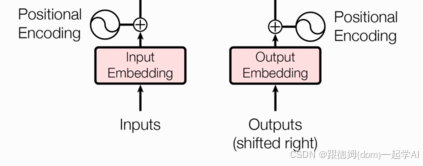
1 输入部分介绍

输入部分包含:

源文本嵌入层及其位置编码器
目标文本嵌入层及其位置编码器

2 文本嵌入层的作用

无论是源文本嵌入还是目标文本嵌入，都是为了将文本中词汇的数字表示转变为向量表示, 希望在这样的高维空间捕捉词汇间的关系.
文本嵌入层的代码分析:

# 导入必备的工具包
import torch

# 预定义的网络层torch.nn, 工具开发者已经帮助我们开发好的一些常用层, 
# 比如，卷积层, lstm层, embedding层等, 不需要我们再重新造轮子.
import torch.nn as nn

# 数学计算工具包
import math

# torch中变量封装函数Variable.
from torch.autograd import Variable

# Embeddings类 实现思路分析
# 1 init函数 (self, d_model, vocab)
    # 设置类属性 定义词嵌入层 self.lut层
# 2 forward(x)函数
    # self.lut(x) * math.sqrt(self.d_model)
class Embeddings(nn.Module):
    def __init__(self, d_model, vocab):
        # 参数d_model 每个词汇的特征尺寸 词嵌入维度
        # 参数vocab   词汇表大小
        super(Embeddings, self).__init__()
        self.d_model = d_model
        self.vocab = vocab

        # 定义词嵌入层
        self.lut = nn.Embedding(self.vocab, self.d_model)

    def forward(self, x):
        # 将x传给self.lut并与根号下self.d_model相乘作为结果返回
        # x经过词嵌入后 增大x的值, 词嵌入后的embedding_vector+位置编码信息,值量纲差差不多
        return self.lut(x) * math.sqrt(self.d_model)

nn.Embedding演示:

>>> embedding = nn.Embedding(10, 3)
>>> input = torch.LongTensor([[1,2,4,5],[4,3,2,9]])
>>> embedding(input)
tensor([[[-0.0251, -1.6902,  0.7172],
         [-0.6431,  0.0748,  0.6969],
         [ 1.4970,  1.3448, -0.9685],
         [-0.3677, -2.7265, -0.1685]],

        [[ 1.4970,  1.3448, -0.9685],
         [ 0.4362, -0.4004,  0.9400],
         [-0.6431,  0.0748,  0.6969],
         [ 0.9124, -2.3616,  1.1151]]])


>>> embedding = nn.Embedding(10, 3, padding_idx=0)
>>> input = torch.LongTensor([[0,2,0,5]])
>>> embedding(input)
tensor([[[ 0.0000,  0.0000,  0.0000],
         [ 0.1535, -2.0309,  0.9315],
         [ 0.0000,  0.0000,  0.0000],
         [-0.1655,  0.9897,  0.0635]]])

调用

def dm_test_Embeddings():
    d_model = 512   # 词嵌入维度是512维
    vocab = 1000    # 词表大小是1000
    # 实例化词嵌入层
    my_embeddings = Embeddings(d_model, vocab)
    x = Variable(torch.LongTensor([[100,2,421,508],[491,998,1,221]]))
    embed = my_embeddings(x)
    print('embed.shape', embed.shape, '\nembed--->\n',embed)

输出效果

embed.shape torch.Size([2, 4, 512]) 
embed--->
 tensor([[[-19.0429, -44.2167,   2.6662,  ..., -21.1199, -36.5275, -15.6872],
         [-25.4621,  25.6046, -45.5382,  ...,  43.7159,   0.9437,  -3.1733],
         [-15.7487,   8.1787, -20.6409,  ...,  -8.7201,  -3.2585, -22.1298],
         [ 21.5044,   2.0660,  -1.4059,  ...,  -6.3673,   3.4387, -22.4600]],

        [[ 15.7010,   2.6187,  14.1192,  ..., -19.1751,  10.5954,   9.1155],
         [-21.5745,   9.6403,  17.9778,  ...,   2.3668,  30.1526, -30.3724],
         [-17.6655,  33.6687,  19.3059,  ..., -10.6276,  -0.8653,  10.0715],
         [ 12.9400, -23.6355,  -2.4750,  ...,  19.1028,   6.6492, -45.1315]]],
       grad_fn=<MulBackward0>)

3 位置编码器的作用

因为在Transformer的编码器结构中, 并没有针对词汇位置信息的处理，因此需要在Embedding层后加入位置编码器，将词汇位置不同可能会产生不同语义的信息加入到词嵌入张量中, 以弥补位置信息的缺失.

3.1 位置编码器的代码分析

# 位置编码器类PositionalEncoding 实现思路分析
# 1 init函数  (self, d_model, dropout, max_len=5000)
#   super()函数 定义层self.dropout
#   定义位置编码矩阵pe  定义位置列-矩阵position 定义变化矩阵div_term
#   套公式div_term = torch.exp(torch.arange(0, d_model, 2) * -(math.log(10000.0)/d_model))
#   位置列-矩阵 * 变化矩阵 阿达码积my_matmulres
#   给pe矩阵偶数列奇数列赋值 pe[:, 0::2] pe[:, 1::2]
#   pe矩阵注册到模型缓冲区 pe.unsqueeze(0)三维 self.register_buffer('pe', pe)
# 2 forward(self, x) 返回self.dropout(x)
#   给x数据添加位置特征信息 x = x + Variable( self.pe[:,:x.size()[1]], requires_grad=False)

class PositionalEncoding(nn.Module):
    def __init__(self, d_model, dropout, max_len=5000):
        # 参数d_model 词嵌入维度 eg: 512个特征
        # 参数max_len 单词token个数 eg: 60个单词
        super(PositionalEncoding, self).__init__()

        # 定义dropout层
        self.dropout = nn.Dropout(p=dropout)

        # 思路：位置编码矩阵 + 特征矩阵 相当于给特征增加了位置信息
        # 定义位置编码矩阵PE eg pe[60, 512], 位置编码矩阵和特征矩阵形状是一样的
        pe = torch.zeros(max_len, d_model)

        # 定义位置列-矩阵position  数据形状[max_len,1] eg: [0,1,2,3,4...60]^T
        position = torch.arange(0, max_len).unsqueeze(1)
        # print('position--->', position.shape, position)

        # 定义变化矩阵div_term [1,256]
        # torch.arange(start=1, end=512, 2)结果并不包含end。在start和end之间做一个等差数组 [0, 2, 4, 6 ... 510]
        div_term = torch.exp(torch.arange(0, d_model, 2) * -(math.log(10000.0) / d_model))

        # 位置列-矩阵 @ 变化矩阵 做矩阵运算 [60*1]@ [1*256] ==> 60 *256
        # 矩阵相乘也就是行列对应位置相乘再相加，其含义，给每一个列属性（列特征）增加位置编码信息
        my_matmulres = position * div_term
        # print('my_matmulres--->', my_matmulres.shape, my_matmulres)

        # 给位置编码矩阵奇数列，赋值sin曲线特征
        pe[:, 0::2] = torch.sin(my_matmulres)
        # 给位置编码矩阵偶数列，赋值cos曲线特征
        pe[:, 1::2] = torch.cos(my_matmulres)

        # 形状变化 [60,512]-->[1,60,512]
        pe = pe.unsqueeze(0)

        # 把pe位置编码矩阵 注册成模型的持久缓冲区buffer; 模型保存再加载时，可以根模型参数一样，一同被加载
        # 什么是buffer: 对模型效果有帮助的，但是却不是模型结构中超参数或者参数，不参与模型训练
        self.register_buffer('pe', pe)

    def forward(self, x):
        # 注意：输入的x形状2*4*512  pe是1*60*512 形状 如何进行相加
        # 只需按照x的单词个数 给特征增加位置信息
        x = x + Variable( self.pe[:,:x.size()[1]], requires_grad=False)
        return self.dropout(x)

nn.Dropout演示

>>> m = nn.Dropout(p=0.2)
>>> input = torch.randn(4, 5)
>>> output = m(input)
>>> output
Variable containing:
 0.0000 -0.5856 -1.4094  0.0000 -1.0290
 2.0591 -1.3400 -1.7247 -0.9885  0.1286
 0.5099  1.3715  0.0000  2.2079 -0.5497
-0.0000 -0.7839 -1.2434 -0.1222  1.2815
[torch.FloatTensor of size 4x5]

torch.unsqueeze演示

>>> x = torch.tensor([1, 2, 3, 4])
>>> torch.unsqueeze(x, 0)
tensor([[ 1,  2,  3,  4]])
>>> torch.unsqueeze(x, 1)
tensor([[ 1],
        [ 2],
        [ 3],
        [ 4]])

调用

def dm_test_PositionalEncoding():

    d_model = 512  # 词嵌入维度是512维
    vocab = 1000  # 词表大小是1000

    # 1 实例化词嵌入层
    my_embeddings = Embeddings(d_model, vocab)

    # 2 让数据经过词嵌入层 [2,4] --->[2,4,512]
    x = Variable(torch.LongTensor([[100, 2, 421, 508], [491, 998, 1, 221]]))
    embed = my_embeddings(x)
    # print('embed--->', embed.shape)

    # 3 创建pe位置矩阵 生成位置特征数据[1,60,512]
    my_pe = PositionalEncoding(d_model=d_model, dropout=0.1, max_len=60)

    # 4 给词嵌入数据embed 添加位置特征 [2,4,512] ---> [2,4,512]
    pe_result = my_pe(embed)
    print('pe_result.shape--->', pe_result.shape)
    print('pe_result--->', pe_result)

输出效果

pe_result.shape---> torch.Size([2, 4, 512])
pe_result---> tensor([[[ -6.3490, -19.3785,  -2.8700,  ..., -23.4560, -31.7405,   9.0657],
         [-27.7453,  19.5398,  62.4924,  ...,  -7.7443,  12.3955, -29.1615],
         [ 80.8307,   4.9565,  -0.7523,  ...,   8.2715,  26.7639,  -6.9124],
         [ 13.3252, -21.8653,   0.0000,  ...,  -8.4563,  17.7678,   9.6917]],

        [[  5.2631,  22.0867,  15.3600,  ...,  80.5963,   2.4491, -36.0901],
         [-19.0809,  67.3568,  10.3016,  ...,  -5.6103, -14.2998, -51.2010],
         [-31.1153,  44.8199,  -6.9740,  ...,  39.6247,  33.6903,  18.5471],
         [ 13.7074,  26.4221, -27.3353,  ...,  24.1987,  29.1897, -20.5858]]],
       grad_fn=<MulBackward0>)

3.2 绘制词汇向量中特征的分布曲线

import matplotlib.pyplot as plt
import numpy as np

# 绘制PE位置特征sin-cos曲线
def dm_draw_PE_feature():

    # 1 创建pe位置矩阵[1,5000,20]，每一列数值信息：奇数列sin曲线 偶数列cos曲线
    my_pe = PositionalEncoding(d_model=20, dropout=0)
    print('my_positionalencoding.shape--->', my_pe.pe.shape)

    # 2 创建数据x[1,100,20], 给数据x添加位置特征  [1,100,20] ---> [1,100,20]
    y = my_pe(Variable(torch.zeros(1, 100, 20)))
    print('y--->', y.shape)

    # 3 画图 绘制pe位置矩阵的第4-7列特征曲线
    plt.figure(figsize=(20, 20))
    # 第0个句子的，所有单词的，绘制4到8维度的特征 看看sin-cos曲线变化
    plt.plot(np.arange(100), y[0, :, 4:8].numpy())
    plt.legend(["dim %d" %p for p in [4,5,6,7]])
    plt.show()

    # print('直接查看pe数据形状--->', my_pe.pe.shape) # [1,5000,20]
    # 直接绘制pe数据也是ok
    # plt.figure(figsize=(20, 20))
    # # 第0个句子的，所有单词的，绘制4到8维度的特征 看看sin-cos曲线变化
    # plt.plot(np.arange(100), my_pe.pe[0,0:100, 4:8])
    # plt.legend(["dim %d" %p for p in [4,5,6,7]])
    # plt.show()

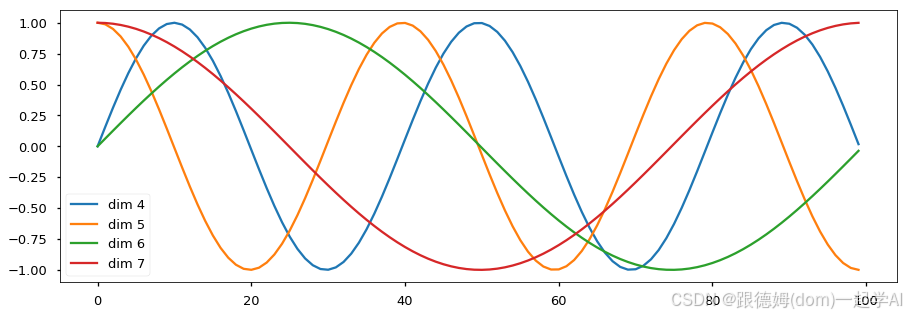
输出效果:

效果分析
每条颜色的曲线代表某一个词汇中的特征在不同位置的含义
保证同一词汇随着所在位置不同它对应位置嵌入向量会发生变化
正弦波和余弦波的值域范围都是1到-1这又很好的控制了嵌入数值的大小, 有助于梯度的快速计算

0基础跟德姆（dom）一起学AI 自然语言处理16-输入部分实现

1 输入部分介绍

2 文本嵌入层的作用

3 位置编码器的作用

3.1 位置编码器的代码分析

3.2 绘制词汇向量中特征的分布曲线

悦读